偏微分方程算法之椭圆型方程差分格式编程示例
目录
一、示例1-五点菱形格式
1.1 C++代码
1.2 计算结果
二、示例2-九点紧差分格式
2.1 C++代码
2.2 计算结果
三、示例3-二阶混合边值
3.1 C++代码
3.2 计算结果
本专栏对椭圆型偏微分方程的三种主要差分方法进行了介绍,并给出相应格式的理论推导过程。为加深对差分格式的理解,分别对三种方法进行C++编程示例。
一、示例1-五点菱形格式
已知精确解为。分别取两种剖分数:m=20,n=30和m=40,n=60,输出10个节点
和
处的数值解,并给出误差。要求在各个节点处最大误差的迭代误差限为
。
1.1 C++代码
#include <cmath>
#include <stdlib.h>
#include <stdio.h>int main(int argc, char* argv[])
{int m,n,i,j,k,num;double xa,xb,ya,yb,dx,dy,alpha,beta,gamma,err,maxerr;double *x,*y,**u,**temp;double leftboundary(double y);double rightboundary(double y);double bottomboundary(double x);double topboundary(double x);double f(double x, double y);double exact(double x, double y);xa=1.0;xb=2.0;ya=0.0;yb=3.0;m=20;n=30;printf("m=%d,n=%d.\n",m,n);dx=(xb-xa)/m;dy=(yb-ya)/n;beta=1.0/(dx*dx);gamma=1.0/(dy*dy);alpha=2.0*(beta+gamma);x=(double*)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i]=xa+i*dx;y=(double*)malloc(sizeof(double)*(n+1));for(j=0;j<=n;j++)y[j]=ya+j*dy;u=(double**)malloc(sizeof(double*)*(m+1));temp=(double**)malloc(sizeof(double*)*(m+1));for(i=0;i<=m;i++){u[i]=(double*)malloc(sizeof(double)*(n+1));temp[i]=(double*)malloc(sizeof(double)*(n+1));}for(j=0;j<=n;j++){u[0][j]=leftboundary(y[j]);u[m][j]=rightboundary(y[j]);}for(i=1;i<m;i++){u[i][0]=bottomboundary(x[i]);u[i][n]=topboundary(x[i]);}for(i=1;i<m;i++){for(j=1;j<n;j++)u[i][j]=0.0;}for(i=0;i<=m;i++){for(j=0;j<=n;j++)temp[i][j]=u[i][j];}k=0;do{maxerr=0.0;for(i=1;i<m;i++){for(j=1;j<n;j++){temp[i][j]=(f(x[i],y[j])+beta*(u[i-1][j]+temp[i+1][j])+gamma*(u[i][j-1]+temp[i][j+1]))/alpha;err=fabs(temp[i][j]-u[i][j]);if(err>maxerr)maxerr=err;u[i][j]=temp[i][j];}}k=k+1;}while(maxerr>0.5*1e-10);printf("k=%d.\n",k);k=n/6;num=m/4;for(j=k;j<n;j=j+k){printf("(1.25,%.3f), y=%f, err=%.4e.\n",y[j],u[num][j],fabs(exact(x[num],y[j])-u[num][j]));}num=3*m/4;for(j=k;j<n;j=j+k){printf("(1.75,%.3f), y=%f, err=%.4e.\n",y[j],u[num][j],fabs(exact(x[num],y[j])-u[num][j]));}for(i=0;i<=m;i++){free(u[i]);free(temp[i]);}free(x);free(y);return 0;
}double leftboundary(double y)
{return log(1.0+2*y*y);
}
double rightboundary(double y)
{return log(4.0+2*y*y);
}
double bottomboundary(double x)
{return 2*log(x);
}
double topboundary(double x)
{return log(18.0+x*x);
}
double f(double x, double y)
{double temp1,temp2,z;temp1=x*x; temp2=y*y;z=temp1+2*temp2;return (4*temp2-2*temp1)/(z*z);
}
double exact(double x, double y)
{return log(x*x+2*y*y);
}1.2 计算结果
当m=20,n=30时,计算结果为:
m=20,n=30.
k=959.
(1.25,0.500), y=0.724037, err=1.1827e-04.
(1.25,1.000), y=1.270654, err=1.9108e-04.
(1.25,1.500), y=1.802202, err=7.9937e-05.
(1.25,2.000), y=2.257872, err=2.3280e-05.
(1.25,2.500), y=2.643516, err=4.1352e-06.
(1.75,0.500), y=1.270488, err=2.5584e-05.
(1.75,1.000), y=1.621992, err=1.3181e-04.
(1.75,1.500), y=2.023279, err=7.7668e-05.
(1.75,2.000), y=2.403589, err=2.7872e-05.
(1.75,2.500), y=2.744871, err=6.9853e-06.当m=40,n=60时,计算结果为:
m=40,n=60.
k=3582.
(1.25,0.500), y=0.723948, err=2.9304e-05.
(1.25,1.000), y=1.270510, err=4.7781e-05.
(1.25,1.500), y=1.802142, err=1.9972e-05.
(1.25,2.000), y=2.257855, err=5.8033e-06.
(1.25,2.500), y=2.643513, err=1.0237e-06.
(1.75,0.500), y=1.270469, err=6.1963e-06.
(1.75,1.000), y=1.621893, err=3.2942e-05.
(1.75,1.500), y=2.023221, err=1.9426e-05.
(1.75,2.000), y=2.403568, err=6.9568e-06.
(1.75,2.500), y=2.744866, err=1.7374e-06.二、示例2-九点紧差分格式
已知精确解为。分别取两种剖分数:m=20,n=30和m=40,n=60,输出10个节点
和
处的数值解,并给出误差。要求在各个节点处最大误差的迭代误差限为
。
2.1 C++代码
#include <cmath>
#include <stdlib.h>
#include <stdio.h>int main(int argc, char*argv[])
{int m,n,i,j,k,num;double xa,xb,ya,yb,dx,dy,alpha,beta,gamma,err,maxerr;double *x,*y,**u,**g,**temp,kexi,eta1,eta2;double leftboundary(double y);double rightboundary(double y);double bottomboundary(double x);double topboundary(double x);double f(double x, double y);double **Gij(double *x, double *y, int m, int n);double exact(double x, double y);xa=1.0;xb=2.0;ya=0.0;yb=3.0;m=20;n=30;printf("m=%d,n=%d.\n",m,n);dx=(xb-xa)/m;dy=(yb-ya)/n;beta=1.0/(dx*dx);gamma=1.0/(dy*dy);kexi=beta+gamma;eta1=10*beta-2*gamma;eta2=10*gamma-2*beta;x=(double*)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i]=xa+i*dx;y=(double*)malloc(sizeof(double)*(n+1));for(j=0;j<=n;j++)y[j]=ya+j*dy;u=(double**)malloc(sizeof(double*)*(m+1));temp=(double**)malloc(sizeof(double*)*(m+1));for(i=0;i<=m;i++){u[i]=(double*)malloc(sizeof(double)*(n+1));temp[i]=(double*)malloc(sizeof(double)*(n+1));}for(j=0;j<=n;j++){u[0][j]=leftboundary(y[j]);u[m][j]=rightboundary(y[j]);}for(i=1;i<m;i++){u[i][0]=bottomboundary(x[i]);u[i][n]=topboundary(x[i]);}for(i=1;i<m;i++){for(j=1;j<n;j++)u[i][j]=0.0;}g=Gij(x,y,m,n);for(i=0;i<=m;i++){for(j=0;j<=n;j++)temp[i][j]=u[i][j];}k=0;do{maxerr=0.0;for(i=1;i<m;i++){for(j=1;j<n;j++){temp[i][j]=(g[i][j]-kexi*(u[i-1][j-1]+temp[i-1][j+1]+u[i+1][j-1]+temp[i+1][j+1])-eta1*(u[i-1][j]+temp[i+1][j])-eta2*(u[i][j-1]+temp[i][j+1]))/(-20*kexi);err=fabs(temp[i][j]-u[i][j]);if(err>maxerr)maxerr=err;u[i][j]=temp[i][j];}}k=k+1;}while(maxerr>0.5*1e-10);printf("k=%d.\n",k);k=n/6;num=m/4;for(j=k;j<n;j=j+k){printf("(1.25,%.3f), y=%f, err=%.4e.\n",y[j],u[num][j],fabs(exact(x[num],y[j])-u[num][j]));}num=3*m/4;for(j=k;j<n;j=j+k){printf("(1.75,%.3f), y=%f, err=%.4e.\n",y[j],u[num][j],fabs(exact(x[num],y[j])-u[num][j]));}for(i=0;i<=m;i++){free(u[i]);free(temp[i]);}free(u);free(temp);free(x);free(y);return 0;
}double leftboundary(double y)
{return log(1.0+2*y*y);
}
double rightboundary(double y)
{return log(4.0+2*y*y);
}
double bottomboundary(double x)
{return 2*log(x);
}
double topboundary(double x)
{return log(18+x*x);
}
double f(double x, double y)
{double temp1, temp2, z;temp1=x*x;temp2=y*y;z=temp1+2*temp2;return (4*temp2-2*temp1)/(z*z);
}
double exact(double x, double y)
{return log(x*x+2*y*y);
}
double **Gij(double *x, double *y, int m, int n)
{int i,j;double temp1,temp2,temp3,**ans;ans=(double**)malloc(sizeof(double*)*(m+1));for(i=0;i<=m;i++)ans[i]=(double*)malloc(sizeof(double)*(n+1));for(i=0;i<=m;i++){for(j=0;j<=n;j++)ans[i][j]=0.0;}for(i=1;i<m;i++){for(j=1;j<n;j++){temp1=f(x[i-1],y[j-1])+10*f(x[i],y[j-1])+f(x[i+1],y[j-1]);temp2=f(x[i-1],y[j])+10*f(x[i],y[j])+f(x[i+1],y[j]);temp3=f(x[i-1],y[j+1])+10*f(x[i],y[j+1])+f(x[i+1],y[j+1]);ans[i][j]=-(temp1+temp3+10*temp2)/12.0;}}return ans;
}2.2 计算结果
当m=20,n=30时,计算结果为:
m=20,n=30.
k=805.
(1.25,0.500), y=0.723921, err=2.5068e-06.
(1.25,1.000), y=1.270463, err=4.0234e-07.
(1.25,1.500), y=1.802122, err=8.8970e-08.
(1.25,2.000), y=2.257849, err=6.0205e-08.
(1.25,2.500), y=2.643512, err=2.1371e-08.
(1.75,0.500), y=1.270463, err=8.8774e-07.
(1.75,1.000), y=1.621861, err=5.0648e-07.
(1.75,1.500), y=2.023202, err=1.3736e-10.
(1.75,2.000), y=2.403561, err=4.9714e-08.
(1.75,2.500), y=2.744864, err=2.2523e-08.当m=40,n=60时,计算结果为:
m=40,n=60.
k=3012.
(1.25,0.500), y=0.723919, err=1.5248e-07.
(1.25,1.000), y=1.270463, err=2.0549e-08.
(1.25,1.500), y=1.802122, err=1.0963e-08.
(1.25,2.000), y=2.257849, err=8.4329e-09.
(1.25,2.500), y=2.643512, err=4.0188e-09.
(1.75,0.500), y=1.270463, err=5.2372e-08.
(1.75,1.000), y=1.621860, err=2.7195e-08.
(1.75,1.500), y=2.023202, err=5.0463e-09.
(1.75,2.000), y=2.403561, err=7.4797e-09.
(1.75,2.500), y=2.744864, err=3.9218e-09.三、示例3-二阶混合边值
已知精确解为。分别取两种剖分数:m=20,n=30和m=40,n=60,输出10个节点
和
处的数值解,并给出误差。要求在各个节点处最大误差的迭代误差限为
。
3.1 C++代码
#include <cmath>
#include <stdlib.h>
#include <stdio.h>int main(int argc, char*argv[])
{int m, n, i, j, k, num;double xa, xb, ya, yb, dx, dy, alpha, beta, gamma, maxerr;double *x, *y, **u, **v, **lambda, kexi, eta, *d, temp;double f(double x, double y);double lambda_function(double x, double y);double phi1(double y);double phi2(double y);double psi1(double x);double psi2(double x);double exact(double x, double y);xa=1.0;xb=2.0;ya=0.0;yb=3.0;m=20;n=30;printf("m=%d, n=%d\n", m, n);dx=(xb-xa)/m;dy=(yb-ya)/n;beta=1.0/(dx*dx);gamma=1.0/(dy*dy);alpha=2*(beta+gamma);kexi=2.0/dx;eta=2.0/dy;x=(double*)malloc(sizeof(double)*(m+1));for(i=0;i<=m;i++)x[i]=xa+i*dx;y=(double*)malloc(sizeof(double)*(n+1));for(j=0;j<=n;j++)y[j]=ya+j*dy;u=(double**)malloc(sizeof(double*)*(m+1));v=(double**)malloc(sizeof(double*)*(m+1));lambda=(double**)malloc(sizeof(double*)*(m+1));for(i=0;i<=m;i++){u[i]=(double*)malloc(sizeof(double)*(n+1));v[i]=(double*)malloc(sizeof(double)*(n+1));lambda[i]=(double*)malloc(sizeof(double)*(n+1));}for(i=0;i<=m;i++){for(j=0;j<=n;j++){u[i][j]=0.0;v[i][j]=0.0;lambda[i][j]=lambda_function(x[i], y[j]);}}d=(double*)malloc(sizeof(double)*(m+1));k=0;do{maxerr=0.0;for(i=0;i<=m;i++)d[i]=f(x[i],y[0])-eta*psi1(x[i]);d[0]=d[0]-kexi*phi1(y[0]);d[m]=d[m]+kexi*phi2(y[0]);v[0][0]=(d[0]+2*gamma*u[0][1]+2*beta*u[1][0])/(alpha+(kexi+eta)*lambda[0][0]);for(i=1;i<m;i++)v[i][0]=(d[i]+2*gamma*u[i][1]+beta*(v[i-1][0]+u[i+1][0]))/(alpha+eta*lambda[i][0]);v[m][0]=(d[m]+2*gamma*u[m][1]+2*beta*v[m-1][0])/(alpha+(kexi+eta)*lambda[m][0]);for(j=1;j<n;j++){for(i=0;i<=m;i++)d[i]=f(x[i],y[j]);d[0]=d[0]-kexi*phi1(y[j]);d[m]=d[m]+kexi*phi2(y[j]);v[0][j]=(d[0]+gamma*(u[0][j+1]+v[0][j-1])+2*beta*u[1][j])/(alpha+kexi*lambda[0][j]);for(i=1;i<m;i++)v[i][j]=(d[i]+gamma*(v[i][j-1]+u[i][j+1])+beta*(v[i-1][j]+u[i+1][j]))/alpha;v[m][j]=(d[m]+gamma*(v[m][j-1]+u[m][j+1])+2*beta*v[m-1][j])/(alpha+kexi*lambda[m][j]);}for(i=0;i<=m;i++)d[i]=f(x[i],y[n])+eta*psi2(x[i]);d[0]=d[0]-kexi*phi1(y[n]);d[m]=d[m]+kexi*phi2(y[n]);v[0][n]=(d[0]+2*beta*u[1][n]+2*gamma*v[0][n-1])/(alpha+(kexi+eta)*lambda[0][n]);for(i=1;i<m;i++)v[i][n]=(d[i]+beta*(v[i-1][n]+u[i+1][n])+2*gamma*v[i][n-1])/(alpha+eta*lambda[i][n]);v[m][n]=(d[m]+2*beta*v[m-1][n]+2*gamma*v[m][n-1])/(alpha+(kexi+eta)*lambda[m][n]);for(i=0;i<=m;i++){for(j=0;j<=n;j++){temp=fabs(u[i][j]-v[i][j]);if(temp>maxerr)maxerr=temp;u[i][j]=v[i][j];}}k=k+1;}while((maxerr>0.5*1e-10)&&(k<=1e+8));printf("k=%d\n", k);k=n/6;num=m/4;for(j=k;j<n;j=j+k){printf("(1.25,%.3f), y=%f, err=%.4e.\n",y[j],u[num][j],fabs(exact(x[num],y[j])-u[num][j]));}num=3*m/4;for(j=k;j<n;j=j+k){printf("(1.75,%.3f), y=%f, err=%.4e.\n",y[j],u[num][j],fabs(exact(x[num],y[j])-u[num][j]));}for(i=0;i<=m;i++){free(u[i]);free(v[i]);free(lambda[i]);}free(u);free(v);free(lambda);free(x);free(y);free(d);return 0;
}double f(double x, double y)
{double temp1, temp2, z;temp1=x*x;temp2=y*y;z=temp1+2*temp2;return (4*temp2-2*temp1)/(z*z);
}
double lambda_function(double x, double y)
{return 1.0;
}
double phi1(double y)
{double z;z=1.0+2*y*y;return 2.0/z-log(z);
}
double phi2(double y)
{double z;z=2+y*y;return 2.0/z+log(2*z);
}
double psi1(double x)
{return -2*log(x);
}
double psi2(double x)
{double z;z=x*x+18.0;return 12.0/z+log(z);
}
double exact(double x, double y)
{return log(x*x+2*y*y);
}
3.2 计算结果
当m=20,n=30时,计算结果为:
m=20, n=30
k=4470
(1.25,0.500), y=0.723996, err=7.7043e-05.
(1.25,1.000), y=1.270860, err=3.9760e-04.
(1.25,1.500), y=1.802391, err=2.6918e-04.
(1.25,2.000), y=2.257989, err=1.3972e-04.
(1.25,2.500), y=2.643565, err=5.3582e-05.
(1.75,0.500), y=1.270387, err=7.5935e-05.
(1.75,1.000), y=1.622151, err=2.9080e-04.
(1.75,1.500), y=2.023479, err=2.7756e-04.
(1.75,2.000), y=2.403726, err=1.6475e-04.
(1.75,2.500), y=2.744937, err=7.3239e-05.当m=40,n=60时,计算结果为:
m=40, n=60
k=16565
(1.25,0.500), y=0.723937, err=1.8621e-05.
(1.25,1.000), y=1.270562, err=9.9132e-05.
(1.25,1.500), y=1.802189, err=6.7202e-05.
(1.25,2.000), y=2.257884, err=3.4879e-05.
(1.25,2.500), y=2.643525, err=1.3353e-05.
(1.75,0.500), y=1.270443, err=1.9346e-05.
(1.75,1.000), y=1.621933, err=7.2431e-05.
(1.75,1.500), y=2.023271, err=6.9315e-05.
(1.75,2.000), y=2.403602, err=4.1144e-05.
(1.75,2.500), y=2.744882, err=1.8266e-05.相关文章:
偏微分方程算法之椭圆型方程差分格式编程示例
目录 一、示例1-五点菱形格式 1.1 C代码 1.2 计算结果 二、示例2-九点紧差分格式 2.1 C代码 2.2 计算结果 三、示例3-二阶混合边值 3.1 C代码 3.2 计算结果 本专栏对椭圆型偏微分方程的三种主要差分方法进行了介绍,并给出相应格式的理论推导过程。为加深对…...

PCIe协议之-TLP路由基础
✨前言: 在PCI Express (PCIe) 技术中,数据包的路由方式对于确保信息能够高效、准确地传送至目标设备至关重要。PCIe定义了几种路由方式,主要有以下几种。 🌟地址路由(Address Based Routing) 这是最基本…...
可以是内联函数(inline)吗?)
inline内联函数-虚函数(virtual)可以是内联函数(inline)吗?
目录标题 inline内联函数特征:使用:编译器对inline函数的处理步骤优点:缺点: 虚函数(virtual)可以是内联函数(inline)吗?特征:使用: inline内联函…...

Spring Boot | Spring Boot 消息管理 ( 消息中间件 ) 、RabbitMQ“消息中间件“
目录: 一、"消息服务" 概述 :1.1 为什么要使用 "消息服务" ( 消息中间件 ) ?① 异步处理② 应用解耦③ 流量削峰④ 分布式事务管理 1.2 常用 "消息中间件" 介绍 :ActiveMQ ( 广泛应用于中小型企业 )RabbitMQ ( 没有特别要求的场景下…...
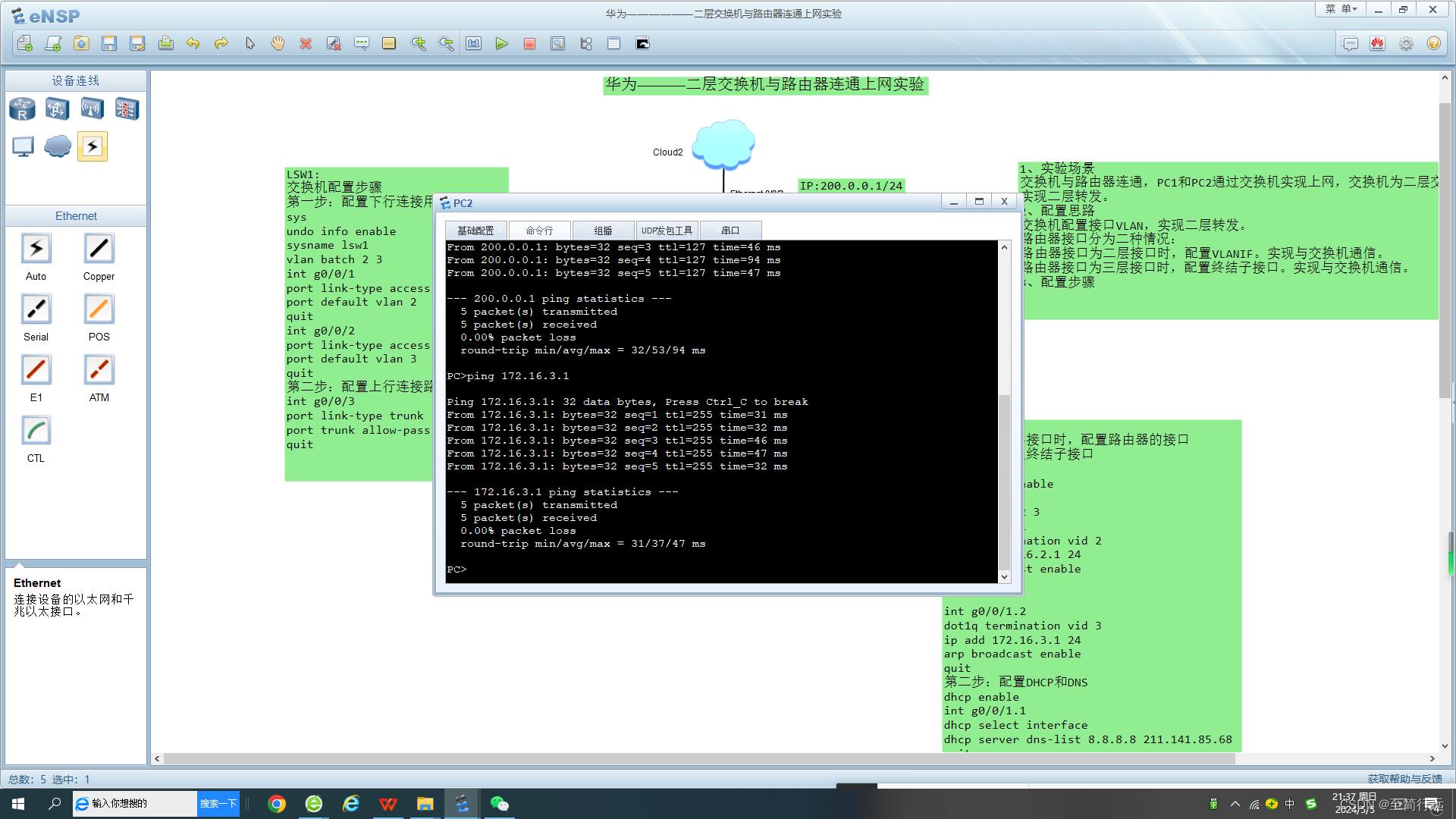
二层交换机与路由器连通上网实验
华为二层交换机与路由器连通上网实验 二层交换机是一种网络设备,用于在局域网(LAN)中转发数据帧。它工作在OSI模型的第二层,即数据链路层。二层交换机通过学习和维护MAC地址表,实现了数据的快速转发和广播域的隔离。 实…...

AJAX知识点(前后端交互技术)
原生AJAX AJAX全称为Asynchronous JavaScript And XML,就是异步的JS和XML,通过AJAX可以在浏览器中向服务器发送异步请求,最大的优势:无需刷新就可获取数据。 AJAX不是新的编程语言,而是一种将现有的标准组合在一起使用的新方式 …...

用wordpress为外贸进出口公司搭建多语言国际站
使用WordPress为外贸进出口公司搭建多语言国际站是一个很好的选择,因为WordPress不仅易于使用,而且具有丰富的插件和主题,可以支持多语言内容。以下是搭建多语言国际站的步骤和建议: 安装WordPress:首先,您…...

雷军-2022.8小米创业思考-6-互联网七字诀之口碑:口碑即定位,超预期才有口碑,品牌建设
第六章 互联网七字诀 专注、极致、口碑、快,这就是我总结的互联网七字诀,也是我对互联网思维的高度概括。 口碑 用户口碑是所有产品成功的关键因素,这是不言而喻的公理。 资源永远有限,对于创业公司尤其如此。只有专注…...

欧盟MDR法规对医疗器械网络安全都有哪些要求?
MDR,欧盟医疗器械法规(Medical Device REGULATION (EU) 2017/745,简称“MDR”),当医疗器械办理欧盟CE认证时,需满足新法规 MDR (EU) 2017/745要求。 M DR符合性评估 医械网络安全咨询与相关文件出具&#x…...
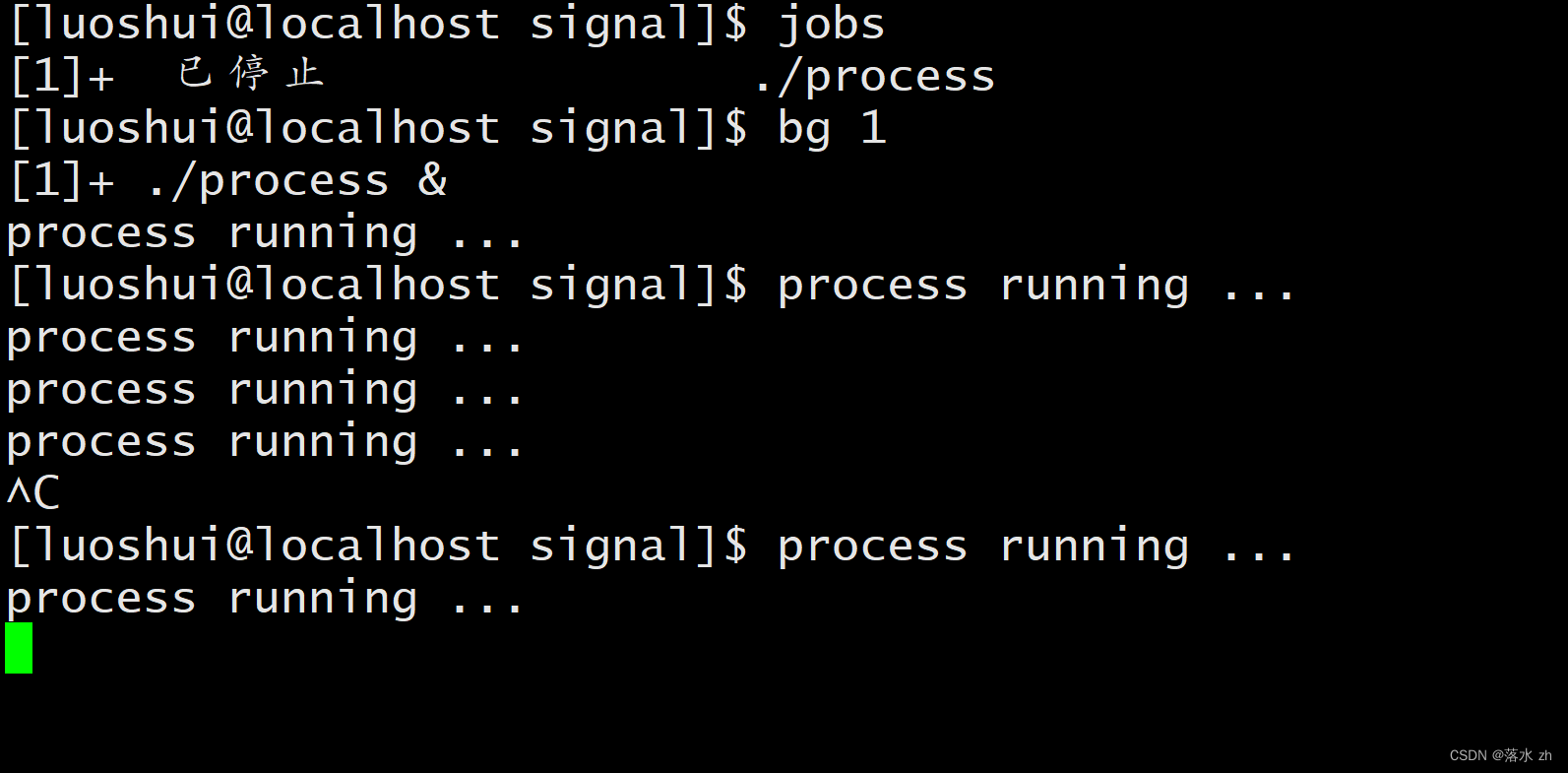
Linux —— 信号初识
Linux —— 信号初识 什么是信号测试几个信号signal函数函数原型参数说明返回值注意事项示例 后台程序前台转后台检测输入中断向量表 我们今天来继续学习Linux的内容,今天我们要了解的是Linux操作系统中的信号: 什么是信号 信号是操作系统内核与进程之…...

webpack进阶 -- 自定义Plugin,Loader封装打包优化
介绍 Webpack 是一个现代 JavaScript 应用程序的静态模块打包器(module bundler)。在 Webpack 处理应用程序时,它会在内部构建一个依赖图(dependency graph),这个依赖图对应映射到项目所需的每个模块,并生成一个或多个 bundle。在这个过程中…...

《Decoupled Optimisation for Long-Tailed Visual Recognition》阅读笔记
论文标题 《Decoupled Optimisation for Long-Tailed Visual Recognition》 长尾视觉识别的解耦优化 作者 Cong Cong、Shiyu Xuan、Sidong Liu、Shiliang Zhang、Maurice Pagnucco 和 Yang Song、 来自新南威尔士大学计算机科学与工程学院、北京大学计算机学院多媒体信息处…...
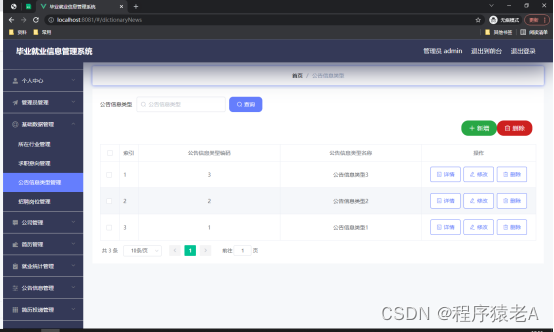
Springboot+Vue项目-基于Java+MySQL的毕业就业信息管理系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...

条件平差——以水准网平差为例 (python详细过程版)
目录 一、原理概述二、案例分析三、代码实现四、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、原理概述 条件平差的函数模型和随机模型为: A V + W = 0...

mysql -- WITH RECURSIVE 语法
引言 在 SQL 中,WITH RECURSIVE 是一个用于创建递归查询的语句。它允许你定义一个 Common Table Expression (CTE),该 CTE 可以引用自身的输出。递归 CTE 非常适合于查询具有层次结构或树状结构的数据,例如组织结构、文件系统或任何其他具有…...

洗地机什么品牌好?洗地机怎么选?618洗地机选购指南
随着科技的飞速发展,洗地机以其高效的清洁能力、稳定的性能和用户友好的设计而闻名,不仅可以高效吸尘、拖地,还不用手动洗滚布,已经逐渐成为现代家庭不可或缺的清洁助手。然而,在众多品牌和型号中,如何选择…...

nginx负载均衡配置
1.nginx负载均衡配置 upstream lbs {server 192.168.1.12:8080;server 192.168.1.12:8081; }server {listen 80;server_name localhost a.com;#charset koi8-r;#access_log logs/host.access.log main;location / {root html;index index.html index.htm;}locatio…...
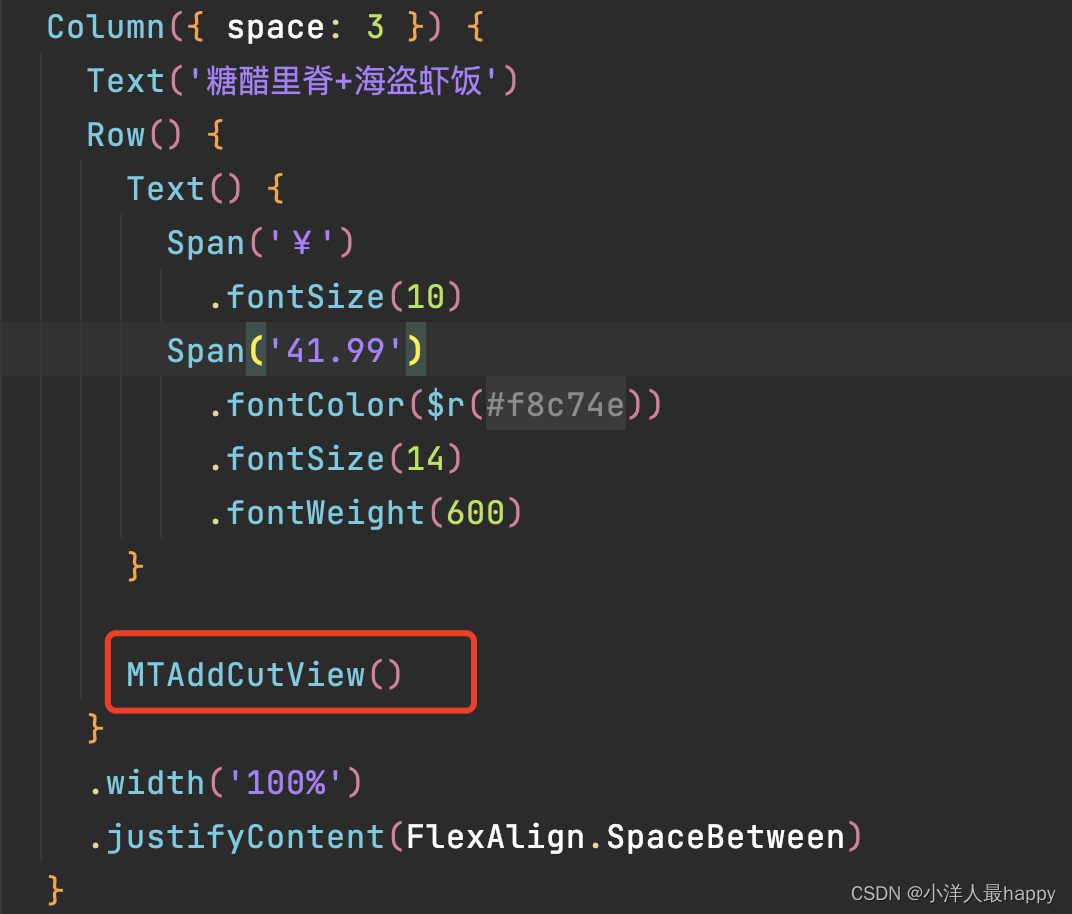
HarmonyOS NEXT星河版之美团外卖点餐功能实战(中)
接上 一、UI布局 1.1 购物车Item Preview Component export struct MTCartItemView {build() {Row({ space: 6 }) {Image(https://bkimg.cdn.bcebos.com/pic/4d086e061d950a7bc94a331704d162d9f3d3c9e2).width(42).aspectRatio(1).borderRadius(5)Column({ space: 3 }) {Text…...

CTF-Web Exploitation(持续更新)
CTF-Web Exploitation 1. GET aHEAD Find the flag being held on this server to get ahead of the competition Hints Check out tools like Burpsuite to modify your requests and look at the responses 根据提示使用不同的请求方式得到response可能会得到结果 使用…...

图书管理系统c语言
创建一个图书管理系统是一个涉及数据结构和文件操作的项目。在C语言中,你可以使用结构体来表示图书信息,使用函数来实现系统的各项功能。以下是一个简单的图书管理系统的示例,包括基本的添加、显示、查找和删除图书的功能。 1. 定义图书结构…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...
