概率论 科普
符号优先级
概率公式中一共有三种符号:分号 ; 、逗号 , 、竖线 | 。
; 分号代表前后是两类东西,以概率P(x;θ)为例,分号前面是x样本,分号后边是模型参数。分号前的 表示的是这个式子用来预测分布的随机变量x,分号后的 表示所需的相关参数θ。
, 逗号代表两个事件同时发生的概率,逗号连接两个事件,有时可以省略,如联合概率P(AB),等价于P(A,B)
| 竖线代表 if,以条件概率P(A|B)为例,A,B是随机试验E的两个随机试验,P(A|B)就是如果B事件发生的条件下,发生A事件的概率,结合图进行理解:
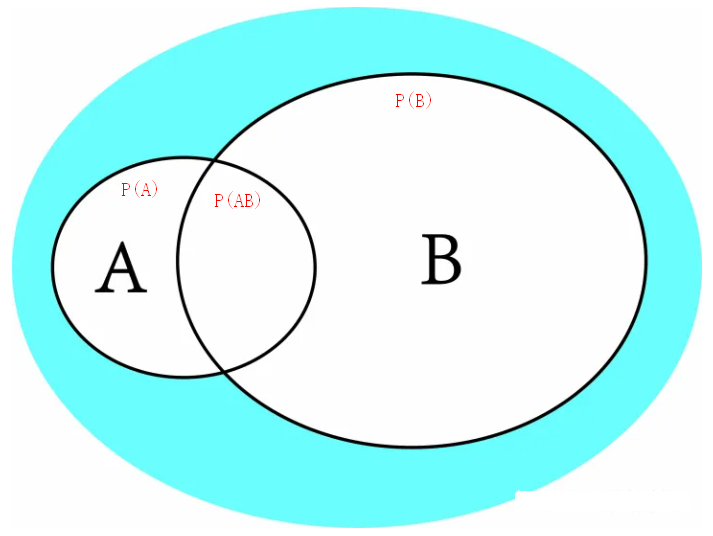
优先级: , > | > ;
例子1: P(A|B,C)表示在B,C的条件下,发生A的概率。
例子2:P(y∣x ; α,ω)表示:x发生条件下y的条件概率,该条件概率模型用参数α,ω建模(或者说用参数a,ω表示)。
注意:
p ( x ∣ θ ) p(x | \theta) p(x∣θ)不总是代表条件概率,也就是说 p ( x ∣ θ ) p(x | \theta) p(x∣θ) 不代表条件概率时与 p ( x ; θ ) p(x ; \theta) p(x;θ) 等价。而一般地,写竖杠表示条件概率,是随机变量。
p ( x ; θ ) p(x ; \theta) p(x;θ) 中,分号后的 表示待估参数(是固定的,只是当前未知),应该可以直接认为是 p ( x ) p(x) p(x),加了,是为了强调说明这里有个 θ \theta θ 的参数, p ( x ; θ ) p(x ; \theta) p(x;θ) 意思是随机变量 X = x X=x X=x 的概率。在 贝叶斯理论下又叫 X = x X=x X=x 的先验概率。
和 扩散模型推导公式的联系
根据以上讨论的这些,现在讨论一个比较复杂的情况。比如, N ( x ; 0 , I ) \mathcal{N}(x;0,I) N(x;0,I)的意思是什么?
我们知道, N ( 0 , I ) \mathcal{N}(0,I) N(0,I)表示标准高斯分布,均值为0,方差为1,其本质上也是一个概率密度函数 f ( x ) = 1 σ 2 π e − 1 2 ( x − μ σ ) 2 f(x) = \frac{1}{{\sigma \sqrt{2\pi}}} e^{ -\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} f(x)=σ2π1e−21(σx−μ)2(标准高斯分布情况下为 f ( x ) = 1 2 π e − x 2 2 f(x) = \frac{1}{{\sqrt{2\pi}}} e^{ -\frac{x^2}{2}} f(x)=2π1e−2x2 )。从这里可以发现,一般的函数我们都是强调自变量本身(比如 x x x),而在概率论里面有时候强调的是函数参数本身(比如高斯分布的均值和方差),而淡化了输入变量 x x x。因此 N ( x ; 0 , I ) \mathcal{N}(x;0,I) N(x;0,I)相比与 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)的区别就在于显式强调了函数的输入为 x x x。
这下,就好理解扩散模型中的噪声公式了:

那么, q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t | x_{t-1})=\mathcal{N}(x_t; \sqrt{1-\beta_t }x_{t-1}, \beta_t I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI),这个公式何意义?
这个东西分多步看。首先,函数本身是个条件概率分布, q ( x t ∣ x t − 1 ) q(x_t | x_{t-1}) q(xt∣xt−1) 表示 x t − 1 x_{t-1} xt−1 已知的情况下, x t x_t xt 的分布 ( x t x_t xt取各种值的概率)。而后面的这个高斯分布则强调了其输入自变量为 x t x_t xt(因为是 x t x_t xt的概率密度函数,所以自变量当然是 x t x_t xt),而高斯分布的均值和方差则分别为
1 − β t x t − 1 和 β t I \sqrt{1-\beta_t }x_{t-1} 和 \beta_t I 1−βtxt−1和βtI,与条件分布的条件 x t − 1 x_{t-1} xt−1 有关。
全概率(概率函数连乘)

图示可表示为:
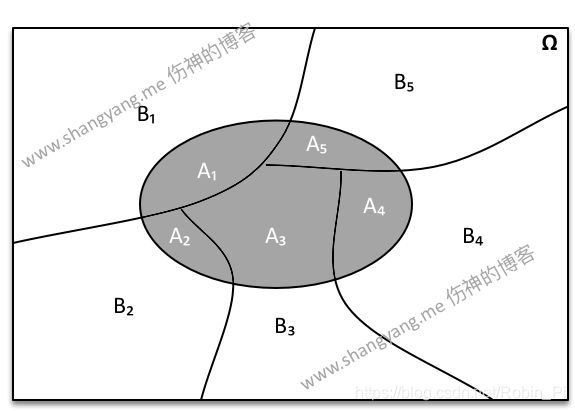
参考:
https://blog.csdn.net/shyjhyp11/article/details/133969095
相关文章:

概率论 科普
符号优先级 概率公式中一共有三种符号:分号 ; 、逗号 , 、竖线 | 。 ; 分号代表前后是两类东西,以概率P(x;θ)为例,分号前面是x样本,分号后边是模型参数。分号前的 表示的是这个式子用来预测分布的随机变量x,分号后的…...
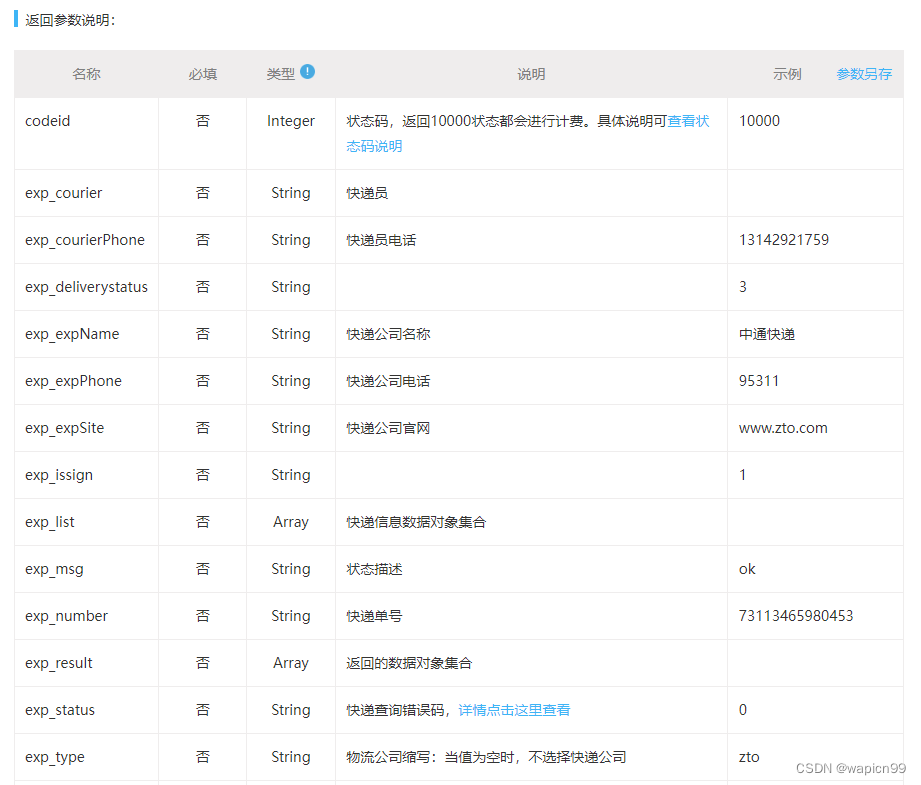
全面解读快递查询API接口,帮你轻松查询快递物流信息
随着电子商务的快速发展,快递业务正变得越来越重要。无论是买家还是卖家,都希望能够及时了解自己的快递物流信息,以便更好地掌控商品的运输过程。而现在,通过快递查询API接口,我们可以实现快速、准确地查询几百家国内快…...

【图书推荐】《JSP+Servlet+Tomcat应用开发从零开始学(第3版)》
本书目的 系统讲解JSPServletTomcat开发技术,帮助读者用最短的时间掌握Java Web应用开发技能。 内容简介 本书全面系统地介绍JSPServletTomcat开发中涉及的相关技术要点和实战技巧。本书内容讲解循序渐进,结合丰富的示例使零基础的读者能够熟练掌握JSP…...

C++容器——set
set容器 是一个关联容器,按一定的顺序存储一组唯一的元素。 set容器中的元素会根据元素的值自动进行排序,并且不允许包含重复的元素,基于二叉树实现的。 特点: 唯一性: set容器中的元素是唯一的,即容器中…...

.NET WebService \ WCF \ WebAPI 部署总结 以及 window 服务 调试
一、webservice 部署只能部署IIS上, 比较简单,就不做说明了 二、 WCF 部署 1 部署到IIS 跟部署 webservice 部署方法一样的 wcf 部署2 部署到控制台 要以管理员运行vs,或者 管理员运行 控制台的exe 在控制器项目中 创建IUserInfoService 接口…...
)
Centos系统实用运维命令记录(持续更新)
本文记录Centos服务器常用的运维命令,备忘 查询当前内存占用最高(前10)的进程列表和占用比例,进程ID ps -eo pid,comm,%mem,cmd --sort-%mem | head -n 11注: 内存警报时定位问题时非常有用 查询占用某个端口号的进程id lsof -i :9000注: 后面的9000…...

大势模方在修模过程中,如何导入su单体模型?
答:在单体化界面右键即可显示导入入口,若仍不可行,需要换最新版dv 模方是一款针对实景三维模型的冗余碎片、水面残缺、道路不平、标牌破损、纹理拉伸模糊等共性问题研发的实景三维模型修复编辑软件。模方4.1新增自动单体化建模功能ÿ…...

uniapp百度地图聚合
// loadBMap.js ak 百度key export default function loadBMap(ak) {return new Promise((resolve, reject) > {//聚合API依赖基础库,因此先加载基础库再加载聚合APIasyncLoadBaiduJs(ak).then(() > {// 调用加载第三方组件js公共方法加载其他资源库// 加载聚合API// Ma…...
nginx的应用部署nginx
这里写目录标题 nginxnginx的优点什么是集群常见的集群什么是正向代理、反向代理、透明代理常见的代理技术正向代理反向代理透明代理 nginx部署 nginx nginx(发音同enginex)是一款轻量级的Web服务器/反向代理服务器及电子邮件(IMAP/POP3&…...
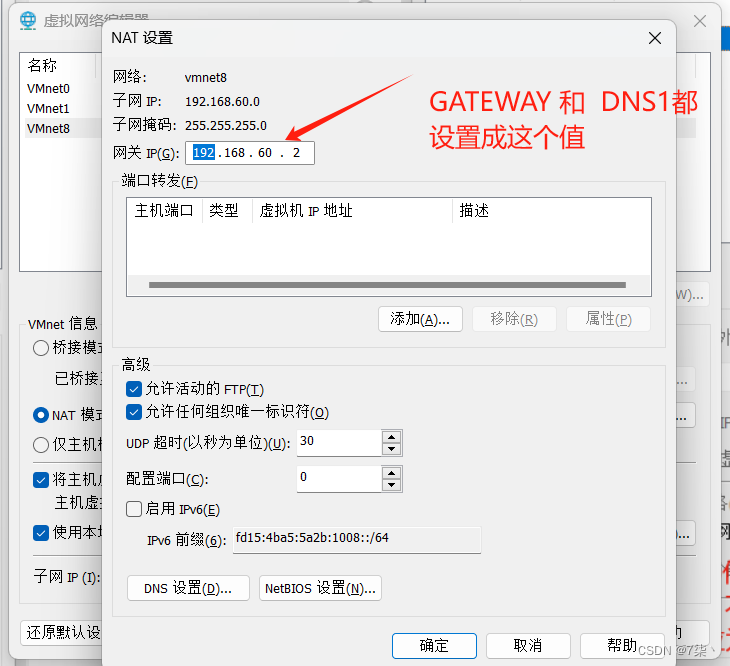
Centos固定静态ip地址
这里我用的是Vmware虚拟机搭建的三台机器 进入 cd /etc/sysconfig/network-scripts然后使用 ip addr命令,查看自己虚拟机的以太网地址。 我这里是ens33 上面的第一个选项是本地环回地址,不用管它 然后查看刚刚进入的network-scripts目录下的文件 找到…...

豆芽机置入语音芯片WTN6040-8S:开启智能生活新篇章,让豆芽制作更便捷有趣
豆芽机的开发背景: 豆芽作为一种营养丰富、味道鲜美的食品,深受广大消费者的喜爱。然而,传统的豆芽生产过程繁琐,需要耗费大量的时间和人力,且存在生产效率低、质量不稳定等问题。随着人们生活节奏的加快和对健康饮食的…...
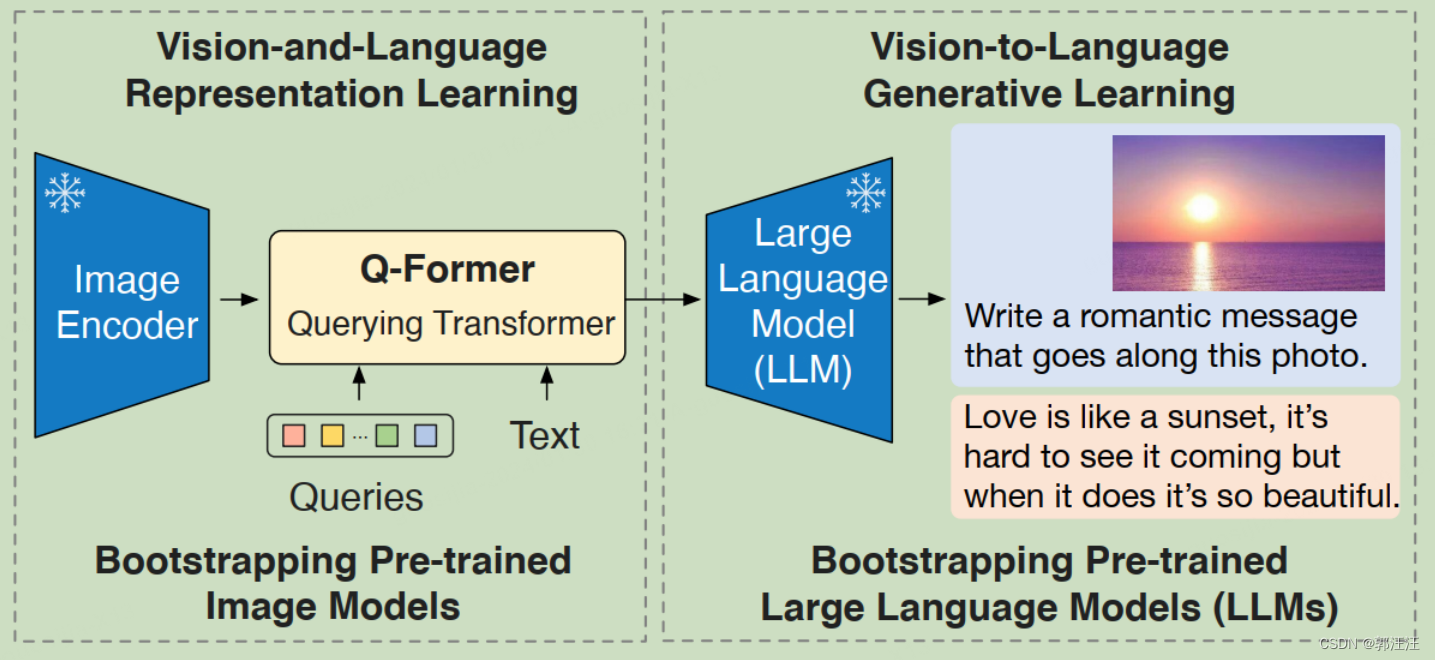
BLIP2预研笔记
0. 前言 文章是公司内部分享学习写的预研报告,里面有小部分文段是直接从网上借鉴的,侵删 1. 任务和方法历史进化: 在大模型等类似的预训练模型的方式(以包含“预训练阶段”等n阶段训练方式为特色)为主流之前…...

安卓开发问题:安卓Ble出现动态鉴权失败以及扫描设备一直进入不了的问题
问题1描述 1、安卓12需要动态鉴权 // 鉴权函数 requestPermissions(permissionsList.toArray(strings), MyConstants.REQUEST_CODE_PERMISSIONS);但是在鉴权回调函数中如Manifest.permission.BLUETOOTH_SCAN、Manifest.permission.BLUETOOTH_CONNECT一直显示失败&…...
DSP ARM FPGA 实验箱_音频处理_滤波操作教程:3-9 音频信号的滤波实验
一、实验目的 掌握Matlab辅助设计滤波器系数的方法,并实现音频混噪及IIR滤波器滤除,并在LCD上显示音频信号的FFT计算结果。 二、实验原理 音频接口采用的是24.576MHz(读兆赫兹)晶振,实验板上共有3个音频端口&#x…...

Rust多线程交叉打印+Send Sync特征讲解
导航 Rust多线程交叉打印Send Sync特征讲解 一、Rust多线程交叉打印二、Send Sync 特征讲解 Rust多线程交叉打印Send Sync特征讲解 一、Rust多线程交叉打印 先说背景有两个线程,分别为0号线程和1号线线程两个线程交叉打印共享值,并将共享值1当标志为fa…...

C#爬虫爬取某东商品信息
🏆作者:科技、互联网行业优质创作者 🏆专注领域:.Net技术、软件架构、人工智能、数字化转型、DeveloperSharp、微服务、工业互联网、智能制造 🏆欢迎关注我(Net数字智慧化基地),里面…...
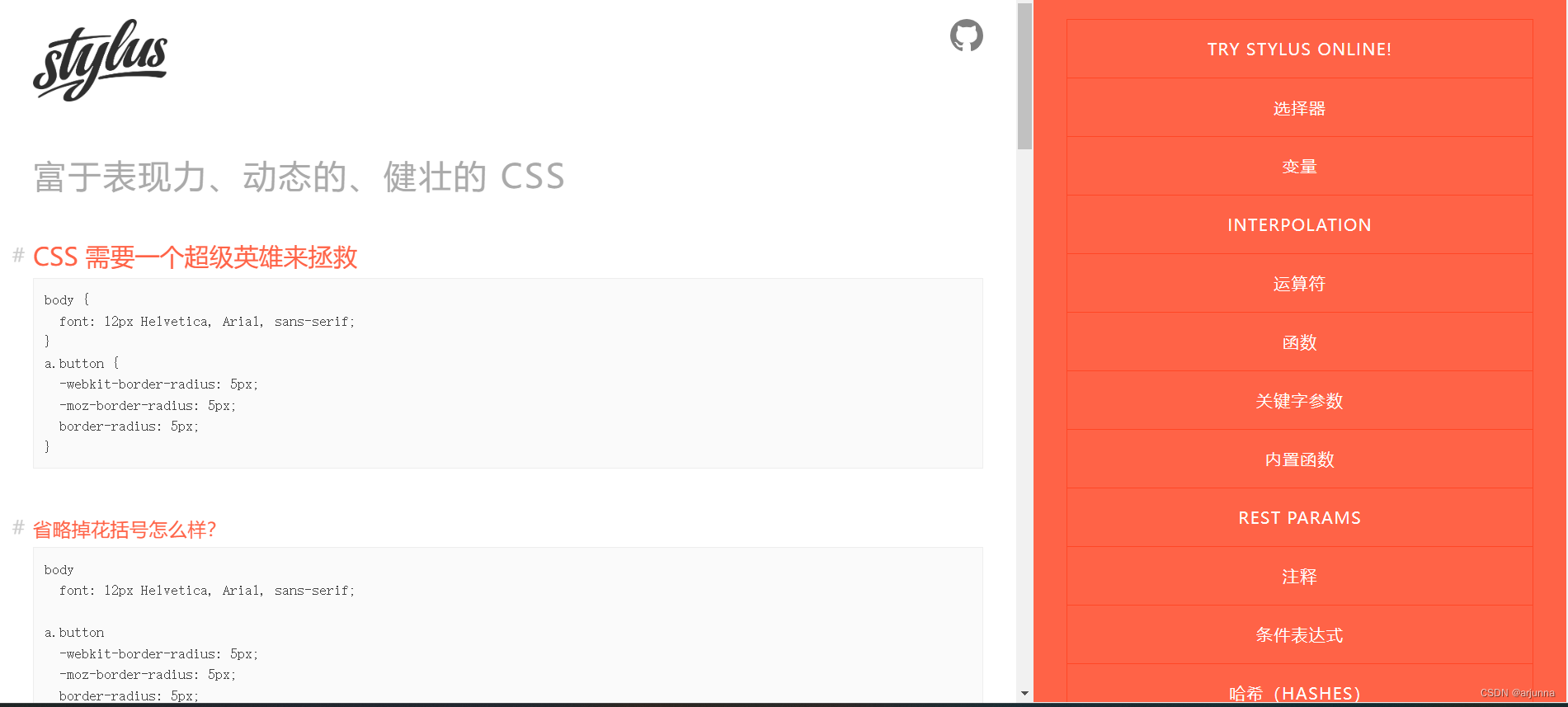
【Stylus详解与引入】
文章目录 Stylus详解与引入一、Stylus简介二、Stylus的特性1. 变量2. 嵌套规则3. 混合(Mixins)4. 函数5. 条件语句和循环 三、Stylus的引入与配置1. 安装Stylus和stylus-loader2. 配置Webpack3. 在Vue项目中使用Stylus4. 编译Stylus代码四、Stylus的性能…...
)
001 登录(md5加密)
文章目录 pom.xmlLoginController.javaUserMapper.javaUser.javaUserServiceImpl.javaUserService.javaMD5Util.javaMD5UtilTest.javaValidatorUtil.javaLoginVo.javaRespBean.javaRespBeanEnum.javaSeckillApplication.javaUserMapper.xmllogin.htmlapplication.yamlsql 传统方…...
Linux学习笔记5---WSL2编译裸机程序并烧录至SD卡
在用WLS进行开发的时候发现在mnt/底下竟然识别不了U盘!!也识别不了SD卡!!那程序不就不能烧录到SD卡上了???那还开发个锤子。 在网上查找了一些相关资料,发现可以通过Win32DiskImager…...
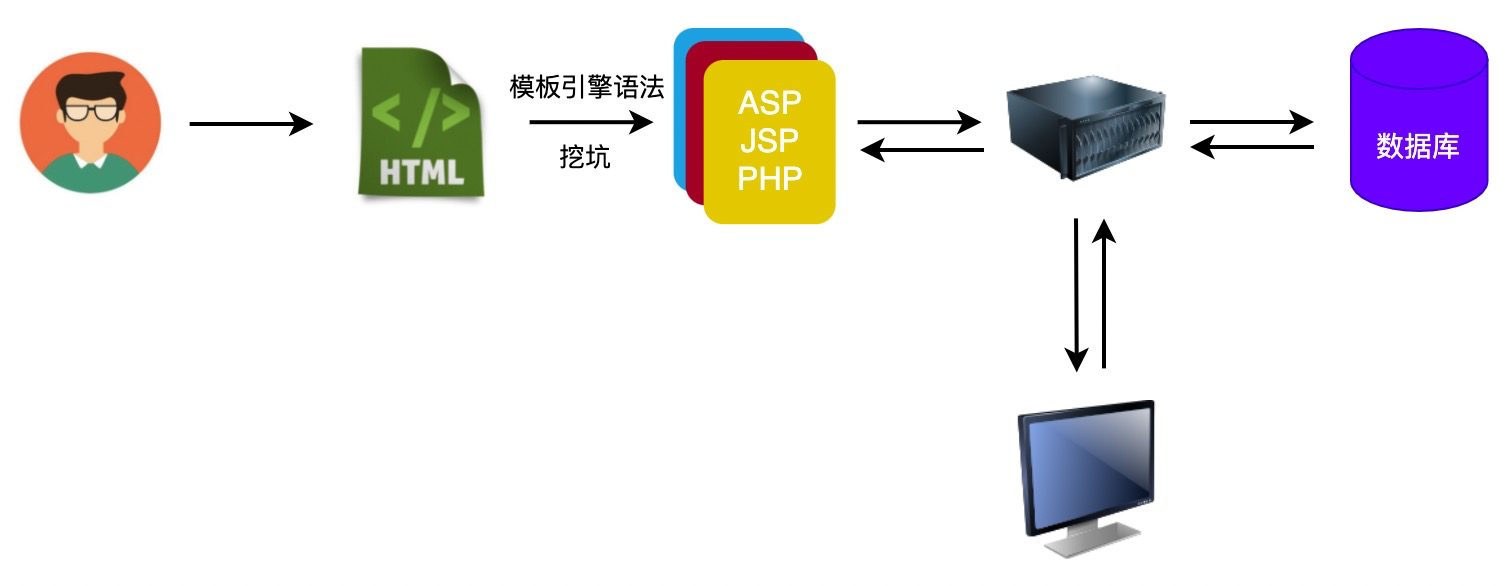
React 第二十九章 React 和 Vue 描述页面的区别
面试题:React 和 Vue 是如何描述 UI 界面的?有一些什么样的区别? 标准且浅显的回答: React 中使用的是 JSX,Vue 中使用的是模板来描述界面 前端领域经过长期的发展,目前有两种主流的描述 UI 的方案…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
