a-auto-complete 请求后端数据做模糊查询,解决下拉框选择选不上,不回显的问题
a-auto-complete 请求后端数据做模糊查询,解决下拉框选择选不上,不回显的问题
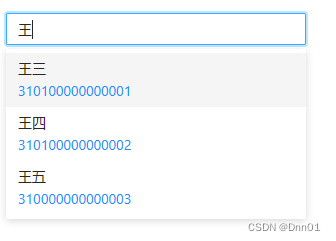
记录一个a-auto-complete卡bug卡了两天,找不到哪里的问题下拉框选择选不上,不回显,最后终于解决了。
我还对下拉框显示的内容做了小调整。
直接看代码吧。
<a-auto-complete v-model:value="inputValue" :options="personOptions" style="width: 300px" placeholder="请输入姓名"@select="onSelect" @search="onSearch"><template #option="item"><span>{{ item.name }}</span><br /><span style="color:#1890ff">{{ item.licenseNumber }}</span></template></a-auto-complete>..................
//input值
const inputValue = ref('');
//下拉框option
const personOptions = ref([]);
//输入的事件
const onSearch = searchText => {
//发送请求获取option数组const param = {name: searchText}relationApi.getPerson(param).then((res) => {///卡bug的地方就在这,请求接口返回的数据了没有value这个字段,所以要给option数组里的对象添加value属性///option数组里需要name和value属性!const a = res.map(item => {return {...item,value: item.name}})personOptions.value = !searchText? []: a;}).finally(() => {})
};
//选择下拉框的事件
const onSelect = (value, option) => {
/value是下拉框选中的值,option是选中的所有属性,可以取你自己想要的值,我这里取的是option.licenseNumbe,然后自己进行后续操作。relationApi.getPersonDetial({ licenseNumber: option.licenseNumber }).then((res) => {if (res.body) {treeData.value = res.body} else {message.warning('暂无数据!')treeData.value = []}initTree();}).finally(() => {})
};
相关文章:

a-auto-complete 请求后端数据做模糊查询,解决下拉框选择选不上,不回显的问题
a-auto-complete 请求后端数据做模糊查询,解决下拉框选择选不上,不回显的问题 记录一个a-auto-complete卡bug卡了两天,找不到哪里的问题下拉框选择选不上,不回显,最后终于解决了。 我还对下拉框显示的内容做了小调整。…...

Leetcode—724. 寻找数组的中心下标【简单】
2024每日刷题(129) Leetcode—724. 寻找数组的中心下标 实现代码 class Solution { public:int pivotIndex(vector<int>& nums) {int sum accumulate(nums.begin(), nums.end(), 0);int prefix 0;for(int i 0; i < nums.size(); i) {i…...

C语言 | Leetcode C语言题解之第72题编辑距离
题目: 题解: static inline int Min(const int a, const int b, const int c) {int min (a < b) ? a : b;return (min < c) ? min : c; }int minDistance(char * word1, char * word2){int m strlen(word1), n strlen(word2);int dp[m 1][n…...

AI视频教程下载:零代码创建AI智能体、AI Agents和ChatGPT的Gpts
这门课程专注于提示工程的掌握,教你以精确的方式引导GPT,利用它们的生成能力产生卓越的AI驱动结果。一步一步地,你将学会创建多样化的GPT军团——每个都设计来满足特定的专业需求。 从提供个性化职业变更指导的职业教练AI,到以惊…...

汽车之家,如何在“以旧换新”浪潮中大展拳脚?
北京车展刚刚落幕,两重利好正主导汽车市场持续升温:新能源渗透率首破50%,以及以旧换新详细政策进入落地期。 图源:中国政府网 在政策的有力指引下,汽车产业链的各个环节正经历着一场深刻的“连锁反应”。在以旧换新的…...
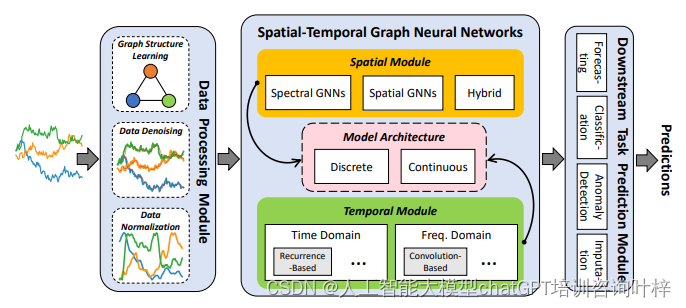
图神经网络(GNNs)在时间序列分析中的应用
时间序列数据是记录动态系统测量的主要数据类型,由物理传感器和在线过程(虚拟传感器)大量生成。时间序列分析对于解锁可用数据中隐含的丰富信息至关重要。随着图神经网络(GNNs)的最近进展,基于GNN的方法在时…...

Qt QShortcut快捷键类详解
1.简介 QShortcut是一个方便的工具类,用于在应用程序中创建快捷键。通过设置快捷键和关联的处理函数,可以实现快速执行某个操作的功能。 // 创建一个快捷键,关联到MyWidget类的keyPressEvent()函数 QShortcut *shortcut new QShortcut(QKe…...

003 redis分布式锁 jedis分布式锁 Redisson分布式锁 分段锁
文章目录 Redis分布式锁原理1.使用set的命令时,同时设置过期时间2.使用lua脚本,将加锁的命令放在lua脚本中原子性的执行 Jedis分布式锁实现pom.xmlRedisCommandLock.javaRedisCommandLockTest.java 锁过期问题1乐观锁方式,增加版本号(增加版本…...

Jackson工具,java对象和json字符串之间的互相转换
一、maven依赖引入jackson <dependency><groupId>com.fasterxml.jackson.core</groupId><artifactId>jackson-databind</artifactId><version>2.12.5</version></dependency>jackson-databind依赖见下: <depend…...

【设计模式】之装饰器模式
系列文章目录 【设计模式】之模板方法模式 【设计模式】之责任链模式 【设计模式】之策略模式 【设计模式】之工厂模式(三种) 前言 今天给大家介绍23种设计模式中的装饰器模式。🌈 一、什么是装饰器模式 装饰器模式(Decora…...

leetcode_46.全排列
46. 全排列 题目描述:给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2&#…...
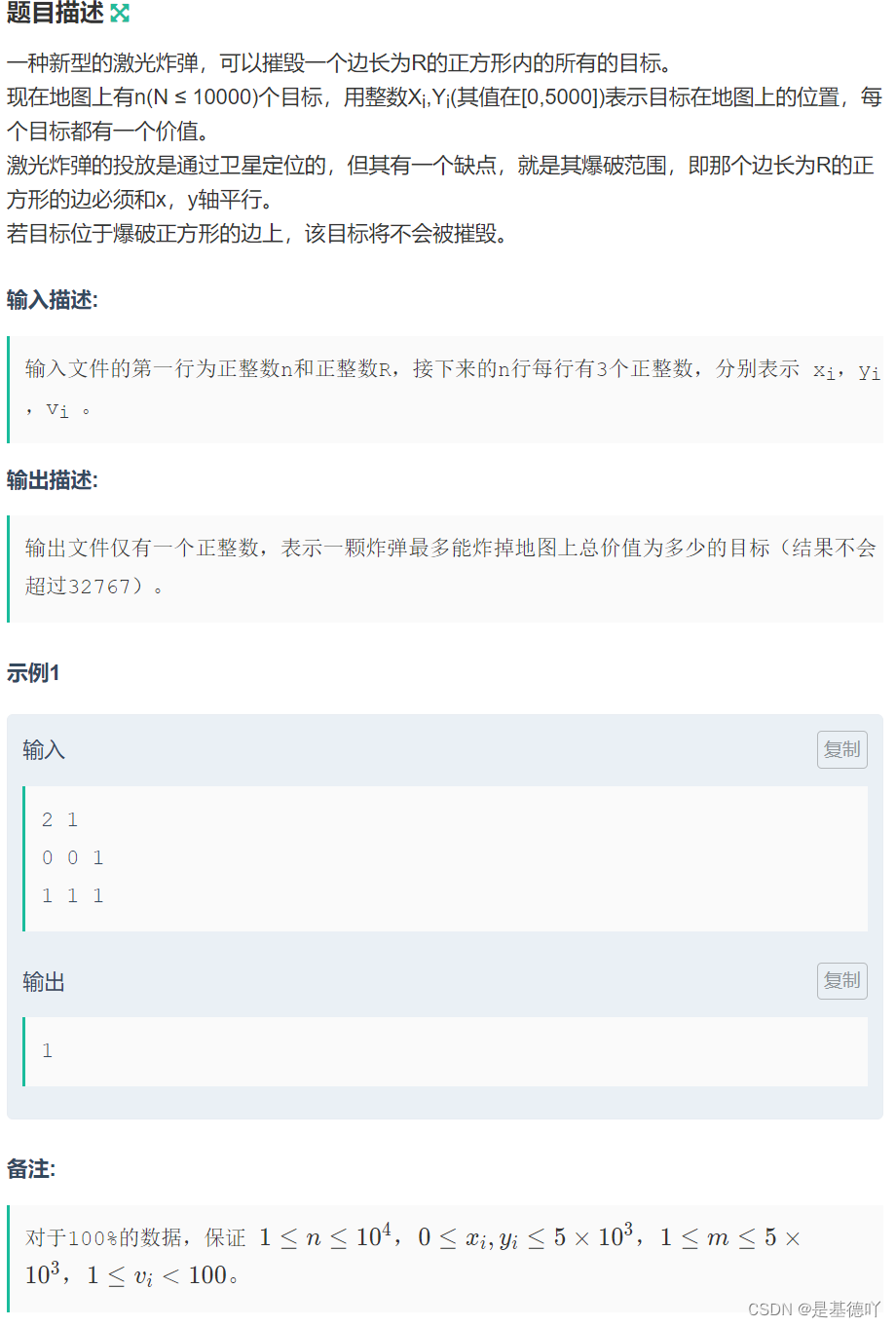
【牛客】[HNOI2003]激光炸弹
原题链接:登录—专业IT笔试面试备考平台_牛客网 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 二维前缀和板题。 注意从(1,1)开始存即可,所以每次输入x,y之后,要x,y。 因为m的范围最大为…...

Docker与Harbor:构建企业级私有Docker镜像仓库
目录 引言 一、本地私有仓库 (一)基本概述 (二)搭建本地私有仓库 1.下载registry镜像 2.启动容器 3.上传本地镜像 4.客户端下载镜像 二、Harbor简介 (一)什么是 Harbor (二ÿ…...

推荐几个傻瓜式短视频去水印在线网站
在数字化时代,短视频已成为信息传播的重要方式之一。随着TikTok、Instagram Reels、抖音等平台的流行,短视频的制作和分享成为了日常生活的一部分。然而,在分享或编辑这些短视频时,去除水印成为了一项不可或缺的需求。水印是视频原…...
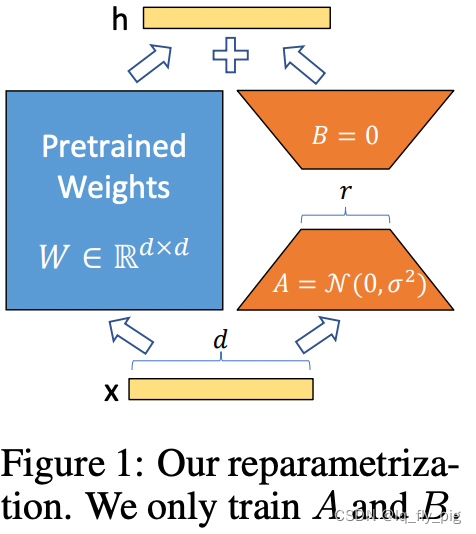
大模型LLM之SFT微调总结
一. SFT微调是什么 在大模型的加持下现有的语义理解系统的效果有一个质的飞跃;相对于之前的有监督的Pre-Train模型;大模型在某些特定的任务中碾压式的超过传统nlp效果;由于常见的大模型参数量巨大;在实际工作中很难直接对大模型训…...
【RocketMQ问题总结-2】
RocketMQ 消息持久化 Broker通过底层的Netty服务器获取到一条消息后,会把这条消息的内容写入到一个CommitLog文件里去(一个Broker进程就只有一个CommitLog文件,也就是说这个Broker上所有Topic的消息都会写入这个文件)。 同时&…...

掌握Android Fragment开发之魂:Fragment的深度解析(上)
Fragment是Android开发中用于构建动态和灵活界面的基石。它不仅提升了应用的模块化程度,还增强了用户界面的动态性和交互性,允许开发者将应用界面划分为多个独立、可重用的部分,每个部分都可以独立于其他部分进行操作。本文将从以下几个方面深…...

深度解读DreamFusion:一站式AI解决方案
DreamFusion是一款备受瞩目的人工智能解决方案,它整合了多种AI技术,为用户提供了一站式的解决方案。本文将全面解读DreamFusion,探讨其特点、功能和应用场景,助您深入了解这一创新工具。 1. 特点概述 DreamFusion具备以下显著特…...

JVM-02
字节码文件是一种特殊的文件格式,它包含了将源代码转换为机器可执行代码所需的指令集。字节码文件通常是由编译器将源代码编译为字节码的中间表示形式。 在Java中,字节码文件的扩展名为.class,它存储了编译后的Java代码。这些字节码文件可以在…...

【一起深度学习——NIN】
NIN神经网络 原理图:代码实现:输出结果: 原理图: 代码实现: import torch from torch import nn from d2l import torch as d2ldef nin_block(in_channels, out_channels, kernel_size, strides, padding):return nn.…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
