数据结构(八)排序
一、排序的概念以及引用
概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
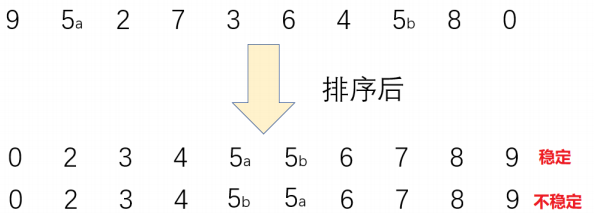
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
常见的排序算法
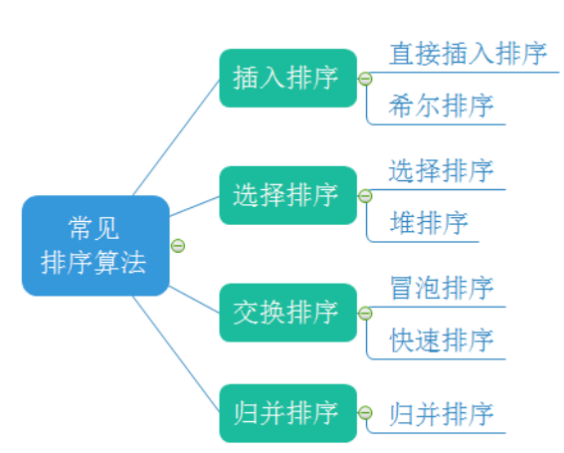
二、常见排序算法的实现
插入排序
基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。实际中我们玩扑克牌时,就用了插入排序的思想。
直接插入排序
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移
直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
public static void insertSort(int[] array){for (int i = 0; i < array.length; i++) {int tmp=0;for (int j = i-1; j >=0 ; j--) {if (array[i]>=array[j]){break;}else {tmp = array[i];array[i] = array[j];array[j] = tmp;i--;}}}}希尔排序( 缩小增量排序 )
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
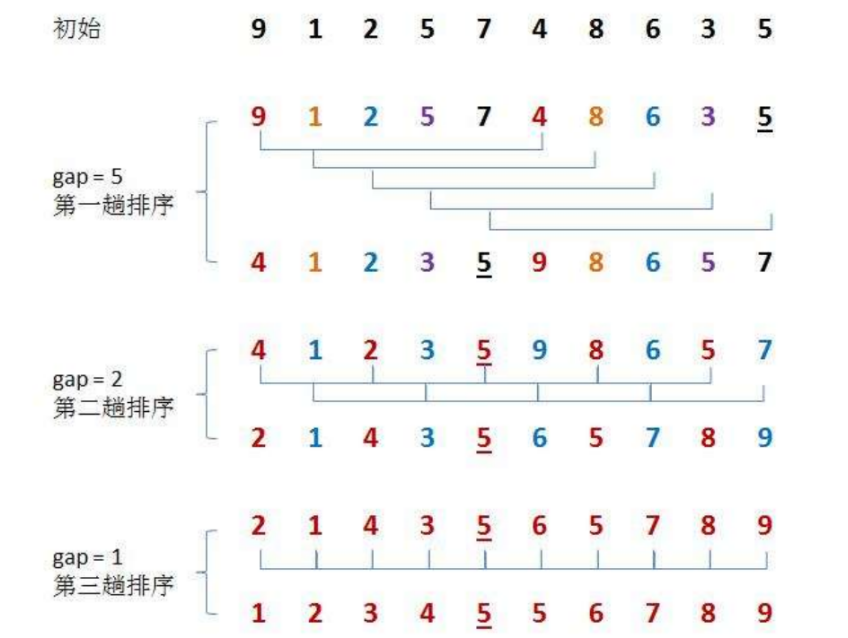
希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定
4. 稳定性:不稳定
public static void shell(int[] array,int gap){for (int i = gap; i < array.length; i++) {int tmp=array[i];int j=i-gap;for (; j >=0 ; j=j-gap) {if (tmp>=array[j]){break;}else {array[j+gap]=array[j];}}array[j+gap]=tmp;}}public static void shellSort(int[] array){int gap=array.length;while (gap>1){gap/=2;shell(array,gap);}shell(array,1);}选择排序
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
直接选择排序:
1、在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素
2、若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
3、在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
【直接选择排序的特性总结】
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {for (int j = i+1; j < array.length; j++) {if (array[i]>array[j]){int tmp=array[j];array[j]=array[i];array[i]=tmp;}}}
}堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
【直接选择排序的特性总结】
1. 堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
冒泡排序
【冒泡排序的特性总结】
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:稳定
快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
public static void quickSort(int[] array){quick(array,0,array.length-1);}private static int threeMid(int[] array,int left,int right){int mid=(left+right)>>>2;if (array[left]<array[right]){if (array[mid]<array[left]){return left;}else if (array[mid]>array[right]){return right;}else {return mid;}}else if(array[right]<array[left]){if (array[mid]<array[right]){return right;}else if (array[mid]>array[left]){return left;}else {return mid;}}return -1;}private static void quick(int[] array,int start,int end){if (start>=end){return;}//三数取中法int index=threeMid(array,start,end);int tmp=array[index];array[index]=array[start];array[start]=tmp;int pivot=partition(array,start,end);quick(array, start, pivot-1);quick(array,pivot+1,end);}上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。
归并排序
基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
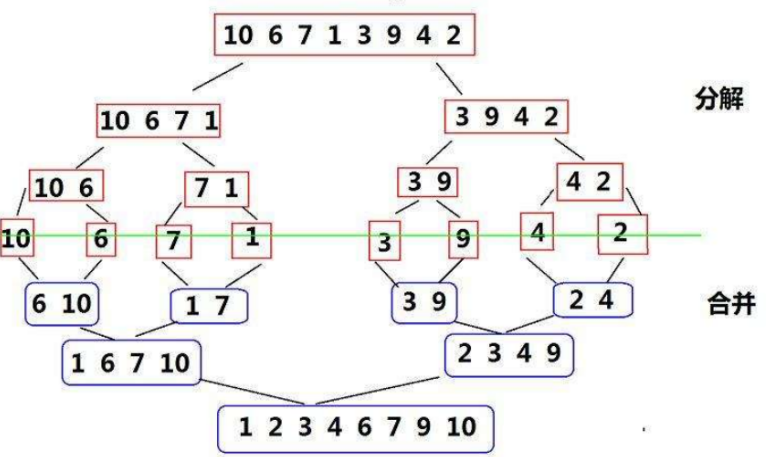
归并排序总结
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
public static void mergeSort(int[] array){mergeSortFunction(array,0,array.length-1);}private static void mergeSortFunction(int[] array,int low,int high){if (low>=high){return;}int mid=(low+high)>>>1;mergeSortFunction(array,low,mid);mergeSortFunction(array,mid+1,high);merge(array,low,high,mid);}private static void merge(int[] array,int low,int high,int mid){int[]tmp=new int[high-low+1];int k=0;int s1=low;int e1=mid;int s2=mid+1;int e2=high;while (s1<=e1&&s2<=e2){if (array[s1]<=array[s2]){tmp[k++]=array[s1++];}else {tmp[k++]=array[s2++];//后置++}}while (s1<=e1){tmp[k++]=array[s1++];}while (s2<=e2){tmp[k++]=array[s2++];}for (int i = 0; i < k; i++) {array[i+low]=tmp[i];}}//非递归public static void mergeSort2(int[] array){int gap=1;while (gap<array.length){for (int i = 0; i < array.length; i+=2*gap) {int low=i;int mid=low+gap-1;if (mid>=array.length){mid=array.length-1;}int high=mid+gap;if (high>=array.length){high=array.length-1;}merge(array,low,high,mid);}gap=gap*2;}}海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
1. 先把文件切分成 200 份,每个 512 M
2. 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
3. 进行 200 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
相关文章:

数据结构(八)排序
一、排序的概念以及引用概念排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,…...

函数习题:用函数实现判断一个整数是否能被n整除
Description 输入一组整数,输入0结束(这组整数不包含0),输出其中能被n整除的所有整数之和(n为整数,不用考虑n为0的情况), n及这组整数均由键盘输入。首先输入n,再输入一…...

SAP 创建会计冲销凭证
“功能描述:根据传输过来数据创建会计冲销凭证,并返回消息和状态 *”---------------------------------------------------------------------- "“本地接口: *” IMPORTING *" VALUE(IW_ZTFKCX0010) TYPE ZTFKCX0010 *" EXP…...
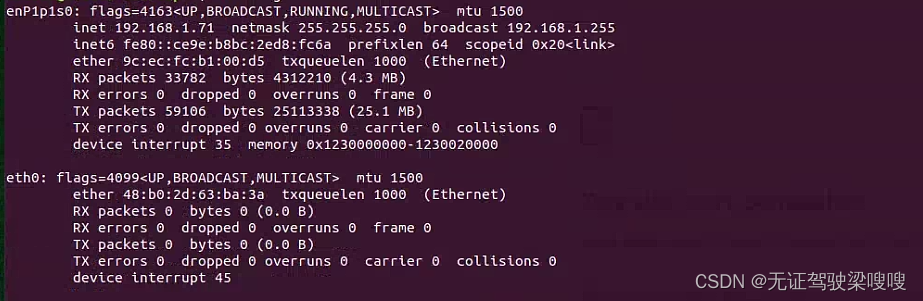
Jetson(Ubuntu18.04)设备无法ping通百度能ping通局域网错误集合,(神奇的是这样的情况下Todesk等远程确没有问题)
一、.打开DNS,意思是取消注释添加114.114.114.114 ,文件如下 vim /etc/systemd/resolved.conf [Resolve] #DNS #FallbackDNS #Domains #LLMNRno #MulticastDNSno #DNSSECno #Cacheyes #DNSStubListeneryes然后重启服务sudo systemctl restart systemd-resolved.se…...

Spring的@Conditional注解
前言Conditional是Spring4新提供的注解,它的作用是按照一定的条件进行判断,满足条件给容器注册bean。Conditional的源码定义://此注解可以标注在类和方法上 Target({ElementType.TYPE, ElementType.METHOD}) Retention(RetentionPolicy.RUNTI…...

剑指 Offer 67 把字符串转换成整数
摘要 面试题67. 把字符串转换成整数 一、字符串解析 根据题意,有以下四种字符需要考虑: 首部空格: 删除之即可;符号位:三种情况,即 , − , 无符号";新建一个变量保存符号位࿰…...

【教学典型案例】18.开门小例子理解面向对象
目录一:背景介绍业务场景:业务分析:二:实现思路1、面向过程:2、面向对象(抽象、封装、继承、多态)3、面向对象(抽象、封装、继承、多态、反射)三:实现过程1、…...

Linux环境ENV的概念
一、基本概念 环境变量的含义:程序(操作系统命令和应用程序)的执行都需要运行环境,这个环境是由多个环境变量组成的。 按变量的周期划为永久变量和临时性变量2种: 永久变量:通过修改配置文件,…...

AcWing数据结构 - 数据结构在算法比赛中的应用(下)
目录 Trie树 Trie字符串统计 最大异或对 并查集 合并集合 连通块中点的数量 食物链 堆 堆排序 模拟堆 哈希表 模拟散列表 字符串哈希 Trie树 Trie字符串统计 思路: 设 idx索引用于构建树, 结点son[节点位置][节点分支指针],cnt[]记录单…...
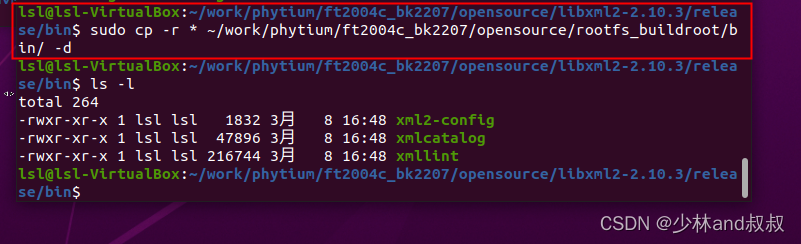
基于嵌入式libxml2的ARM64平台的移植(aarch64)
由于libxml在移植过程中依赖于zlib的库文件,因此本节内容包含zlib(V1.2.13)的移植libxml2(V2.10.3)的移植两部分组成。 (一)zlib的移植(基于arm64) 1、在github上下载zlib的最新源码压缩包&am…...
)
8. 字符串转换整数 (atoi)
题目描述 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 1&#x…...
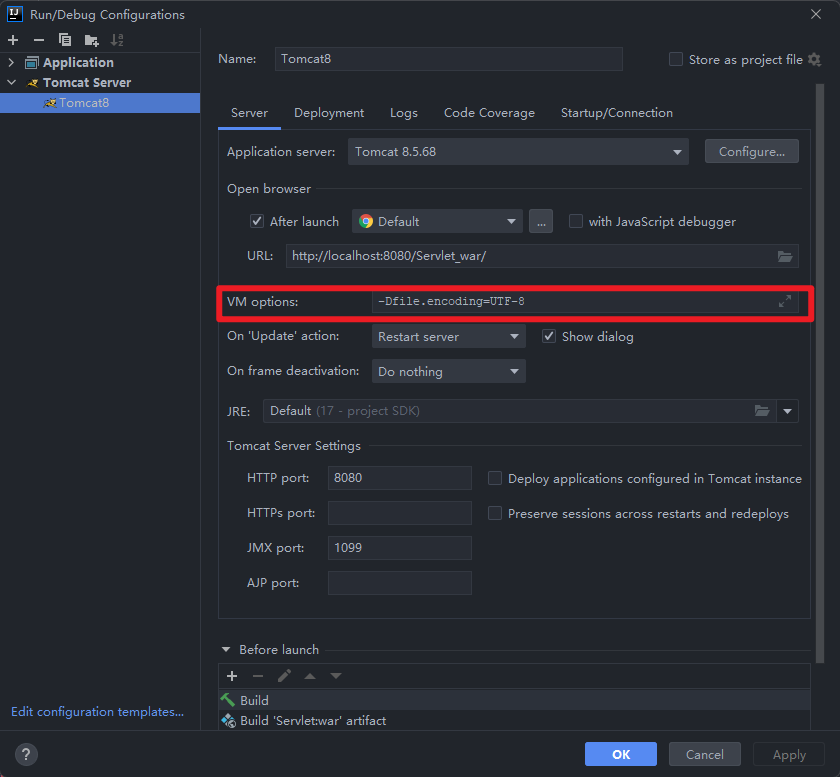
[Tomcat]解决IDEA中的Tomcat中文乱码问题
目录 1、IDEA 2、VM options 3、IDEA启动程序的存放目录 4、Tomcat 写在前面:此方法亲测有效!!! 1、IDEA 2、VM options 加上这两行: -Dfile.encodingUTF-8 -Dconsole.encodingUTF-8 3、IDEA启动程序的存放目录…...

python之dataclasses
一、场景 dataclasses模块提供了一种方便的方法来创建和管理数据对象 它可以帮助开发者更容易地创建简单的类,同时提供了一些实用的功能,例如自动实现__init__()、repr()、eq()等方法。 数据容器:如果您需要一个简单的类来存储一些数据&…...

【MapGIS精品教程】007:MapGIS投影变换案例教程
MapGIS投影变换,包括创建坐标系、定义投影、单点投影、类投影、批量投影。 文章目录 一、创建坐标系1. 创建高斯平面坐标系2. 创建阿尔伯斯投影二、定义投影三、投影变换1. 单点投影2. 类投影3. 批量投影一、创建坐标系 在MagGIS数据库中,有个空间参考系的文件夹,内置了常见…...

list数据根据属性字段去重
/*** 根据照片名称去重*/fun duplicateRemoval(list: MutableList<MediaBean>): MutableList<MediaBean>? {val mediaBeanList: MutableSet<MediaBean> if (Build.VERSION.SDK_INT > Build.VERSION_CODES.N) {TreeSet(Comparator.comparing(MediaBean::f…...
)
java教程(2023-3-8)
第一章:HelloWorld 1.java语言介绍 public class MainTest {public static void main(String[] args) { //软件分为系统软件和应用软件 //人机交互方式: 图形化界面 命令行方式/*常用的DOS命令:1.切换盘符:盘符 :2.创建文件夹m…...
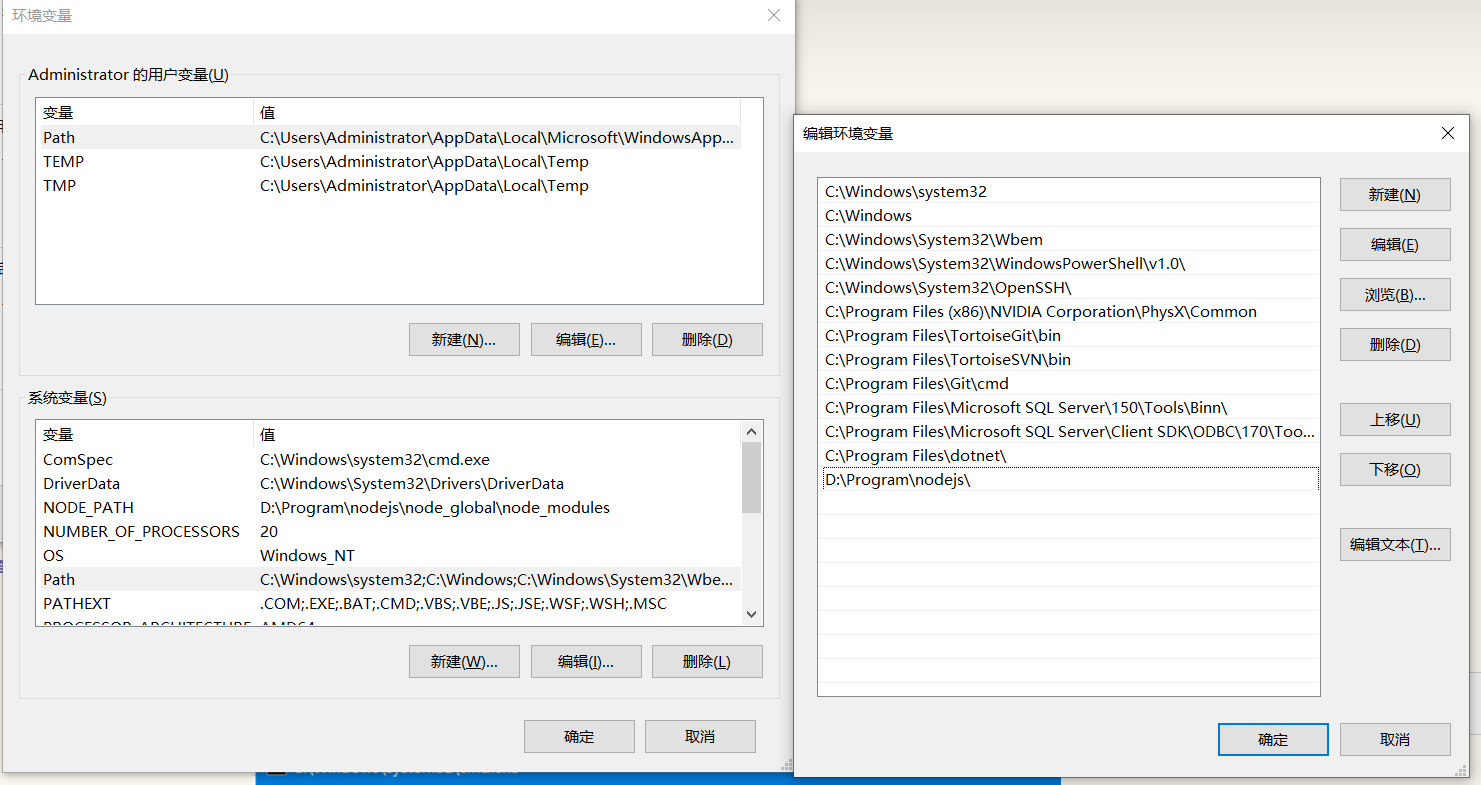
node 配置 vue npm配置
下载node 版本16https://nodejs.org/download/release/v16.16.0/node-v16.16.0-x64.msi复制安装地址,省空间,生报错老老实实复制就好D:\Program\nodejs新建node_cache和node_globalD:\Program\nodejs\node_cacheD:\Program\nodejs\node_global运行命令np…...

特斯拉、小鹏开路,城市NOA距好用还有几年?
作者 | Marshall 编辑 | 张祥威一项新技术,狂热的技术开发者往往会高估其发展速度,认为当下偶尔发生的安全问题,会随着数据积累和功能迭代被逐渐解决。 他们往往会说,“这个问题没有包含在我们的场景库中,但现在我们知…...

Vue 3第九章:WatchEffect高级侦听器
文章目录1. WatchEffect高级侦听器1.1. 使用 watchEffect 函数1.2. 停止侦听1.3. 侦听多个状态1.4. 懒执行总结1. WatchEffect高级侦听器 在 Vue 3 中,我们可以使用 watchEffect 函数来创建高级侦听器。与 watch 和 computed 不同,watchEffect 不需要指…...

c++基础——函数
函数的声明编程中的函数(function)一般是若干语句的集合。我们也可以将其称作“子过程(subroutine)”。在编程中,如果有一些重复的过程,我们可以将其提取出来,形成一个函数。函数可以接收若干值…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
