04-Fortran基础--Fortran数组和矩阵运算
04-Fortran基础--Fortran数组和矩阵运算

fortarn中对数组和矩阵的主要操作和内置运算包括:
-
数组的声明和初始化:fortarn中可以通过声明和初始化来创建数组。例如:integer :: my_array(3) = [1, 2, 3] ! 声明一个包含3个整数的数组并初始化 -
数组元素的访问:fortran中可以通过索引来访问数组中的元素。数组的索引从1开始。例如:my_array(2) = 5 ! 将数组中索引为2的元素设置为5 -
数组的赋值操作:fortran中可以使用等号将一个数组的值赋给另一个数组。例如:integer :: array1(3) = [1, 2, 3] integer :: array2(3) array2 = array1 ! 将array1的值赋给array2 -
数组的数学运算:fortran中可以对数组进行数学运算,例如加法、减法、乘法和除法。运算符会逐元素地应用于数组中对应的元素。例如:integer :: array1(3) = [1, 2, 3] integer :: array2(3) = [4, 5, 6] integer :: result(3)result = array1 + array2 ! 数组元素对应相加 -
数组的变形操作:fortran中可以通过reshape函数改变数组的形状。例如:integer :: old_array(6) = [1, 2, 3, 4, 5, 6] integer :: new_array(2, 3)new_array = reshape(old_array, [2, 3]) ! 将一维数组变形为二维数组 -
矩阵的运算:fortran中可以进行矩阵的乘法和转置运算。例如:real :: matrix1(2, 3) = reshape([1, 2, 3, 4, 5, 6], [2, 3]) real :: matrix2(3, 2) = reshape([7, 8, 9, 10, 11, 12], [3, 2]) real :: result(2, 2)result = matmul(matrix1, matrix2) ! 矩阵乘法 result = transpose(matrix1) ! 矩阵转置
以上是fortran中对数组和矩阵的主要操作和内置运算的一些示例。实际使用时,还可以进行更多的操作,例如数组的排序、矩阵的求逆等。😃
相关文章:

04-Fortran基础--Fortran数组和矩阵运算
04-Fortran基础--Fortran数组和矩阵运算 fortarn中对数组和矩阵的主要操作和内置运算包括: 数组的声明和初始化:fortarn中可以通过声明和初始化来创建数组。例如: integer :: my_array(3) [1, 2, 3] ! 声明一个包含3个整数的数组并初始化数…...
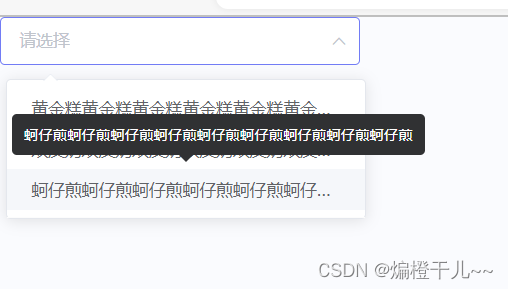
el-select选项框内容过长
利用popper-class实现选项框内容过长,截取显示功能: <el-select popper-class"popper-class" :popper-append-to-body"false" v-model"value" placeholder"请选择"><el-optionv-for"item in opt…...

K8S面试题学习5
参考K8S面试题(史上最全 持续更新)_kubernetes常见面试题-CSDN博客做的个人总结,规划是每天看10题,thx! 1. 请详述kube-proxy原理? 每个node节点都会运行一个kube-proxy的进程,核心功能是将service的访问…...
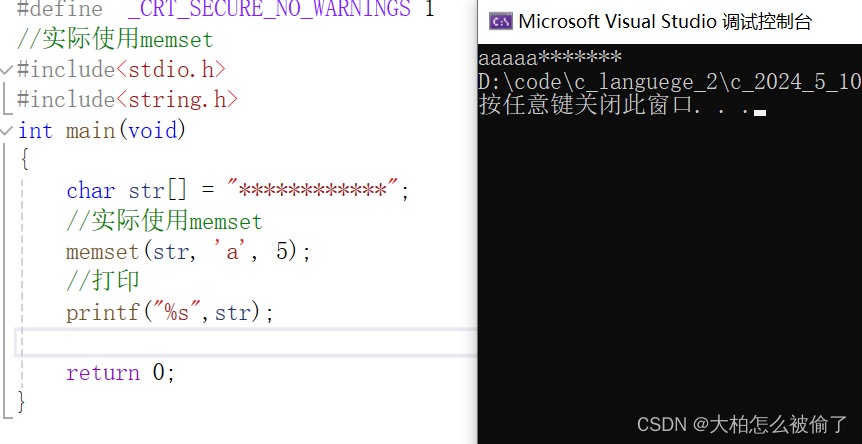
字符以及字符串函数
字符以及字符串函数 求字符串长度strlen 长度不受限制的字符串函数strcpystrcatstrcmp 长度受限制的字符串函数strncpystrncatstrncmp 字符串查找strstrstrtok 错误信息报告strerror 字符分类函数字符转换函数tolowertoupper 内存操作函数memcpymemmovememcmpmemset 这篇文章注…...

记录解决问题--redis ssl连接
1.问题场景 springboot连接redis启动报错,感觉是没连上redis,本地是正常启动的,但是本地不是ssl连接。 2.redis ssl连接知识 ①一般不开启ssl的连接,直接连接即可,有密码输密码。 ②不受信的ssl连接,也就…...

买卖股票的最佳时机
dp[i][0] 表示第i天持有股票所得最多现金,相当于买的价格最低,卖的价格最高 持有股票状态为0,不持有为1 用二维数组表示天数和是否持有, i-1天就持有,或者第i天买入 class Solution {public int maxProfit(int[] p…...

Linux部署安装
Linux部署安装 Linux中有两种软件安装包 一、源码包 软件的源代码是软件的原始数据,但是源代码不能直接在计算机中直接运行安装。 需要通过编译将源代码转换为计算机可以识别的机器语言,之后才可以进行安装。 源码包安装的方式可以在安装过程中发根据…...

docker搭建mysql集群实现主从复制
前言 随着业务的增长,一台数据服务器已经满足不了需求了,负载过重。这个时候就需要减压了,实现负载均衡和读写分离,一主一丛或一主多从。 主服务器只负责写,而从服务器只负责读,从而提高了效率减轻压力。 …...
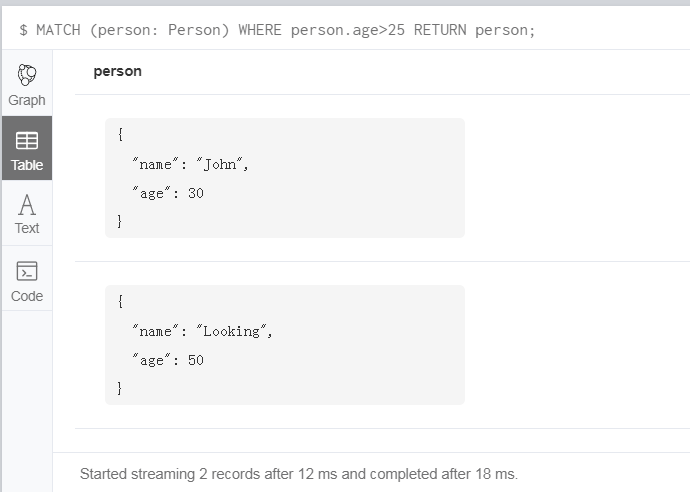
Neo4j 之安装和 CQL 基本命令学习
正常使用结构化的查询语言 SQL(Structured Query Language)较多一些,但是像 Neo4j 这种非结构化的图形数据库来说,就不得不学习下 CQL(Cypher Query Language)语言了。如果你之前学过 《离散数学》或《图论…...
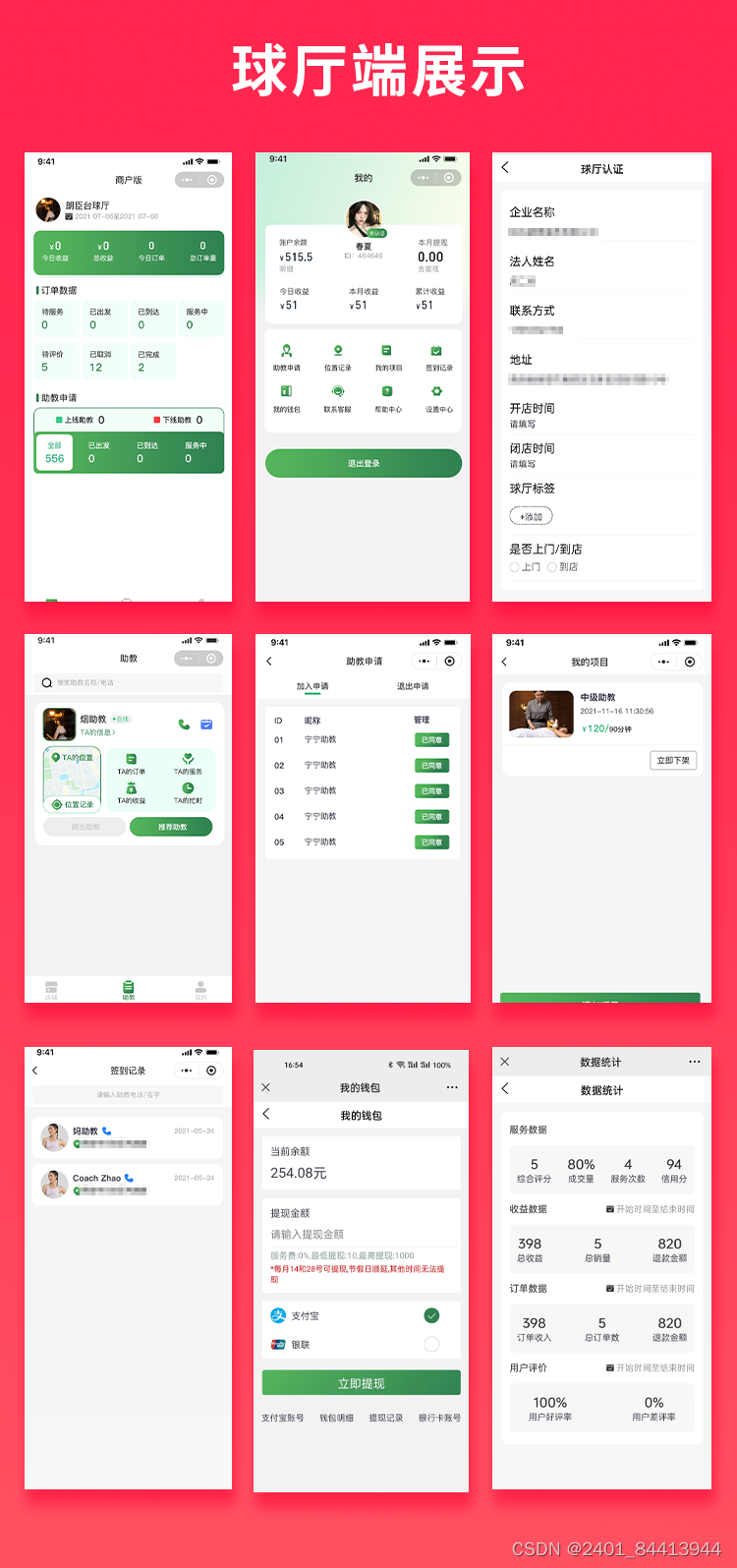
【全开源】JAVA台球助教台球教练多端系统源码支持微信小程序+微信公众号+H5+APP
功能介绍 球厅端:球厅认证、教练人数、教练的位置记录、助教申请、我的项目、签到记录、我的钱包、数据统计 教练端:我的页面,数据统计、订单详情、保证金、实名认证、服务管理、紧急求助、签到功能 用户端:精准分类、我的助教…...

机器学习-如何为模型选择评估指标?
为机器学习模型选择评估指标是一个关键步骤,因为它直接关联到如何衡量模型的性能。以下是选择评估指标的一些建议: 1、理解问题类型: 分类问题:对于二分类问题,常见的评估指标包括准确率、精确率、召回率、F1分数、R…...

【AutoGPT】踩坑帖(follow李鱼皮)
本文写于2024年5月7日 参考视频:AutoGPT傻瓜式使用教程真实体验! 对应文章:炸裂的AutoGPT,帮我做了个网站! 平台:GitPod 云托管服务 原仓库已经改动很大,应使用的Repo为:Auto-GPT-ZH…...

机器学习-L1正则/L2正则
机器学习-L1正则/L2正则 目录 1.L1正则 2.L2正则 3.结合 1.L1正则 L1正则是一种用来约束模型参数的技术,常用于机器学习和统计建模中,特别是在处理特征选择问题时非常有用。 想象一下,你在装备行囊准备去旅行,但你的行囊有一…...
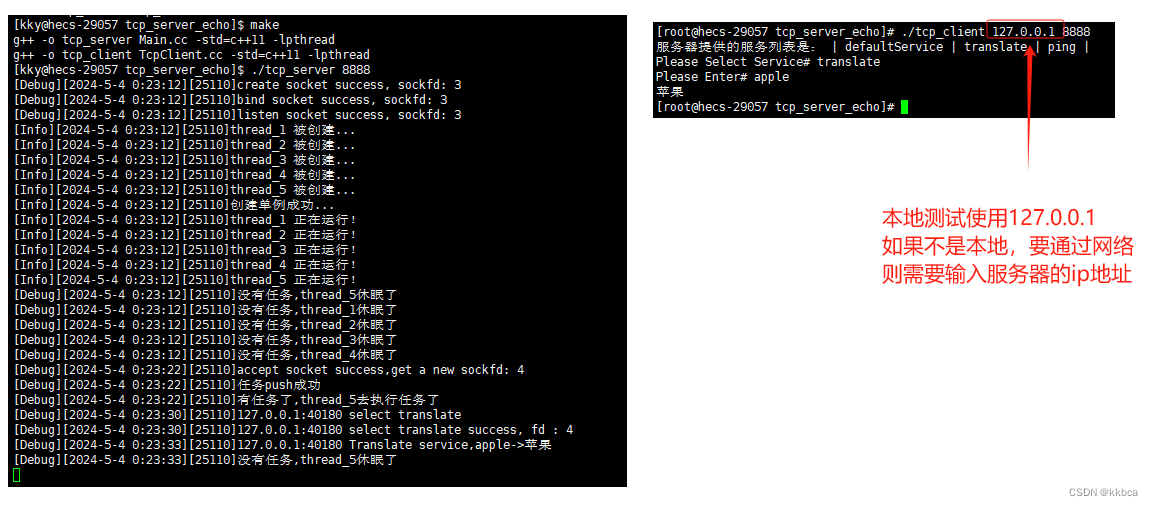
Linux——socket编程之tcp通信
前言 前面我们学习socket的udp通信,了解到了socket的概念与udp的实现方法,今天我们来学习一下面向连接的tcp通信。 一、tcp套接字创建 UDP和TCP都是通过套接字(socket)来实现通信的,因此TCP也得使用socket()接口创建…...

HTTP协议介绍
文章目录 http协议http协议格式GET请求POST请求http客户端实现 http协议 http协议是应用层协议,一般建立在tcp协议的基础之上(当然你的实现非要基于udp也是可以的),也就是说http协议的数据收发是通过tcp协议的。 http协议也分为h…...

elasticsearch安装配置注意事项
安装Elasticsearch时,需要注意以下几个重要事项: 1、版本选择:选择与你系统和其他组件(如Logstash、Kibana)兼容的Elasticsearch版本。 2、Java环境:Elasticsearch是基于Java构建的,因此确保已…...
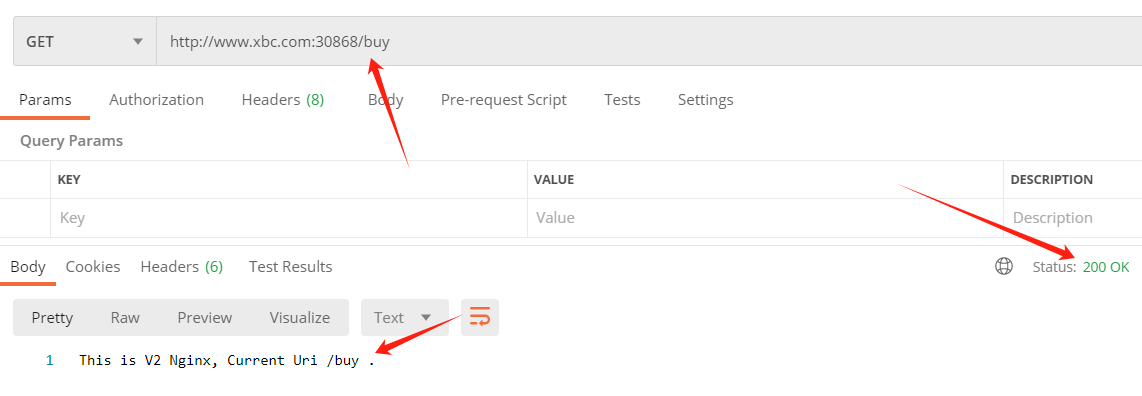
Istio 流量管理(请求路由、流量转移、请求重试、流量镜像、故障注入、熔断等)介绍及使用
一、Istio 流量管理 Istio是一个开源的服务网格,它为分布式微服务架构提供了网络层的抽象。它使得服务之间的通信变得更为可靠、安全,并且提供了细粒度的流量管理、监控和策略实施功能。Istio通过在服务之间插入一个透明的代理(Envoy&#x…...

Transformers中加载预训练模型的过程剖析
使用HuggingFace的Transformers库加载预训练模型来处理下游深度学习任务很是方便,然而加载预训练模型的方法多种多样且过程比较隐蔽,这在一定程度上会给人带来困惑。因此,本篇文章主要讲一下使用不同方法加载本地预训练模型的区别、加载预训练模型及其配置的过程,藉此做个记…...

使用MCU的 GPIO口 模拟SDIO时序读写TF/SD卡的可能性。
SD2.0协议详解:命令格式、初始化/读取/写入 - WangXuan的文章 - 知乎 https://zhuanlan.zhihu.com/p/610495260 参考上述与其它理解,若使用GPIO口模拟,重点与难点: 1. 时钟线问题: 在SD准备期间,需不间断…...
SSM【Spring SpringMVC Mybatis】——Mybatis(二)
如果对一些基础理论感兴趣可以看这一期👇 SSM【Spring SpringMVC Mybatis】——Mybatis 目录 1、Mybatis中参数传递问题 1.1 单个普通参数 1.2 多个普通参数 1.3 命名参数 1.4 POJO参数 1.5 Map参数 1.6 Collection|List|Array等参数 2、Mybatis参数传递【#与…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
