Codeforces Round 134 (Div. 1) A. Ice Skating (并查集)
Ice Skating
题面翻译
Description
给出n个点的横纵坐标,两个点互通当且仅当两个点有相同的横坐标或纵坐标,问最少需要加几个点才能使得所有点都两两互通
Input
第一行一个整数n表示点数,之后n行每行两个整数x[ i ]和y[ i ]表示第i个点的横纵坐标(1<=n<=100,1<=x[ i ],y[ i ]<=1000)
Output
输出需要加的最少点数
题目描述
Bajtek is learning to skate on ice. He’s a beginner, so his only mode of transportation is pushing off from a snow drift to the north, east, south or west and sliding until he lands in another snow drift. He has noticed that in this way it’s impossible to get from some snow drifts to some other by any sequence of moves. He now wants to heap up some additional snow drifts, so that he can get from any snow drift to any other one. He asked you to find the minimal number of snow drifts that need to be created.
We assume that Bajtek can only heap up snow drifts at integer coordinates.
输入格式
The first line of input contains a single integer $ n $ ( $ 1<=n<=100 $ ) — the number of snow drifts. Each of the following $ n $ lines contains two integers $ x_{i} $ and $ y_{i} $ ( $ 1<=x_{i},y_{i}<=1000 $ ) — the coordinates of the $ i $ -th snow drift.
Note that the north direction coinсides with the direction of $ Oy $ axis, so the east direction coinсides with the direction of the $ Ox $ axis. All snow drift’s locations are distinct.
输出格式
Output the minimal number of snow drifts that need to be created in order for Bajtek to be able to reach any snow drift from any other one.
样例 #1
样例输入 #1
2
2 1
1 2
样例输出 #1
1
样例 #2
样例输入 #2
2
2 1
4 1
样例输出 #2
0
使用并查集求解。
首先应明确,在这道题中,想要连接任意两堆雪,只需要增加一堆雪就可以。
然后我们想在想要知道应该增加几堆雪,就只需要知道有几堆雪没有连接起来,没有连接的雪的数量减一就是需要增加的雪堆的数量。
那么只需要枚举所有的点,然后使用并查集合并上所有能够在同一个横轴或者纵轴的点,最后求解出来连通块的数量,就能够得到没有连通的数量。
CODE:
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
#define pii pair<int,int>
#define x first
#define y secondint p[N];
int n;
pii a[N];int find(int x){if(x != p[x])p[x] = find(p[x]);return p[x];
}int main(){cin >> n;for(int i = 1;i <= n;i++)cin >> a[i].x >> a[i].y;for(int i = 0;i < N;i++)p[i] = i;for(int i = 1;i <= n;i++){for(int j = i + 1;j <= n;j++){if(a[i].x == a[j].x || a[i].y == a[j].y){p[find(i)] = find(j);}}}int cnt = 0;for(int i = 1;i <= n;i++)if(p[i] == i)cnt++;cout << cnt - 1 << endl;return 0;
}
相关文章:
 A. Ice Skating (并查集))
Codeforces Round 134 (Div. 1) A. Ice Skating (并查集)
Ice Skating 题面翻译 Description 给出n个点的横纵坐标,两个点互通当且仅当两个点有相同的横坐标或纵坐标,问最少需要加几个点才能使得所有点都两两互通 Input 第一行一个整数n表示点数,之后n行每行两个整数x[ i ]和y[ i ]表示第i个点的…...

深入了解 Flask Request
文章目录 获取请求数据获取请求信息文件上传总结 Flask 是一个轻量级的 Python Web 框架,其简洁的设计和灵活的扩展性使其成为了许多开发者的首选。在 Flask 中,处理 HTTP 请求是至关重要的,而 Flask 提供了丰富而强大的 request 对象来处理…...

前端测试策略与实践:单元测试、E2E测试与可访问性审计
前端测试策略是确保Web应用程序质量、性能和用户体验的关键组成部分。有效的测试策略通常包括单元测试、端到端(E2E)测试以及可访问性审计等多个层面。以下是关于这三类测试的策略与实践建议: 单元测试 定义与目的: 单元测试是针…...

修改el-checkbox样式
一定要在最外层; //未选中框/deep/ .el-checkbox__inner{border-color: #0862a3;}//选中框/deep/ .el-checkbox__input.is-checked .el-checkbox__inner{background-color: #0862a3;border-color: #0862a3;}//未选中框时右侧文字/deep/ .el-checkbox__label{}//选中…...

UE5缺少SDK,而无法在windows平台打包的解决方法
问题1:UE5缺少SDK,而无法在windows平台打包的解决方法(项目问题,做一下记录,没有参考性) (1)打不开:D:\imageworks-OpenColorIO-Configs-v1.0_r2-8-g0bb079c.tar 解决方案:从23拷贝D…...
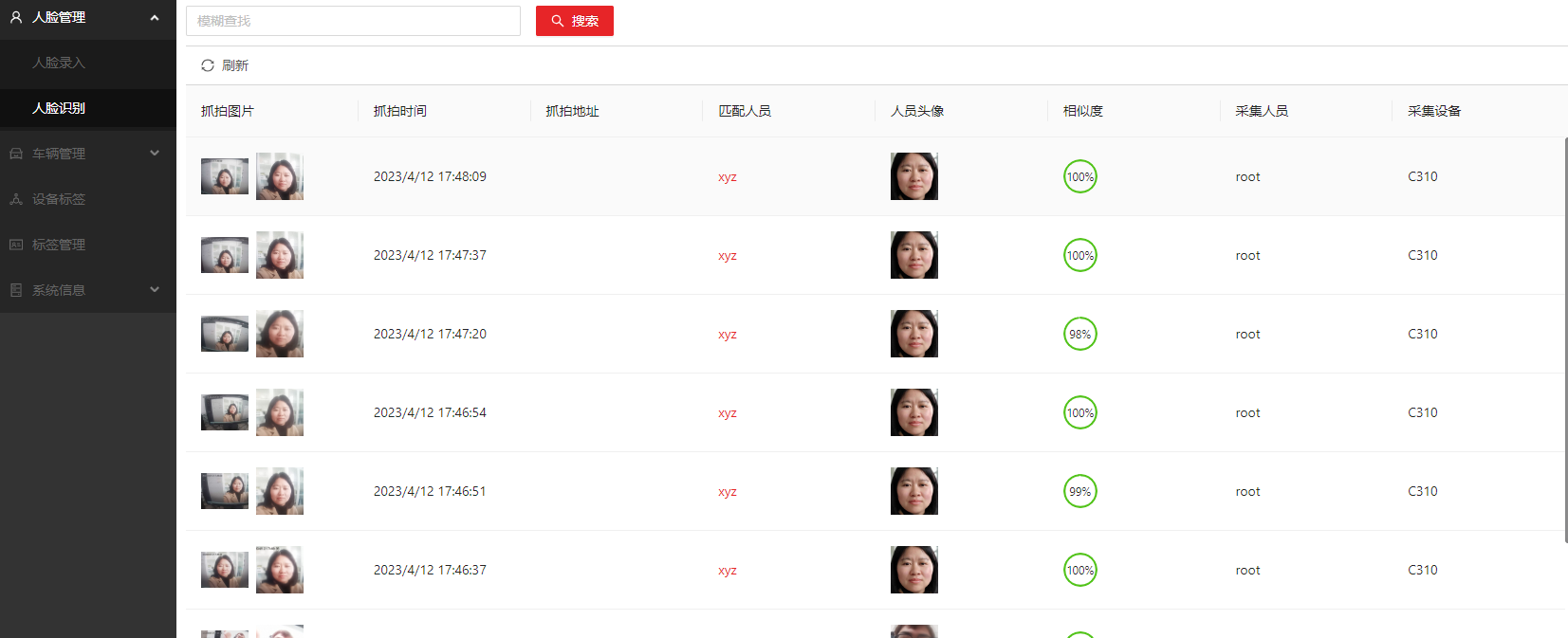
4G,5G执法记录仪人脸识别、人脸比对使用说明
4G/5G执法记录仪或4G/5G智能安全帽,做前端人脸识别、人脸比对,采用了上市公司的成熟的人脸识别算法,需要支付LICENSE给算法公司,理论上前端设备支持30K的人脸库(受设备运行内存限制)。 4G/5G执法记录仪侧要…...
掌握SEO优化的关键:提升网站排名的秘籍(如何提高网站seo排名)
你是否曾经在搜索引擎上搜索过一个关键词,然后点击了排在前几位的网站?如果是,那么你已经体会到了SEO(搜索引擎优化)的威力。SEO是一项关键的网络营销策略,它能够让你的网站在搜索引擎中获得更高的排名&…...

大模型微调之 在亚马逊AWS上实战LlaMA案例(九)
大模型微调之 在亚马逊AWS上实战LlaMA案例(九) 代码阅读 src/llama_recipes/inference/prompt_format_utils.py 这段代码是一个Python模块,它定义了几个类和模板,用于生成安全评估的提示文本。以下是对每一行代码的注释和提示词…...

Php php7的特性
1. 性能优化 PHP7引入了Zend Engine 3.0,显著提高了执行效率,相比PHP 5.x,性能提升了2-3倍。这个特性无法直接通过代码示例展示,但你可以感受到在升级到PHP7后,相同代码的执行速度更快。 2. 函数返回类型声明 允许在…...
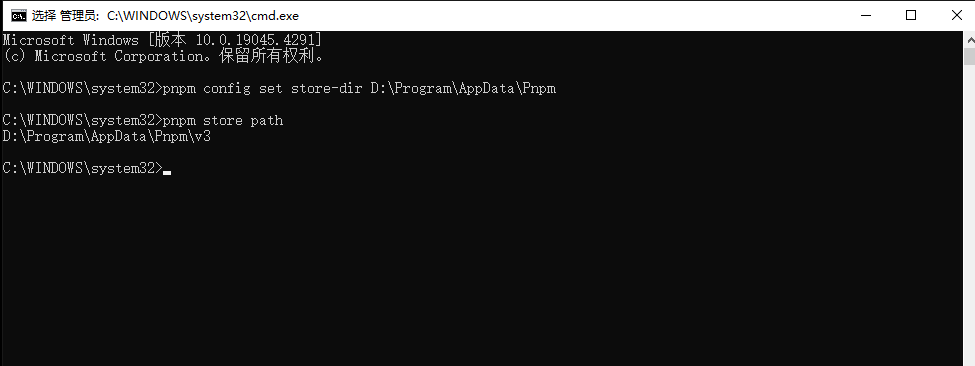
node pnpm修改默认包的存储路径
pnpm与npm的区别 PNPM和NPM是两个不同的包管理工具。 NPM(Node Package Manager)是Node.js的官方包管理工具,用于安装、发布和管理Node.js模块。NPM将包安装在项目的node_modules目录中,每个包都有自己的依赖树。 PNPM…...
Adobe-Premiere-CEP 扩展 入门-视频剪辑-去气口插件-Silence Remover
短视频,这两年比较火,不要再问为什么用Premiere,非常难用,为什么不用某影,某些国内软件非常接地气简单,又例如某音资深的视频短编辑就很好用了。。。 Premiere二次开发调试难,不如自己搞个cons…...

基于多目标灰狼算法的冷热电联供型微网低碳经济调度
针对冷热电联供型微电网运行调度的优化问题,为实现节能减排的目标,以微电网运行费用和环境污 染成本为优化目标,建立了包含风机、微型燃气轮机、余热锅炉、溴化锂吸收式制冷机等微源的微电网优化 模型。模型的优化求解使用改进的多目标灰狼优化算法,得到多目标问题的 Paret…...
 和 (?<=...) 符号)
Python 正则表达式 (?=...) 和 (?<=...) 符号
Python 正则表达式 引言正文示例1示例2示例3示例4 引言 今天遇到了一个比较棘手的问题,于是终于打算要对正则表达式中的 (?...) 和 (?<...) 符号动手了。 正文 (?...) 表示当 … 匹配时,匹配成功,但不消耗字符串中的任何字符。这个…...

Vue.js中使用JavaScript实现路由跳转详解
在Vue应用中,利用Vue Router进行页面间的导航是一个常见需求。本篇博客将通过示例代码详细介绍如何在Vue组件中使用JavaScript实现路由跳转,包括传递参数的两种方式:通过params和query。让我们一步步深入了解。 基础设置 首先,确…...

社群裂变:从微光到星火的社群增长奥秘
在当今社交媒体盛行的时代,社群裂变已成为众多品牌、企业和个人实现快速增长的重要策略。社群裂变不仅能够有效扩大影响力,还能精准触达目标用户,实现高效转化。本文将深入探讨社群裂变的内涵、策略及实施方法,助您揭开社群增长的…...
Git命令Gitee注册idea操作git超详细
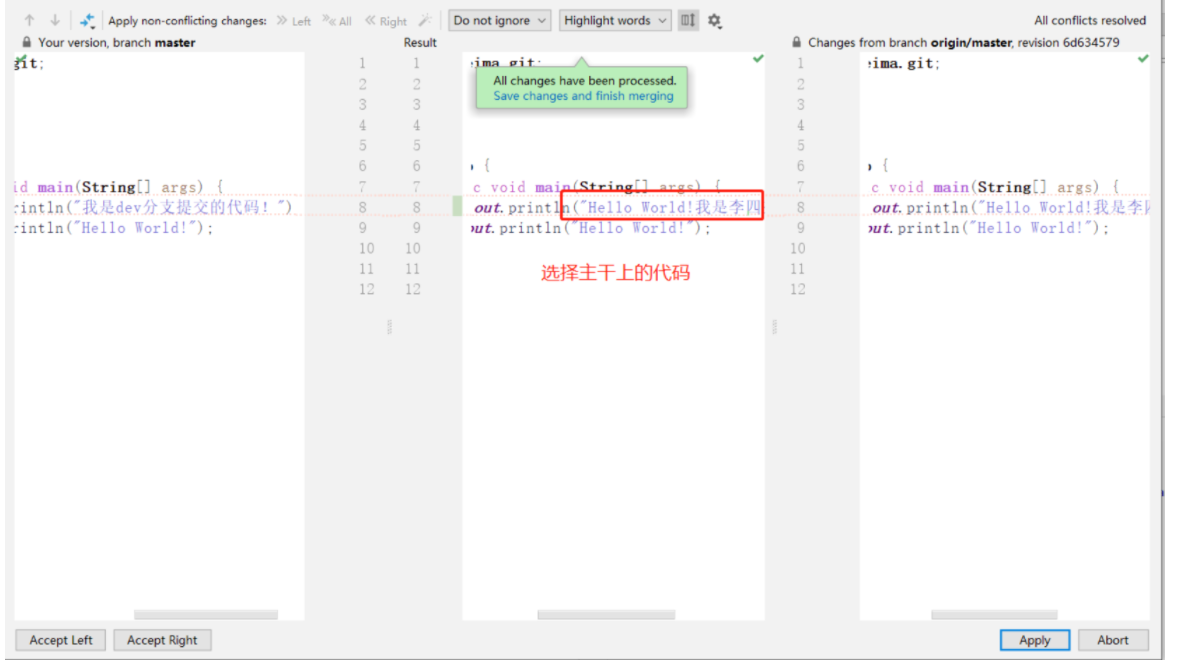
文章目录 概述相关概念下载和安装常见命令远程仓库介绍与码云注册创建介绍码云注册远程仓库操作关联拉取推送克隆 在idea中使用git集成add和commit差异化比较&查看提交记录版本回退及撤销与远程仓库关联 push从远程仓库上拉取,克隆项目到本地创建分支切换分支将…...

出差行程到底怎么管?这个“高分指南”划重点来了!
在日常商旅过程中,出差行程计划是必不可少的环节。公司需要以此为依据判断行程是否有必要、是否合理,确保出差行程与公司的业务需求相符。 通过胜意费控云,员工填写出差申请时,行程计划智能生成,平台自动匹配并带出差标…...

js设计模式--发布订阅者模式
概述 发布订阅者模式用于处理对象之间的事件通信,该模式涉及两个主要角色:发布者(Publisher)和订阅者(Subscriber) 发布者维护一个事件列表,并在事件发生时通知所有已注册的订阅者。订阅者可以…...

【图论】图论基础
图论不同地方讲的不太一样,本文仅限作者的理解 定义 图一般由点集 V V V 和边集 E E E 组成。 对于 v ∈ V v\in V v∈V,称 v v v 为该图的一个节点。 对于 e ∈ E e\in E e∈E,一般用二元组 ( u , v ) (u,v) (u,v) 表示 e e e&…...
Konga域名配置多个路由
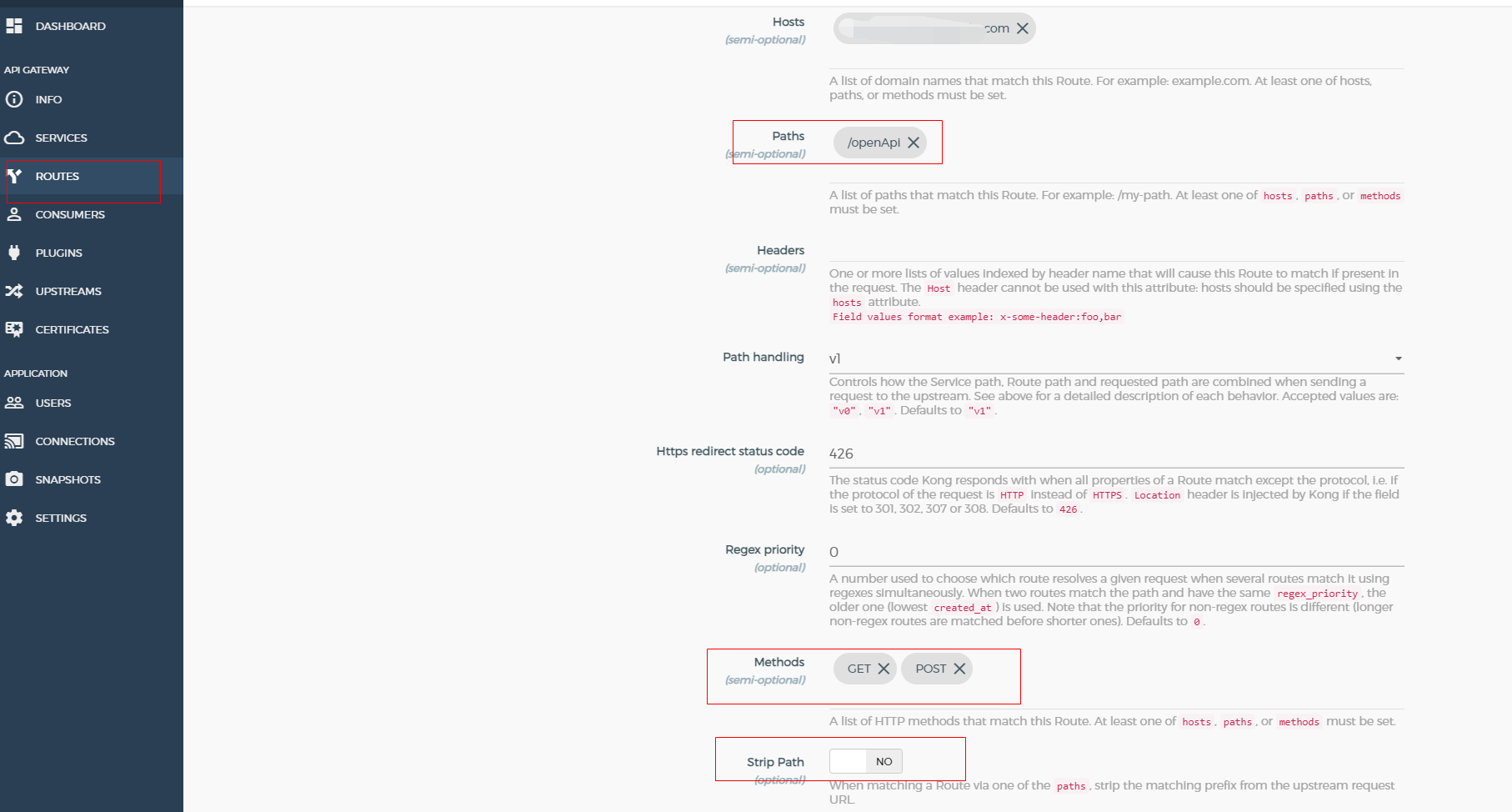
云原生API网关-Kong部署与konga基本使用 Nginx server{listen 443 ssl;location / {proxy_pass http://127.0.0.1:8100;}location /openApi {proxy_pass http://172.31.233.35:7100/openApi;} } Kong {"id": "f880b21c-f7e0-43d7-a2a9-221fe86d9231&q…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
