【图论】图论基础
图论不同地方讲的不太一样,本文仅限作者的理解
定义
图一般由点集 V V V 和边集 E E E 组成。
对于 v ∈ V v\in V v∈V,称 v v v 为该图的一个节点。
对于 e ∈ E e\in E e∈E,一般用二元组 ( u , v ) (u,v) (u,v) 表示 e e e,其中 u , v ∈ V u,v\in V u,v∈V。在无向图中,该二元组无序,即边为双向;在有向图中,该二元组有序,即边为单向。
一个带有边权(边的长度)的图称为带权图,此时边一般记为 ( u , v , w ) (u,v,w) (u,v,w)。
下面分别是一个无向图和一个有向图的例子:


连通性
从一个图中选出一些节点和边,构成一个合法的新图,称做原图的子图。
扩展至最大的符合某一要求的子图被称为分量。
通过图中的边可以使节点之间联通(单向联通也算)的图称做连通图。
节点之间两两可以互相到达的有向图被称做强联通图。
如果一个图中某一个点及其边被删去后,图将不再联通,则称该点为原图的一个割点。
没有割点的图被称为点双连通图。
如果一个图中某一条边被删去后,图将不再联通,则称该边为原图的一个割边。
没有割边的图被称为边双连通图。
读者可以自行理解联通子图、联通分量、强连通子图、强连通分量、点双联通子图、点双联通分量、边双联通子图、边双联通分量等概念。
树与环
一个没有环的图称为无环图。
一个没有环的有向图称为有向无环图(DAG)。
一个没有环且联通的无向图称为树。
一个有恰一个环且联通的无向图称为基环树。
一个是树且包含所有节点的子图称为原图的生成树。
存储
一般有两种存储方式,邻接矩阵和邻接表。
邻接矩阵
使用一个矩阵来存储图,对于矩阵中的一个元素 G u , v G_{u,v} Gu,v:
在无权图中, u , v u,v u,v 之间有边为 1 1 1,无边为 0 0 0;
在带权图中, u , v u,v u,v 之间有边为 w w w,无边为 inf \inf inf。
邻接表
使用多个数组来存储图,对于每一个数组 G u G_u Gu
在无权图中, u , v u,v u,v 间有边则加入 v v v;
在带权图中, u , v u,v u,v 间有边则加入有序二元组 ( v , w ) (v,w) (v,w)。
代码
分为定义,输入和遍历三部分
- 邻接矩阵
int G[N][N];
memset(G,0,sizeof(G));//无权
memset(G,INF,sizeof(G));//带权
for (int i=1;i<=m;i++){//无权int u,v;cin>>u>>v;G[u][v]=1;G[v][u]=1;//仅限无向图//带权int u,v,w;cin>>u>>v>>w;G[u][v]=w;G[v][u]=w;//仅限无向图
}
for (int u=1;u<=n;u++) for (int v=1;v<=n;v++)if (G[u][v])//无权if (G{u][v]!=INF)//带权
- 邻接表
vector<int> G[N];//无权
//带权
struct edge{int v,w;};
vector<edge> G[N];
for (int i=1;i<=m;i++){//无权int u,v;cin>>u>>v;G[u].push_back(v);G[v].push_back(u);//仅限无向图//带权int u,v,w;cin>>u>>v>>w;G[u].push_back({v,w});G[v].push_back({u,w});//仅限无向图
}
for (int u=1;u<=n;u++)for (int v:G[u])//无权for (edge e:G[u])//带权
相关文章:

【图论】图论基础
图论不同地方讲的不太一样,本文仅限作者的理解 定义 图一般由点集 V V V 和边集 E E E 组成。 对于 v ∈ V v\in V v∈V,称 v v v 为该图的一个节点。 对于 e ∈ E e\in E e∈E,一般用二元组 ( u , v ) (u,v) (u,v) 表示 e e e&…...
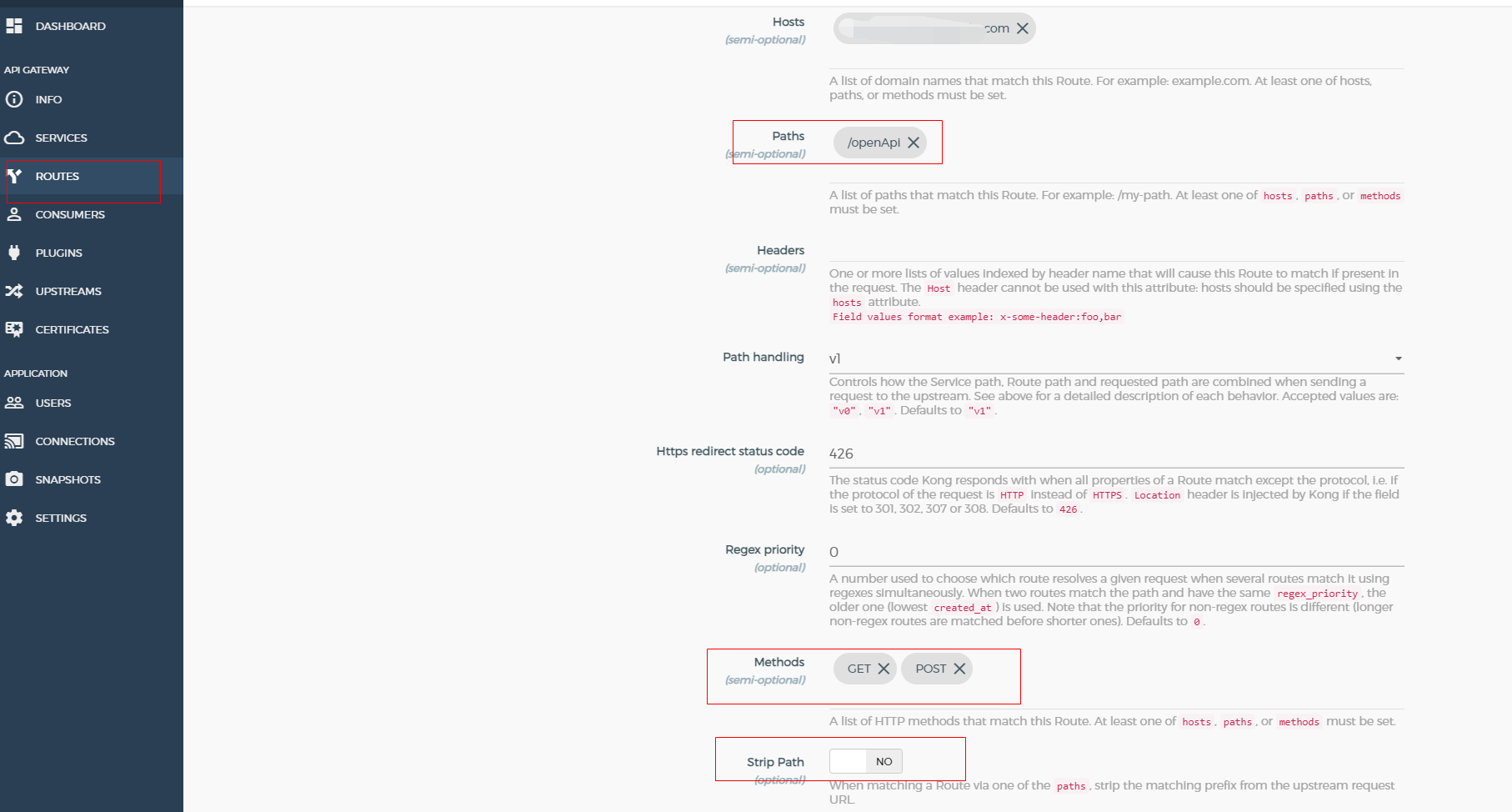
Konga域名配置多个路由
云原生API网关-Kong部署与konga基本使用 Nginx server{listen 443 ssl;location / {proxy_pass http://127.0.0.1:8100;}location /openApi {proxy_pass http://172.31.233.35:7100/openApi;} } Kong {"id": "f880b21c-f7e0-43d7-a2a9-221fe86d9231&q…...

15.计算机网络
1.物理层的互联设备 中继器 和 集线器 2.集线器可以看做特殊的多路中继器 集线器 不可以做到自动寻址的功能 3.数据链路层 网桥 和 交换机 4.交换机是多端口网桥 5.网络层 路由器 6.应用层 网关 7.广播域 网络层 可以形成多个广播域 冲突域 网络层数据链路层 可以形成多个冲突域…...

【大数据·hadoop】在hdfs上运行shell基本常用命令
一、准备工作 1.1格式化并启动Hadoop服务 参见Hadoop在ubuntu虚拟机上的伪分布式部署|保姆级教程的4.7节 二、HDFS常用命令 接着,就愉快地在刚刚的命令行里敲命令啦 1.显示hdfs目录结构 hadoop fs -ls -R /hadoop fs: 这是Hadoop文件系统命令行的一部分&#x…...

TCP/IP 协议基础:构建互联网基石
目录 前言 一.网络通信协议 TCP/IP 1.网络通信协议 3.TCP/IP 协议 3.管理的组织和机构 4.RFC 二.OSI 参考模型 1.层次结构 2.通信机制 3.PDU 4.各层的功能 三.TCP/IP 协议簇 1.TCP/IP 与 OSI 的对应关系 2.TCP/IP 各层 3.TCP/IP 封装与分用 4.重要概念 5.分…...
高通OMX组件实现基础)
Android OpenMAX(三)高通OMX组件实现基础
上一节了解了OMX组件实现的基础内容,这一节我们以高通OMX实现为例,简单看看如何实现一个OMX组件。本节代码参考自: omx_core_cmp.cpp qc_omx_component.h omx_vdec.h omx_vdec.cpp Tips:本篇文章旨在简单了解如何实现一个OMX组件,细节的内容不会仔细解读,代码阅读跳跃幅度…...

【比邻智选】MF871U模组
🚀搭载国产芯,严苛测试,稳定可靠 🛠️R16特性加持,5G LAN,纳秒级精度 🌐超低成本,丰富协议,连接无界限...

Unity 单例模式
Unity中单例模式是非常常用的写法,可以基于C#语言的几种不同方法来实现。 下面我将列出几种常见的实现方式: 1. 经典的单例模式 public class SingletonExample : MonoBehaviour {private static SingletonExample instance;public static SingletonEx…...
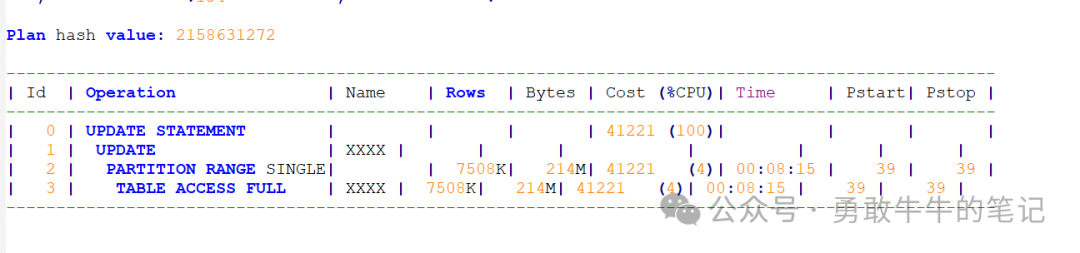
Oracle-一次TX行锁堵塞事件
问题背景: 接用户问题报障,应用服务出现大量会话堆积现象,数据库锁堵塞严重,需要协助进行问题定位和排除。 问题分析: 登录到数据库服务器上,首先查看一下数据库当前的等待事件情况,通过gv$ses…...

Gtid方式搭建主从复制+MHA高可用集群
GTID是什么 GTID(全局事务标识符),它用于唯一标识一个事务。每个GTID由三个部分组成: 服务器唯一标识符事务序列号全局事务标识符使用gtid可以简化主从复制的配置和管理,减少由于复制链路终端、主从数据不一致等问题带来的风险如何开启GTID: 在/etc/my.cnf文件中添加如下…...
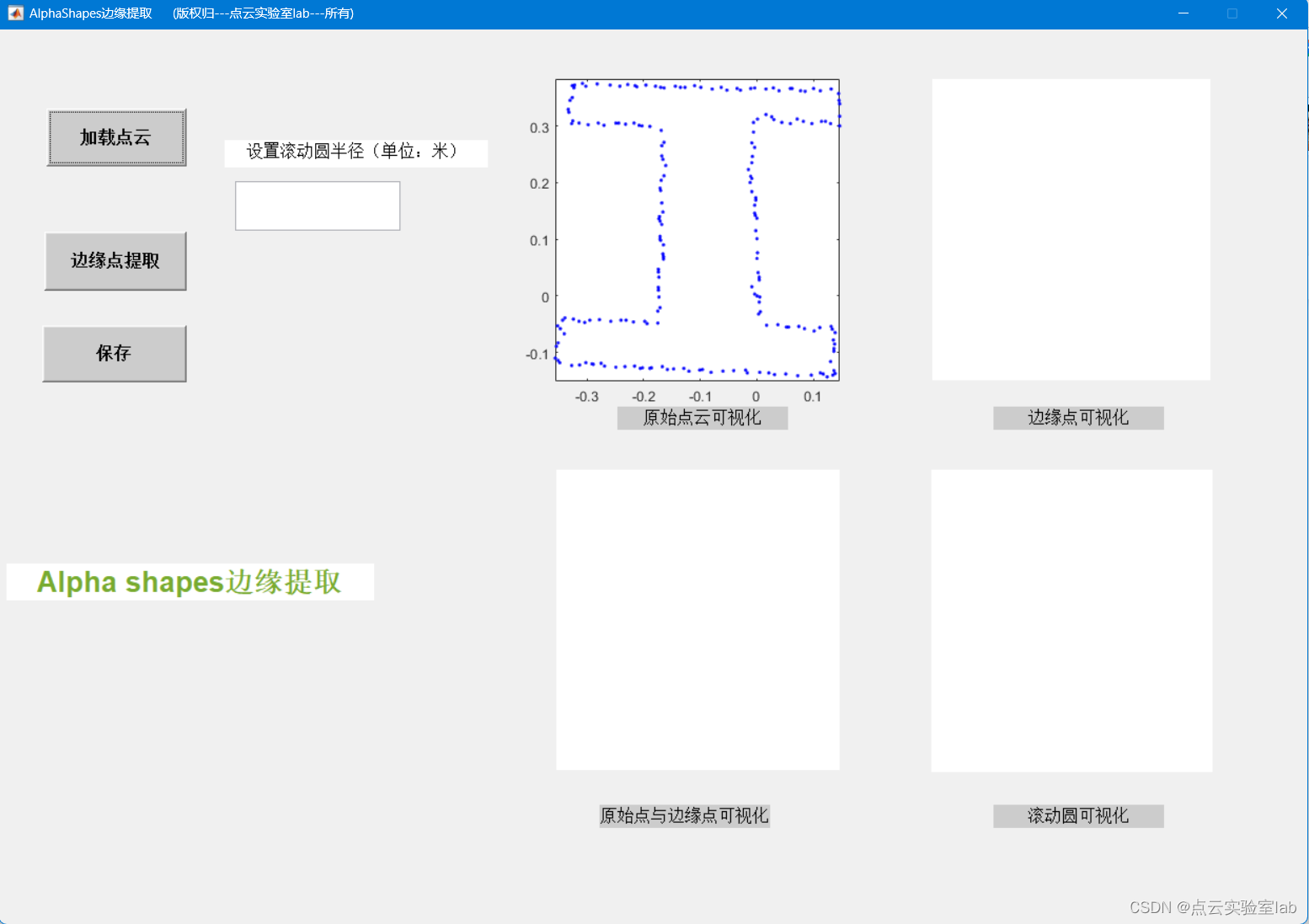
基于matlab GUI的Alpha shapes边缘提取
1、程序介绍 本程序是基于matlab语言,使用alpha shapes算法实现点云边缘提取。算法具体原理参考博客:基于alpha shapes的边缘点提取(matlab)-CSDN博客。该程序包括3个按钮:加载点云、边缘点提取、保存。其中࿰…...

[Android]常见的包管理方式
在Android开发中,包管理主要是通过构建和依赖管理工具来处理。下面列举了几种最常见和主流的包管理方式: 一、Gradle Gradle 是 Android 官方推荐的构建工具,几乎成为了 Android 开发的标准。它支持自定义构建逻辑、依赖管理、多项目构建等…...

每日10亿数据的日志分析系统OOM
背景 一个每日10亿数据的日志清洗系统,主要工作就是从消息队列中消费各种各样的日志,然后对日志进行清洗,例如:用户敏感信息(姓名、手机号、身份证)进行脱敏处理,然后把清理完的数据交付给其他系统使用。 我们项目中,…...

智能驱动,精准管理:打造高效干部管理系统
干部管理系统是现代组织管理中不可或缺的工具,它通过信息技术的应用,提高了干部管理的效率和准确性。干部管理系统的主要功能包括: 1. 信息管理:系统可以存储和管理干部的个人信息,包括基本资料、工作经历、教育背景、…...
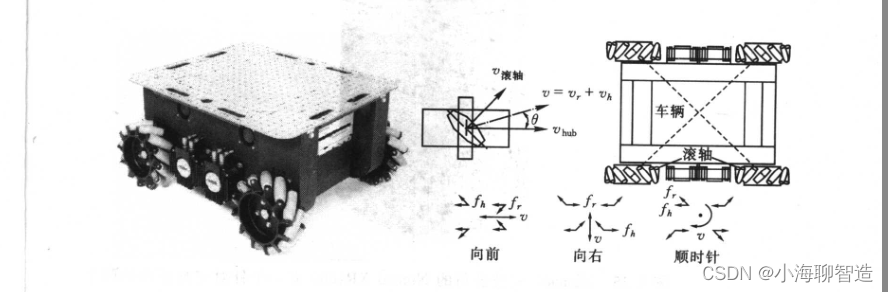
轮式机器人简介
迄今为止,轮子一般是移动机器人学和人造交通车辆中最流行的运动机构。它可达到很高的效率, 如图所示, 而且用比较简单的机械就可实现它的制作。 另外,在轮式机器人设计中,平衡通常不是一个研究问题。 因为在所有时间里,轮式机器人一般都被设计成在任何时间里所有轮子均与地接…...

已知哈夫曼节点个数,求哈夫曼字符编码数
哈夫曼编码(Huffman Coding)是一种用于无损数据压缩的嫡编码(权编码)算法。 在哈夫曼树中,每个叶子节点都代表一个字符,而节点的权重通常代表字符的频率。在哈夫曼编码中,每个字符都会被赋予一个二进制编码。为了获得这些编码,我…...

Kubernetes Cluster IP,Node IP,Pod IP间通信原理解析
目录 1、Cluster IP2、Node IP3、NodePort4、Pod IP5、LoadBalancer6、三种IP间通信6.1、Pod IP 与 Pod IP 通信6.2、Pod IP 与 Cluster IP 通信6.3、Node IP 与 Pod IP 通信6.4、Node IP 与 Cluster IP 7、YAML 示例7.1、ClusterIP Service7.2、LoadBalancer Service 1、Clust…...
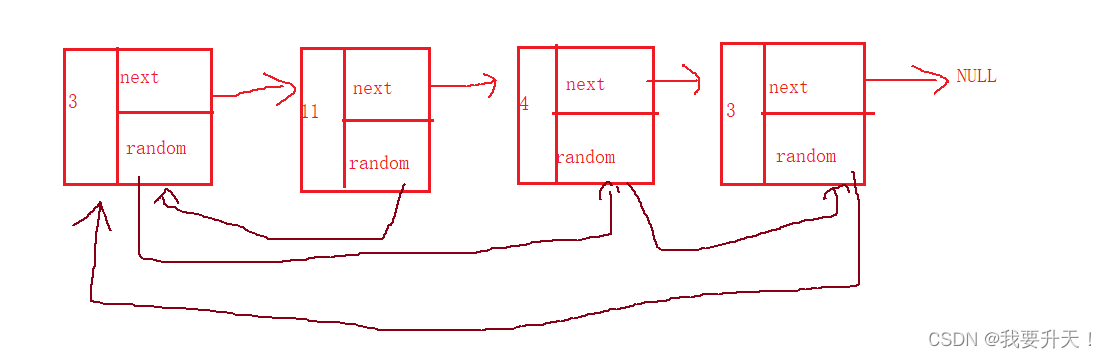
随机链表的深拷贝
1.题目 解题思路一:暴力求解,先创建新链表,然后把旧链表中的val和next指针给复制到新链表中,根据旧链表中的random指针所指向的旧链表中的val值找到所对应的节点,记录该节点的位置,就像数组一样,…...

328_C++_HTTP_HTTP协议传输data数据,为什么要进行base64编解码操作?
http传输data数据的时候,为什么必须进行base64转码后才能有效发送,接收方也必须base64转码后才能有效接受? HTTP HTTP传输数据时,使用Base64编码并不是必须的,但它确实在某些情况下非常有用。以下是为什么在某些情况…...
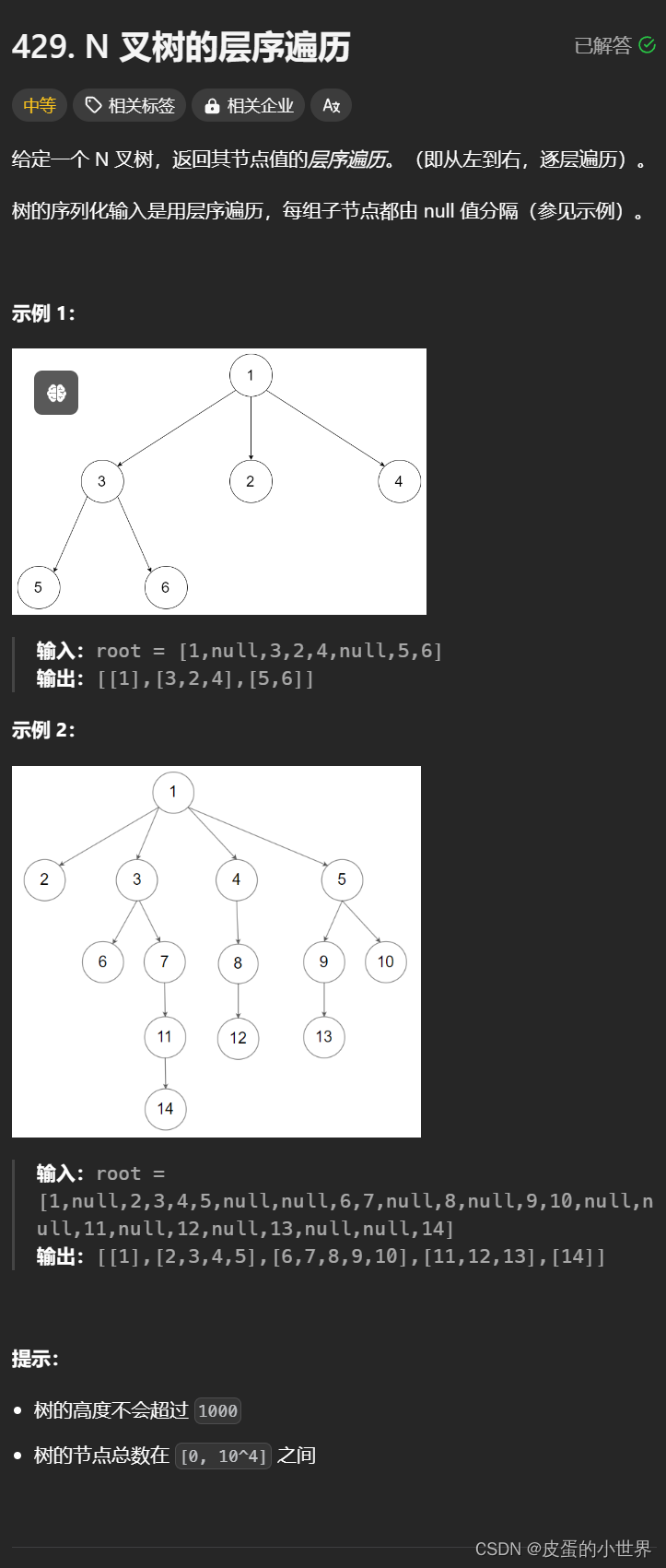
【二叉树】Leetcode N 叉树的层序遍历
题目讲解 429. N 叉树的层序遍历 算法讲解 在做层序遍历的时候由于它的每一个结点是有val vector child组成,所以在做层序遍历的时候需要考虑它每一层结点的个数,那我们就可以使用一个queue保存每一层的结点;那么我们在做第一层的时候&am…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
