Unity 单例模式
Unity中单例模式是非常常用的写法,可以基于C#语言的几种不同方法来实现。
下面我将列出几种常见的实现方式:
1. 经典的单例模式
public class SingletonExample : MonoBehaviour
{private static SingletonExample instance;public static SingletonExample Instance{get{if (instance == null){instance = FindObjectOfType<SingletonExample>();if (instance == null){GameObject obj = new GameObject("SingletonExample");instance = obj.AddComponent<SingletonExample>();DontDestroyOnLoad(obj);}}return instance;}}private void Awake(){if (instance == null){instance = this;DontDestroyOnLoad(this.gameObject);}else if (instance != this){Destroy(gameObject);}}
}
优点:
- 易于理解和实现。
- 可以在Unity的场景中直接使用,提供了与Unity生命周期事件的结合。
缺点:
- 不是完全的线程安全。在多线程环境下,可能会创建多个实例。
如果没有在场景中找到实例,它会创建一个新的GameObject,这可能会导致意外的副作用。
2. 使用静态构造函数
public class SingletonExample
{private static readonly SingletonExample instance = new SingletonExample();static SingletonExample(){}private SingletonExample(){}public static SingletonExample Instance{get{return instance;}}
}
优点:
- 实现简单,线程安全由CLR (公共语言运行时)保证。
- 静态构造函数只会被执行一次,保证了实例的唯一性。
缺点:
- 实例在程序运行时立即创建,无论是否使用,可能会导致资源的浪费。
不适合在Unity场景对象中使用,因为它与MonoBehaviour断开了联系,不能直接应用到GameObject上。
3. 使用Lazy类型确保线程安全
using System;public class SingletonExample
{private static readonly Lazy<SingletonExample> lazy =new Lazy<SingletonExample>(() => new SingletonExample());public static SingletonExample Instance { get { return lazy.Value; } }private SingletonExample(){}
}
优点:
- 实现简单,线程安全由CLR (公共语言运行时)保证。
- 静态构造函数只会被执行一次,保证了实例的唯一性。
缺点:
- 实例在程序运行时立即创建,无论是否使用,可能会导致资源的浪费。
不适合在Unity场景对象中使用,因为它与MonoBehaviour断开了联系,不能直接应用到GameObject上。
4. 双重校验锁(Double-Check Locking)
public class SingletonExample
{private static SingletonExample instance;private static readonly object lockObject = new object();public static SingletonExample Instance{get{if (instance == null){lock (lockObject){if (instance == null){instance = new SingletonExample();}}}return instance;}}private SingletonExample(){}
}
优点:
- 线程安全,并且在需要时才创建实例。
- 相对于Lazy,在早期的.NET版本中也可以使用。
缺点:
- 实现复杂,需要正确管理锁,否则可能会导致死锁。
- 性能开销,每次访问实例时都需要进行双重检查。
- 不直接与MonoBehaviour兼容,同样不适合直接应用于Unity场景中的对象。
总结:
在选择实现单例的方法时,应当考虑是否需要延迟初始化、是否在多线程环境中使用、以及是否需要与Unity的MonoBehaviour系统集成等因素。
在Unity中,经常使用第一种方法,因为它能够更好地与Unity的组件和生命周期集成。
不过,如果你在Unity项目中需要使用单例模式管理非MonoBehaviour类型的资源或类,例如数据管理或服务类,那么**第三种方法(Lazy)**是一个非常好的选择。
相关文章:

Unity 单例模式
Unity中单例模式是非常常用的写法,可以基于C#语言的几种不同方法来实现。 下面我将列出几种常见的实现方式: 1. 经典的单例模式 public class SingletonExample : MonoBehaviour {private static SingletonExample instance;public static SingletonEx…...
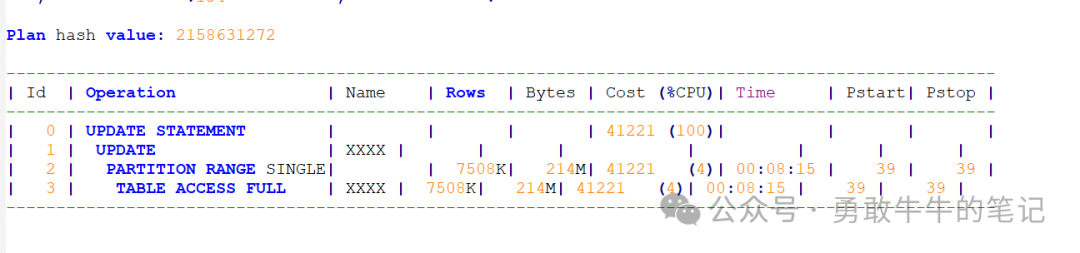
Oracle-一次TX行锁堵塞事件
问题背景: 接用户问题报障,应用服务出现大量会话堆积现象,数据库锁堵塞严重,需要协助进行问题定位和排除。 问题分析: 登录到数据库服务器上,首先查看一下数据库当前的等待事件情况,通过gv$ses…...

Gtid方式搭建主从复制+MHA高可用集群
GTID是什么 GTID(全局事务标识符),它用于唯一标识一个事务。每个GTID由三个部分组成: 服务器唯一标识符事务序列号全局事务标识符使用gtid可以简化主从复制的配置和管理,减少由于复制链路终端、主从数据不一致等问题带来的风险如何开启GTID: 在/etc/my.cnf文件中添加如下…...
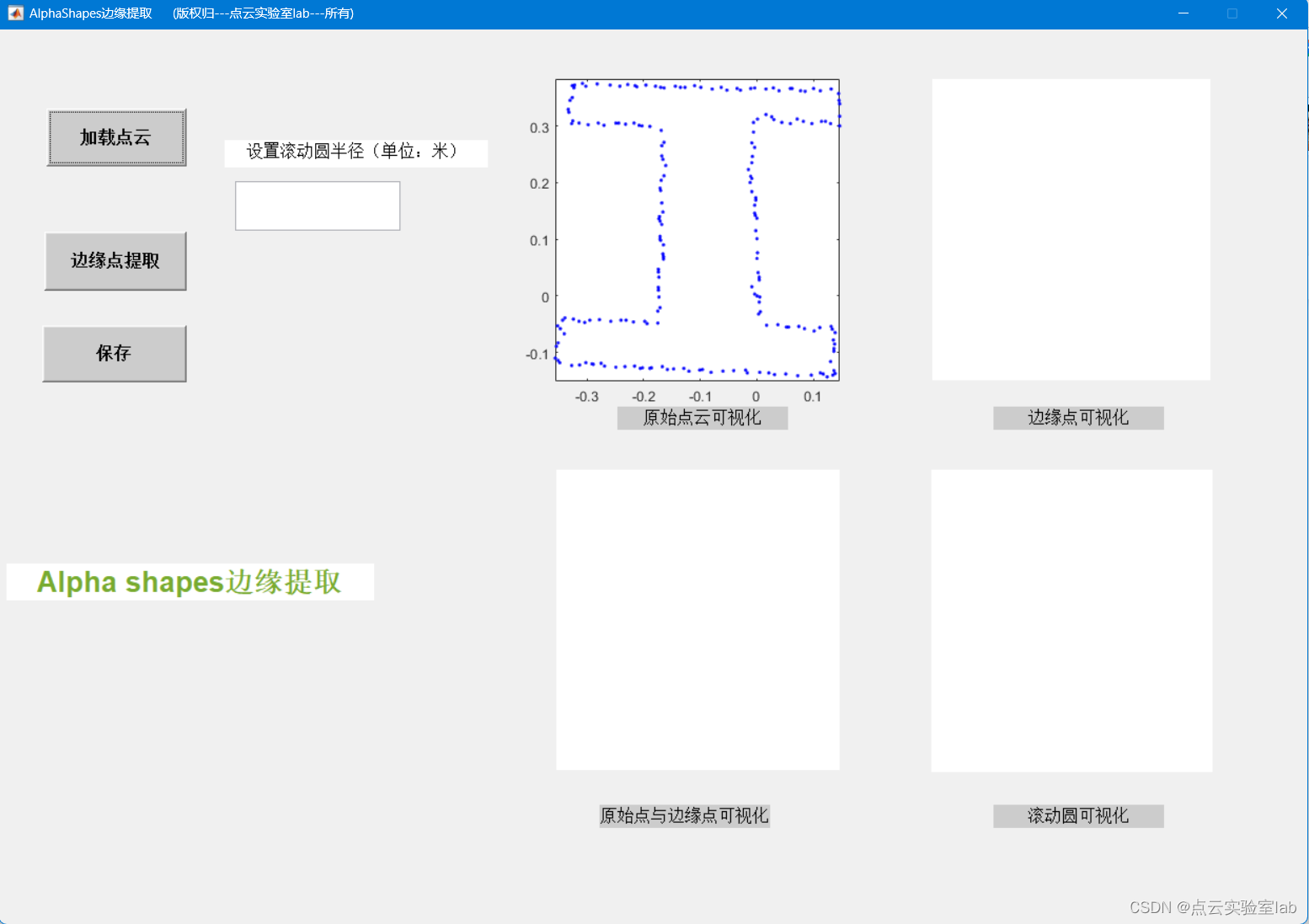
基于matlab GUI的Alpha shapes边缘提取
1、程序介绍 本程序是基于matlab语言,使用alpha shapes算法实现点云边缘提取。算法具体原理参考博客:基于alpha shapes的边缘点提取(matlab)-CSDN博客。该程序包括3个按钮:加载点云、边缘点提取、保存。其中࿰…...

[Android]常见的包管理方式
在Android开发中,包管理主要是通过构建和依赖管理工具来处理。下面列举了几种最常见和主流的包管理方式: 一、Gradle Gradle 是 Android 官方推荐的构建工具,几乎成为了 Android 开发的标准。它支持自定义构建逻辑、依赖管理、多项目构建等…...

每日10亿数据的日志分析系统OOM
背景 一个每日10亿数据的日志清洗系统,主要工作就是从消息队列中消费各种各样的日志,然后对日志进行清洗,例如:用户敏感信息(姓名、手机号、身份证)进行脱敏处理,然后把清理完的数据交付给其他系统使用。 我们项目中,…...

智能驱动,精准管理:打造高效干部管理系统
干部管理系统是现代组织管理中不可或缺的工具,它通过信息技术的应用,提高了干部管理的效率和准确性。干部管理系统的主要功能包括: 1. 信息管理:系统可以存储和管理干部的个人信息,包括基本资料、工作经历、教育背景、…...
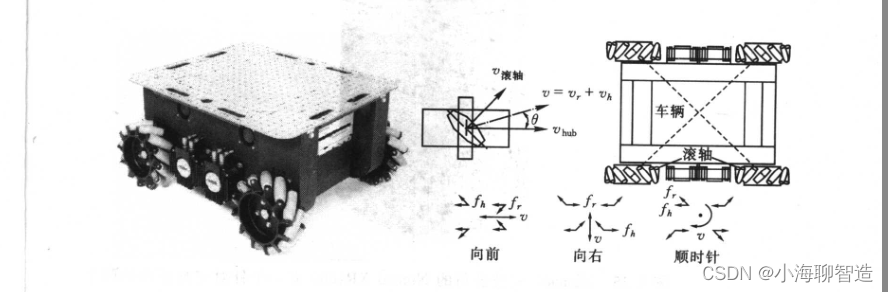
轮式机器人简介
迄今为止,轮子一般是移动机器人学和人造交通车辆中最流行的运动机构。它可达到很高的效率, 如图所示, 而且用比较简单的机械就可实现它的制作。 另外,在轮式机器人设计中,平衡通常不是一个研究问题。 因为在所有时间里,轮式机器人一般都被设计成在任何时间里所有轮子均与地接…...

已知哈夫曼节点个数,求哈夫曼字符编码数
哈夫曼编码(Huffman Coding)是一种用于无损数据压缩的嫡编码(权编码)算法。 在哈夫曼树中,每个叶子节点都代表一个字符,而节点的权重通常代表字符的频率。在哈夫曼编码中,每个字符都会被赋予一个二进制编码。为了获得这些编码,我…...

Kubernetes Cluster IP,Node IP,Pod IP间通信原理解析
目录 1、Cluster IP2、Node IP3、NodePort4、Pod IP5、LoadBalancer6、三种IP间通信6.1、Pod IP 与 Pod IP 通信6.2、Pod IP 与 Cluster IP 通信6.3、Node IP 与 Pod IP 通信6.4、Node IP 与 Cluster IP 7、YAML 示例7.1、ClusterIP Service7.2、LoadBalancer Service 1、Clust…...
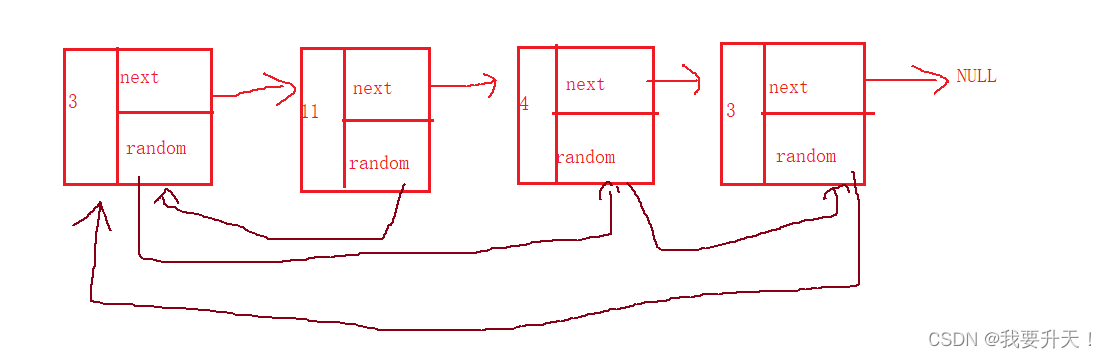
随机链表的深拷贝
1.题目 解题思路一:暴力求解,先创建新链表,然后把旧链表中的val和next指针给复制到新链表中,根据旧链表中的random指针所指向的旧链表中的val值找到所对应的节点,记录该节点的位置,就像数组一样,…...

328_C++_HTTP_HTTP协议传输data数据,为什么要进行base64编解码操作?
http传输data数据的时候,为什么必须进行base64转码后才能有效发送,接收方也必须base64转码后才能有效接受? HTTP HTTP传输数据时,使用Base64编码并不是必须的,但它确实在某些情况下非常有用。以下是为什么在某些情况…...
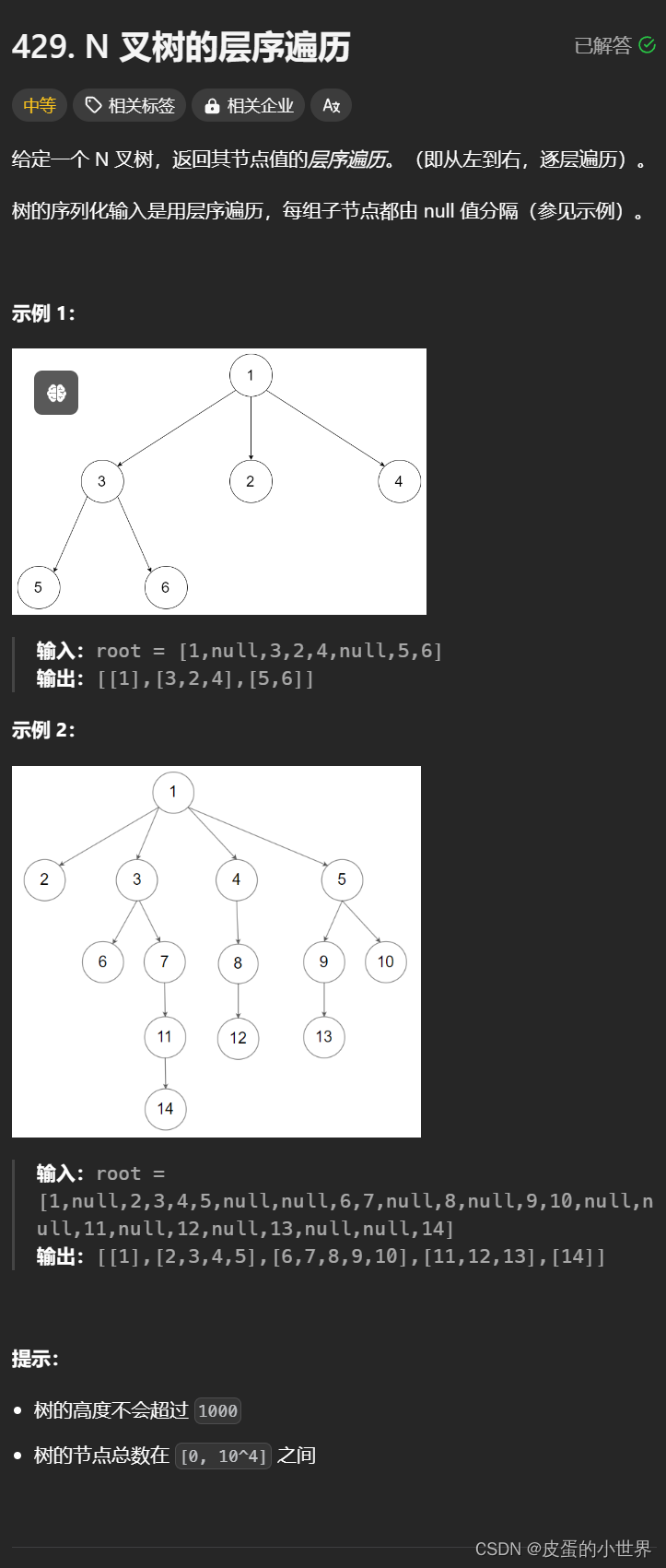
【二叉树】Leetcode N 叉树的层序遍历
题目讲解 429. N 叉树的层序遍历 算法讲解 在做层序遍历的时候由于它的每一个结点是有val vector child组成,所以在做层序遍历的时候需要考虑它每一层结点的个数,那我们就可以使用一个queue保存每一层的结点;那么我们在做第一层的时候&am…...

Spring AI
目录 一、Spring AI 1、Spring AI简介 1.1、四次工业革命发展和变革 1.2、什么是人工智能? 1.3、人工智能的发展历程 1.4、什么是大模型? 1.5、如何训练大模型? 一、Spring AI 1、Spring AI简介 Spring AI Java接入人工智能大模型 1.1、四次工业革命发展和变革 人类…...

fiori SAP ui5 动态改变控件颜色
使用CustomData动态改变控件颜色 有时候我们需要改变控件颜色,对于高度封装的控件,显然改变控件CSS是比较困难的,幸好SAP UI5预设了一个customData的属性,每个控件都能使用她。 如下代码是判断汇率是否有改变,如果改…...

RabbitMQ php amqp
Linux debian 安装 Windows php amqp 扩展 PECL :: Package :: amqp 将 php_amqp.dll 复制到 php 的 ext 目录下 将 rabbitmq.4.dll 复制到 c:\windows\system32 目录下 php.ini extensionamqp...
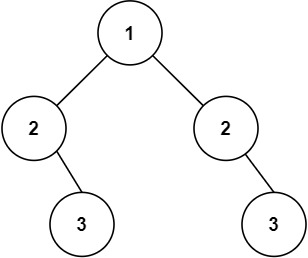
对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true示例 2: 输入:root [1,2,2,null,3,null,3] 输出:falses 思路:我刚开始是想着用…...

浅浅总结SQL中的事务.
在现实生活中有很多的线上支付的场景,当支付的时候,一方资金减少,另一方资金增加,在执行前后,两者的总体数额需要相同,为了保证这个操作的完整,所以提出了事务,那我们先来去写一个示例ÿ…...

C++ | Leetcode C++题解之第76题最小覆盖子串
题目: 题解: class Solution { public:unordered_map <char, int> ori, cnt;bool check() {for (const auto &p: ori) {if (cnt[p.first] < p.second) {return false;}}return true;}string minWindow(string s, string t) {for (const au…...

什么可以替代iframe?
网页嵌套中,iframe曾几何时不可一世,没有其他更好的选择! iframe即内联框架,作为网页设计中的一种技术,允许在一个网页内部嵌套另一个独立的HTML文档。尽管它在某些场景下提供了便利,但也存在多方面的缺陷…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
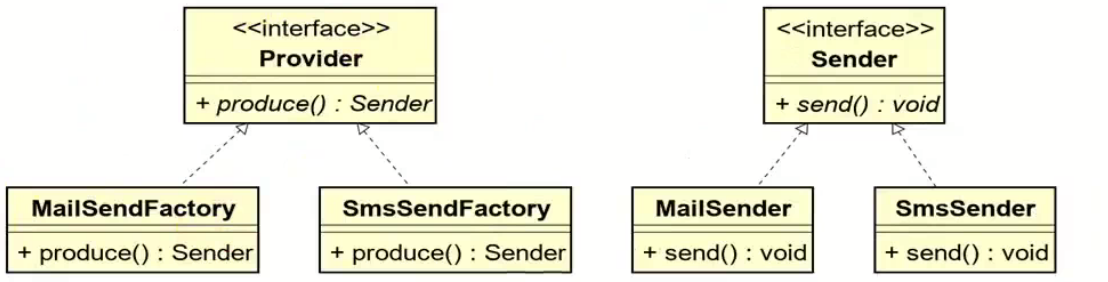
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
