【回溯算法】【Python实现】最大团问题
文章目录
- @[toc]
- 问题描述
- 回溯算法
- `Python`实现
- 时间复杂性
文章目录
- @[toc]
- 问题描述
- 回溯算法
- `Python`实现
- 时间复杂性
问题描述
-
给定无向图 G = ( V , E ) G = (V , E) G=(V,E),如果 U ⊆ V U \subseteq V U⊆V,且对任意 u u u, v ∈ U v \in U v∈U有 ( u , v ) ∈ E (u , v) \in E (u,v)∈E,则称 U U U是 G G G的完全子图
-
G G G的完全子图 U U U是 G G G的一个团当且仅当 U U U不包含在 G G G的更大的完全子图中, G G G的最大团是指 G G G中所含顶点数最多的团
-
如果 U ⊆ V U \subseteq V U⊆V且对任意 u u u, v ∈ U v \in U v∈U,有 ( u , v ) ∉ E (u , v) \notin E (u,v)∈/E,则称 U U U是 G G G的空子图
-
G G G的空子图 U U U是 G G G的独立集当且仅当 U U U不包含在 G G G的更大的空子图中, G G G的最大独立集是 G G G中所含顶点数最多的独立集
-
对于任意无向图 G = ( V , E ) G = (V , E) G=(V,E),其补图 G ˉ = ( V ′ , E ′ ) \bar{G} = (V^{'} , E^{'}) Gˉ=(V′,E′)定义为: V ′ = V V^{'} = V V′=V, E ′ = { ( u , v ) ∣ ( u , v ) ∉ E } E^{'} = \set{(u , v) \mid (u , v) \notin E} E′={(u,v)∣(u,v)∈/E}
-
如果 U U U是 G G G的完全子图,则它是 G ˉ \bar{G} Gˉ的空子图,反之亦然,因此, G G G的团与 G ˉ \bar{G} Gˉ的独立集之间存在一一对应关系,特别地, U U U是 G G G的最大团,当且仅当 U U U是 G ˉ \bar{G} Gˉ的最大独立集
-
无向图 G G G和 G G G的补图 G ˉ \bar{G} Gˉ如下图所示

回溯算法
- 图 G G G的最大团和最大独立集问题都可以看作图 G G G的顶点集 V V V的子集选取问题,因此,可用子集树表示问题的解空间,解最大团问题的回溯法与解装载问题的回溯法十分相似
- 设当前扩展结点 Z Z Z位于解空间树的第 i i i层,在进入左子树前,必须确认从顶点 i i i到已选入的顶点集中每个顶点都有边相连,在进入右子树前,必须确认还有足够多的可选择顶点,使得算法有可能在右子树中找到更大的团
Python实现
def find_maximum_clique(graph):n = len(graph)vertices = list(range(n))max_clique = []def is_clique(current_clique):# 约束函数: 判断给定的顶点集合是否构成一个团(完全子图)for i in range(len(current_clique)):for j in range(i + 1, len(current_clique)):if not graph[current_clique[i]][current_clique[j]]:return Falsereturn Truedef bound(current_clique, vertices):# 限界函数return len(current_clique) + len(vertices)def backtrack(vertices, current_clique):nonlocal max_cliqueif not vertices:if len(current_clique) > len(max_clique):max_clique.clear()max_clique.extend(current_clique)returnvertex = vertices.pop(0)current_clique.append(vertex)neighbors = []for v in vertices:if graph[vertex][v]:neighbors.append(v)# 选择当前顶点并加入团if is_clique(current_clique):backtrack(neighbors, current_clique)# 恢复回溯前状态current_clique.pop()# 不选择当前顶点if bound(current_clique, vertices) > len(max_clique):backtrack(vertices, current_clique)backtrack(vertices, [])return max_cliquegraph = [[0, 1, 0, 1, 1],[1, 0, 1, 0, 1],[0, 1, 0, 0, 1],[1, 0, 0, 0, 1],[1, 1, 1, 1, 0]
]maximum_clique = find_maximum_clique(graph)print(f'最大团: {maximum_clique}')
最大团: [0, 1, 4]
时间复杂性
- 解最大团问题的回溯算法所需的计算时间为 O ( n 2 n ) O(n 2^{n}) O(n2n)
相关文章:

【回溯算法】【Python实现】最大团问题
文章目录 [toc]问题描述回溯算法Python实现时间复杂性 问题描述 给定无向图 G ( V , E ) G (V , E) G(V,E),如果 U ⊆ V U \subseteq V U⊆V,且对任意 u u u, v ∈ U v \in U v∈U有 ( u , v ) ∈ E (u , v) \in E (u,v)∈E,则称…...

CMakeLists.txt语法规则:foreach 循环基本用法
一. 简介 cmake 中除了 if 条件判断之外,还支持循环语句,包括 foreach()循环、while()循环。 本文学习 CMakeLists.txt语法中的循环语句。 CMakeLists.txt语法中 有两种 循环实现方式:foreach循环与 while循环。 二. CMakeLists.txt语法规则…...
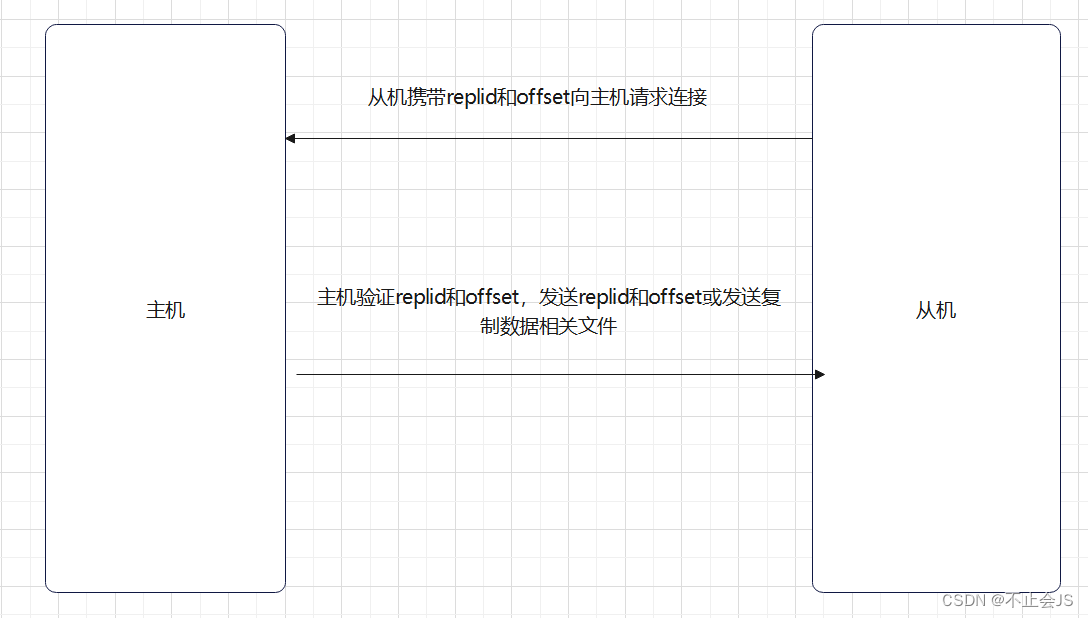
redis集群-主从机连接过程
首先从机需要发送自身携带的replid和offset向主机请求连接 replid:replid是所有主机在启动时会生成的一个固定标识,它表示当前复制流的id,当从机第一次请求连接时,主机会将自己的replid发送给从机,从机在接下来的请求…...

去哪里找高清视频素材?推荐几个短视频素材免费网站
在数字时代,视频内容的质量直接影响观众的吸引力和留存率。尤其是高清、4K视频素材和可商用素材,它们在提升视觉质量和叙事深度方面起到了至关重要的作用。以下是一些国内外的顶级视频素材网站,它们提供的资源将为您的创作提供极大的支持和灵…...

从互联网医院源码到搭建:开发视频问诊小程序的技术解析
如今,视频问诊小程序作为医疗服务的一种新形式,正逐渐受到人们的关注和青睐。今天,小编将为您详解视频问诊小程序的开发流程。 一、背景介绍 互联网医院源码是视频问诊小程序开发的基础,它提供了一套完整的医疗服务系统框架&…...
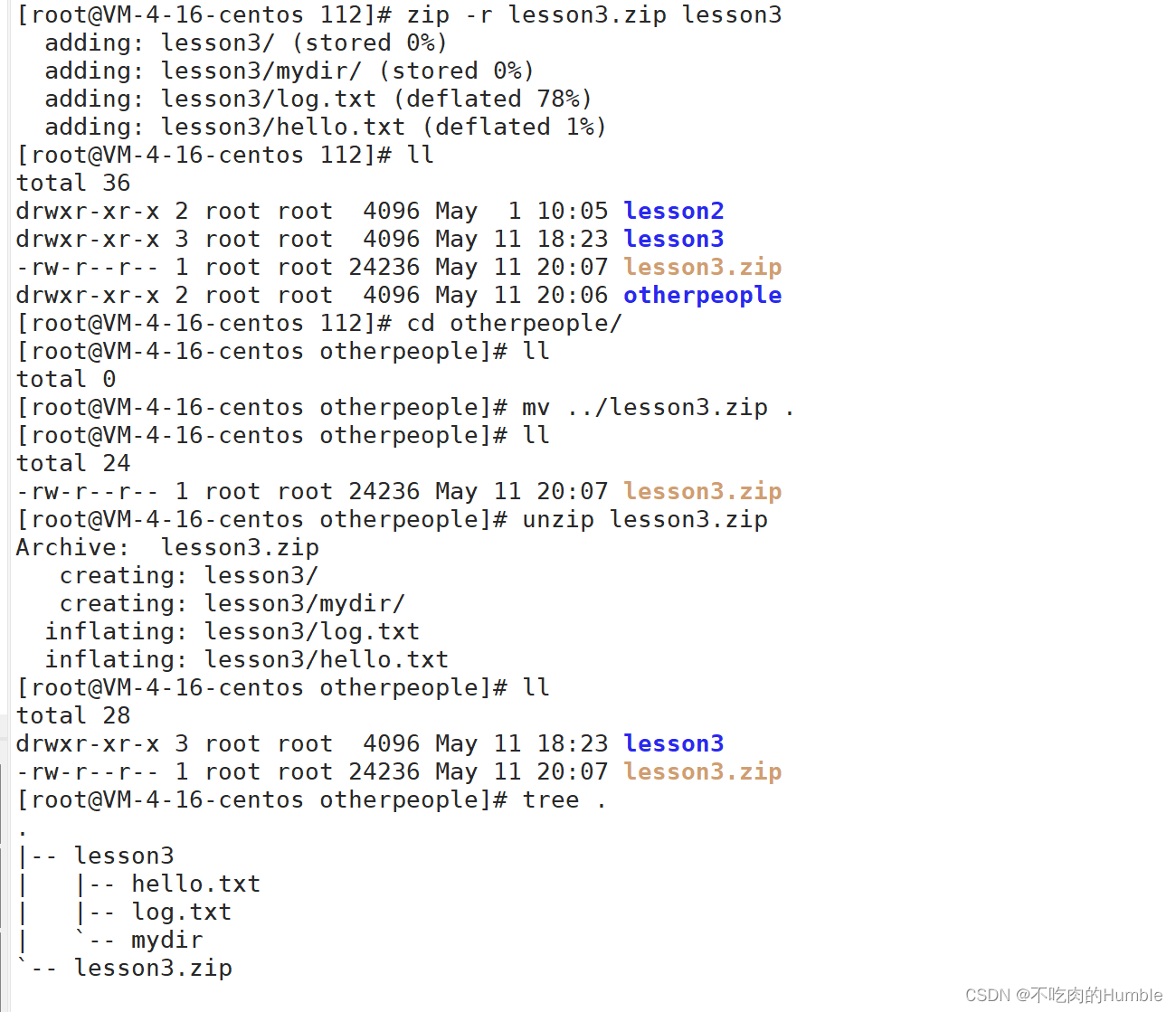
【Linux】常见指令(二)
mv指令 mv命令是move的缩写,可以用来移动文件或者将文件改名(move (rename) files) 是Linux系统下常用的命令,经常用来备份文件或者目录 功能: 1.剪切文件或者目录 2.对文件或者目录进行重命名 常用选项: -f …...

python元类与C#、Java中的反射
Python的元类和C#中的反射 在概念上有一定的相似性,但它们的目的和使用方式有所不同。 Python的元类: 元类(Metaclass)是控制类创建的类。它们定义了类的创建过程,可以修改类的行为。元类通过定制类的创建过程&…...
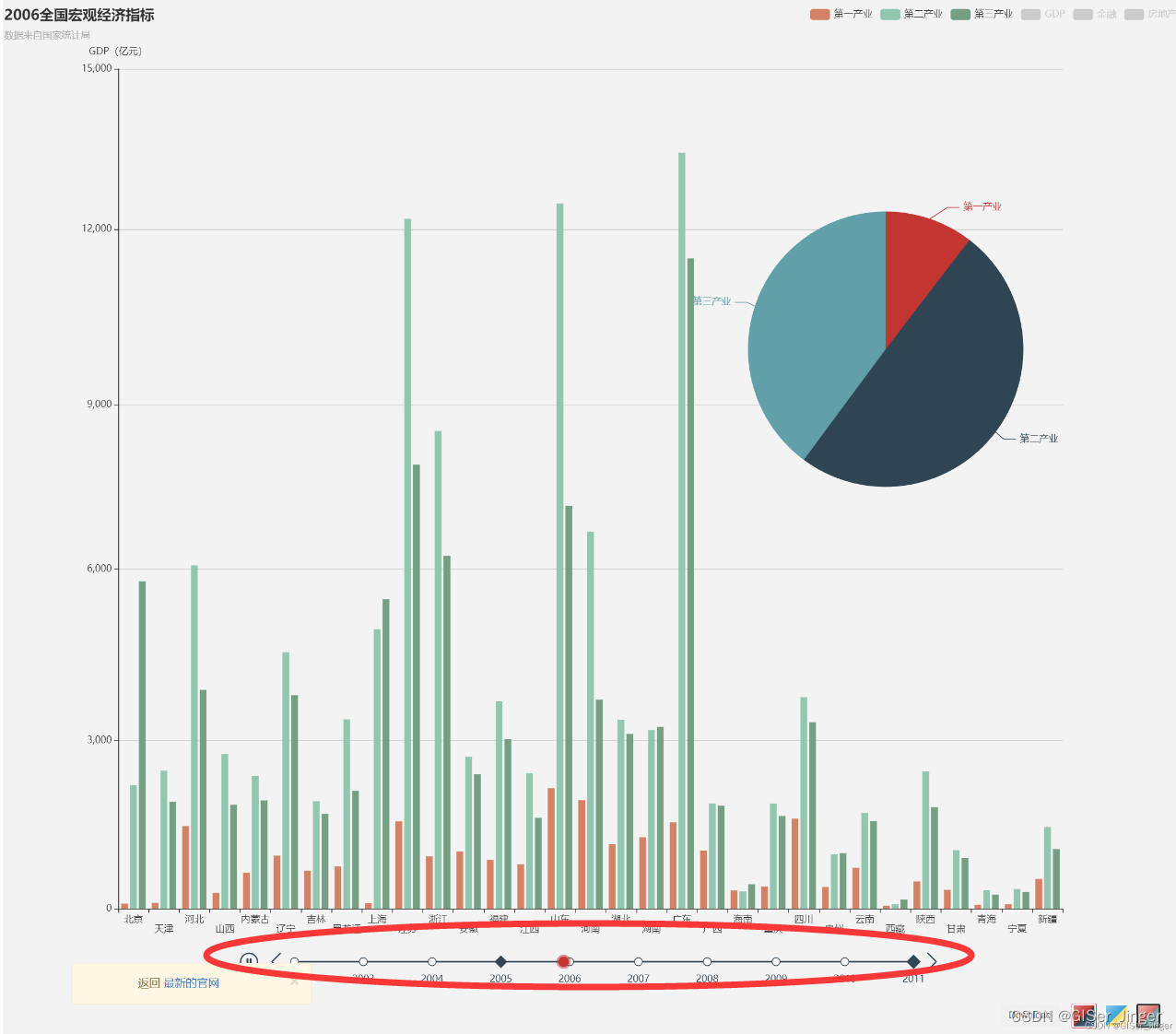
Echart.js绘制时间线并绑定事件
<template><div id"app"><!-- 定义一个具有指定宽高的容器,用于渲染图表 --><div ref"timeline" style"width: 800px; height: 600px;"></div></div> </template><script> import *…...

Flutter弹窗链-顺序弹出对话框
效果 前言 弹窗的顺序执行在App中是一个比较常见的应用场景。比如进入App首页,一系列的弹窗就会弹出。如果不做处理就会导致弹窗堆积的全部弹出,严重影响用户体验。 如果多个弹窗中又有判断逻辑,根据点击后需要弹出另一个弹窗,这…...
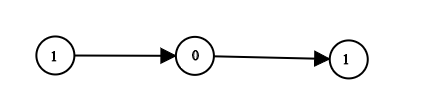
1290.二进制链表转整数
给你一个单链表的引用结点 head。链表中每个结点的值不是 0 就是 1。已知此链表是一个整数数字的二进制表示形式。 请你返回该链表所表示数字的 十进制值 。 示例 1: 输入:head [1,0,1] 输出:5 解释:二进制数 (101) 转化为十进制…...

P8803 [蓝桥杯 2022 国 B] 费用报销
P8803 [蓝桥杯 2022 国 B] 费用报销 分析 最值问题——DP 题意分析:从N张票据中选,且总价值不超过M的票据的最大价值(背包问题) K天限制 一、处理K天限制: 1.对于输入的是月 日的格式,很常用的方式是…...
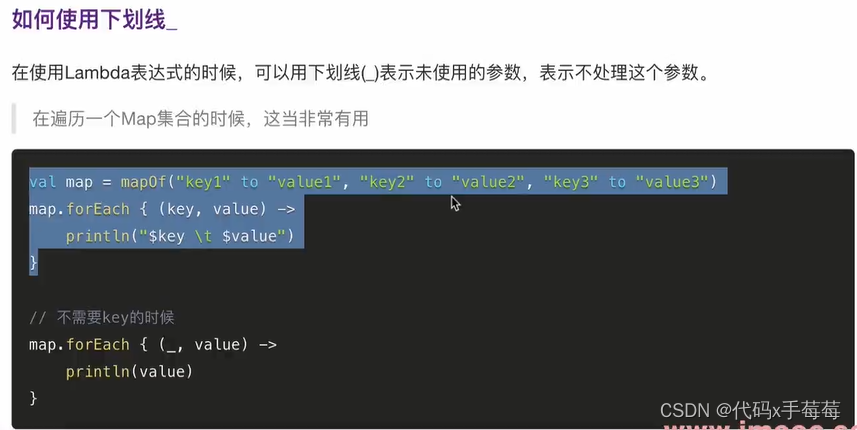
【Android】Kotlin学习之Lambda表达式
java和kotlin对比 Lambda语法 Lambda隐形参数 it 也可以不使用指定的名称it, 可以 自定义 Lambda 使用下划线...
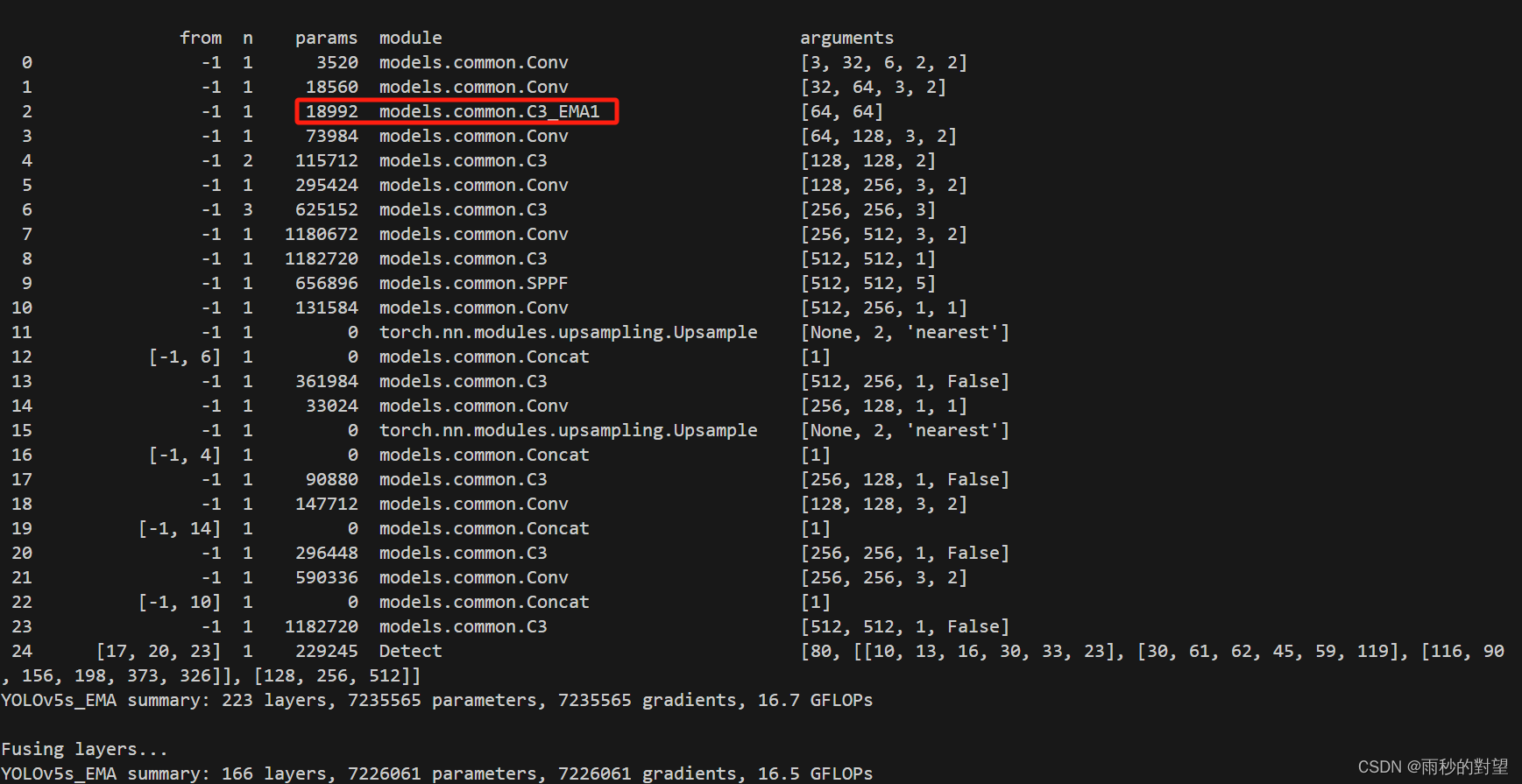
YOLOv5-7.0改进(四)添加EMA注意力机制
前言 关于网络中注意力机制的改进有很多种,本篇内容从EMA注意力机制开始! 往期回顾 YOLOv5-7.0改进(一)MobileNetv3替换主干网络 YOLOv5-7.0改进(二)BiFPN替换Neck网络 YOLOv5-7.0改进(三&…...
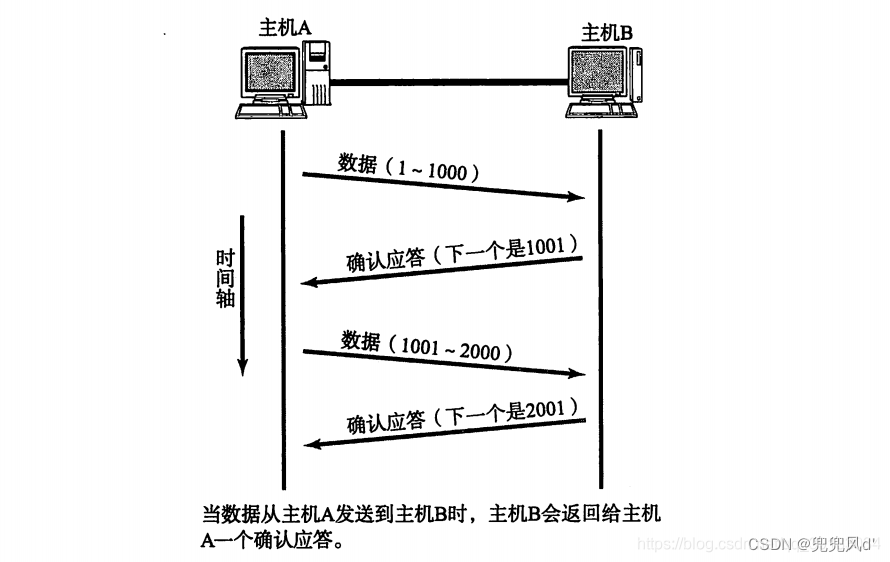
TCP协议的确认应答机制
TCP(Transmission Control Protocol)是一种面向连接的、可靠的、基于字节流的传输层协议,它在网络通信中扮演着至关重要的角色。其中,确认应答机制是TCP协议中的一个核心概念,它确保了数据的可靠传输。本文将详细介绍J…...
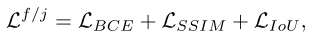
【论文阅读笔记】MAS-SAM: Segment Any Marine Animal with Aggregated Features
1.论文介绍 MAS-SAM: Segment Any Marine Animal with Aggregated Features MAS-SAM:利用聚合特征分割任何海洋动物 Paper Code(空的) 2.摘要 最近,分割任何模型(SAM)在生成高质量的对象掩模和实现零拍摄图像分割方面表现出卓越…...

C语言中的精确宽度类型
概述 在 C 语言标准库 <stdint.h> 中定义了一系列精确宽度的整数类型,这些类型保证了它们的位数宽度,从而允许编写跨平台的可移植代码。以下是一些常用的精确宽度整数类型: int8_t: 8位有符号整数uint8_t: 8位无符号整数int16_t: 16位…...

大数据比赛-环境搭建(一)
1、安装VMware Workstation 链接:https://pan.baidu.com/s/1IvSFzpnQFl3svWyCGRtEmg 提取码:ukpo 内有安装包及破解方式,安装教程。 2、下载Ubuntu系统 阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区 (aliyun.com) 点击下载ÿ…...
微信小程序原生组件使用
1、video组件使用 <view class"live-video"><video id"myVideo" src"{{videoSrc}}" bindplay"onPlay" bindfullscreenchange"fullScreenChange" controls object- fit"contain"> </video&g…...

[数据集][目标检测]纸箱子检测数据集VOC+YOLO格式8375张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):8375 标注数量(xml文件个数):8375 标注数量(txt文件个数):8375 标注…...
2024HW Linux应急响应基础学习
首先展示关于Linux的关键目录,这是应急响应查看的关键: 常用命令 top //查看进程资源的占用情况 ps -aux //查看进程 直接写ps aux也可以 netstat -antpl //查看网络连接 ls -alh /proc/pid //查看某个pid对应的可执行程序 pid记得修改 lsof /…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
