波动性悖论:为何低风险股票长期跑赢高风险对手?
从去年开始,“红利低波”类的产品净值稳步向上,不断新高,让很多人关注到了A股“分红高”、“波动率低”这两类股票。分红高的公司更受投资者青睐,这从基本面的角度很容易理解,那么波动率低的股票明明波动更小,那为什么涨的更好呢?
1、低波异象
首先,我们从一个违反错觉的现象说起:“低波异象”。传统金融理论,如资本资产定价模型(CAPM),主张投资的预期回报率与其贝塔系数(β)或市场相关风险成正比例关系。根据这一理论,承担较高系统性风险的资产应当获得较高的预期收益,而风险较低的资产则预期收益相对较低。但是,与CAPM模型的预测相反,众多学术研究的实证分析发现,在较长的时间范围内,低波动性(即低风险)股票相较于高波动性(即高风险)股票实际上展现出了更优的收益表现和更小的价格波动,这一现象被称为“低波动率异象”。
金融学领域的两位学者贝克和豪根研究了 21个发达市场和 12个新兴市场在 1990 年至2011年间低波动股票和高波动股票的表现,他们发现低波动异象是全球股市广泛存在的长期定价异常在所研究的 33 个国家或地区均存在低波动异象。此外,他们的研究还显示发达市场的低波动异象较新兴市场更强,且在他们的测试样本中,相较其他市场,A股市场的低波动异象程度很低。
在A股市场,低波动率的股票相对于高波动率的股票在大部分时间里都能跑赢,特别是在2017年之后,低波/高波的相对收益率稳定向上,至今一直长期有效。
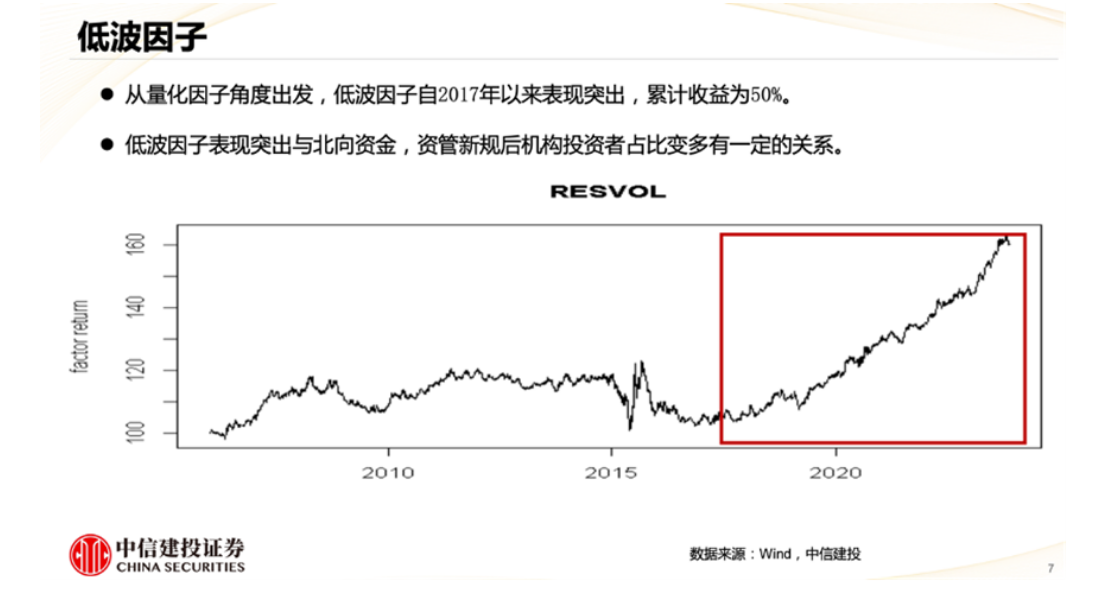
数据来源:Wind,中信建投,少数派投资
2、低波异象的原因
低波异象的构成可以从以下几个方面来理解:
1)投资者倾向于对高波动性股票过度乐观,导致这些股票被高估,而低波动性股票则可能被市场忽视,从而被低估。一些行为金融学理论认为,投资者可能因为彩票偏好、代表性偏差、过度自信等非理性行为,对高波动性股票有过度需求,而对低波动性股票需求不足。
2.)从风险补偿的角度来看,投资者可能认为低波动性股票的风险较小,因此要求的回报率较低,这可能导致这些股票的市场价格低于其真实价值。
3)在量化投资领域,低波动性因子被用作一种投资策略,通过选择波动率较低的股票来构建投资组合,以期获得稳定的收益。在欧美市场,低波动率因子的SmartBeta产品也受到投资者的广泛追捧,助推了低波动率因子的收益率。
4)相比多头操作,空头的限制较多,导致投资者对这类股票的多空交易存在不对称性,促使高波动股票的高估。该效应在做空机制不够完善的A股市场可能更加明显。
3、高波动率vs低波动率
低波异象的存在挑战了传统的金融理论,并且为投资者提供了一种可能获得超额收益的策略。然而,这种策略并非没有风险,低波动率的股票在牛市来临时往往会跑输大盘。那么作为低波动率的反面 -- 高波动率股票,他们在配置时的特色是什么?
投资高波动率股票也有其特定的优势和考虑因素,主要包括:
1)市场情绪:在市场情绪积极时,投资者可能更愿意承担风险,这时高波动率股票可能会受到追捧,从而推高其价格。在市场反弹期间,高波动率股票往往能够迅速恢复并可能提供快速的回报。
2)潜力更大:在某些市场周期或行业轮动中,高波动率股票可能会受益,因为投资者可能会寻求更高的风险以期获得更高的回报。高波动率股票可能更受动量交易者的青睐。高波动率股票可能在短期内提供较高的收益潜力。如果投资者能够准确预测市场走势,高波动性股票可能会带来较大的盈利空间。
3)基本面发生更大更长期的变革:高波动率股票往往属于市场领导者或快速增长的公司,这些公司可能在创新、市场占有率增长或行业变革中处于前沿。即使是短期波动或者回撤,但是从中长期来看,目前的价值仍然很便宜。
然而,高波动率股票的风险也相对较高,因此投资者在追求高收益的同时,需要对相关风险有充分的认识和准备。此外,投资高波动率股票可能需要更频繁的监控和更高的交易成本。在构建投资组合时,投资者最好还是配置更多的低波动率股票,同时,根据基本面与情绪面的变化,配置一定的高波动股票,万一“牛市”这次真的来了呢?
相关文章:

波动性悖论:为何低风险股票长期跑赢高风险对手?
从去年开始,“红利低波”类的产品净值稳步向上,不断新高,让很多人关注到了A股“分红高”、“波动率低”这两类股票。分红高的公司更受投资者青睐,这从基本面的角度很容易理解,那么波动率低的股票明明波动更小ÿ…...
版)
环信设置头像昵称(安卓android)版
在此真的要吐槽吐槽环信,那么大的公司,文档那么乱。。。真的像一坨屎一样,翻个demo东翻西翻,官网论坛看的眼瞎。。。几乎要放弃了,还好百度到别人的看了看弄出来了 1、首先,要确认自己用的是哪个环信的UI库…...

Rust:用 Warp 库实现 Restful API 的简单示例
直接上代码: 1、源文件 Cargo.toml [package] name "xcalc" version "0.1.0" edition "2021"# See more keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html[dependencies] warp "…...
【SpringBoot】 什么是springboot(一)?如何搭建springboot项目?
文章目录 SpringBoot第一章1、什么是springboot1、回顾ssm项目搭建流程2、springboot项目的优点2、搭建springboot项目方式1:方式2:第二章1、基本配置1、热部署2、注解3、端口配置application.properties特点application.yml特点注意4、环境配置springboot中的配置文件要求5、…...
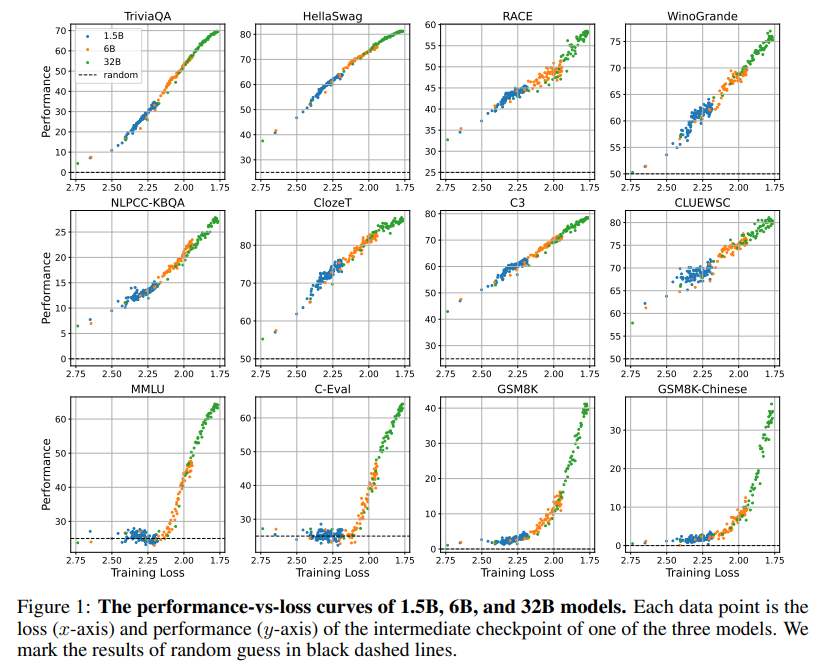
从loss角度理解LLM涌现能力
如今的很多研究都表明小模型也能出现涌现能力,本文的作者团队通过大量实验发现模型的涌现能力与模型大小、训练计算量无关,只与预训练loss相关。 作者团队惊奇地发现,不管任何下游任务,不管模型大小,模型出现涌现能力…...

debian apt 更改阿里源
1. 备份文件 cp /etc/apt/sources.list /etc/apt/sources.list.bak 2. 更改 sources.list文件内容为: deb http://mirrors.aliyun.com/debian/ buster main non-free contrib deb-src http://mirrors.aliyun.com/debian/ buster main non-free contrib deb htt…...

Spring Cloud | “微服务“ 架构 与 Spring Cloud
“微服务” 架构 与 Spring Cloud 目录: "微服务" 架构 与 Spring Cloud1. 认识架构"单体" 架构"SOA" 架构"微服务" 架构 2. "微服务架构" 的功能 :① 微服务架构的 "自动化部署"② 服务 "集中化管理"③…...

win10禁止自动更新的终极方法
添加注册表值 1.运行,输入regedit 2.打开注册表编辑器依次进入以下路径“计算机\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\WindowsUpdate\UX\Settings”。 3.在Settings项中,新建DWORD(32位)值(D),重命名为以下命名“Fl…...

笨方法自学python(二)-注释
注释和#号 程序里的注释是很重要的。它们可以用自然语言告诉你某段代码的功能是什么。在你想要临时移除一段代码时,你还可以用注解的方式将这段代码临时禁用。 # A comment, this is so you can read your program later. # Anything after the # is ignored by py…...
wireshark的安装使用及相关UDP、TCP、 ARP
初步了解: 进入wireshark后如图: 从图中可以看到很多网络连接在操作的时候我们需要监测哪些 我们可以直接在本地的运行框中输入ipconfig来查看 如图: 从以上图片中我们可以清楚地看到哪些网络连接已经连接的我们只需要按需监测他们即可 但…...

【软考】模拟考卷错题本2024-05-11
1 设计模式- 适配器模式 基本上上述的图解已经涵盖了绝大多数主流的设计模式和其特点。理解记忆下即可,这里对下午的考题也有帮助的。 2 计算机组成原理 cpu 访问速度 这个真的是憨憨咯~看到内存就选内存,题目都没审好。这里的速度比cpu内部的要比外部的…...

VMware虚拟机提示内存不足
VMware虚拟机,k8s集群搭建内存不足的问题 疑问:我的电脑是8G8G双通道的内存,当我在搭建k8s集群时给master-2G内存,node1-3G内存,node2-3G内存; 当依次打开虚拟机到node2时VM提示“物理内存不足,…...

视频批量剪辑指南:一键合并视频并添加背景音乐,高效便捷
在数字化时代,视频剪辑已经成为了一项常见且重要的技能。无论是制作家庭影片、工作展示还是社交媒体内容,掌握高效的视频剪辑技巧都能极大地提升我们的工作效率和创作质量。本文将为您介绍云炫AI智剪中高效的视频批量剪辑方法,让您能够一键合…...

讲讲C++四种类型转换
在C中,类型转换(或称为类型转换运算符)是用来将一个数据类型转换为另一个数据类型的机制。C提供了四种类型转换:静态类型转换(Static Cast)、动态类型转换(Dynamic Cast)、重新解释类…...

探索LLM在广告领域的应用——大语言模型的新商业模式和新个性化广告的潜力
概述 在网络搜索引擎的领域中,广告不仅仅是一个补充元素,而是构成了数字体验的核心部分。随着互联网经济的蓬勃发展,广告市场的规模已经达到了数万亿美元,并且还在持续扩张。广告的经济价值不断上升,它已经成为支撑大…...

MBR与GPT分区表
文章目录 MBR分区表MBR分区表结构MBR分区表项查看U盘的分区表信息查看系统中所有磁盘的分区类型获取分区表信息 GPT分区表保护性MBRGPT分区表头格式GPT分区表项格式分区类型分区属性分区表项内容 MBR分区表 CHS :磁头(Heads)、柱面(Cylinder…...
OGG几何内核开发-BRepAlgoAPI_Fuse与BRep_Builder.MakeCompound比较
最近在与同事讨论BRepAlgoAPI_Fuse与BRep_Builder.MakeCompound有什么区别。 一、从直觉上来说,BRepAlgoAPI_Fuse会对两个实体相交处理,相交的部分会重新的生成相关的曲面。而BRep_Builder.MakeCompound仅仅是把两个实体组合成一个新的实体,…...

C语言 | Leetcode C语言题解之第67题二进制求和
题目: 题解: void reserve(char* s) {int len strlen(s);for (int i 0; i < len / 2; i) {char t s[i];s[i] s[len - i - 1], s[len - i - 1] t;} }char* addBinary(char* a, char* b) {reserve(a);reserve(b);int len_a strlen(a), len_b st…...
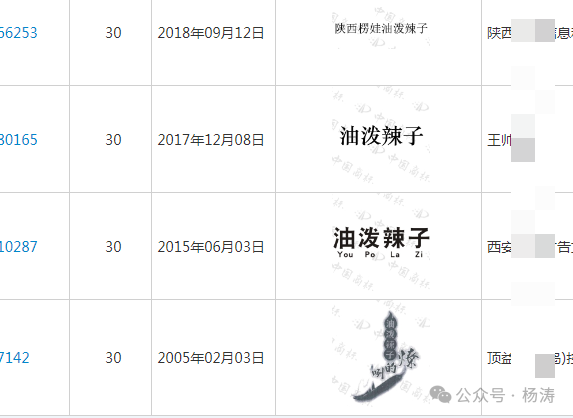
油泼辣子在食品类别可以申请成商标不!
前阵韩国人在美国申请“chili crunch”油泼辣子作为商标,还准备禁止华人餐馆使用投诉侵权并索赔,普推知产老杨在USPTO上面检索发现,这个人申请的主要是30类方便食品的调味品,商标分类是全球通用的。 商标名称不能申请本类所属的通…...

深入探索MySQL视图
前言 在数据库的世界里,MySQL视图作为数据抽象的一把利剑,为我们提供了一种灵活而高效的方式来管理和查询数据。它不仅能够简化复杂的查询逻辑,还能在不改动底层数据结构的前提下,实现数据的定制化展示与访问控制。本文旨在深入解…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
