深入探索MySQL视图
前言
在数据库的世界里,MySQL视图作为数据抽象的一把利剑,为我们提供了一种灵活而高效的方式来管理和查询数据。它不仅能够简化复杂的查询逻辑,还能在不改动底层数据结构的前提下,实现数据的定制化展示与访问控制。本文旨在深入解析MySQL视图的核心概念、高级特性以及在实际开发中的高效运用策略,帮助开发者解锁视图的全部潜能。
一、MySQL视图基础
1.1 视图的定义
视图是一个虚拟表,其内容由查询定义,不包含实际存储的数据。它就像是一个窗口,透过这个窗口,我们可以按照特定的方式查看基础表中的数据,而不直接操作底层数据。
1.2 创建与使用视图
创建视图的基本语法为:
CREATE VIEW view_name AS SELECT column1, column2,... FROM table_name WHERE condition;
使用视图如同操作普通表一样简单,通过SELECT、UPDATE(如果允许的话)、DELETE等语句即可。
二、高级特性与优化策略
2.1 更新视图的条件与限制
并非所有视图都支持更新操作。理解何时及如何使视图成为可更新的是关键。通过WITH CHECK OPTION确保视图更新时的数据一致性。
2.2 视图算法的选择
了解MERGE与TEMPTABLE算法的差异,根据查询需求选择最合适的算法类型,以优化性能。
2.3 性能考量
深入分析视图对数据库性能的影响,包括如何通过合理设计减少不必要的计算和I/O操作。
三、视图的维护与高级应用场景
3.1 维护视图
掌握如何修改、删除及重命名视图,保持数据库架构的灵活性和适应性。
3.2 数据迁移与兼容性
视图作为数据库迁移的桥梁,如何利用它来平滑过渡,确保业务连续性。
3.3 定制化数据展示与安全策略
通过视图实现数据的分层次展示,同时结合权限管理,强化数据安全防护。
四、实战案例分析
分享几个典型场景下,视图如何被巧妙地应用于解决实际问题,包括数据过滤、报表生成、权限控制等。
结语
MySQL视图是数据库设计与开发中的重要工具,它不仅简化了数据操作,还为数据的安全性和灵活性提供了更多可能性。通过深入理解其原理与高级用法,开发者能够更高效地构建和维护数据库应用,满足日益复杂多变的业务需求。掌握视图的艺术,让数据管理变得更加直观和高效。
相关文章:

深入探索MySQL视图
前言 在数据库的世界里,MySQL视图作为数据抽象的一把利剑,为我们提供了一种灵活而高效的方式来管理和查询数据。它不仅能够简化复杂的查询逻辑,还能在不改动底层数据结构的前提下,实现数据的定制化展示与访问控制。本文旨在深入解…...
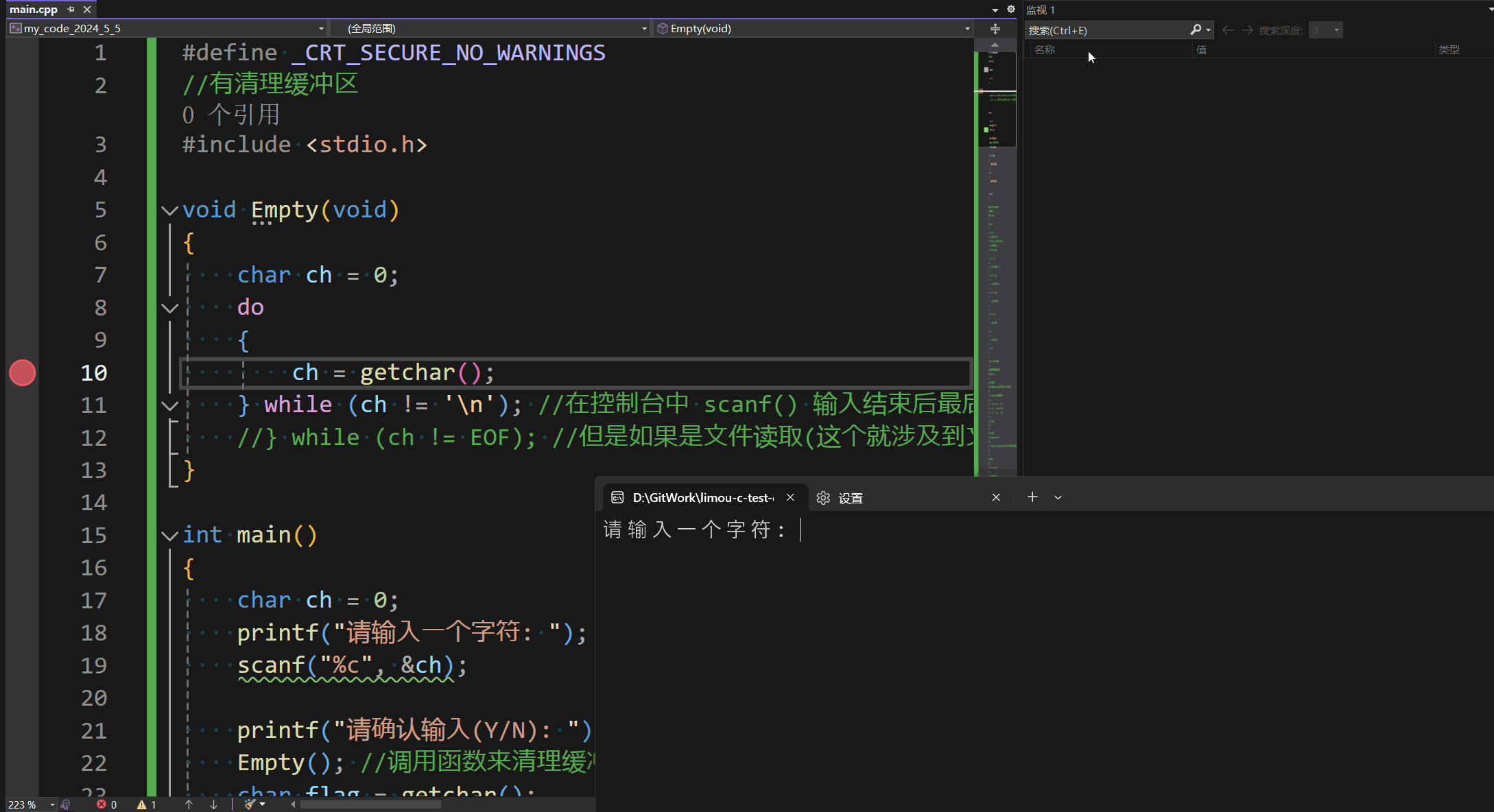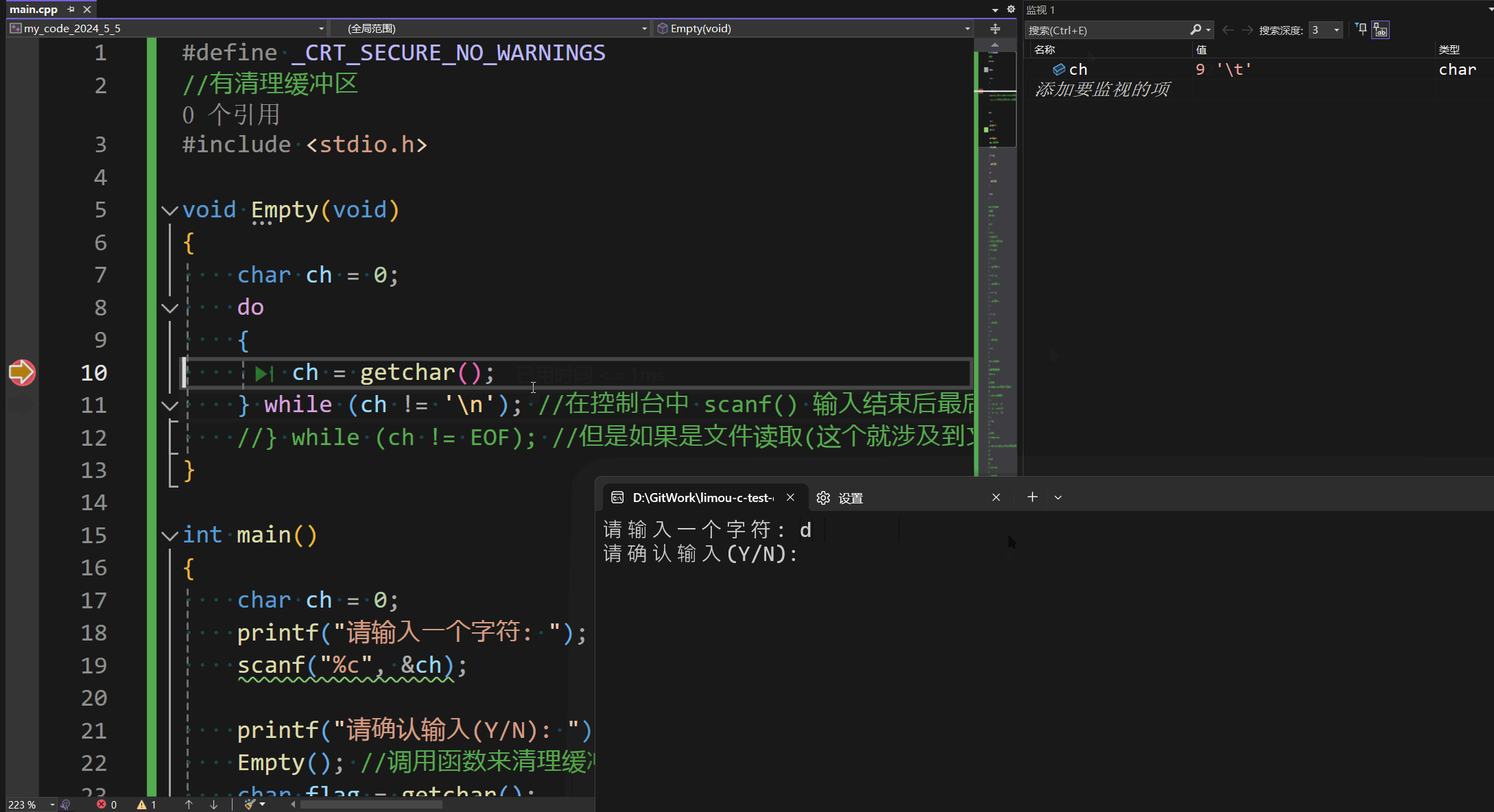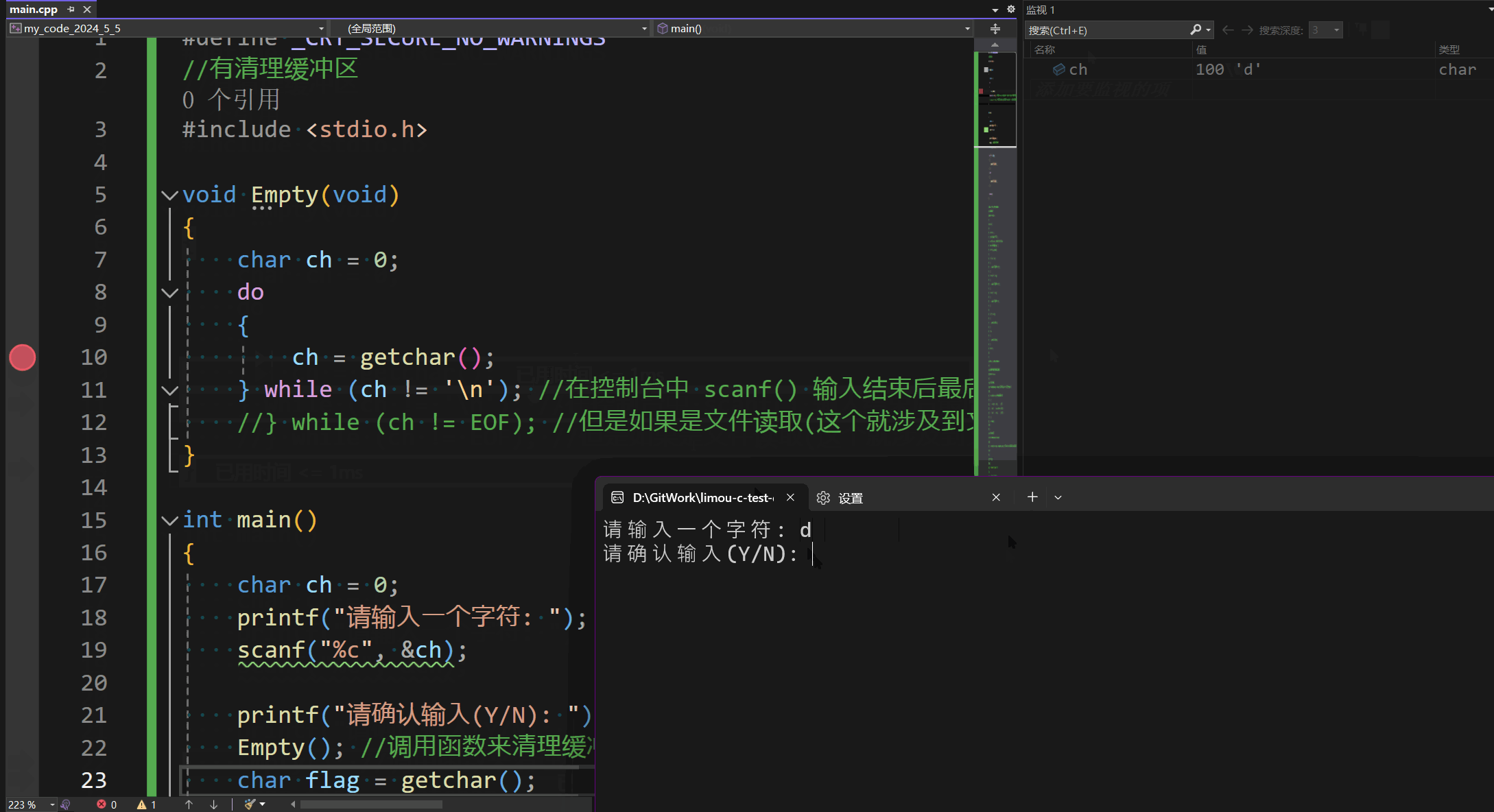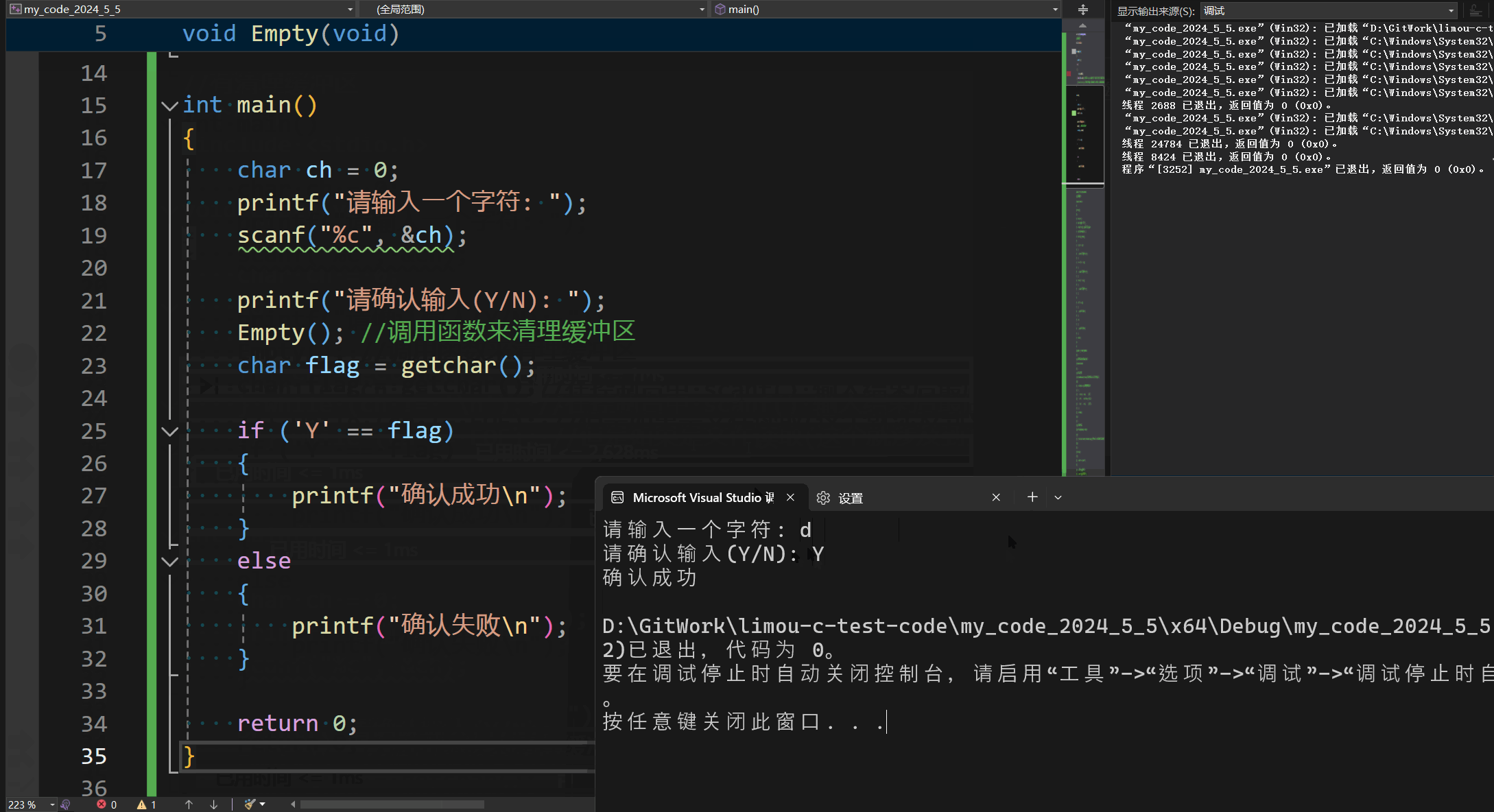
C语言逻辑语句
叠甲:以下文章主要是依靠我的实际编码学习中总结出来的经验之谈,求逻辑自洽,不能百分百保证正确,有错误、未定义、不合适的内容请尽情指出! 文章目录 1.何为控制语句2.控制语句-分支语句2.1.if2.2.switch 3.控制语句-循…...
C++青少年简明教程:基础知识
C青少年简明教程:基础知识 电脑程序设计(Computer programming),或称程序设计(programming),是给出解决特定问题程序的过程,程序设计往往以某种程序设计语言为工具,给出这…...
[AutoSar]lauterbach_001_ORTI_CPUload_Trace
目录 关键词平台说明一、ORTI概述二、ORTI文件的生成三、ORTI文件的导入四、Trace 功能4.1 Trace 功能菜单介绍4.2 Trace功能的配置4.3 Trace MCDS 设置4.4 Task Switches断点的设置4.5 Trace 数据的录取4.6 CPU 负载和Task调度的查看 关键词 嵌入式、C语言、autosar、OS、BSW…...

课程设计 大学生竞赛系统
课程设计 大学生竞赛系统 wx:help-assignment 学生用户: wx:help-assignment 首页:推荐一些竞赛,热门活动等; 广场:用户可以通过广场来发表动态,同时也可以查看别人发布的动态,并且可以 关注…...

优先队列全面讲解
主题: 优先队列是一种非常有用的数据结构,它让你能够管理一组数据,使得每次访问或移除数据时,总是得到当前集合中优先级最高(或最低)的那个元素。这个特性让优先队列非常适用于需要快速访问集合中最重要元…...

即插即用篇 | YOLOv8 引入多光谱通道注意力 | 频率领域中的通道注意力网络
本改进已集成到 YOLOv8-Magic 框架。 注意力机制,尤其是通道注意力,在计算机视觉领域取得了巨大成功。许多工作聚焦于如何设计高效的通道注意力机制,同时忽略了一个基本问题,即通道注意力机制使用标量来表示通道,这很困难,因为会造成大量信息的丢失。在这项工作中,我们从…...

Topaz Video AI 5.0.3激活版 AI视频无损缩放增强
Topaz Video AI专注于很好地完成一些视频增强任务:去隔行,放大和运动插值。我们花了五年时间制作足够强大的人工智能模型,以便在真实世界的镜头上获得自然的结果。 Topaz Video AI 还将充分利用您的现代工作站,因为我们直接与硬件…...

ppt通过修改幻灯片母版修改页脚
修改幻灯片母版 幻灯片母版就可以了,就可以修改页脚...

【数组算法】598. 区间加法
给你一个 m x n 的矩阵 M 和一个操作数组 op 。矩阵初始化时所有的单元格都为 0 。ops[i] [ai, bi] 意味着当所有的 0 < x < ai 和 0 < y < bi 时, M[x][y] 应该加 1。 在 执行完所有操作后 ,计算并返回 矩阵中最大整数的个数 。 示例 1: …...
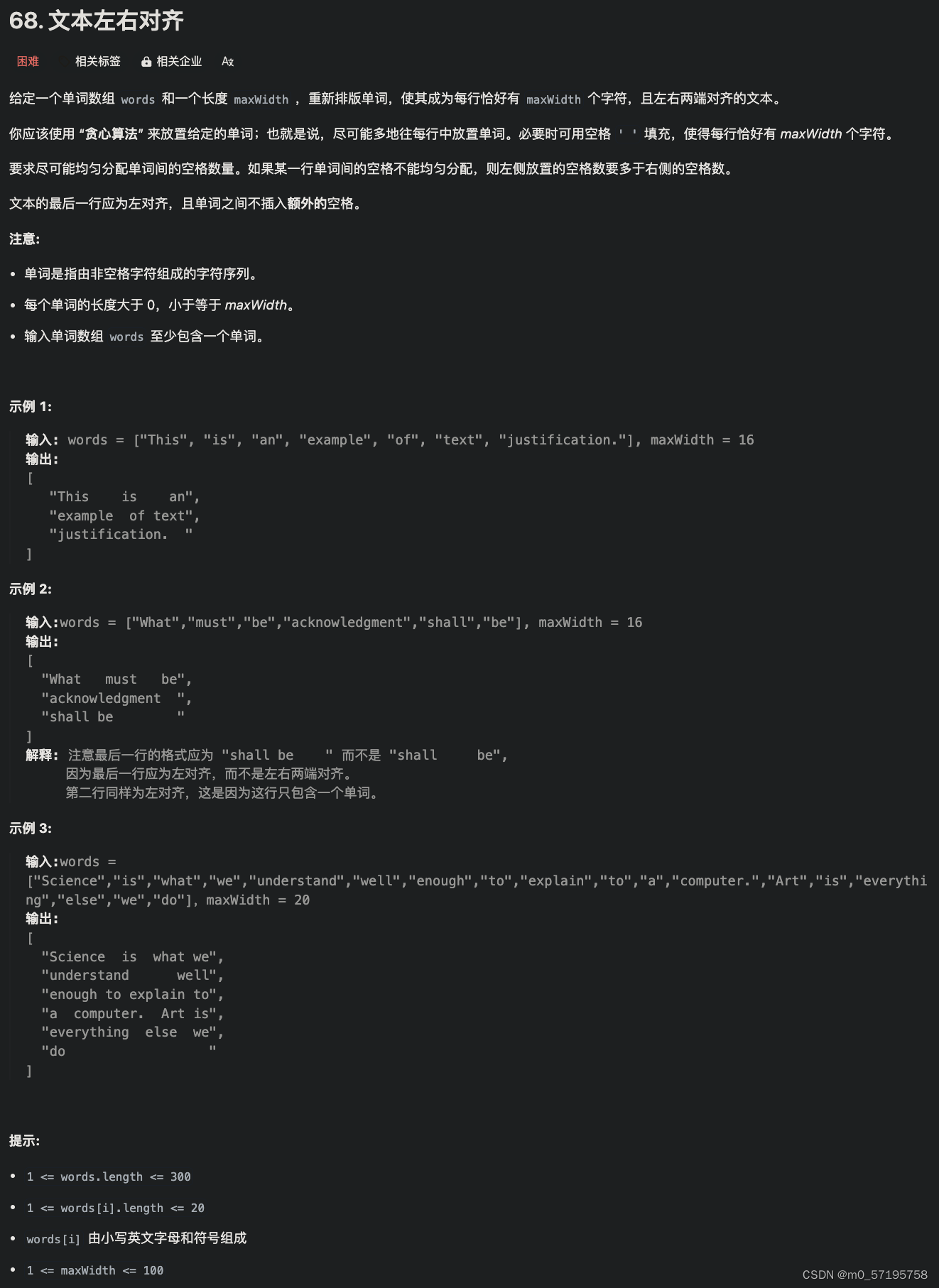
Java | Leetcode Java题解之第68题文本左右对齐
题目: 题解: class Solution {private String line(List<String> list,int maxWidth,int totalLength,boolean isLast){StringBuilder sb new StringBuilder();sb.append(list.get(0));if(list.size() 1){String ap " ".repeat(maxW…...

Windows安装MySQL 8.4.0免安装版
下载地址:MySQL :: Begin Your Download 1 管理员权限打开cmd,切换到MySQL安装路径的bin目录下 cmd> C: cmd> cd ..\mysql-8.4.0-winx64\bin 2 移除已安装的MySQL服务(若有) 2.1 停止老的MySQL服务 net stop mysql …...
初识java--javaSE(3)--方法,递归,数组,
文章目录 一 方法的使用1.1 什么是方法?main方法注意事项 1.2 方法的调用嵌套调用在方法调用时形参与实参的关系: 1.3 方法的重载方法重载的意义?总结方法重载:方法签名: 二 递归什么是递归?递归的精髓&…...

AWS ECS Fargate: 如何获取正在运行的服务
AWS Fargate 是一个无服务器计算引擎,用于容器,可以与 Amazon Elastic Container Service (ECS) 配合使用,实现容器的自动部署、管理、扩展和调整。在日常的开发和运维过程中,了解哪些服务正在运行及其状态是非常重要的。本文将介绍如何使用 Python 和 AWS SDK(boto3)来检…...

Rust 常用 Web 开源代码库
Rust的web开发有许多优秀的开源库可供选择,以下是一些值得关注的库: Web框架: Axum:由Rust社区的异步事实标准Tokio团队开发,以高性能和强大的异步支持著称。其特点包括使用无宏API将请求路由到处理程序、使用提取器以…...

零代码平台助力中国石化江苏油田实现高效评价体系
概述: 中国石化集团江苏石油勘探局有限公司面临着评价体系依赖人工处理数据、计算繁琐且容易出错的挑战。为解决这一问题,他们决定借助零代码平台明道云开发江苏油田高质量发展经济指标评价系统。该系统旨在实现原始数据批量导入与在线管理、权重及评分…...
[优选算法]------滑动窗⼝——209. 长度最小的子数组
目录 1.题目 1.解法⼀(暴⼒求解)(会超时): 2.解法⼆(滑动窗⼝): 1.算法思路: 2.手撕图解 3.代码实现 1.C 2.C语言 1.题目 209. 长度最小的子数组 给定一个含有 n…...

简述a标签target属性的取值和作用
在HTML中,<a>标签(锚标签)的target属性用于指定链接的打开方式。该属性定义了当用户点击链接时,链接将如何被打开。以下是target属性的常见取值及其作用: 1. _self(默认值) - 打开链接…...
uniapp管理后台编写,基于uniadmin和vue3实现uniapp小程序的管理后台
一,创建uniAdmin项目 打开开发者工具Hbuilder,然后点击左上角的文件,点新建,点项目。如下图。 选择uniadmin,编写项目名,然后使用vue3 记得选用阿里云服务器,因为最便宜 点击创建,等待项目创…...
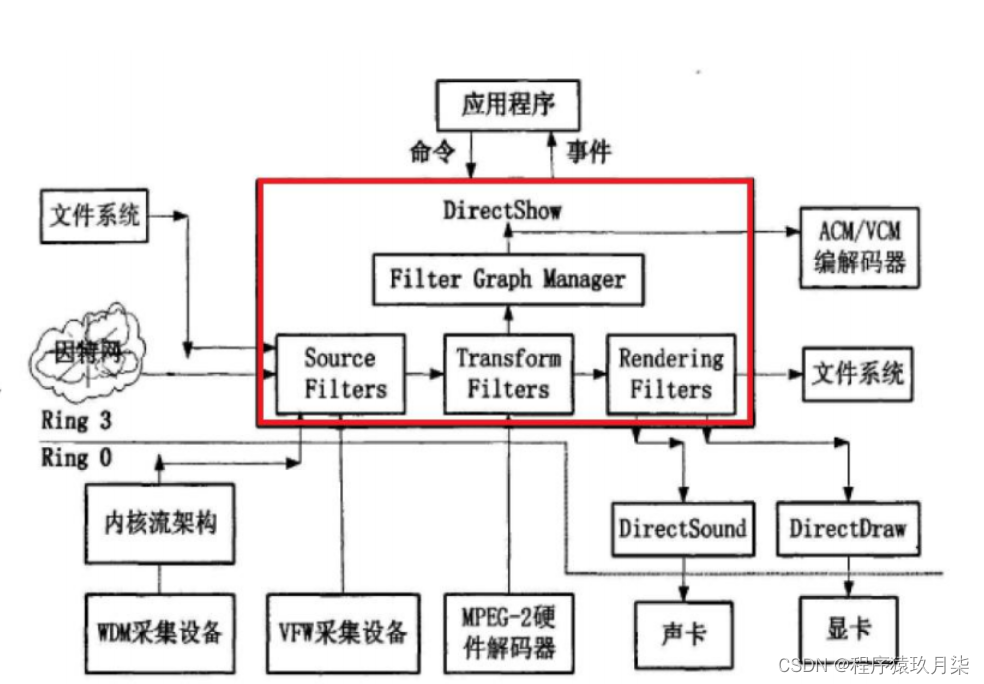
FFmpeg常用API与示例(四)——过滤器实战
1.filter 在多媒体处理中,filter 的意思是被编码到输出文件之前用来修改输入文件内容的一个软件工具。如:视频翻转,旋转,缩放等。 语法:[input_link_label1]… filter_nameparameters [output_link_label1]… 1、视…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...

2025年全国I卷数学压轴题解答
第19题第3问: b b b 使得存在 t t t, 对于任意的 x x x, 5 cos x − cos ( 5 x t ) < b 5\cos x-\cos(5xt)<b 5cosx−cos(5xt)<b, 求 b b b 的最小值. 解: b b b 的最小值 b m i n min t max x g ( x , t ) b_{min}\min_{t} \max_{x} g(x,t) bmi…...

Java严格模式withResolverStyle解析日期错误及解决方案
在Java中使用DateTimeFormatter并启用严格模式(ResolverStyle.STRICT)时,解析日期字符串"2025-06-01"报错的根本原因是:模式字符串中的年份格式yyyy被解释为YearOfEra(纪元年份),而非…...

链结构与工作量证明7️⃣:用 Go 实现比特币的核心机制
链结构与工作量证明:用 Go 实现比特币的核心机制 如果你用 Go 写过区块、算过哈希,也大致理解了非对称加密、数据序列化这些“硬核知识”,那么恭喜你,现在我们终于可以把这些拼成一条完整的“区块链”。 不过别急,这一节我们重点搞懂两件事: 区块之间是怎么连接成“链”…...
