冯喜运:5.12黄金回撤继续上涨,下周原油走势分析
【黄金消息面分析】:本周,黄金市场迎来了自4月中旬以来的最佳单周表现。周五(3月9日),金价攀升至2360.54美元/盎司,涨幅0.62%,而纽约商品交易所6月交割的黄金期货价格上涨1.5%,收报2375美元/盎司。本周累计上涨2.9%,这主要得益于美国就业数据的疲软,强化了市场对美联储降息的预期。

【黄金技术面分析】:技术上,上周一直承压短期均线一路震荡慢下行,维持弱势修正;而今日出现一波探底持续拉升,当前有所冲破了10均线2340-2345的压制,不过得等收线后,才能明确;若收盘打回去了,仍处于10均线下方,那么还是维持弱势修正,明日得继续看跌下行;反之,收盘站上10均线之上较远了,那么短期就要改变思路,去逢低看涨反弹,去测试中轨,以及通道反压点。上方关注2380-90一线阻力,下方关注2330-2340一线支撑
【原油消息面分析】:本周五(5月10日),原油市场经历了显著的价格波动。WTI 6月原油期货价格下跌1美元/桶,收报78.26美元/桶,而布伦特原油期货价格也下跌1.09美元/桶,收报82.79美元/桶。这一价格变动主要受到美国央行官员关于利率将持续保持较高水平的言论影响,引发了市场对全球最大原油消费国需求可能受阻的担忧。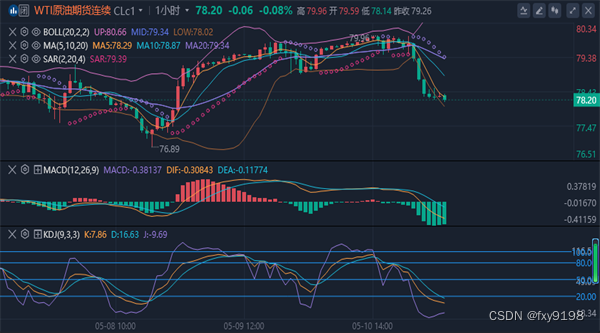
【原油技术面分析】原油期货日线来看,上周持续一周下跌收阴,周一没有延续其跌势,而是反弹收阳,周二再创下77.55美元/桶的新低后反弹,收了一根带下影线的K线,目前原油有望走一波反弹修正。四小时线来看,周五在创下77.55美元的新低后一度反弹至79上方后回落,目前运行在中轨下方,目前KDJ三线粘合,MACD的DIF和DEA金叉后向上发散运行,预计日内还将继续走反弹。虽然原油跌破了80关口的强支撑,但是周二在77.55美元有企稳的迹象,短线来看有可能会继续向上走反弹,毕竟上周跌幅比较大,技术面上也有调整的需求。综合来看,原油下周操作思路上建议以反弹做空为主,回踩低多为辅,上方短期关注79.3-79.8一线阻力,下方短期关注77.0-76.5一线支撑。
相关文章:

冯喜运:5.12黄金回撤继续上涨,下周原油走势分析
【黄金消息面分析】:本周,黄金市场迎来了自4月中旬以来的最佳单周表现。周五(3月9日),金价攀升至2360.54美元/盎司,涨幅0.62%,而纽约商品交易所6月交割的黄金期货价格上涨1.5%,收报2…...
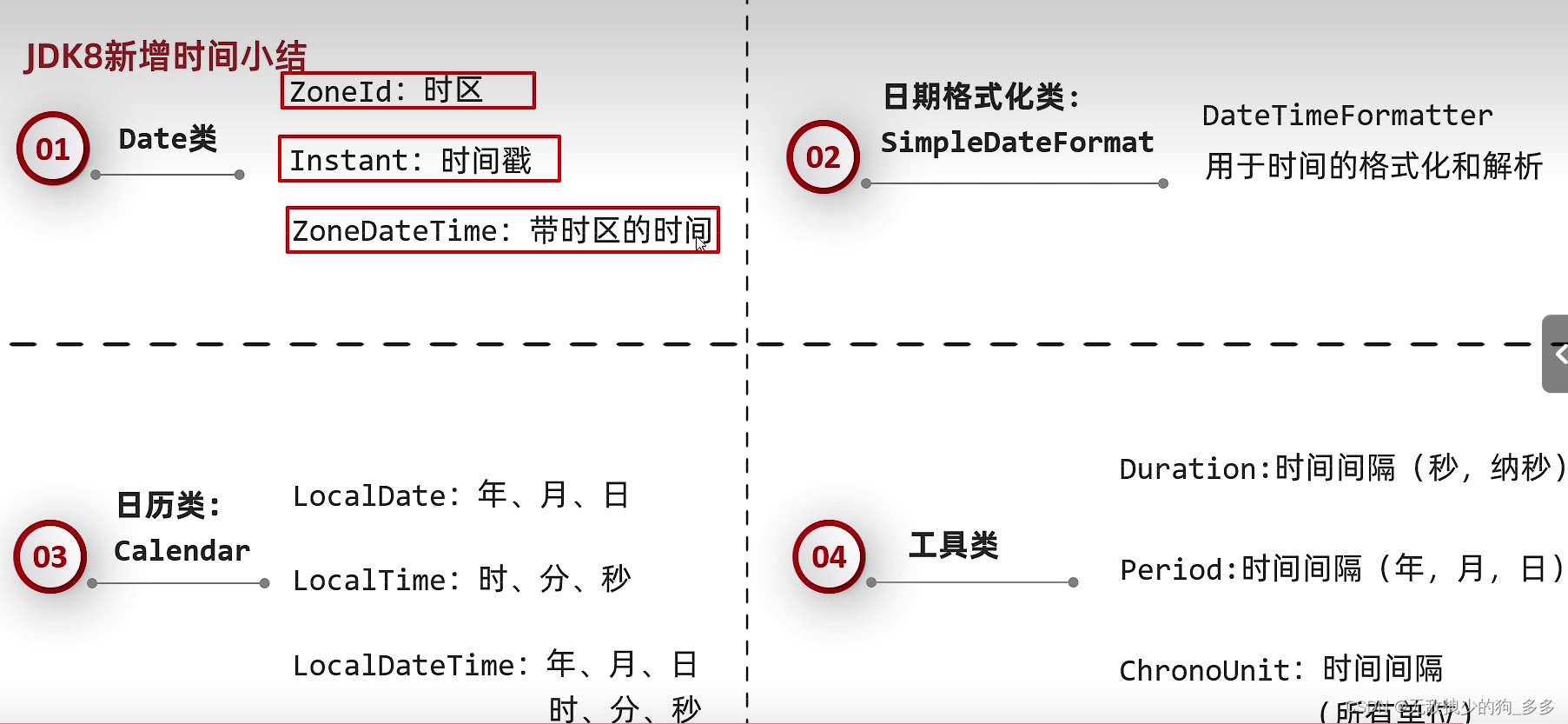
JavaEE企业级开发中常用的JDK7和JDK8的时间类
JDK7时间类 全世界的时间有一个统一的计算标准 在同一条经线上的时间是一样的 格林威治时间 简称GMT 计算核心 地球自转一天是24小时 太阳直射正好是12小时 但是误差太大 现在用原子钟来代替 用铯原子震动的频率来计算时间,作为世界的标准时间UTC 中国标准时间…...

leetcode 2316.统计无向图中无法互相到达点对数
思路:并查集 其实就是连通块的一个变形题目,一般的连通块题目要我们求的是连通个数,或者能不能到达,这里反过来问了。 首先,我们用dfs也是可以做到的,在dfs中统计每一个连通块的个数,然后用乘…...

WPS二次开发系列:如何使用WPS返回的FileUri
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 目录 什么是FileUri 在SDK中的使用场景 打开文档时…...

python删除一个文件夹所有文件
在Python中,可以使用os模块来删除一个文件夹中的所有文件,但保留文件夹本身。以下是一个简单的例子: import osdef delete_files_in_folder(folder_path):for filename in os.listdir(folder_path):file_path os.path.join(folder_path, fi…...

overflow:hidden对解决外边距塌陷的个人理解
外边距塌陷: 子元素的上外边距大于父元素的上外边距,导致边距折叠,取两者之间最大值,即子元素外边距,导致父元素上外边距失效。 解决办法:在父元素样式添加overflow:hidden;或者border:1px solid black;(不…...

【linux软件基础知识】- 文件的概念:Linux 中的文件
Linux 中的文件 在 Linux 中,文件是存储在存储设备(例如硬盘驱动器或固态驱动器)上的数据项的集合。 文件被组织为字节序列,并由文件系统中的唯一名称来标识。 以下是 Linux 中文件的一些关键特征: 字节序列:Linux 中的文件被视为字节序列。 每个字节可以表示一个字符…...
Context capture/Pix4Dmapper/AutoCAD/CASS/EPS软件的安装流程与使用方法;土方量计算;无人机摄影测量数据处理
目录 专题一 无人机摄影测量技术应用现状及其发展 专题二 基本原理和关键技术讲解 专题三 无人机影像外业数据获取 专题四 数据处理环境建立与软件熟悉 专题五 GNSS数据土方量计算 专题六 基于无人机影像数据的正射影像制作 专题七 基于无人机影像数据的三维模型制作 专…...

算法系列之堆排序实践哪家强
1.概念 堆排序是一种树形选择排序,是对简单选择排序的有效改进和优化。 堆(heap),这里所说的堆是数据结构中的堆(对应于算法),而不是内存模型中的堆(数据存储形式,还比如:栈&#…...

01-win10安装Qt5
Qt5安装教程 下载Qt5官网下载(下载很慢)镜像网站下载(有些版本没有资源)迅雷下载(推荐)百度网盘下载(推荐)安装Qt5下载Qt5 官网下载(下载很慢) 【注意】:官网下载非常慢,没有镜像下载时常20+ Qt 官网有一个专门的资源下载网站,所有的开发环境和相关工具都可以从这…...

mybatis使用及配置相关,仅做个人记录
在spring-boot项目中mybatis的配置文件在yml文件中,并没有mybatisconfig.xml文件 yml文件中配置:(来源:https://blog.51cto.com/u_16213723/8747999) mybatis:# XML文件路径,可配置多个,逗号分…...
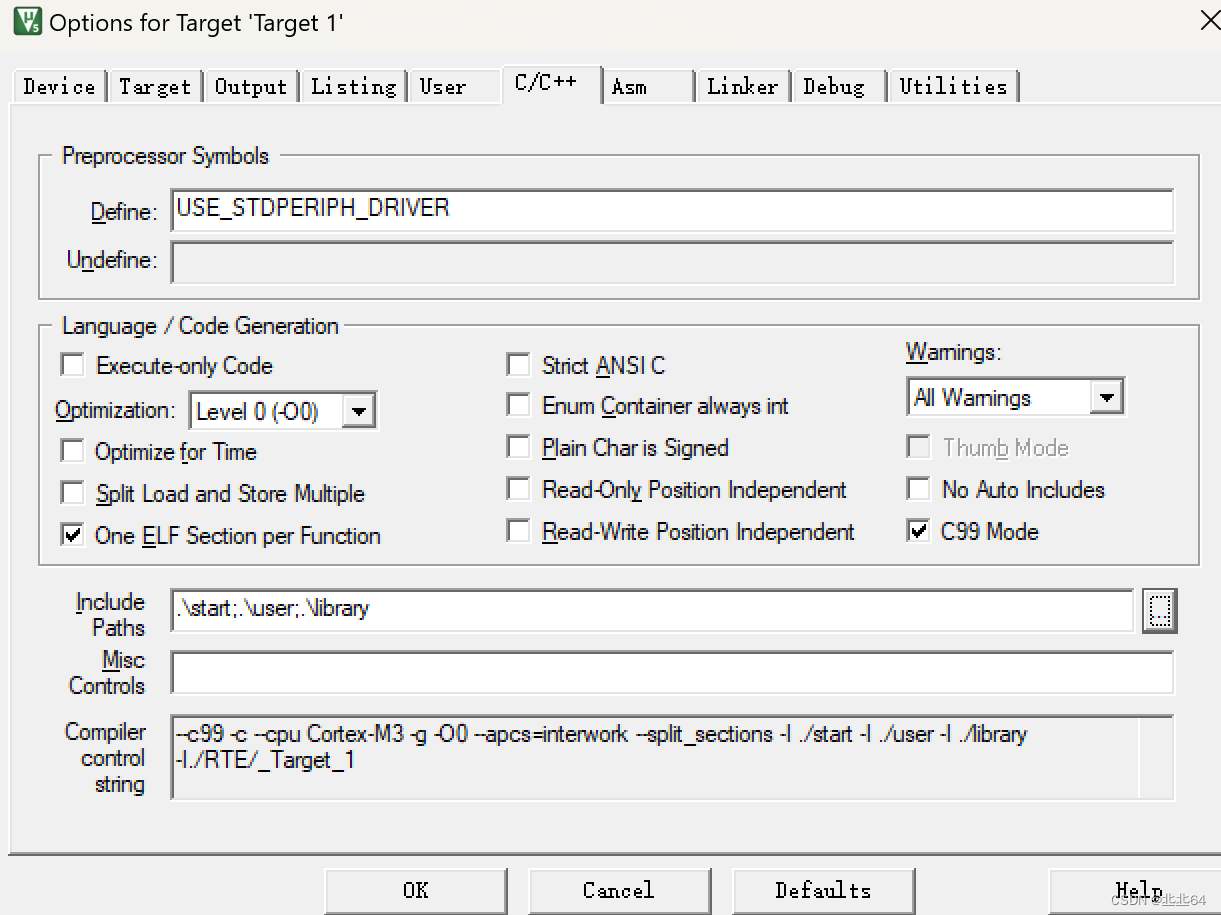
【STM32 |新建一个工程】基于标准库(库函数)新建工程
目录 STM32开发方式 库函数文件夹 建工程步骤 库函数工程建立 建立工程总结 STM32开发方式 目前stm32的开发方式主要有基于寄存器的方式、基于标准库的方式(库函数的方式)、基于HAL库的方式基于库函数的方式是使用ST官方提供的封装好的函数&…...

C#利用ClearScript执行Javascript脚本
1,新建.netframework winform工程 2,打开nuget程序包管理界面,安装Microsoft.ClearScript.V8,Microsoft.ClearScript.V8.Native.win-x64. 3,编写Javascript脚本,另存为demo.js function testFunc(t) {return t "…...

住宅ip与数据中心ip代理的区别是什么
代理通常意味着“替代”。它是用户设备和目标服务器之间的中介,允许在不同的IP地址下上网。代理ip根据来源分类可分住宅ip与数据中心ip,二者之间区别是什么呢? 住宅ip是由互联网服务提供商(ISP)提供给家庭的IP地址。出于这个原因,…...

【计算机网络】数据链路层的功能
数据链路层的基本功能: 封装成帧透明传输差错检测 数据链路层使用的信道主要有两种 点对点信道——PPP协议广播信道——CSMA/CD协议(有线局域网)、CSMA/CA协议(无线局域网) 数据链路层所处的地位 从图中可以看出,数据从主机H1送到主机H2需要在路径中…...

信号线电路串联电阻
简介 两芯片端串联一个电阻,在靠近发送端或接收端。 一般串联的是0Ω, 22Ω, 33Ω的电阻,也可能更大。 目的 1.解决信号反射问题,吸收反射。 问题如下: pcb单端阻抗过大,而接收端是cmos输入,使得接收端…...

手机App防沉迷系统-算法
import java.util.*; public class Main{public static void main(String[] args){Scanner innew Scanner(System.in);int nInteger.parseInt(in.nextLine());//已注册app列表List<Log> listnew ArrayList<>();for(int k0;k<n;k){String[] strin.nextLine().spl…...
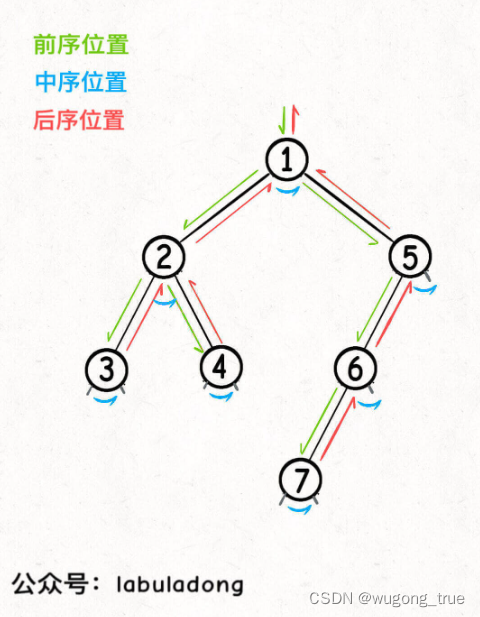
day3_prefixSum
一、前缀和技巧 重点 前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和 个人理解;预计算,空间换时间 1.(一维数组的前缀和)303区域和检索-数组不可变 获取闭区间值 [left,right] -> preSum[right 1] - preSum[left],其中preSum[right…...
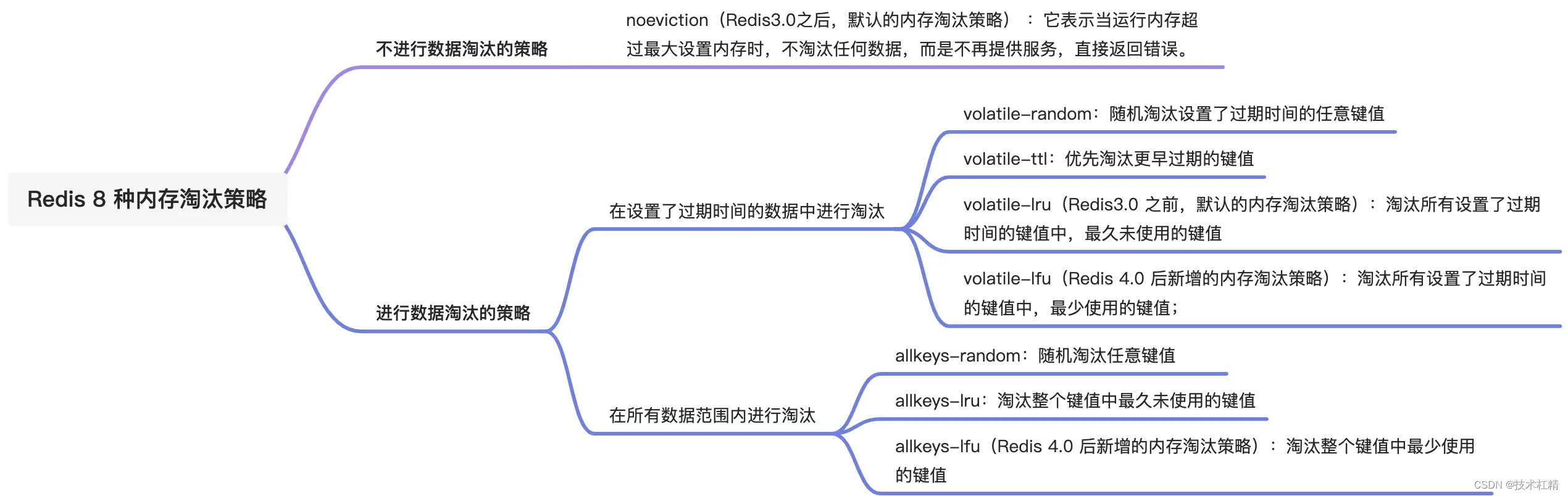
Redis过期删除策略和内存淘汰策略有什么区别?
Redis过期删除策略和内存淘汰策略有什么区别? 前言过期删除策略如何设置过期时间?如何判定 key 已过期了?过期删除策略有哪些?Redis 过期删除策略是什么? 内存淘汰策略如何设置 Redis 最大运行内存?Redis 内…...

【计算机网络】物理层传输介质 习题3
双绞线是用两根绝缘导线绞合而成的,绞合的目的是( )。 A.减少干扰 B.提高传输速度 C.增大传输距离 D.增大抗拉强度 在电缆中采用屏蔽技术带来的好处主要是( ) A.减少信号衰减 B. 减少电磁干扰辐射 C.减少物理损坏 D. 减少电缆的阻抗 利用一根同轴电缆互连主机构成…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
