day3_prefixSum
一、前缀和技巧
重点
前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和
个人理解;预计算,空间换时间
1.(一维数组的前缀和)303区域和检索-数组不可变
获取闭区间值 [left,right] -> preSum[right + 1] - preSum[left],其中preSum[right+1]表示累加到right时的总和
class NumArray {// 前缀和数组private int[] preSum;/* 输入一个数组,构造前缀和 */public NumArray(int[] nums) {// preSum[0] = 0,便于计算累加和preSum = new int[nums.length + 1];// 计算 nums 的累加和for (int i = 1; i < preSum.length; i++) {preSum[i] = preSum[i - 1] + nums[i - 1];}}/* 查询闭区间 [left, right] 的累加和 */public int sumRange(int left, int right) {return preSum[right + 1] - preSum[left];}
}/*** Your NumArray object will be instantiated and called as such:* NumArray obj = new NumArray(nums);* int param_1 = obj.sumRange(left,right);*/
2.(二维数组的前缀和)
同样的预计算
class NumMatrix {
// 定义:preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和private int[][] preSum;public NumMatrix(int[][] matrix) {int m = matrix.length, n = matrix[0].length;if (m == 0 || n == 0) return;// 构造前缀和矩阵preSum = new int[m + 1][n + 1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 计算每个矩阵 [0, 0, i, j] 的元素和preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];}}}// 计算子矩阵 [x1, y1, x2, y2] 的元素和public int sumRegion(int x1, int y1, int x2, int y2) {// 目标矩阵之和由四个相邻矩阵运算获得return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];}
}/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix obj = new NumMatrix(matrix);* int param_1 = obj.sumRegion(row1,col1,row2,col2);*/
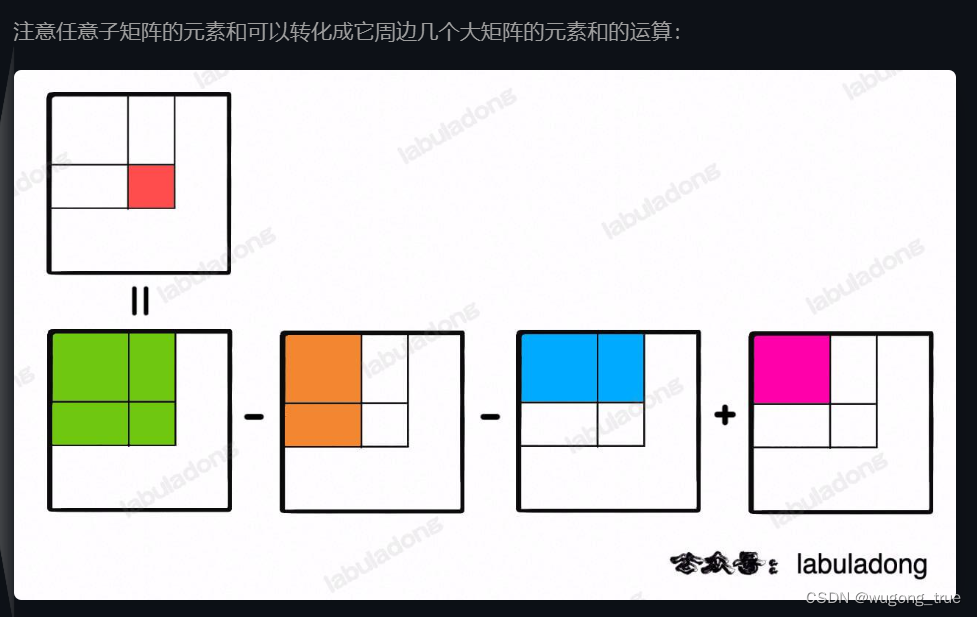
- 任何一个小矩阵可以由上图的矩阵计算得到
- 而下面这四个矩阵对应的是小矩阵的四个顶点(根据参数可推)
- 所以预计算每个以(0,0),(x,y)结尾的矩阵的值,经过计算即可得到
二、二叉树(纲领篇)
参考链接东哥带你刷二叉树(纲领篇) | labuladong 的算法笔记
先在开头总结一下,二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?
如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?
如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
无论使用哪种思维模式,你都需要思考:
如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
1.二叉树的重要性
举个例子,比如两个经典排序算法 快速排序 和 归并排序,对于它俩,你有什么理解?
如果你告诉我,快速排序就是个二叉树的前序遍历,归并排序就是个二叉树的后序遍历,那么我就知道你是个算法高手了。
…
如果你一眼就识破这些排序算法的底细,还需要背这些经典算法吗?不需要。你可以手到擒来,从二叉树遍历框架就能扩展出算法了。
说了这么多,旨在说明,二叉树的算法思想的运用广泛,甚至可以说,只要涉及递归,都可以抽象成二叉树的问题。
2.深入理解前中后序
根据几个问题引发思考
1、你理解的二叉树的前中后序遍历是什么,仅仅是三个顺序不同的 List 吗?
2、请分析,后序遍历有什么特殊之处?
3、请分析,为什么多叉树没有中序遍历?
鄙人是肯定答不上来的
void traverse(TreeNode root) {if (root == null) {return;}// 前序位置traverse(root.left);// 中序位置traverse(root.right);// 后序位置
}你也注意到了,只要是递归形式的遍历,都可以有前序位置和后序位置,分别在递归之前和递归之后。
所谓前序位置,就是刚进入一个节点(元素)的时候,后序位置就是即将离开一个节点(元素)的时候,那么进一步,你把代码写在不同位置,代码执行的时机也不同:
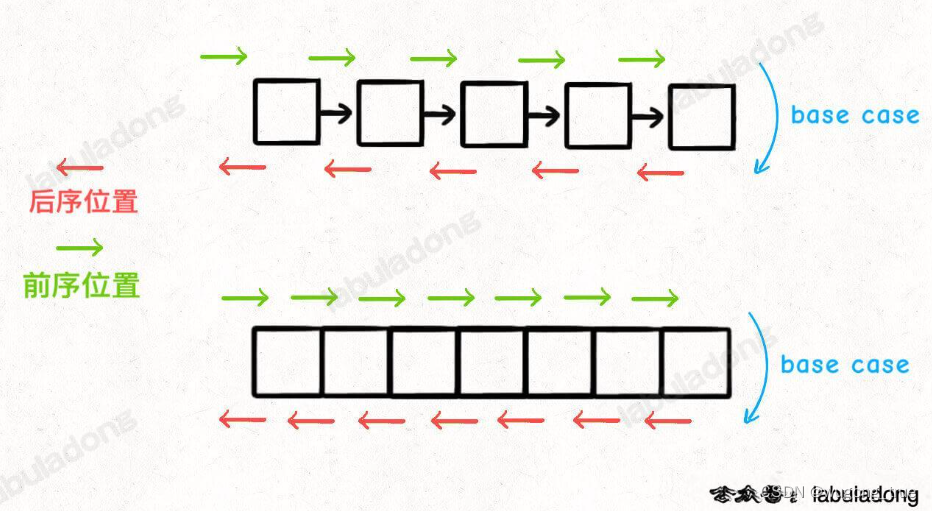
比如说,如果让你倒序打印一条单链表上所有节点的值,你怎么搞?
实现方式当然有很多,但如果你对递归的理解足够透彻,可以利用后序位置来操作
/* 递归遍历单链表,倒序打印链表元素 */
void traverse(ListNode head) {if (head == null) {return;}traverse(head.next);// 后序位置print(head.val);
}教科书里只会问你前中后序遍历结果分别是什么,所以对于一个只上过大学数据结构课程的人来说,他大概以为二叉树的前中后序只不过对应三种顺序不同的 List<Integer> 列表。
但是我想说,前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点,绝不仅仅是三个顺序不同的 List:
- 前序位置的代码在刚刚进入一个二叉树节点的时候执行;
- 后序位置的代码在将要离开一个二叉树节点的时候执行;
- 中序位置的代码在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
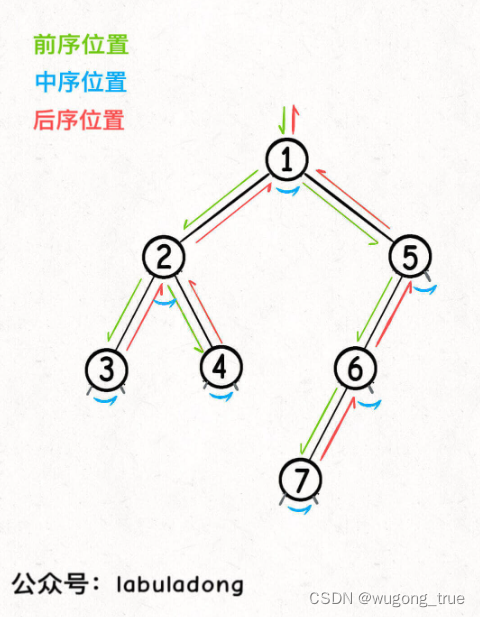
这里你也可以理解为什么多叉树没有中序位置,因为二叉树的每个节点只会进行唯一一次左子树切换右子树,而多叉树节点可能有很多子节点,会多次切换子树去遍历,所以多叉树节点没有「唯一」的中序遍历位置。
重点1
二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的,你只需要单独思考每一个节点应该做什么,其他的不用你管,抛给二叉树遍历框架,递归会在所有节点上做相同的操作。
3.两种解题思路
二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案,这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。

4.后序位置的特殊之处
中序位置主要用在 BST 场景中,你完全可以把 BST 的中序遍历认为是遍历有序数组。
前序位置本身其实没有什么特别的性质,之所以你发现好像很多题都是在前序位置写代码,实际上是因为我们习惯把那些对前中后序位置不敏感的代码写在前序位置罢了。
你可以发现,前序位置的代码执行是自顶向下的,而后序位置的代码执行是自底向上的:
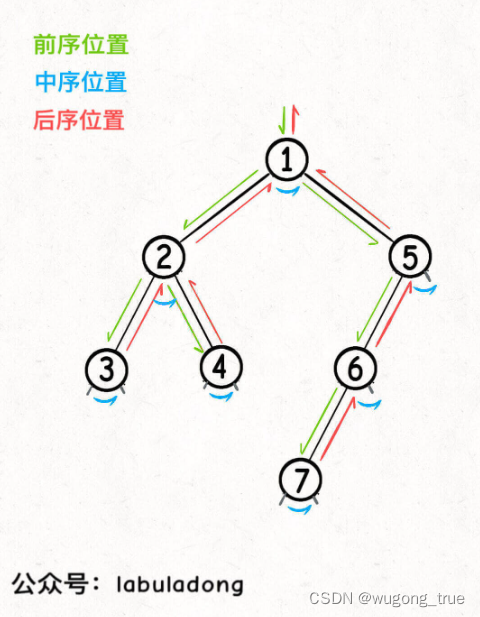
重点2
但这里面大有玄妙,意味着前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
举具体的例子,现在给你一棵二叉树,我问你两个简单的问题:
1、如果把根节点看做第 1 层,如何打印出每一个节点所在的层数?
2、如何打印出每个节点的左右子树各有多少节点?
第一个问题从根节点就能给出答案,而第二个问题必须遍历完子树之后才能给出答案
结合这两个简单的问题,你品味一下后序位置的特点,只有后序位置才能通过返回值获取子树的信息。
那么换句话说,一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了。
例题lc543题 二叉树的直径
5.以树的视角看 动归/回溯/DFS算法的区别和联系
DFS 算法和回溯算法非常类似,只是在细节上有所区别。
这个细节上的差别是什么呢?其实就是「做选择」和「撤销选择」到底在 for 循环外面还是里面的区别,DFS 算法在外面,回溯算法在里面。
为什么有这个区别?还是要结合着二叉树理解。这一部分我就把回溯算法、DFS 算法、动态规划三种经典的算法思想,以及它们和二叉树算法的联系和区别,用一句话来说明:
动归/DFS/回溯算法都可以看做二叉树问题的扩展,只是它们的关注点不同:
- 动态规划算法属于分解问题的思路,它的关注点在整棵「子树」。
- 回溯算法属于遍历的思路,它的关注点在节点间的「树枝」。
- DFS 算法属于遍历的思路,它的关注点在单个「节点」。
三个例子解释三种情况
1.计算一棵二叉树有多少个节点?
// 定义:输入一棵二叉树,返回这棵二叉树的节点总数
int count(TreeNode root) {if (root == null) {return 0;}// 我这个节点关心的是我的两个子树的节点总数分别是多少int leftCount = count(root.left);int rightCount = count(root.right);// 后序位置,左右子树节点数加上自己就是整棵树的节点数return leftCount + rightCount + 1;
}你看,这就是动态规划分解问题的思路,它的着眼点永远是结构相同的整个子问题,类比到二叉树上就是「子树」。
你再看看具体的动态规划问题,比如 动态规划框架套路详解 中举的斐波那契的例子,我们的关注点在一棵棵子树的返回值上:
2.使用遍历的思路写一个traverse函数,打印出遍历这棵二叉树的过程
…
回溯算法遍历的思路,它的着眼点永远是在节点之间移动的过程,类比到二叉树上就是[树枝]
3.把二叉树的每个节点值都+1
void traverse(TreeNode root) {if (root == null) return;// 遍历过的每个节点的值加一root.val++;traverse(root.left);traverse(root.right);
}你看,这就是 DFS 算法遍历的思路,它的着眼点永远是在单一的节点上,类比到二叉树上就是处理每个「节点」。
你再看看具体的 DFS 算法问题,比如 一文秒杀所有岛屿题目 中讲的前几道题,我们的关注点是 grid 数组的每个格子(节点),我们要对遍历过的格子进行一些处理,所以我说是用 DFS 算法解决这几道题的:
有了这些铺垫,你就很容易理解为什么回溯算法和 DFS 算法代码中「做选择」和「撤销选择」的位置不同了,看下面两段代码:
// DFS 算法把「做选择」「撤销选择」的逻辑放在 for 循环外面
void dfs(Node root) {if (root == null) return;// 做选择print("我已经进入节点 %s 啦", root)for (Node child : root.children) {dfs(child);}// 撤销选择print("我将要离开节点 %s 啦", root)
}// 回溯算法把「做选择」「撤销选择」的逻辑放在 for 循环里面
void backtrack(Node root) {if (root == null) return;for (Node child : root.children) {// 做选择print("我站在节点 %s 到节点 %s 的树枝上", root, child)backtrack(child);// 撤销选择print("我将要离开节点 %s 到节点 %s 的树枝上", child, root)}
}看到了吧,你回溯算法必须把「做选择」和「撤销选择」的逻辑放在 for 循环里面,否则怎么拿到「树枝」的两个端点?
6.层序遍历(简单过一下)
二叉树题型主要是用来培养递归思维的,而层序遍历属于迭代遍历,也比较简单,这里就过一下代码框架吧:
// 输入一棵二叉树的根节点,层序遍历这棵二叉树
void levelTraverse(TreeNode root) {if (root == null) return;Queue<TreeNode> q = new LinkedList<>();q.offer(root);// 从上到下遍历二叉树的每一层while (!q.isEmpty()) {int sz = q.size();// 从左到右遍历每一层的每个节点for (int i = 0; i < sz; i++) {TreeNode cur = q.poll();// 将下一层节点放入队列if (cur.left != null) {q.offer(cur.left);}if (cur.right != null) {q.offer(cur.right);}}}
}相关文章:

day3_prefixSum
一、前缀和技巧 重点 前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和 个人理解;预计算,空间换时间 1.(一维数组的前缀和)303区域和检索-数组不可变 获取闭区间值 [left,right] -> preSum[right 1] - preSum[left],其中preSum[right…...
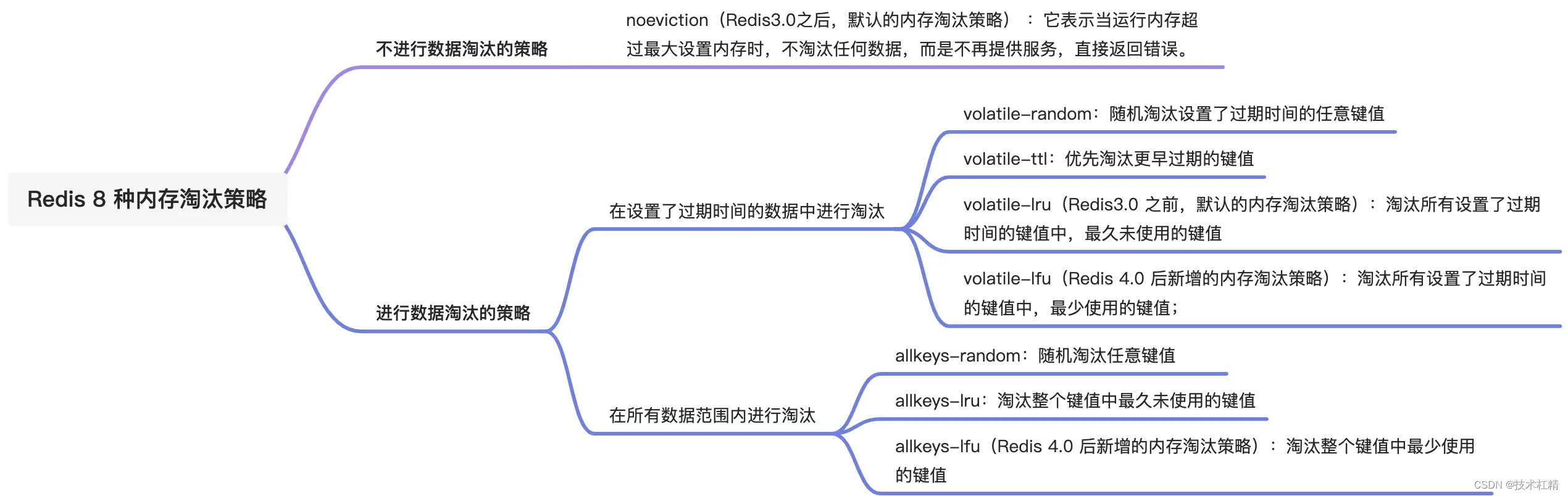
Redis过期删除策略和内存淘汰策略有什么区别?
Redis过期删除策略和内存淘汰策略有什么区别? 前言过期删除策略如何设置过期时间?如何判定 key 已过期了?过期删除策略有哪些?Redis 过期删除策略是什么? 内存淘汰策略如何设置 Redis 最大运行内存?Redis 内…...

【计算机网络】物理层传输介质 习题3
双绞线是用两根绝缘导线绞合而成的,绞合的目的是( )。 A.减少干扰 B.提高传输速度 C.增大传输距离 D.增大抗拉强度 在电缆中采用屏蔽技术带来的好处主要是( ) A.减少信号衰减 B. 减少电磁干扰辐射 C.减少物理损坏 D. 减少电缆的阻抗 利用一根同轴电缆互连主机构成…...

智能座舱语音助手产品方案
一、用户调研与痛点分析 1.目标用户分析 用户画像 性别女性年龄50地域2-3线城市职业退休或退居二线教育中专、 大专、 本科财务家庭财务管理者爱好享受生活、 照顾家庭标签有闲有小钱二、产品定位与卖点提炼 购车目的 愉悦自我, 专属于自己的座驾: 家…...

经典面试题之滑动窗口专题
class Solution { public:int minSubArrayLen(int target, vector<int>& nums) {// 长度最小的子数组 // 大于等于 targetint min_len INT32_MAX;// 总和int sum 0;int start 0; // 起点for(int i 0; i< nums.size(); i) {sum nums[i];while(sum > targe…...

网络编程入门之UDP编程
欢迎各位帅哥美女来捧场,本文是介绍UDP网络编程。在这里,你会见到最详细的教程;细致到每一行代码,每一个api的由来和使用它的目的等。 目录 1.UDP相关API 1.1.两个类 1.2.两个类中的方法 2.UDP编程 2.1.大体框架 2.2.内容构…...

【AI源码】音频和图片生成你的数字人口播
带表情、带头部运动。适合做一些名人短视频鸡汤口播 类似此前微软和阿里emo那个方案 1、介绍: 能够通过单张静态肖像和输入音频生成具有自然流动运动的谈话视频,它采用了一种普遍的运动表示方法,能够捕捉广泛的面部动态,包括细微的表情和头部运动。 2、框架概述 (1)该…...

JAVA_3
JAVA_3 一、JAVA类和对象二、JAVA内存如何运转三、JAVA-constructer 一、JAVA类和对象 类包含三个内容: 1.属性field,静态特征(数据) 2.方法method,负责动态行为操作数据 3.构造器constructer,负责初始化对象…...

java项目之汽车资讯网站源码(springboot+mysql+vue)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的汽车资讯网站。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 汽车资讯网站的主要使用者管…...

C语言中的静态库和动态库的制作和使用
什么是库文件 单一模型 将程序中所有功能全部实现于一个单一的源文件内部。 编译时间长,不易于维护和升级,不易于协作开发。 分离模型 将程序中的不同的功能模块划分到不同的源文件中。 缩短编译时间,易于维护和升级,易于协…...
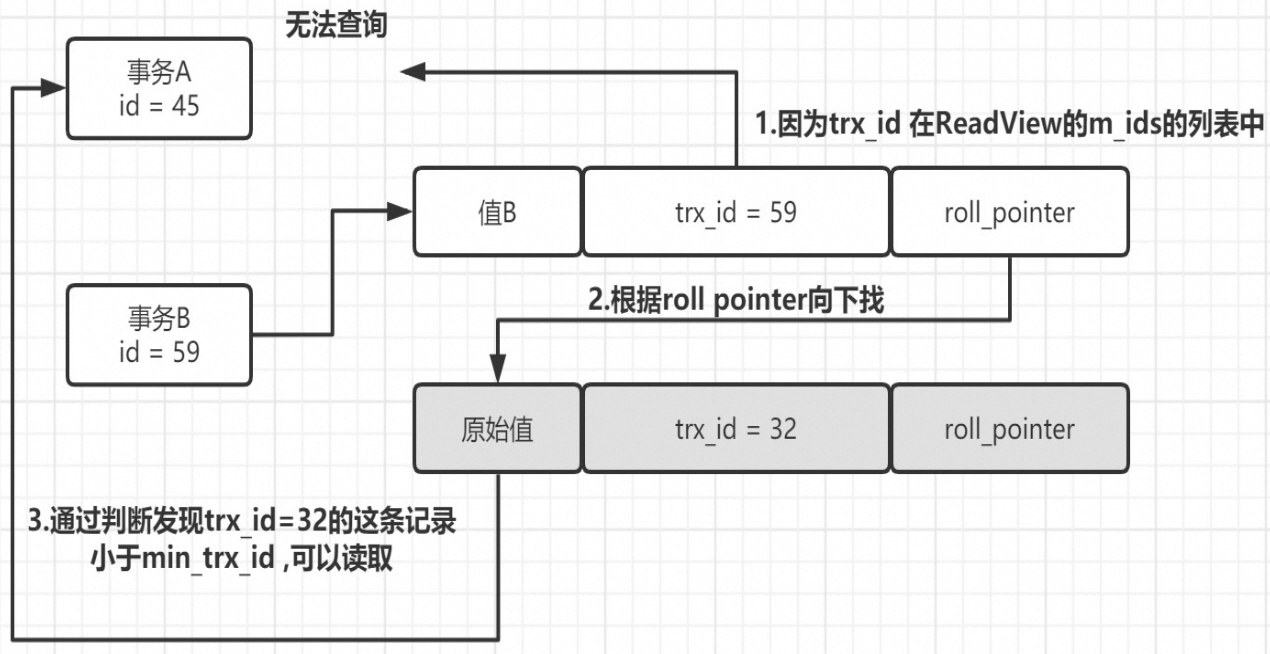
【MySQL 数据宝典】【事务锁】- 002 事务控制的演进
一、事务处理思路 1.1 排队 排队处理是事务管理最简单的方法,就是完全顺序执行所有事务的数据库操作,不需要加锁,简单的说就是全局排队。序列化执行所有的事务单元,数据库某个时刻只处理一个事务操作,特点是强一致性…...

如何远程操作服务器中的Python编译器并将运行结果返回到Pycharm
文章目录 一、前期准备1. 检查IDE版本是否支持2. 服务器需要开通SSH服务 二、Pycharm本地链接服务器测试1. 配置服务器python解释器 三、使用内网穿透实现异地链接服务器开发1. 服务器安装Cpolar2. 创建远程连接公网地址 四、使用固定TCP地址远程开发 本文主要介绍如何使用Pych…...

C++入门指南(上)
目录 编辑 一、祖师爷画像 二、什么是C 三、C发展史 四、C在工作领域的应用 1. 操作系统以及大型系统软件开发 2. 服务器端开发 3. 游戏开发 4. 嵌入式和物联网领域 5. 数字图像处理 6. 人工智能 7. 分布式应用 五、如何快速上手C 一、祖师爷画像 本贾尼斯特劳斯…...

Python 全栈系列244 nginx upstream 负载均衡 踩坑日记
说明 最初是因为租用算力机(Python 全栈系列242 踩坑记录:租用算力机完成任务),所以想着做一个负载均衡,然后多开一些服务,把配置写在nginx里面就好了。 一开始租用了一个3080起了一个服务,后来觉得速度不够快,再起了…...

数据链路层——计算机网络学习笔记三
使用点对点信道的数据链路层 前言: 1.数据链路层的重要性:网络中的主机、路由器都必须实现数据连输层; 2.数据链路层中使用的信道: 点对点信道:这种信道是一对一的通信方式; 广播信道:使用一对多…...
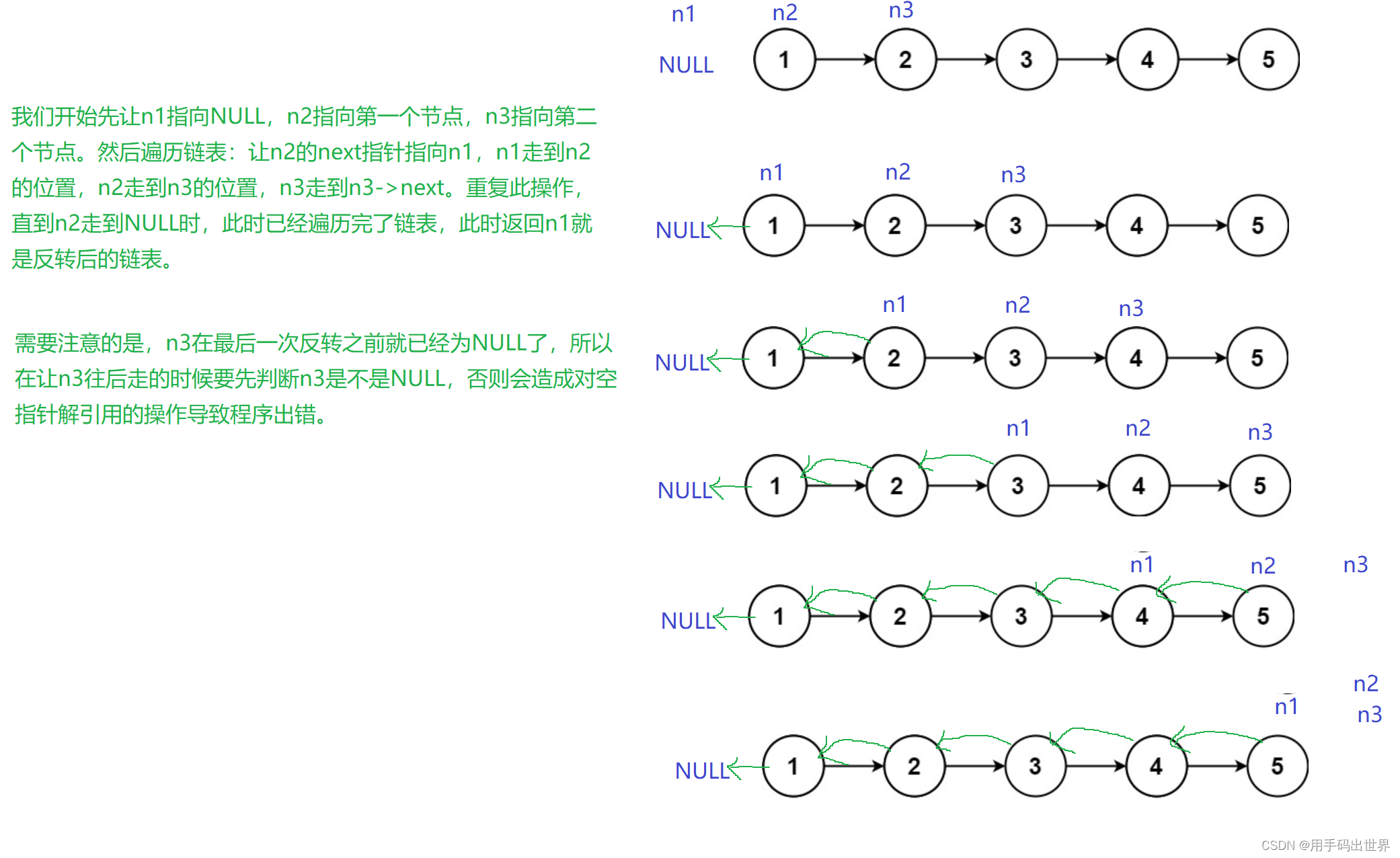
leetcode——反转链表
206. 反转链表 - 力扣(LeetCode) 思路:创建三个指针n1,n2,n3,遍历原链表,通过三者之间的关系将链表反转。下面给出图示: 下面给出题解代码: typedef struct ListNode ListNode; struct List…...

类加载机制(双亲委派机制)
文章目录 JVM的作用是什么双亲委派机制加载流程 JVM的作用是什么 我们运行Java程序时,要安装JDK,JDK包含JVM,不同环境的JDK都是不同的。 Java 代码在编译后会形成 class 的字节码文件,该字节码文件通过 JVM 解释器,生…...

nss刷题(2)
1、[NSSCTF 2022 Spring Recruit]ezgame 打开题目是一个游戏界面 发现是有分数的,猜测分数达到某个之后可以获得flag,查看源码看一下 看到末尾显示分数超过65后显示flag 在js中找到了一个score,将他的值改为大于65的数后随意玩一次就可以得到flag同时&a…...
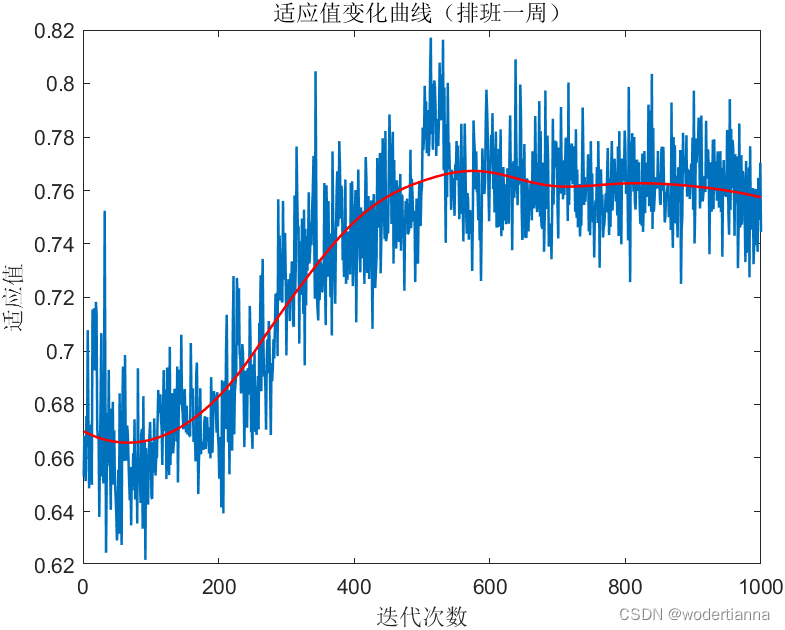
2024 年“泰迪杯”A 题:生产线的故障自动识别与人员配置--第四题(用遗传算法解决生产线排班问题--matlab代码)
问题背景: 问题四:根据实际情况,现需要扩大生产规模,将生产线每天的运行时间从 8 小时增加 到 24 小时不间断生产,考虑生产线与操作人员的搭配,制定最佳的操作人员排班方案,要求满足以下条件&am…...
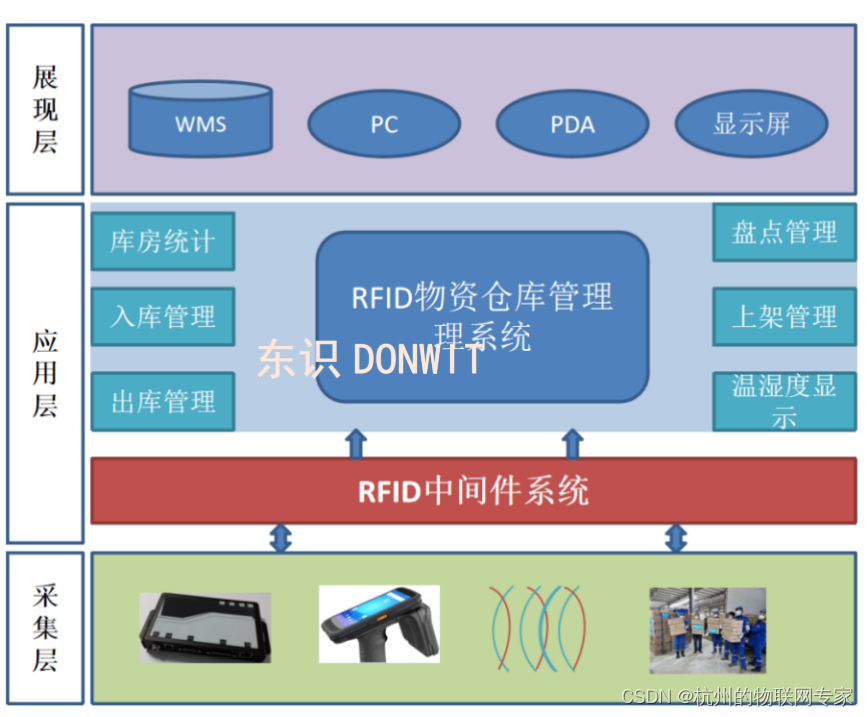
资产公物仓管理系统|实现国有资产智能化管理
1、项目背景 资产公物仓管理系统(智仓库DW-S201)是一套成熟系统,依托互3D技术、云计算、大数据、RFID技术、数据库技术、AI、视频分析技术对RFID智能仓库进行统一管理、分析的信息化、智能化、规范化的系统。 项目设计原则 方案对公物仓资…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
