动态规划----股票买卖问题(详解)
目录
一.买卖股票的最佳时机:
二.买卖股票的最佳时机含冷冻期:
三.买卖股票的最佳时期含⼿续费:
四.买卖股票的最佳时机III:
五.买卖股票的最佳时机IV:
买卖股票的最佳时机问题介绍:动态规划买卖股票的最佳时机是一个经典的算法问题。该问题的目标是在给定的股票价格数组中,找到最大的利润,即最佳的买入和卖出时间,使得买入时间早于卖出时间。
下面我们通过一些例题,来解决这一类动态规划的问题:
一.买卖股票的最佳时机:
- 题目链接:121. 买卖股票的最佳时机 - 力扣(LeetCode)
- 题目描述:
给定一个数组
prices,它的第i个元素prices[i]表示一支给定股票第i天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回
0。

①.动态规划解法:
- 一.状态表示dp[ i ][ j ]:下标为
i这一天结束的时候,手上持股状态为j时,我们持有的最大利润。这里我们定义状态 j (两种情况)分别为:- 0 买入状态
- 1 可交易状态
- 二.状态转移方程:
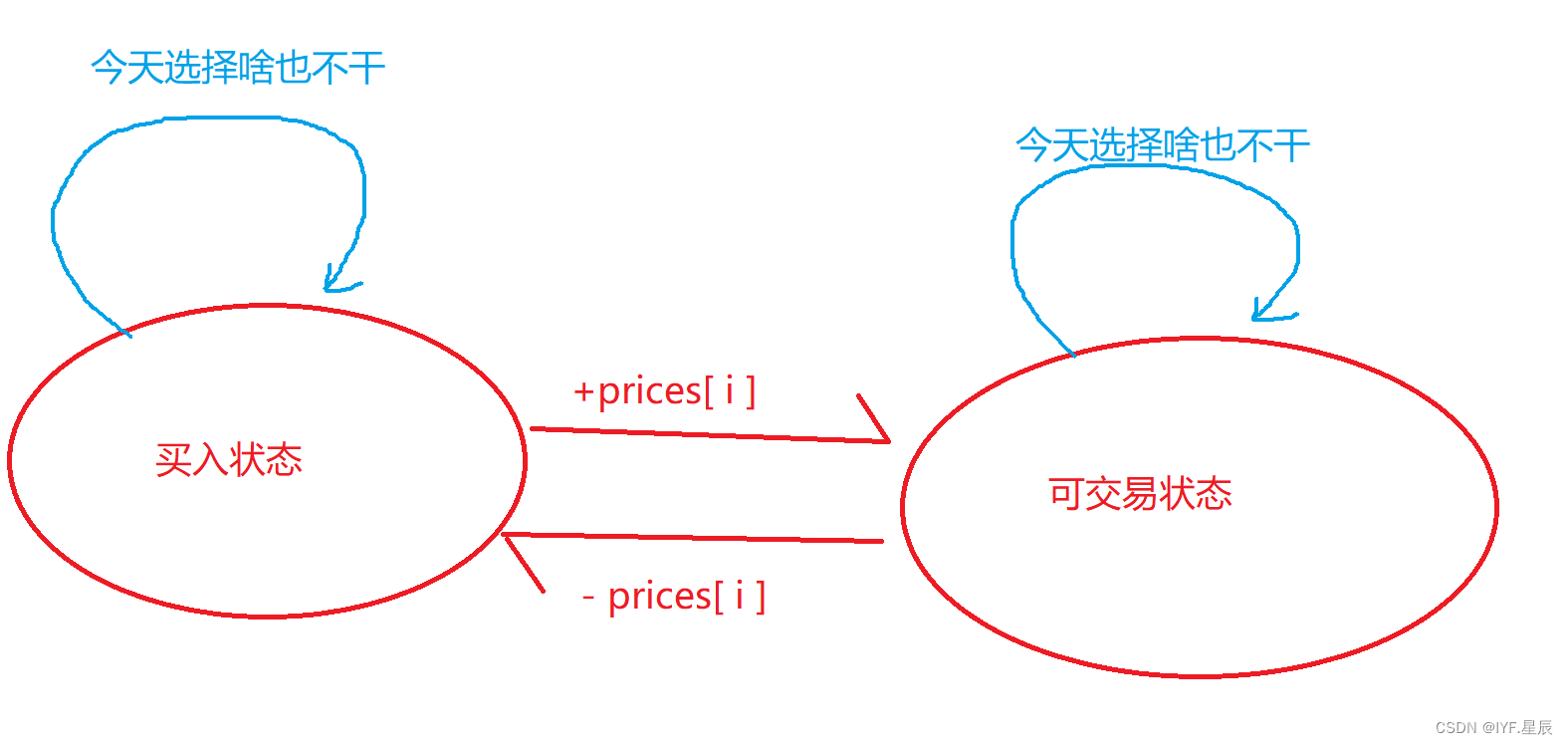
- dp[ i ][ 0 ] = Math.max( dp[ i - 1 ][ 0 ], -prices[ i ]) ; ①.在前面一天已经是买入状态,今天选择什么也不干,今天结束后,是买入状态。②.前面是可交易状态,今天选择买入,则今天结束后是买入状态,这里注意不是dp[ i - 1][ 1 ] - prices[ i ];因为只能交易一次,如果今天选择买入,那后面一定要卖出(这算一次交易),此时才可能有最大利润。则前面不能有交易,利润为0.
- dp[ i ][ 1 ] = Math.max( dp[ i - 1][ 1 ],dp[ i - 1][ 0 ] + prices[ i ]);①.前面一天是可交易状态,今天选择什么也不干,今天结束后是可交易状态。②.前面一天是买入状态,今天选择卖出,今天结束后是可交易状态。
- 三.初始化:根据状态表示:
- dp[ 0 ][ 0 ] = - prices[ 0 ];第一天选择买入,此时利润为 - prices[ 0 ]
- dp[ 0 ][ 1 ] = 0;第一天选择什么也不干或则交易一次,此时的利润为0;
- 四.填表顺序:根据状态转移方程,从左往右,从上往下填写.
- 五.返回值:dp[ n - 1 ][ 1 ];n为prices数组的长度,最后一天结束后,是可交易状态,此时为最大利润.
各个状态关系图:
代码详解:
class Solution {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][2];//初始化dp[0][0] = -prices[0];dp[0][1] = 0;for(int i = 1;i < n;i++){//注意这里不是dp[i - 1][1] - prices[i];dp[i][0] = Math.max(dp[i - 1][0], - prices[i]);dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][0] + prices[i]);}//返回值return dp[n - 1][1];} }
②.暴力解法(相对简单这里给出解题过程): 
代码详解:
class Solution {public int maxProfit(int[] prices) {int cost = Integer.MAX_VALUE;int profit = 0;for(int price : prices){cost = Math.min(cost,price);profit = Math.max(profit,price - cost);}return profit;}
}运行结果:
二.买卖股票的最佳时机含冷冻期:
- 题目链接:309. 买卖股票的最佳时机含冷冻期 - 力扣(LeetCode)
- 问题描述:
给定一个整数数组
prices,其中第prices[i]表示第i天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
-
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
-
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。

动态规划解法:
一.状态表示:dp[ i ][ j ]:由于有「买⼊」「可交易」「冷冻期」三个状态,因此我们可以选择⽤三个数组,其中:
- dp[i][0] 表⽰:第 i 天结束后,处于「买⼊」状态,此时的最⼤利润;
- dp[i][1] 表⽰:第 i 天结束后,处于「可交易」状态,此时的最⼤利润;
- dp[i][2] 表⽰:第 i 天结束后,处于「冷冻期」状态,此时的最⼤利润
二.状态转移方程:
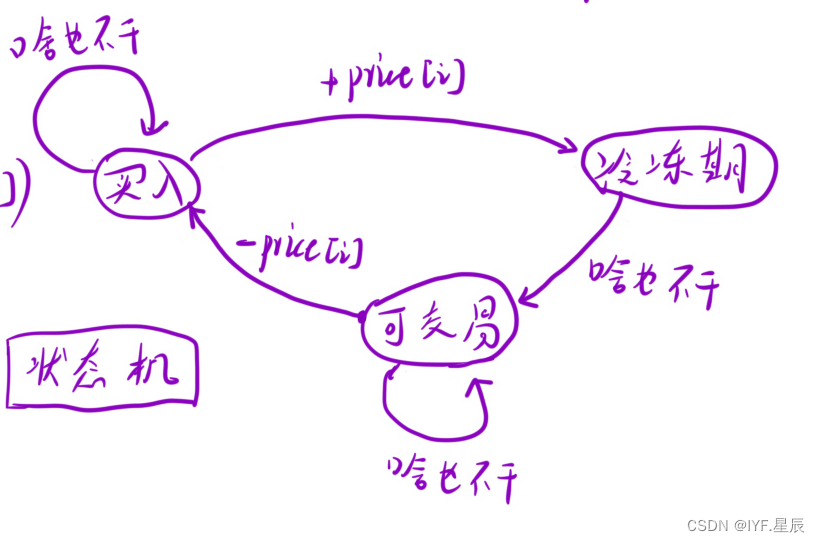
- dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); ①.前一天是买入状态,今天啥也不做,今天结束后是买入状态②.前面一天是可交易状态,今天选择买入,今天结束后是买入状态。
- dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]); ①.前面一天是可交易状态,今天啥也不干,今天结束后是可交易状态②.前面一天是冷冻期,今天啥也不干,今天过后是可交易状态
- dp[i][2] = dp[i - 1][0] + prices[i];前面一天是买入状态,今天选择卖出,今天过后是冷冻期
三.初始化:
dp[0][0] = - prices[0] ; dp[0][1] = 0 ; dp[0][2] = 0;
四.填表顺序:从左往右,从上往下,依次填写三个表
五.返回值:状态转移方程三者的最大值:
max(dp[n - 1][1], dp[n - 1] [2]);dp[n - 1][0]不可能是最大值,这里不用考虑进去(如果考虑进去了也没关系)
各个状态关系图:
代码详解:
class Solution {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值public int maxProfit(int[] prices) {int n = prices.length;int[][] dp = new int[n][3];dp[0][0] = -prices[0];for(int i = 1;i < n;i++){dp[i][0] = Math.max(dp[i - 1][0],dp[i - 1][1] - prices[i]);dp[i][1] = Math.max(dp[i - 1][1],dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return Math.max(dp[n - 1][1],dp[n - 1][2]);} }
运行结果:

三.买卖股票的最佳时期含⼿续费:
题目链接:714. 买卖股票的最佳时机含手续费 - 力扣(LeetCode)
题目描述:
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。

动态规划解法:
一.状态表示:由于有「买⼊」「可交易」两个状态,因此我们可以选择⽤两个数组来定义我们的状态(或则一个二维数组也行),其中:
- f[i] 表⽰:第 i 天结束后,处于「买⼊」状态,此时的最⼤利润;
- g[i] 表⽰:第 i 天结束后,处于「卖出」状态,此时的最⼤利润.
二.状态转移方程 :我们选择在「卖出」的时候,⽀付这个⼿续费,那么在「买⼊」的时候,就不⽤再考虑⼿续费的问题(完成一次交易支付手续费):
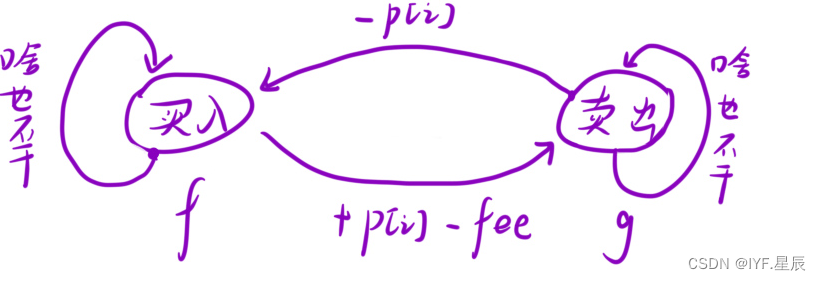
- f[i] = max(f[i - 1], g[i - 1] - prices[i]) ;①.在 i - 1 天「持有」股票,第 i 天啥也不⼲。此时最⼤收益为 f[i - 1] ;②.在 i - 1 天的时候「没有」股票,在第 i 天买⼊股票。此时最⼤收益为 g[i - 1] - prices[i]) ;
- g[i] = max(g[i - 1], f[i - 1] + prices[i] - fee);①.在 i - 1 天「持有」股票,但是在第 i 天将股票卖出。此时最⼤收益为: f[i - 1] + prices[i] - fee) ,记得⼿续费;②.在 i - 1 天「没有」股票,然后第 i 天啥也不⼲。此时最⼤收益为: g[i - 1]
三.初始化:由于需要⽤到前⾯的状态,因此需要初始化第⼀个位置:
- 对于 f[0] ,此时处于「买⼊」状态,因此 f[0] = -prices[0]
- 对于 g[0] ,此时处于「没有股票」状态,啥也不⼲即可获得最⼤收益,因此 g[0] = 0
四.填表顺序:从左到右两个表一起填
五.返回值:应该返回「卖出」状态下,最后⼀天的最⼤值收益: g[n - 1]
代码详解:
class Solution {public int maxProfit(int[] prices, int fee) {int n = prices.length;int[] f = new int[n];int[] g = new int[n];f[0] = -prices[0];for(int i = 1;i < n;i++){f[i] = Math.max(f[i - 1],g[i - 1] - prices[i]);g[i] = Math.max(g[i - 1],f[i - 1] + prices[i] - fee);}return Math.max(f[n - 1],g[n - 1]);} }
运行结果:
四.买卖股票的最佳时机III:
题目链接:123. 买卖股票的最佳时机 III - 力扣(LeetCode)
题目描述:
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。

动态规划解法:
一.状态表示:由于有「买⼊」「可交易」两个状态,因此我们可以选择⽤两个数组。但是这道题⾥⾯还有交易次 数的限制,因此我们还需要再加上⼀维,⽤来表⽰交易次数。其中:
- f[i][j] 表⽰:第 i 天结束后,完成了 j 次交易,处于「买⼊」状态,此时的最⼤利 润;
- g[i][j] 表⽰:第 i 天结束后,完成了 j 次交易,处于「卖出」状态,此时的最⼤利 润。
二.状态转移方程:
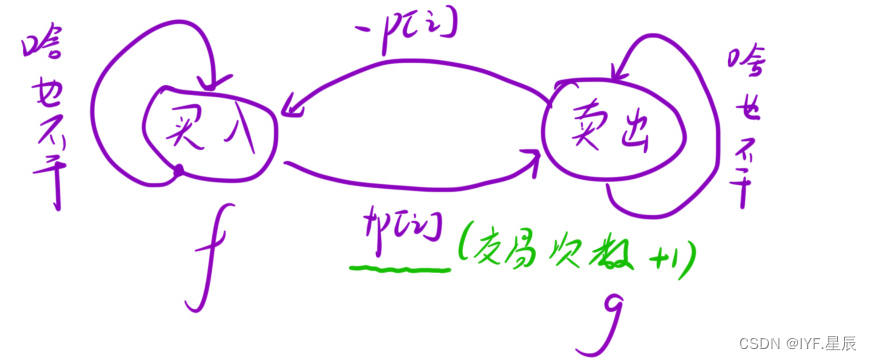
- f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);①.在 i - 1 天的时候,交易了 j 次,处于「买⼊」状态,第 i 天啥也不⼲即可。此时最 ⼤利润为: f[i - 1][j] ;②.在 i - 1 天的时候,交易了 j 次,处于「卖出」状态,第 i 天的时候把股票买了。此 时的最⼤利润为: g[i - 1][j] - prices[i] 。
- g[i][j] = g[i - 1][j];
if(j > 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
①.在 i - 1 天的时候,交易了 j 次,处于「卖出」状态,第 i 天啥也不⼲即可。此时的 最 ⼤利润为: g[i - 1][j] ;
②.在 i - 1 天的时候,交易了 j - 1 次,处于「买⼊」状态,第 i 天把股票卖了,然 后就完 成了 j ⽐交易。此时的最⼤利润为: f[i - 1][j - 1] + prices[i] 。但 是这个状态不⼀定存 在,要先判断⼀下。
三.初始化:
- 当处于第 0 天的时候,只能处于「买⼊过⼀次」的状态,此时的收益为 -prices[0] ,因 此 f[0][0] = - prices[0] 。
- 为了取 max 的时候,⼀些不存在的状态「起不到⼲扰」的作⽤,我们统统将它们初始化为 - INF (⽤ INT_MIN 在计算过程中会有「溢出」的⻛险,这⾥ INF 折半取 0x3f3f3f3f ,⾜够⼩即可)
四.填表顺序:从「上往下填」每⼀⾏,每⼀⾏「从左往右」,两个表「⼀起填」。
五.返回值:返回处于「卖出状态」的最⼤值,但是我们也「不知道是交易了⼏次」,因此返回 g 表最后⼀⾏ 的最⼤值。
代码详解:
class Solution {static int INF = -0x3f3f3f3f;public int maxProfit(int[] prices) {int n = prices.length;int[][] f = new int[n][3];int[][] g = new int[n][3];//1.f[0][0] = -prices[0];for(int i = 1;i < f[0].length;i++){f[0][i] = INF;}for(int j = 1;j < g[0].length;j++){g[0][j] = INF;//Integer.MIN_VALUE/2}//2.for(int i = 1;i < n;i++){for(int j = 0;j < 3;j++){f[i][j] = Math.max(f[i - 1][j],g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j > 0){g[i][j] = Math.max(g[i][j],f[i - 1][j - 1] + prices[i]);}}}int res = Integer.MIN_VALUE;for(int j = 0;j < 3;j++){ res = Math.max(res,g[n - 1][j]);}return res;} }
运行结果:

五.买卖股票的最佳时机IV:
题目链接:188. 买卖股票的最佳时机 IV - 力扣(LeetCode)
题目描述:
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。

动态规划解法:
一.状态表示:为了更加清晰的区分「买⼊」和「卖出」,我们换成「有股票」和「⽆股票」两个状态:
- f[i][j] 表⽰:第 i 天结束后,完成了 j 笔交易,此时处于「有股票」状态的最⼤收益;
- g[i][j] 表⽰:第 i 天结束后,完成了 j 笔交易,此时处于「⽆股票」状态的最⼤收益
二.状态转移方程:
- f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);①.在 i - 1 天的时候,⼿⾥「有股票」,并且交易了 j 次。在第 i 天的时候,啥也不⼲。 此时的收益为 f[i - 1][j] ;②.在 i - 1 天的时候,⼿⾥「没有股票」,并且交易了 j 次。在第 i 天的时候,买了股 票。那么 i 天结束之后,我们就有股票了。此时的收益为 g[i - 1][j] - prices[i];
- g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] + prices[i]);①.在 i - 1 天的时候,⼿⾥「没有股票」,并且交易了 j 次。在第 i 天的时候,啥也不 ⼲。此时的收益为 g[i - 1][j] ;②.在 i - 1 天的时候,⼿⾥「有股票」,并且交易了 j - 1 次。在第 i 天的时候,把 股票卖了。那么 i 天结束之后,我们就交易了 j 次。此时的收益为 f[i - 1][j - 1] + prices[i] ;
三.初始化:
- 当处于第 0 天的时候,只能处于「买⼊过⼀次」的状态,此时的收益为 -prices[0] ,因 此 f[0][0] = - prices[0]
- 为了取 max 的时候,⼀些不存在的状态「起不到⼲扰」的作⽤,我们统统将它们初始化为 - INF (⽤ INT_MIN 在计算过程中会有「溢出」的⻛险,这⾥ INF 折半取 0x3f3f3f3f ,⾜够⼩即可)
四.填表顺序:从上往下填每⼀⾏,每⼀⾏从左往右,两个表⼀起填。
五.返回值:返回处于卖出状态的最⼤值,但是我们也不知道是交易了⼏次,因此返回 g 表最后⼀⾏的最⼤ 值
代码详解:
class Solution {static int INF = -0x3f3f3f3f;public int maxProfit(int k, int[] prices) {int n = prices.length;int[][] f = new int[n][k + 1];int[][] g = new int[n][k + 1];//1.f[0][0] = -prices[0];for(int i = 1;i < f[0].length;i++){f[0][i] = INF;//->防止越界g[i - 1][j] - prices[i];}for(int j = 1;j < g[0].length;j++){g[0][j] = INF;//Integer.MIN_VALUE/2}//2.for(int i = 1;i < n;i++){for(int j = 0;j < k + 1;j++){f[i][j] = Math.max(f[i - 1][j],g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if(j > 0){g[i][j] = Math.max(g[i][j],f[i - 1][j - 1] + prices[i]);}}}int res = Integer.MIN_VALUE;for(int j = 0;j < k + 1;j++){ res = Math.max(res,g[n - 1][j]);}return res;} }
运行结果:

结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!

相关文章:

动态规划----股票买卖问题(详解)
目录 一.买卖股票的最佳时机: 二.买卖股票的最佳时机含冷冻期: 三.买卖股票的最佳时期含⼿续费: 四.买卖股票的最佳时机III: 五.买卖股票的最佳时机IV: 买卖股票的最佳时机问题介绍:动态规划买卖股票的最佳时机是一个经典的…...

Unity射线检测不到MeshCollider的原因
当我们构建的模型是单面模型时,就会出现射线检测不到MeshCollider的问题,对于渲染,我们可以Cull Off来实现双面渲染,而在射线检测时,Unity提供了一个API来控制是否检测背面:Physics.queriesHitBackfaces 案…...
ssrf初步
一,简介 全称:Server-Side Request Forgery(中文:服务器端请求伪造) 攻击者从服务端发起请求,让服务器连接任意外部系统,从而泄露敏感数据。主要利用各种协议的请求伪造,例如php协…...

linux 安装 mangodb 并设置服务开机自启
1、下载 wget http://mosquitto.org/files/source/mosquitto-1.6.8.tar.gz 2、解压 tar -zxvf mosquitto-1.6.8.tar.gz 3、编译安装cd mosquitto-1.6.8 make sudo make install4、在当前目录。进入mosquitto服务文件存放的文件夹 cd service/systemd可以看到3个文件 点击read…...
Virtualbox7.0.10+Ubuntu20.04网络配置
虚拟机部署在服务器上时,需要进行网络配置,使虚拟机和服务器在同网段下,以保证内网的终端可以访问到虚拟机 1. 设置虚拟机 打开虚拟机设置,选择“网络”,将网卡设为桥接网卡 注:设置前,需要先…...

设计模式之服务定位器模式
想象一下,你的Java应用是一座庞大的迷宫,里面藏着无数宝贵的服务宝藏,而你正需要一张精确的藏宝图来指引方向,迅速找到并利用这些宝藏。服务定位器模式,正是这样一张神奇的地图,它帮你动态定位并获取应用中…...
冯喜运:5.12黄金回撤继续上涨,下周原油走势分析
【黄金消息面分析】:本周,黄金市场迎来了自4月中旬以来的最佳单周表现。周五(3月9日),金价攀升至2360.54美元/盎司,涨幅0.62%,而纽约商品交易所6月交割的黄金期货价格上涨1.5%,收报2…...
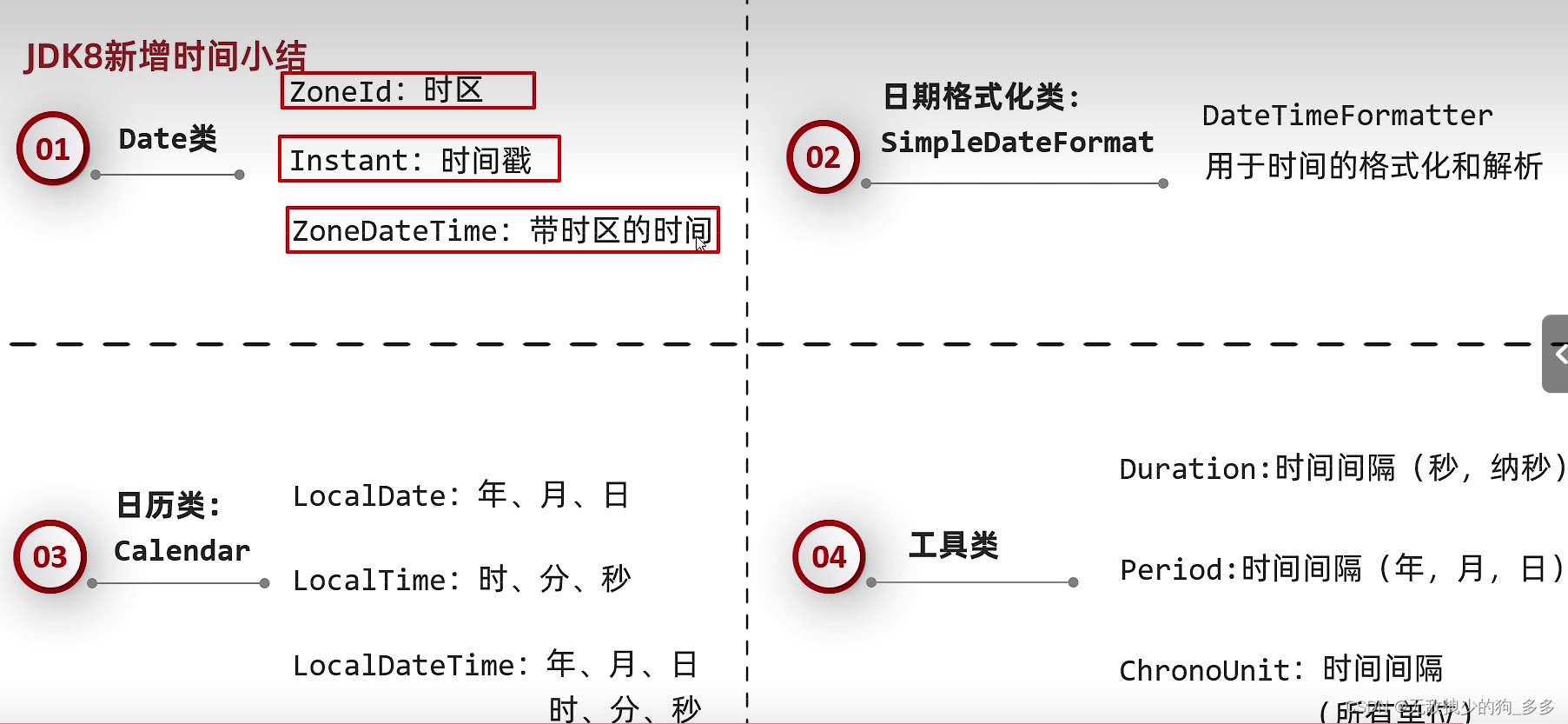
JavaEE企业级开发中常用的JDK7和JDK8的时间类
JDK7时间类 全世界的时间有一个统一的计算标准 在同一条经线上的时间是一样的 格林威治时间 简称GMT 计算核心 地球自转一天是24小时 太阳直射正好是12小时 但是误差太大 现在用原子钟来代替 用铯原子震动的频率来计算时间,作为世界的标准时间UTC 中国标准时间…...

leetcode 2316.统计无向图中无法互相到达点对数
思路:并查集 其实就是连通块的一个变形题目,一般的连通块题目要我们求的是连通个数,或者能不能到达,这里反过来问了。 首先,我们用dfs也是可以做到的,在dfs中统计每一个连通块的个数,然后用乘…...

WPS二次开发系列:如何使用WPS返回的FileUri
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 目录 什么是FileUri 在SDK中的使用场景 打开文档时…...

python删除一个文件夹所有文件
在Python中,可以使用os模块来删除一个文件夹中的所有文件,但保留文件夹本身。以下是一个简单的例子: import osdef delete_files_in_folder(folder_path):for filename in os.listdir(folder_path):file_path os.path.join(folder_path, fi…...

overflow:hidden对解决外边距塌陷的个人理解
外边距塌陷: 子元素的上外边距大于父元素的上外边距,导致边距折叠,取两者之间最大值,即子元素外边距,导致父元素上外边距失效。 解决办法:在父元素样式添加overflow:hidden;或者border:1px solid black;(不…...

【linux软件基础知识】- 文件的概念:Linux 中的文件
Linux 中的文件 在 Linux 中,文件是存储在存储设备(例如硬盘驱动器或固态驱动器)上的数据项的集合。 文件被组织为字节序列,并由文件系统中的唯一名称来标识。 以下是 Linux 中文件的一些关键特征: 字节序列:Linux 中的文件被视为字节序列。 每个字节可以表示一个字符…...
Context capture/Pix4Dmapper/AutoCAD/CASS/EPS软件的安装流程与使用方法;土方量计算;无人机摄影测量数据处理
目录 专题一 无人机摄影测量技术应用现状及其发展 专题二 基本原理和关键技术讲解 专题三 无人机影像外业数据获取 专题四 数据处理环境建立与软件熟悉 专题五 GNSS数据土方量计算 专题六 基于无人机影像数据的正射影像制作 专题七 基于无人机影像数据的三维模型制作 专…...

算法系列之堆排序实践哪家强
1.概念 堆排序是一种树形选择排序,是对简单选择排序的有效改进和优化。 堆(heap),这里所说的堆是数据结构中的堆(对应于算法),而不是内存模型中的堆(数据存储形式,还比如:栈&#…...

01-win10安装Qt5
Qt5安装教程 下载Qt5官网下载(下载很慢)镜像网站下载(有些版本没有资源)迅雷下载(推荐)百度网盘下载(推荐)安装Qt5下载Qt5 官网下载(下载很慢) 【注意】:官网下载非常慢,没有镜像下载时常20+ Qt 官网有一个专门的资源下载网站,所有的开发环境和相关工具都可以从这…...

mybatis使用及配置相关,仅做个人记录
在spring-boot项目中mybatis的配置文件在yml文件中,并没有mybatisconfig.xml文件 yml文件中配置:(来源:https://blog.51cto.com/u_16213723/8747999) mybatis:# XML文件路径,可配置多个,逗号分…...
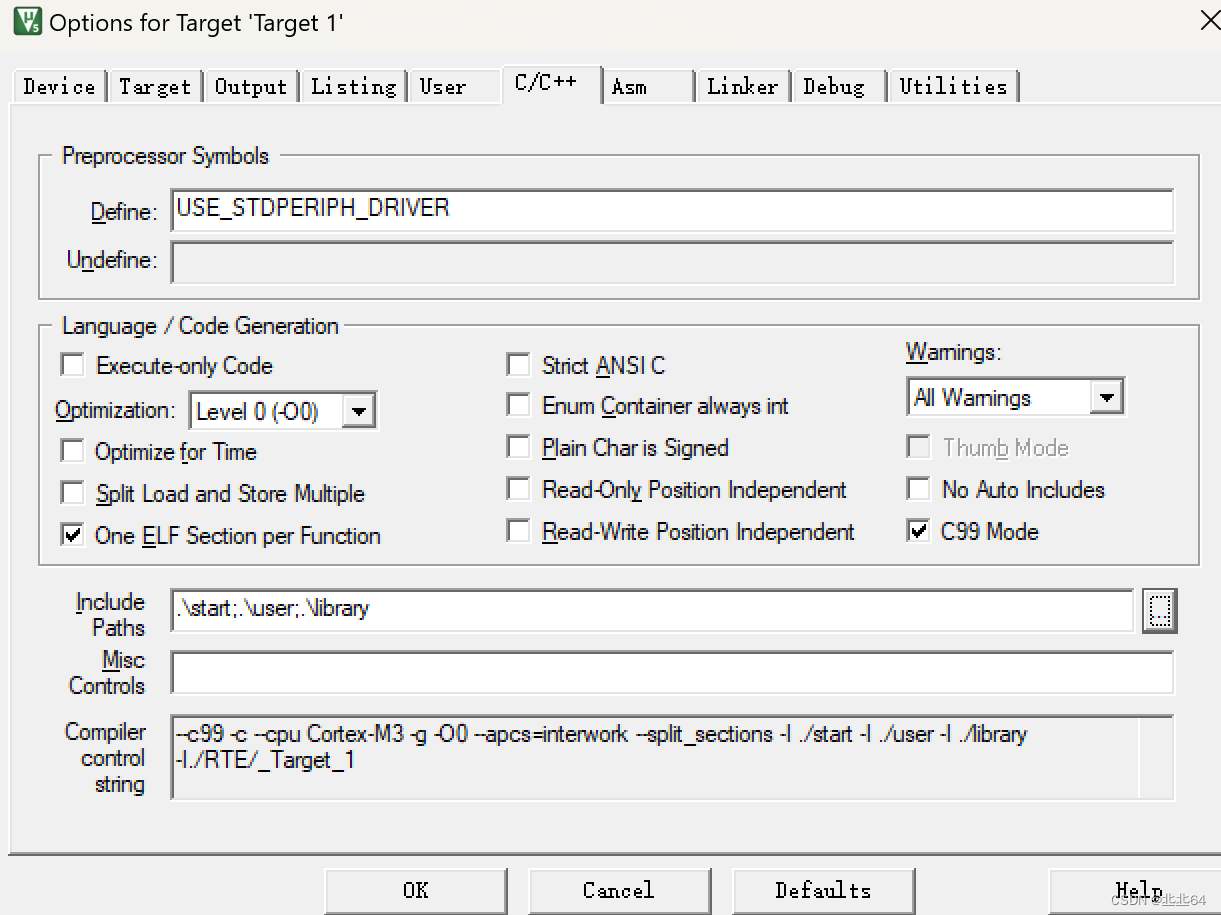
【STM32 |新建一个工程】基于标准库(库函数)新建工程
目录 STM32开发方式 库函数文件夹 建工程步骤 库函数工程建立 建立工程总结 STM32开发方式 目前stm32的开发方式主要有基于寄存器的方式、基于标准库的方式(库函数的方式)、基于HAL库的方式基于库函数的方式是使用ST官方提供的封装好的函数&…...

C#利用ClearScript执行Javascript脚本
1,新建.netframework winform工程 2,打开nuget程序包管理界面,安装Microsoft.ClearScript.V8,Microsoft.ClearScript.V8.Native.win-x64. 3,编写Javascript脚本,另存为demo.js function testFunc(t) {return t "…...

住宅ip与数据中心ip代理的区别是什么
代理通常意味着“替代”。它是用户设备和目标服务器之间的中介,允许在不同的IP地址下上网。代理ip根据来源分类可分住宅ip与数据中心ip,二者之间区别是什么呢? 住宅ip是由互联网服务提供商(ISP)提供给家庭的IP地址。出于这个原因,…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...