基于截断傅里叶级数展开的抖动波形生成
1、背景
抖动是影响信号完整性的重要因素。随着信号速率的不断提高,抖动的影响日益显著。仿真生成抖动时钟或抖动信号,对系统极限性能验证具有重要意义。抖动是定义在时域上的概念,它表征真实跳变位置(如跳边沿或过零点)与理想跳变位置之间的时间偏差。自然而然地,抖动信号生成也多从时域角度出发。考虑到时域和频域只是信号在不同维度上的表现方式。本文探索一种从频域角度生成抖动信号的方法,首先对方法的原理进行详细说明,然后比较与现有方法的优缺点,最后给出仿真验证结果。
2、原理
(1) 抖动时钟生成原理
周期信号可进行傅里叶级数展开,设周期信号 f ( t ) f(t) f(t)的周期为 T T T,则其三角函数的傅里叶级数展开表达式为
f ( t ) = A 0 + ∑ n = 1 ∞ [ A n c o s ( ω n t ) + B n s i n ( ω n t ) ] (1) f(t)=A_0+\sum_{n=1}^{\infty}[A_n cos(\omega_n t)+B_n sin(\omega_nt)]\tag{1} f(t)=A0+n=1∑∞[Ancos(ωnt)+Bnsin(ωnt)](1)
其中, ω n = n 2 π T \omega_n=n\frac{2\pi}{T} ωn=nT2π表示第 n n n个分量的角频率。 A 0 A_0 A0、 A n A_n An、 B n B_n Bn分别表示直流分量,余弦分量的幅度和正弦分量的幅度,它们的表达式分别为:
A 0 = 1 T ∫ t 0 t 0 + T f ( t ) d t A n = 2 T ∫ t 0 t 0 + T f ( t ) c o s ( ω n t ) d t B n = 2 T ∫ t 0 t 0 + T f ( t ) s i n ( ω n t ) d t A_0=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)dt \\A_n=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)cos(\omega_n t)dt\\B_n=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)sin(\omega_n t)dt A0=T1∫t0t0+Tf(t)dtAn=T2∫t0t0+Tf(t)cos(ωnt)dtBn=T2∫t0t0+Tf(t)sin(ωnt)dt
时钟信号是一种周期信号,为了将时钟信号表示为傅里叶级数展开的形式,需表示出时钟信号在一个周期内的表达式。

上图建立直角坐标系,对理想时钟信号进行表示,其中 T T T表示信号周期, τ r \tau_r τr和 τ f \tau_f τf分别表示上升时间和下降时间。 L = ( T − τ r − τ f ) / 2 L=(T-\tau_r-\tau_f)/2 L=(T−τr−τf)/2表示理想情况下平稳电平的时长。上图中未体现抖动的影响,抖动表现为实际跳变沿位置相对于跳边沿理想位置的时间偏差,带抖动的时钟信号示意图如下。

上图中蓝色虚线为理想跳边沿, t r t_r tr和 t f t_f tf分别表示上升沿和下降沿抖动值。图中标记了4个信号的关键转折点,分别记为 a a a、 b b b、 c c c、 d d d。这4个点的位置可分别表示为:
a = − L / 2 − τ r − t r = − 1 4 T − 3 4 τ r + 1 4 τ f − t r b = − L / 2 − t r = − 1 4 T + 1 4 τ r + 1 4 τ f − t r c = L / 2 − t f = 1 4 T − 1 4 τ r − 1 4 τ f − t f d = L / 2 + τ f − t f = 1 4 T − 1 4 τ r + 3 4 τ f − t f a=-L/2-\tau_r-t_r=-\frac{1}{4}T-\frac{3}{4}\tau_r+\frac{1}{4}\tau_f-t_r\\b=-L/2-t_r=-\frac{1}{4}T+\frac{1}{4}\tau_r+\frac{1}{4}\tau_f-t_r\\c=L/2-t_f=\frac{1}{4}T-\frac{1}{4}\tau_r-\frac{1}{4}\tau_f-t_f\\d=L/2+\tau_f-t_f=\frac{1}{4}T-\frac{1}{4}\tau_r+\frac{3}{4}\tau_f-t_f a=−L/2−τr−tr=−41T−43τr+41τf−trb=−L/2−tr=−41T+41τr+41τf−trc=L/2−tf=41T−41τr−41τf−tfd=L/2+τf−tf=41T−41τr+43τf−tf
由此,带抖动的时钟信号的表达式为:
f ( t ) = { 0 , − T 2 ≤ t < a v b − a ( t − a ) , a < t ≤ b v , b < t ≤ c v c − d ( t − d ) , c < t ≤ d 0 , d < t ≤ T / 2 f(t)= \left\{\begin{matrix} 0,-\frac{T}{2}\leq t<a \\ \frac{v}{b-a}(t-a),a<t\leq b \\ v, b<t\leq c \\ \frac{v}{c-d}(t-d),c<t\leq d\\ 0, d<t\leq T/2 \end{matrix}\right. f(t)=⎩ ⎨ ⎧0,−2T≤t<ab−av(t−a),a<t≤bv,b<t≤cc−dv(t−d),c<t≤d0,d<t≤T/2
将 f ( t ) f(t) f(t)的表达式带入 A 0 A_0 A0、 A n A_n An、 B n B_n Bn的表达式中,可求得:
A 0 = 1 T ∫ t 0 t 0 + T f ( t ) d t = 1 T ∫ − T / 2 T / 2 f ( t ) d t = 1 T [ ∫ a b v b − a ( t − a ) d t + ∫ b c v d t + ∫ c d v c − d ( t − d ) d t ] = 1 T [ 1 2 v ( b − a ) + 1 2 v ( c + b ) ( c − b ) + 1 2 v ( d − c ) ] = v 2 T [ ( b − a ) + ( c + b ) ( c − b ) + ( d − c ) ] (2) A_0=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)dt=\frac{1}{T}\int_{-T/2}^{T/2}f(t)dt\\=\frac{1}{T}[\int_{a}^{b}\frac{v}{b-a}(t-a)dt+\int_{b}^{c}vdt+\int_{c}^{d}\frac{v}{c-d}(t-d)dt]\\=\frac{1}{T}[\frac{1}{2}v(b-a)+\frac{1}{2}v(c+b)(c-b)+\frac{1}{2}v(d-c)]\\=\frac{v}{2T}[(b-a)+(c+b)(c-b)+(d-c)]\tag{2} A0=T1∫t0t0+Tf(t)dt=T1∫−T/2T/2f(t)dt=T1[∫abb−av(t−a)dt+∫bcvdt+∫cdc−dv(t−d)dt]=T1[21v(b−a)+21v(c+b)(c−b)+21v(d−c)]=2Tv[(b−a)+(c+b)(c−b)+(d−c)](2)
A n = 2 T ∫ − T / 2 T / 2 f ( t ) c o s ( ω n t ) d t = 2 T [ ∫ a b v ( t − a ) b − a c o s ( ω n t ) d t + ∫ b c v c o s ( ω n t ) d t + ∫ c d v ( t − d ) c − d c o s ( ω n t ) d t ] = 2 T [ v ( c o s ( ω n b ) − c o s ( ω n a ) ) ( b − a ) ω n 2 + v ( c o s ( ω n d ) − c o s ( ω n c ) ) ( c − d ) ω n 2 + v ( s i n ( ω n c ) − s i n ( ω n b ) ) ω n ] (3) A_n=\frac{2}{T}\int_{-T/2}^{T/2}f(t)cos(\omega_n t)dt\\=\frac{2}{T}[\int_{a}^{b}\frac{v(t-a)}{b-a}cos(\omega_n t)dt+\int_{b}^{c}vcos(\omega_n t)dt+\int_{c}^{d}\frac{v(t-d)}{c-d}cos(\omega_n t)dt]\\=\frac{2}{T}[\frac{v(cos(\omega_n b)-cos(\omega_n a))}{(b-a)\omega_n^2}+\frac{v(cos(\omega_n d)-cos(\omega_n c))}{(c-d)\omega_n^2}+\frac{v(sin(\omega_n c)-sin(\omega_n b))}{\omega_n}] \tag{3} An=T2∫−T/2T/2f(t)cos(ωnt)dt=T2[∫abb−av(t−a)cos(ωnt)dt+∫bcvcos(ωnt)dt+∫cdc−dv(t−d)cos(ωnt)dt]=T2[(b−a)ωn2v(cos(ωnb)−cos(ωna))+(c−d)ωn2v(cos(ωnd)−cos(ωnc))+ωnv(sin(ωnc)−sin(ωnb))](3)
B n = 2 T ∫ − T / 2 T / 2 f ( t ) s i n ( ω n t ) d t = 2 T [ ∫ a b v ( t − a ) b − a s i n ( ω n t ) d t + ∫ b c v s i n ( ω n t ) d t + ∫ c d v ( t − d ) c − d s i n ( ω n t ) d t ] = 2 T [ v ( s i n ( ω n b ) − s i n ( ω n a ) ) ( b − a ) ω n 2 + v ( s i n ( ω n d ) − s i n ( ω n c ) ) ( c − d ) ω n 2 + v ( c o s ( ω n b ) − c o s ( ω n c ) ) ω n ] (4) B_n=\frac{2}{T}\int_{-T/2}^{T/2}f(t)sin(\omega_n t)dt\\=\frac{2}{T}[\int_{a}^{b}\frac{v(t-a)}{b-a}sin(\omega_n t)dt+\int_{b}^{c}vsin(\omega_n t)dt+\int_{c}^{d}\frac{v(t-d)}{c-d}sin(\omega_n t)dt]\\=\frac{2}{T}[\frac{v(sin(\omega_n b)-sin(\omega_n a))}{(b-a)\omega_n^2}+\frac{v(sin(\omega_n d)-sin(\omega_nc))}{(c-d)\omega_n^2}+\frac{v(cos(\omega_n b)-cos(\omega_n c))}{\omega_n}] \tag{4} Bn=T2∫−T/2T/2f(t)sin(ωnt)dt=T2[∫abb−av(t−a)sin(ωnt)dt+∫bcvsin(ωnt)dt+∫cdc−dv(t−d)sin(ωnt)dt]=T2[(b−a)ωn2v(sin(ωnb)−sin(ωna))+(c−d)ωn2v(sin(ωnd)−sin(ωnc))+ωnv(cos(ωnb)−cos(ωnc))](4)
显然,在已知上述傅里也变换级数的各项系数时,即可将原始时域周期信号用傅里叶级数表示出来,需要注意的是,在实际运算时,谐波索引 n n n不能取到无穷大。所以,实际只能得到信号的截断傅里叶级数展开的形式,保留的谐波次数越高,得到的波形越准确,但计算量越大。
需要注意的是,利用(1)式将原始信号表示为傅里叶级数展开的形式时 t t t被限制在了 [ − T / 2 , T / 2 ] [-T/2,T/2] [−T/2,T/2]的范围内,所以只生成了一个周期的信号。为了生成多个周期的信号,我们需要按照上面的方式,生成多个周期的信号,并将各个周期的信号拼接成完整的信号,其中各个周期的上升/下降时间及抖动值都是可以独立指定的。
此外,上面生成时,考虑时钟低电平为0,可根据实际要求,对波形进行上下平移,以调整波形的offset。
(2) 抖动信号生成原理
本文以NRZ和PAM4信号为例,说明抖动信号的生成原理。NRZ和PAM4信号与时钟信号的不同在于NRZ/PAM4并非周期信号,所以相比于时钟信号,带抖动的NRZ/PAM4信号虽然能借鉴抖动时钟信号的生成方法,但需进行一定的修改和适配。具体地,如下图所示相邻两个NRZ符号有4种可能状态,分别为’00’,‘01’,‘10’和’11’;相邻两个PAM4符号有16种可能状态,分别为’00’, ‘01’, ‘02’, ‘03’, ‘10’, ‘11’, ‘12’, ‘13’, ‘20’, ‘21’ ,‘22’, ‘23’, ‘30’, ‘31’, ‘32’, ‘33’。所以,可以将NRZ和PAM4的符号两两组合,进行波形生成,其中除非跳变位置的波形,如’00’,‘11’,‘22’,'33’外,其他跳变波形均能参照抖动时钟的生成方法,只需对波形表达式进行略有的适配即可。


未完待续。。。
未完待续。。。
未完待续。。。
未完待续。。。
相关文章:

基于截断傅里叶级数展开的抖动波形生成
1、背景 抖动是影响信号完整性的重要因素。随着信号速率的不断提高,抖动的影响日益显著。仿真生成抖动时钟或抖动信号,对系统极限性能验证具有重要意义。抖动是定义在时域上的概念,它表征真实跳变位置(如跳边沿或过零点)与理想跳变位…...
——支持撤销的画线行为)
图片标注编辑平台搭建系列教程(9)——支持撤销的画线行为
文章目录 背景渲染行为mouseDownmouseMovemouseDbclick总结背景 编辑器中的绘制,要想做的足够好,是需要支持撤销形点的,因为作业员在绘制过程中,可能会点错位置,需要及时撤销,否则影响编辑效率。撤销我们知道,需要通过ID编辑器的history的undo来实现,那么意味着,每一…...
)
赶紧收藏!2024 年最常见 100道 Java 基础面试题(四十一)
上一篇地址:赶紧收藏!2024 年最常见 100道 Java 基础面试题(四十)-CSDN博客 八十一、tcp为什么要三次握手,两次不行吗?为什么? TCP(传输控制协议)使用三次握手…...

使用自关联方法处理多表关系
使用自关联方法处理多表关系 这里通过省市区之间的关系来解释自关联的情况 在设置地址的过程中 , 不可避免的需要设置 , 省份 ,市以及区 而省市区三者之间的具有一定的关联关系 一个省份对应多个市 一个市对应多个区 如果通过设置主表从表关系则需要设置三张标分别对应省…...

annaconda详细解读换源文件
annaconda换源详细解读文件 annaconda换源详细解读文件 annaconda换源详细解读文件 #踩坑/annaconda换源详细解读通道问题 如何准确使用国内源高效安装GPU版本的Pytorch - 知乎 文件中的custom通道,需要自己手动添加到默认通道里面,记得后面更上/包名…...
的实践技巧)
AI大模型系列:编写高质量提示(prompt)的实践技巧
AI大模型系列专栏 文章收录于AI大模型系列专栏 文明基石,文字与数字的起源与演变自然语言处理,从规则到统计的演变AI魔法师,提示工程的力量编写高质量提示(prompt)的小技巧编写高质量提示(prompt…...
汽车EDI:安通林Antolin EDI 项目案例
安通林(Antolin)是一家全球性的汽车零部件制造商,专注于汽车内饰系统和零部件的生产,致力于创新和采用先进的技术。近年来 安通林Antolin 推动其供应商部署EDI系统,使得双方能够通过EDI传输业务单据,极大提…...

今日arXiv最热NLP大模型论文:揭露大语言模型短板,北京大学提出事件推理测试基准
人工智能领域又一里程碑时刻!北京大学、北京智源人工智能研究院等机构联合推出大型事件推理评测基准 。这是首个同时在知识和推理层面全面评估大模型事件推理能力的数据集。 总所周知,事件推理需要丰富的事件知识和强大的推理能力,涉及多种推…...
windows系统安装Ubuntu子系统
安装前先在 控制面板 中打开 程序与功能选项 ,点击 启用或关闭Windows功能: 勾选 适用于 Linux的Windows子系统 和 虚拟机平台 、 Hyper-v 。 重启电脑后再 Microsoft Store Windows应用商店 中下载合适的Ubuntu版本。 运行Ubuntu程序,如出现…...

电脑复制和粘贴的时候会出现Hello!
电脑不管是Microsoft Excel还是Microsoft Word复制之后粘贴过来就出现HELLO,当复制粘贴文件的时候就会出现WINFILE; 具体现象看下面两个图片: 这是因为winfile 文件病毒(幽灵蠕虫病毒),每月的28号发作; 症状…...

AI新视界:探索Baidu Comate的前沿科技
前言 Baidu Comate(智能代码助手)是基于文心大模型,结合百度积累多年的编程现场大数据和外部优秀开源数据,打造的新一代编码辅助工具。拥有代码智能、场景丰富、创造价值、广泛应用等多重产品优势,可实现“帮你想、帮…...

唐山知识付费系统搭建教程,女性创业难吗?2017十佳女性创业故事:黑科技创业“女神”
女性创业难吗?2017十佳女性创业故事:黑科技创业“女神”!创业似乎一直是一个比较热门的话题,女性创业也是一个很有争议的问题。女性创业难吗?看看2017十佳女性创业故事:黑科技创业“女神”。 阿里研究院、中国企业家木兰汇、阿里巴巴创新中…...

Hotcoin Research | 模块化将是大势所趋:拆解模块化区块链的现状和未来
关于模块化区块链叙事的讨论源于Celestia和其代币TIA的亮眼表现。实际上,模块化是未来区块链设计的主要发展方向和大势所趋。模块化区块链就像乐高积木一样,将区块链系统拆分为可重用的模块,通过定制组合可实现不同功能的区块链网络。这种灵活…...
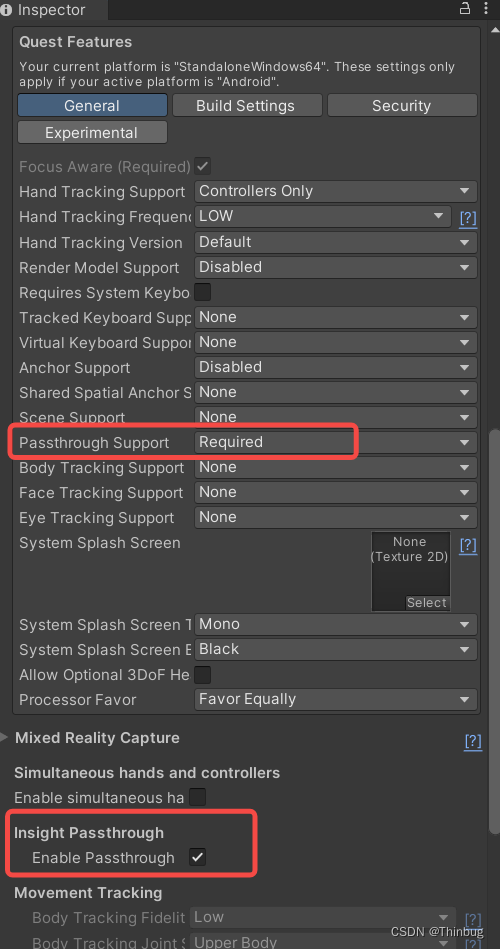
Unity VR在编辑器下开启Quest3透视(PassThrough)功能
现在有个需求是PC端串流在某些特定时候需要开启透视。我研究了两天发现一些坑,记录一下方便查阅,也给没踩坑的朋友一些思路方案。 先说结论,如果要打PC端或者在Unity编辑器中开启,那么OpenXR当前是不行的可能还需要一个长期的过程,必须需要切换到Oculus。当然Unity官方指…...

使用 git rebase 还是 git merge,优缺点
在开发过程中使用 git rebase 还是 git merge,优缺点分别是什么? - 知乎 看一下gerrit的模式 永远rebase 绝对禁用merge 每一个commit都是一个完整的功能 保持清晰直观的提交历史 所以,main 分支是万万不能使用 rebase 的!&#…...

李飞飞团队 AI4S 最新洞察:16 项创新技术汇总,覆盖生物/材料/医疗/问诊……
不久前,斯坦福大学 Human-Center Artificial Intelligence (HAI) 研究中心重磅发布了《2024年人工智能指数报告》。 作为斯坦福 HAI 的第七部力作,这份报告长达 502 页,全面追踪了 2023 年全球人工智能的发展趋势。相比往年,扩大了…...
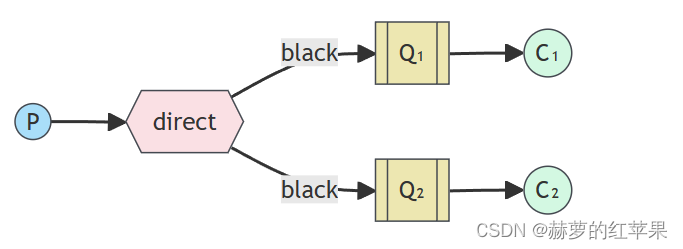
springboot整合rabbitmq的不同工作模式理解
前提是已经安装并启动了rabbitmq,并且项目已经引入rabbitmq,完成了配置。 不同模式所需参数不同,生产者可以根据参数不同使用重载的convertAndSend方法。而消费者均是直接监听某个队列。 不同的交换机是实现不同工作模式的关键组件.每种交换…...

Ansible(二)
一、Playbook基础 1.1 Playbook定义 Playbook其实是Ansible服务的一个配置文件,Ansible使用Playbook的YAML语言配置编写成操作需求,实现对远端主机或策略部署,实现对远端主机的控制与管理。 1.2 Playbook组成 Tasks:任务&…...
【linux】linux工具使用
这一章完全可以和前两篇文件归类在一起,可以选择放一起看哦 http://t.csdnimg.cn/aNaAg http://t.csdnimg.cn/gkJx7 拖更好久了,抱歉,让我偷了会懒 1. 自动化构建工具 make , makefile make 是一个命令,makefile 是一个文件&…...
Docker需要代理下载镜像
systemctl status docker查看docker的状态和配置文件是/usr/lib/systemd/system/docker.service vi /usr/lib/systemd/system/docker.service, 增加如下配置项 [Service] Environment"HTTP_PROXYhttp://proxy.example.com:8080" "HTTPS_PROXYhttp:…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
