electron 多窗口 vuex/pinia 数据状态同步简易方案(利用 LocalStorage)
全局 stroe 添加 mutations 状态同步方法
// 用于其他窗口同步 vuex 中的 DeviceTcpDataasyncDeviceTcpData(state: StateType, data: any) {state.deviceTcpData = data},
App.vue 里
onMounted(() => {console.log("App mounted");/*** vuex 多窗口 store 同步*/// 1. 初始赋值// 从 localStorage 同步 tcp 上报的数据到 vuexconst deviceTcpData = localStorage.getItem("deviceTcpData");if (deviceTcpData) {store.commit("asyncDeviceTcpData", JSON.parse(deviceTcpData));}// 2. 监听 storage 事件 同步 全局 state// 其他渲染进程,当设置进程进行修改storage的时候,其他进程可以根据storage变化来更改自己的storewindow.addEventListener("storage", () => {const deviceTcpData = localStorage.getItem("deviceTcpData");deviceTcpData &&store.commit("asyncDeviceTcpData", JSON.parse(deviceTcpData));});// 从主界面关闭时,清空本地存储的数据 (清除 localstorage 的时机)window.addEventListener("beforeunload", (e: any) => {if (route.name === "search") {localStorage.removeItem("deviceTcpData");}});
});
关键: 利用 watch 监听全局 state 的变动,每次变动,进行 localStorage 同步
// 监听 全局 store 的变动
watch(() => store.state.deviceTcpData,(val) => {console.log("watch 触发");console.log(val);localStorage.setItem("deviceTcpData", JSON.stringify(val));},{deep: true,}
);
缺点: 数据量大时,消耗性能较高。可用作少量数据的同步方案;
相关文章:
)
electron 多窗口 vuex/pinia 数据状态同步简易方案(利用 LocalStorage)
全局 stroe 添加 mutations 状态同步方法 // 用于其他窗口同步 vuex 中的 DeviceTcpDataasyncDeviceTcpData(state: StateType, data: any) {state.deviceTcpData data},App.vue 里 onMounted(() > {console.log("App mounted");/*** vuex 多窗口 store 同步*//…...

自定义数据集图像分类实现
模型训练 要使用自己的图片分类数据集进行训练,这意味着数据集应该包含一个目录,其中每个子目录代表一个类别,子目录中包含该类别的所有图片。以下是一个使用Keras和TensorFlow加载自定义图片数据集进行分类训练的例子。 我们自己创建的数据集…...

【C++】手搓读写ini文件源码
【C】手搓读写ini文件源码 思路需求:ini.hini.cppconfig.confmian.cpp 思路 ini文件是一种系统配置文件,它有特定的格式组成。通常做法,我们读取ini文件并按照ini格式进行解析即可。在c语言中,提供了模板类的功能,所以…...

undolog
undolog回滚段 undolog执行的时间:在执行器操作bufferpool之前。 undolog页...

项目文档分享
Hello , 我是小恒。提前祝福妈妈母亲节快乐 。 本文写一篇初成的项目文档 (不是README.md哈),仅供参考 项目名称 脚本存储网页 项目简介 本项目旨在创建一个网页,用于存储和展示各种命令,用户可以通过粘贴复制命令到…...
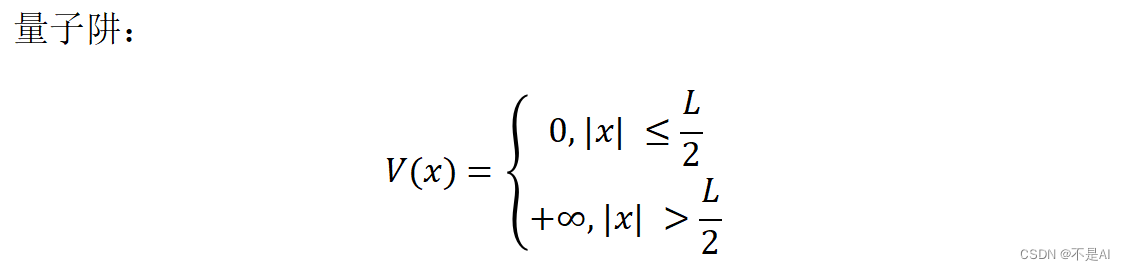
【深耕 Python】Quantum Computing 量子计算机(5)量子物理概念(二)
写在前面 往期量子计算机博客: 【深耕 Python】Quantum Computing 量子计算机(1)图像绘制基础 【深耕 Python】Quantum Computing 量子计算机(2)绘制电子运动平面波 【深耕 Python】Quantum Computing 量子计算机&…...

手写Spring5【笔记】
Spring5【笔记】 前言前言推荐Spring5【笔记】1介绍2手写 最后 前言 这是陈旧已久的草稿2022-12-01 23:32:59 这个是刷B站的时候,看到一个手写Spring的课程。 最后我自己好像运行不了,就没写。 现在2024-5-12 22:22:46,发布到[笔记]专栏中…...

2024中国(重庆)机器人展览会8月举办
2024中国(重庆)机器人展览会8月举办 邀请函 主办单位: 中国航空学会 重庆市南岸区人民政府 招商执行单位: 重庆港华展览有限公司 2024中国重庆机器人展会将汇聚机器人全产业链知名企业,世界科技领先的生产制造企业与来自多个国家和地区…...
)
Apache 开源项目文档中心 (英文 + 中文)
进度:持续更新中。。。 Apache Ambari 2.7.5 Apache Ambari Installation 2.7.5.0 (latest)Apache Ambari Installation 2.7.5.0 中文版 (latest) Apache DolphinScheduler Apache DolphinScheduler 1.2.0 中文版Apache DolphinScheduler 1.2.1 中文版...

蓝桥杯 算法提高 ADV-1164 和谐宿舍 python AC
贪心,二分 同类型题:蓝桥杯 算法提高 ADV-1175 打包 def judge(x):wood 0max_val 0ans_len 0for i in ll:if i > x:return Falseelif max(max_val, i) * (ans_len 1) < x:max_val max(max_val, i)ans_len 1else:wood 1max_val ians_len …...
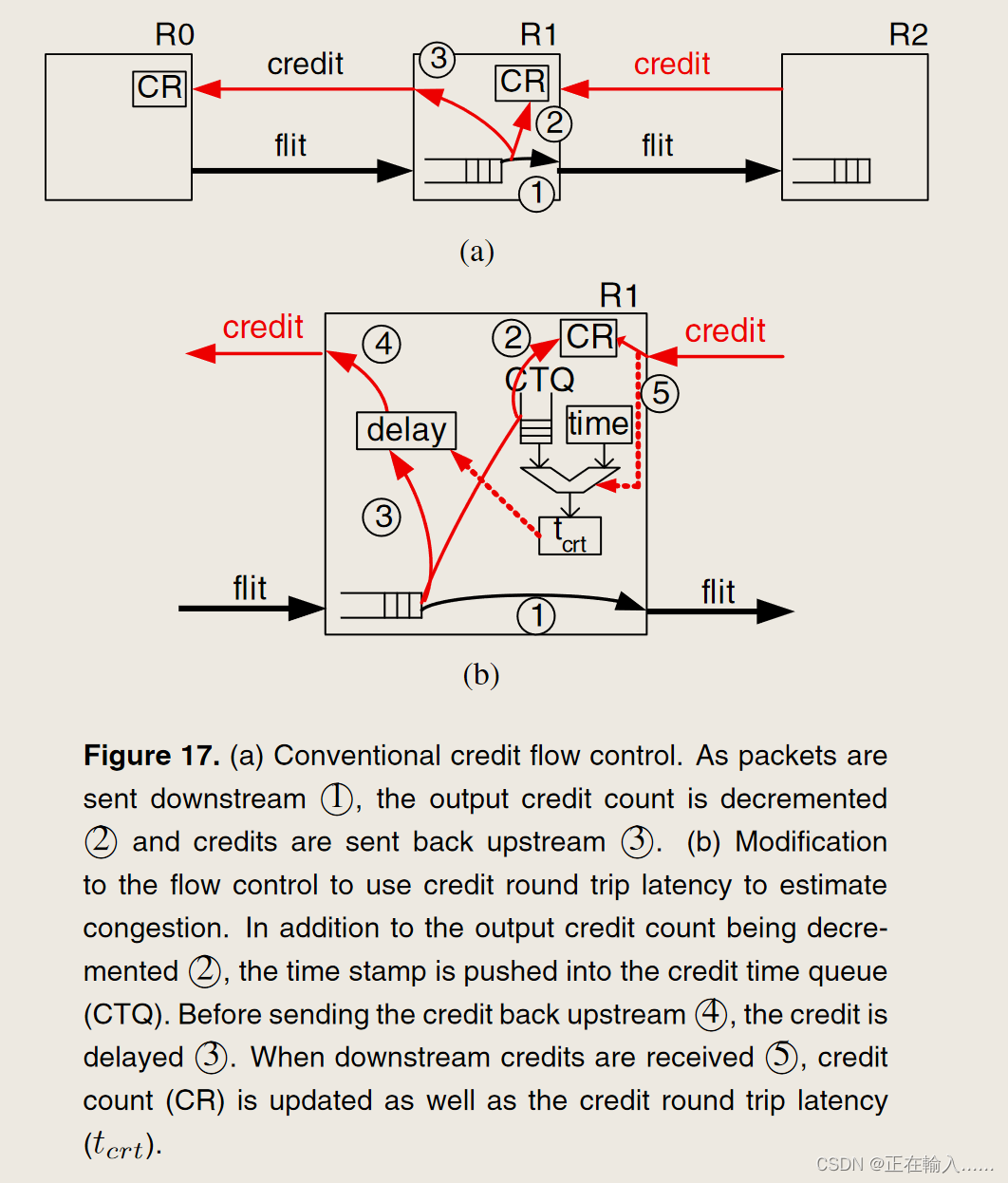
Dragonfly 拓扑的路由算法
Dragonfly 拓扑的路由算法 1. Dragonfly 上的路由 (1)最小路由(2)非最小路由 2. 评估3. 存在问题 (1)吞吐量限制(2)较高的中间延迟 references Dragonfly 拓扑的路由算法 John Kim, William J. Dally 等人在 2008 年的 ISCA 中提出技术驱动、高度可扩展的 Dragonfly 拓扑。而…...

android基础-服务
同样使用intent来传递服务 oncreate是服务第一次启动调用,onStartCommand是服务每次启动的时候调用,也就是说服务只要启动后就不会调用oncreate方法了。可以在myservice中的任何位置调用stopself方法让服务停止下来。 服务生命周期 前台服务类似于通知会…...

mysql 事物
MySQL中的事务(Transaction)是一个确保数据完整性和一致性的重要概念。它将一组SQL操作捆绑在一起,当作一个单一的工作单元来执行。事务具备以下四个关键特性,即ACID特性: 原子性(Atomicity)&am…...

Unity Shader中获取像素点深度信息
1.顶点着色器中对深度进行计算 v2f vert(appdata v) {v2f o;o.pos UnityObjectToClipPos(v.vertex);o.uv TRANSFORM_TEX(v.uv, _MainTex);o.depth (o.pos.z / o.pos.w 1.0) * 0.5; // Normalize depth to [0, 1]return o; }但是达不到预期,最后返回的值一直大于…...

ROS——Action学习
文章目录 ROS Action概念自定义Action类型参考ROS Action概念 ROS Service会阻塞程序流,程序无法进行其它的工作,有时我们需要同时进行多个任务。 ROS Action可以满足要求,ROS Action提供程序的非阻塞执行。 Action是ROS Node的通信方式之一 Action server 向ROS系统广…...
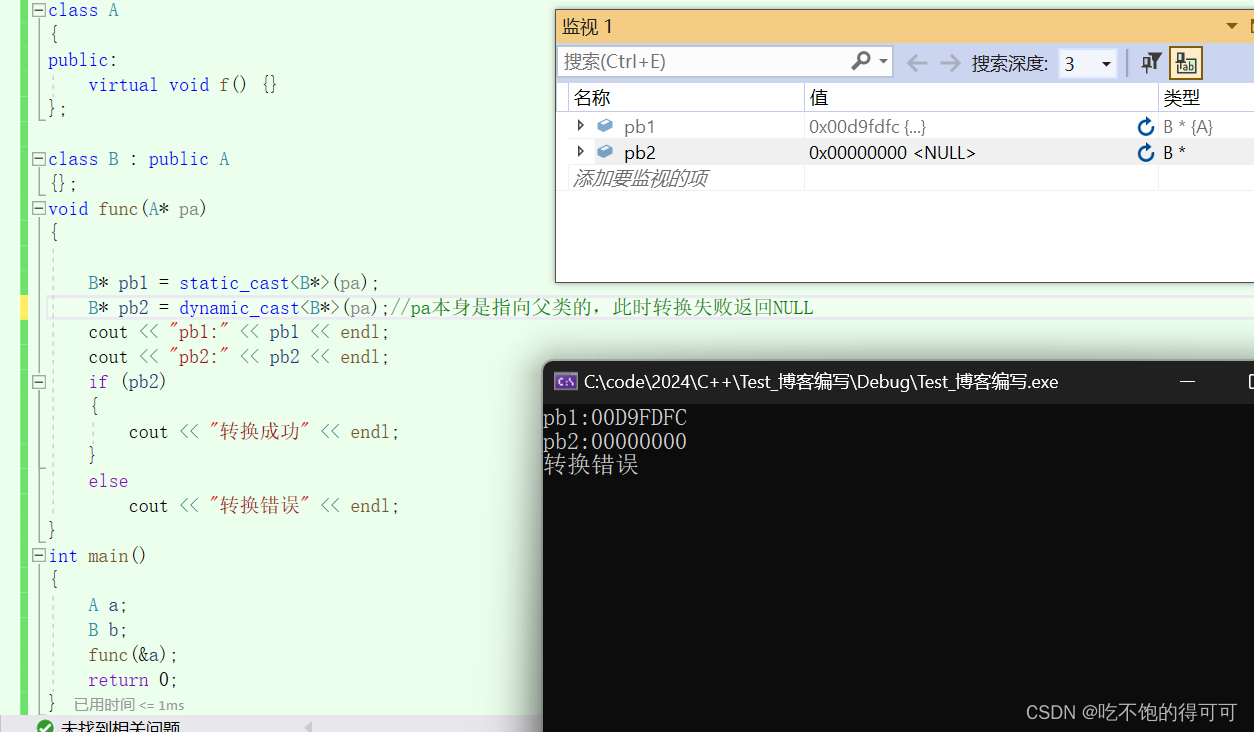
基于C语言中的类型转换,C++标准创造出了更加可视化的类型转换
目录 前言 一、 C语言中的类型转换 二、为什么C需要四种类型转换 三、C中新增的四种强制类型转换操作符以及它们的应用场景 1.static_cast 2.reinterpret_cast 3.const_cast 4.dynamic_cast 前言 在C语言中,如果赋值运算符左右两侧的类型不同,或者…...

如何创建族表
https://jingyan.baidu.com/article/c275f6bafa5714a23c756768.html...

【UnityRPG游戏制作】Unity_RPG项目_PureMVC框架应用
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:就业…...

并行计算的一些知识点分享--并行系统,并行程序, 并发,并行,分布式
并行计算 核是个啥? 在并行计算中,“核”通常指的是处理器的核心(CPU核心)。每个核心都是一个独立的处理单元,能够执行计算任务。多核处理器指的是拥有多个这样核心的单一物理处理器,这样的设计可以允许多…...

设计模式:访问者模式
访问者模式(Visitor Pattern)是行为设计模式的一种,它使你能够在不修改对象结构的情况下,给对象结构中的每个元素添加新的功能。访问者模式将数据结构和作用于结构上的操作解耦,使得操作集合可相对自由地演化。 核心概…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
