Golang编译优化——稀疏条件常量传播
文章目录
- 一、概述
- 二、稀疏条件常量传播
- 2.1 初始化worklist
- 2.2 构建def-use链
- 2.3 更新值的lattice
- 2.4 传播constant值
- 2.5 替换no-constant值
一、概述
常量传播(constant propagation)是一种转换,对于给定的关于某个变量 x x x和一个常量 c c c的赋值 x ← c x\leftarrow c x←c,这种转换用 c c c来替代以后出现的 x x x的引用,只要在这期间没有出现另外改变 x x x值的赋值。
如下图a的CFG所示,基本块B1中的指令 b ← 3 b\leftarrow 3 b←3将常量3赋给 b b b,并且CFG中没有其他对 b b b的赋值。图b是对图a做常量传播的结果,此时 b b b的所有出现都已被3替换,但都没有对结果得到的常数表达式进行计算(就是常量折叠,这里也可以直接结算)。
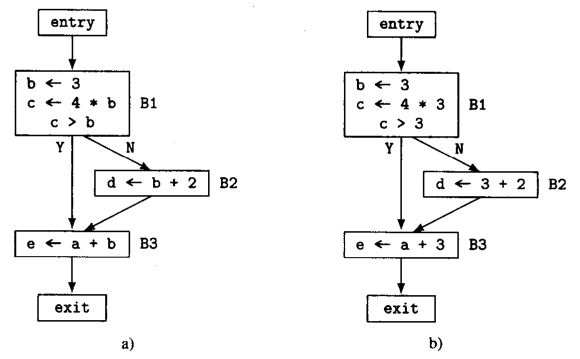
正是因为常量传播的优化操作,使得指令 b ← 3 b\leftarrow 3 b←3成为无用代码(没有在其他的指令操作数中引用),死代码删除时可以将 b ← 3 b\leftarrow 3 b←3删除。
在《编译器设计》总结中介绍过稀疏简单常量传播(Sparse Simple Constant Propagation,SSCP),如果常量传播掌握的不多建议仔细阅读,重点要明白半格(semilattice)。
这里将要介绍的是稀疏条件常量传播(Sparse Conditional Constant Propagation,SCCP),它和SSCP实现方法相似,只是传播方式不同,两者在CFG中处理常量传播时的主要区别如下:
- 传播方式。SCCP的常量值只沿着可达的控制流路径传播,当遇到条件分支时,只有符合条件的路径上的常量值才会被传播;SSCP则是一种更为简单的常量传播方法,它不考虑控制流条件,而是在整个控制流图中的所有路径上进行常量传播。
- 传播精度。SCCP由于只在符合条件的控制流路径上传播常量,因此稀疏条件常量传播的精度相对较高。它能够更准确地确定哪些值可以在运行时被计算为常量。SSCP稀疏简单常量传播的精度相对较低,因为它忽略了条件分支,常常会导致在一些路径上的常量传播不正确。
- 复杂度。SCCP由于考虑了控制流条件,稀疏条件常量传播的算法复杂度相对较高,但它更准确。SSCP稀疏简单常量传播的算法相对简单,但它的精度较低,可能会导致一些常量传播的机会被忽略。
二、稀疏条件常量传播
Golang中关于SCCP的实现在文件src/cmd/compile/internal/ssa/sccp.go中,算法的开始函数是sccp(f *Func) 函数。SCCP算法实现的步骤主要分为:
- 初始化
worklist: 首先,需要初始化worklist中存放的必要数据结构,以便记录控制流图、变量的使用情况和 lattice 等信息。 - 构建
def-use链: 遍历函数的基本块和值,构建每个值的def-use链,以确定哪些值的常量可以被传播。 - 更新值的
lattice: 遍历每个基本块和其中的值,对每个值应用稀疏条件常量传播算法。这包括检查值的操作类型,确定其是否可以被折叠为常量,并根据其值更新lattice。 - 传播常量值: 通过控制流图传播常量值。对于具有多个后继的基本块,根据条件值的
lattice更新传播路径。 - 替换非常量值: 一旦确定了可以替换为常量的值,将其替换为相应的常量。同时,更新相应基本块的控制流以反映这些常量值的传播。
以下是我提取的 SSA IR 代码片段。接下来,将详细介绍 SCCP 算法的实现步骤,并在解释过程中引入这段代码,以帮助理解。
b1:v1 = InitMem <mem>v5 = Const64 <int> [0]v6 = Const64 <int> [1]v7 = Const64 <int> [2]v8 = Const64 <int> [3]v9 = Add64 <int> v8 v7v10 = Less64 <bool> v5 v6
If v10 → b3 b2b3: ← b1v13 = Add64 <int> v6 v7
Plain → b2b2: ← b1 b3v19 = Phi <int> v9 v13v16 = Add64 <int> v6 v7v18 = Add64 <int> v7 v8v20 = Add64 <int> v19 v16v21 = Add64 <int> v20 v18v23 = MakeResult <int,mem> v21 v1
Ret v23
2.1 初始化worklist
worklist是一个存放多种数据结构的集合,也可以认为是SCCP算法的上下文,其结构定义如下:
type worklist struct {f *Func // 当前正在优化的函数edges []Edge // 传播时遍历CFG的edge队列,广度优先遍历uses []*Value // 当一个值的lattice改变时,将其使用链append其中visited map[Edge]bool // 记录一条edge是否传播过latticeCells map[*Value]lattice // 值的lattice,传播过程会更新defUse map[*Value][]*Value // 非控制值的def-use链defBlock map[*Value][]*Block // 控制值的def-use链,控制值只在个别块中使用visitedBlock []bool // 记录一个block是否访问过
}
初始化worklist就是初始化worklist中的数据结构,如上代码块。需要注意defUse和defBlock,其map的key是Value对象,map的value是个一维数组。
2.2 构建def-use链
def-use链是指Value的定义和使用之间的关系链,对任意一个Value的定义,都可以通过def-use链找到所有使用该Value的目标(以该Value为参数的Value)。如IR片段中的定义v6,使用过v6的Value有v10,v13和v16,所以defUse[v6] = {v10, v13, v16}。控制Value的定义,对应的使用都是Block。如IR片段中的定义v10,使用v10的Block有If,所以defBlock[v10] = {If}
这里不需要为所有的Value构建def-use链,而只为可能为常量(lattice为top或constant) 的Value构建。因为对于不可能是常量(lattice为bottom) 的Value,不管其lattice更新多少次,都会保持bottom不变。构建规则如下:
- 如果一个Value
v1的定义可能为常量,且引用v1的Valuev2也可能为常量,则将v2加入到v1的def-use链defUse[v1]中; - 如果一个Value
v1的定义可能为常量,但引用v1的Valuev2不可能是常量,则不能将v2加入到v1的def-use链defUse[v1]中; - 如果一个Value
v1的定义不可能是常量,则不用构建v1的def-use链defUse[v1]。
检测一个Value是否可能为常量由possibleConst函数实现。如果一个Value的opcode是常量操作(ConstBool、ConstString、ConstNil、Const8等),那么该Value肯定就是一个常量。如果一个Value的opcode能够满足,一旦操作数是常量,其结果肯定就是常量,那么该Value可能就是一个常量。这类opcode有算数运算、位运算、比较、转换等。
构建def-use链的过程,在buildDefUses函数中实现。其主要逻辑如下:
- 遍历函数的Block。
- 遍历Block的Value的定义
val。
如果val与其参数arg满足上文构建规则1,则将val加入到arg对应的def-use链中,即t.defUse[arg] = append(t.defUse[arg], val)。 - 遍历Block的控制Value
ctl。
如果ctl可能是常量,则将当前块加入到ctl对应的def-use链中,即t.defBlock[ctl] = append(t.defBlock[ctl], block)。
- 遍历Block的Value的定义
构建IR片段def-use链,Value和控制Value分别得到的defUse和defBlock分别如下:
defUse = map[*Value][]*Value {//def usev5: {v10},v6: {v10,v13,v16},v7: {v9,v13,v16,v18},v8: {v9,v18},v9: {v19},v13: {v19},v19: {v20},v16: {v20},v18: {v21},v20: {v21},// v1不可能是常量
}defBlock = map[*Value][]*Block {//def usev10: {If},// v23不可能是常量
}
2.3 更新值的lattice
2.4 传播constant值
2.5 替换no-constant值
相关文章:

Golang编译优化——稀疏条件常量传播
文章目录 一、概述二、稀疏条件常量传播2.1 初始化worklist2.2 构建def-use链2.3 更新值的lattice2.4 传播constant值2.5 替换no-constant值 一、概述 常量传播(constant propagation)是一种转换,对于给定的关于某个变量 x x x和一个常量 c …...

人工智能培训讲师咨询叶梓介绍及智能医疗技术与ChatGPT临床应用三日深度培训提纲
1、授课老师简介 叶梓,上海交通大学计算机专业博士毕业,高级工程师。主研方向:数据挖掘、机器学习、人工智能。历任国内知名上市IT企业的AI技术总监、资深技术专家,市级行业大数据平台技术负责人。 长期负责城市信息化智能平台的…...
HCIP(BGP综合实验)--8
一:实验要求 二:实现过程 (一)配置IP地址: AR1: [AR1]int g0/0/0 [AR1-GigabitEthernet0/0/0]ip add 12.1.1.1 24 [AR1-GigabitEthernet0/0/0]int l0 [AR1-LoopBack0]ip add 172.16.0.1 32 [AR1-LoopBack0]int l1 […...

深入理解C++中的Vector容器:用容器构建高效程序
文章目录 vector介绍vector常用的成员函数有关vector定义的函数vector的迭代器使用vector关于空间操作的成员函数vector的增删查改 总结 vector介绍 在C语言的库中包含有公共数据结构的实现,C的这个部分内容就是众所周知的STL(标准模版库)&a…...
)
目标检测YOLO实战应用案例100讲-基于深度学习的交通场景多尺度目标检测算法研究与应用(下)
目录 3.2 基于空洞卷积的特征融合模块设计 3.3 改进k-means聚类算法的anchor尺寸优化设计...

react 类组件 和 函数组件 声明周期 对比
React 的类组件和函数组件在生命周期方面存在一些差异。以下是它们之间的对比: 类组件的生命周期 React 类组件的生命周期可以分为三个阶段:挂载、更新和卸载。 1、挂载阶段: constructor():组件实例化时调用,用于…...
智慧变电站守护者:TSINGSEE青犀AI视频智能管理系统引领行业革新
一、方案概述 随着科技的不断进步,人工智能(AI)技术已经深入到各个领域。在变电站安全监控领域,引入AI视频监控智能分析系统,可以实现对站内环境、设备状态的实时监控与智能分析,从而提高变电站的安全运行…...

【Ubuntu20.04安装java-8-openjdk】
1 下载 官网下载链接: https://www.oracle.com/java/technologies/downloads/#java8 下载 最后一行 jdk-8u411-linux-x64.tar.gz,并解压: tar -zxvf jdk-8u411-linux-x64.tar.gz2 环境配置 1、打开~/.bashrc文件 sudo gedit ~/.bashrc2、…...
HTTPS对于网站到底价值几何?
现在HTTPS基本上已经是网站的标配了,很少会遇到单纯使用HTTP的网站。但是十年前这还是另一番景象,当时只有几家大型互联网公司的网站会使用HTTPS,大部分使用的都还是简单的HTTP,这一切是怎么发生的呢? 为什么要把网站…...

Docker私有仓库Harbor
简介 Docker私有仓库Harbor是一个开源的、企业级的Docker registry解决方案,它提供了安全、可靠和高效的容器镜像存储和分发服务。以下是关于Docker私有仓库Harbor的详细介绍: 一、Harbor的特点 基于角色的访问控制(RBAC)&#…...

48. 旋转图像/240. 搜索二维矩阵 II
48. 旋转图像 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 示例 : 输入:matrix [[5,1,9,11],[2,4,…...

wsl安装Xfce桌面并设置系统语言和输入法
一、安装xfce (有相关的依赖都会安装) sudo apt -y install xfce4 二、 安装远程连接组件 sudo apt install xrdp -y 并重新启动 Xrdp 服务: sudo systemctl restart xrdp 本地windows系统中请按 winR 键 呼出运行 在运行中输入 mstsc…...
短信清空了!华为手机短信删除了怎么恢复?
“有没有人知道这是怎么回事呀,原先有一千多条未读一直放着没管,昨天根本没打开短信这个软件,今晚突然发现只剩一条了,是华为手机自动清理了吗!到底该怎么恢复呀?我真崩溃!” 在日常生活中&…...
Linux实现Flappy bird项目
目录 1、项目介绍 2、功能总结 3、前期准备 3.1 Ncurses库 3.2 信号机制 3.2.1 设置信号响应方式 3.2.2 设置定时器 4、代码实现 4.1 头文件引用及变量、函数定义 4.2 主函数 4.3 curses初始化 4.4 设置定时器 4.5 定时器响应函数 4.6 小鸟控制相关函数 4…...

【python量化交易】qteasy使用教程07——创建更加复杂的自定义交易策略
创建更加复杂的自定义交易策略 使用交易策略类,创建更复杂的自定义策略开始前的准备工作本节的目标继承Strategy类,创建一个复杂的多因子选股策略策略和回测参数配置,并开始回测 本节回顾 使用交易策略类,创建更复杂的自定义策略 …...
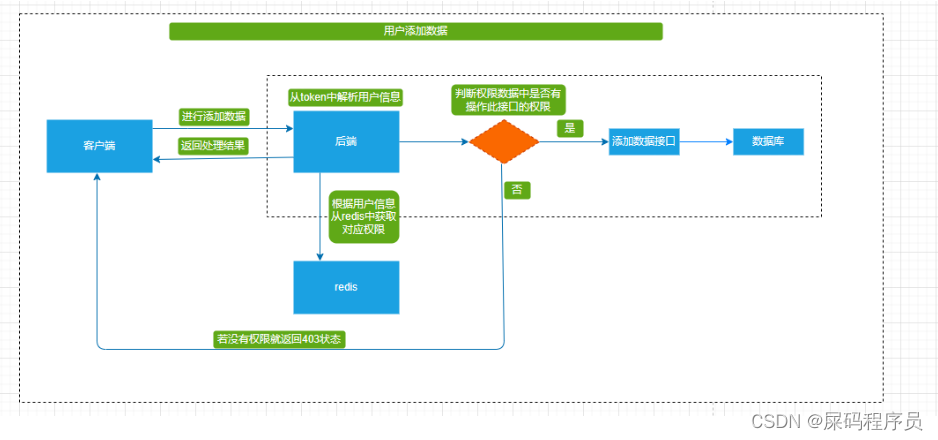
SpringBoot整合SpringScurity权限控制(菜单权限,按钮权限)以及加上SSH实现安全传输
文章目录 项目地址: 一、md5 与 先进的哈希算法的区别1.1. 安全性问题1.2. 设计目的1.3. 功能特性1.4. 适用性1.5. 总结 二、数据传输安全和数据加密实现:2.1 生成证书:2.2、在springboot中进行集成2.2.1 配置证书:2.2.2. 强制使用…...
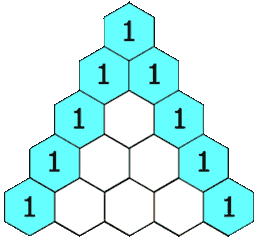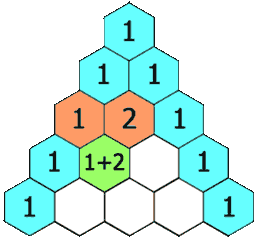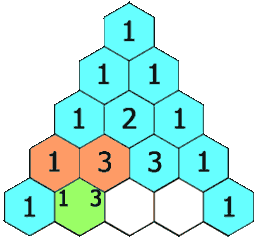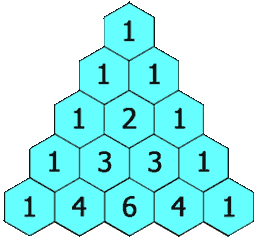
力扣每日一题119:杨辉三角||
题目 简单 给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: rowIndex 3 输出: [1,3,3,1]示例 2: 输入: rowIndex 0 输出: [1]示例 3: 输入: rowIndex 1 输出…...

AI语音模型PaddleSpeech踩坑(安装)指南
PaddleSpeech简介 PaddleSpeech 是基于飞桨 PaddlePaddle 的语音方向的开源模型库,用于语音和音频中的各种关键任务的开发,包含大量基于深度学习前沿和有影响力的模型。 PaddleSpeech安装步骤 提示:要找到一个合适的PaddleSpeech版本与pad…...
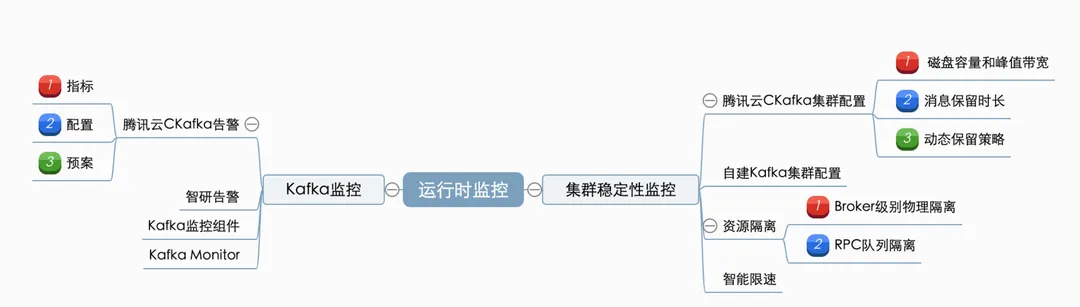
如何更好地使用Kafka? - 运行监控篇
要确保Kafka在使用过程中的稳定性,需要从kafka在业务中的使用周期进行依次保障。主要可以分为:事先预防(通过规范的使用、开发,预防问题产生)、运行时监控(保障集群稳定,出问题能及时发现&#…...
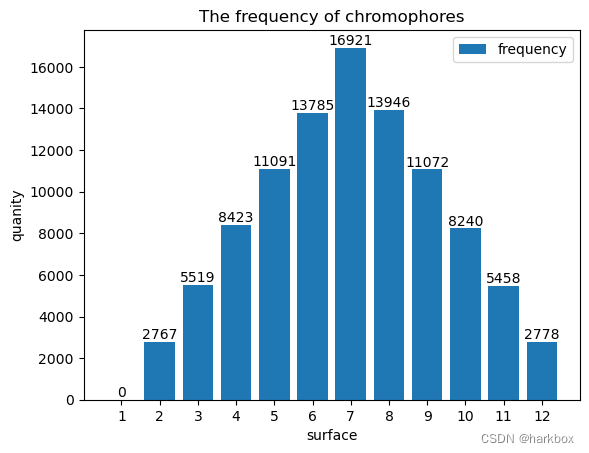
数据可视化训练第四天(模拟投掷筛子并且统计频次)
投掷一个筛子 import matplotlib.pyplot as plt from random import randint import numpy as npclass Die:"""模拟投掷筛子"""def __init__(self,num_sides6):self.num_sidesnum_sidesdef roll(self):return randint(1,self.num_sides)num1000…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
