算法设计课第五周(贪心法实现活动选择问题)
目录
一、【实验目的】
二、【实验内容】
三、实验源代码
一、【实验目的】
(1)熟悉贪心法的设计思想
(2)理解贪心法的最优解与正确性证明之间的关系
(3)比较活动选择的各种“贪心”策略,探讨最优算法。
二、【实验内容】
有n项活动申请使用同一场所,每项活动有一个开始和结束时间,如果任何两个活动不能重叠,问如何选择这些活动,使得被安排活动数量达到最多。
要求选择两项“贪心”策略进行比较,其中一个是最优的。建议最优算法参考教材P88的算法4.1.同时可以采用教材例4.1的数据进行验证。
三、实验源代码
#include <bits/stdc++.h>
using namespace std;
//有n个需要在同一天使用同一个教室的活动a1, a2, …, an,
//教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi。
//一旦被选择后,活动ai就占据半开时间区间[si, fi)。如果[si, fi]和[sj, fj]互不重叠,
//ai和aj两个活动就可以被安排在这一天。
//该问题就是要安排这些活动使得尽量多的活动能不冲突的举行。《算法导论》struct activity
{int start;int end;
}a[200];int n;
vector<activity> set1, set2;//比较函数,按结束时间排序
bool cmp1(activity x, activity y)
{if (x.end == y.end)return x.start < y.start;//不能加等于号,会报错return x.end < y.end;
}
//比较函数,按开始时间排序
bool cmp2(activity x, activity y)
{return x.start < y.start;//不能加等于号,会报错
}int strategy1() //最佳策略
{sort(a, a + n, cmp1);int cnt = 1;//第一个活动已经选了,所以初始是1 (1,4)int j = 0;set1.push_back(a[0]);for (int i = 1; i < n; i++){if (a[j].end <= a[i].start){cnt++;j = i;set1.push_back(a[i]);}}return cnt;
}int strategy2() //按开始时间排序策略
{sort(a, a + n, cmp2);int cnt = 1;//第一个活动已经选了,所以初始是1 (0,6)int j = 0;set2.push_back(a[0]);for (int i = 1; i < n; i++){if (a[j].end <= a[i].start){cnt++;j = i;set2.push_back(a[i]);}}return cnt;
}int main()
{cin >> n;for (int i = 0; i < n; i++){cin >> a[i].start >> a[i].end;}cout << "策略1选择活动数量:" << strategy1() << endl;cout << "活动为:";for (auto& e : set1){cout << '(' << e.start << ',' << e.end << ") ";}cout << endl;cout << "策略2选择活动数量:" << strategy2() << endl;cout << "活动为:";for (auto& e : set2){cout << '(' << e.start << ',' << e.end << ") ";}
}
/*
input:
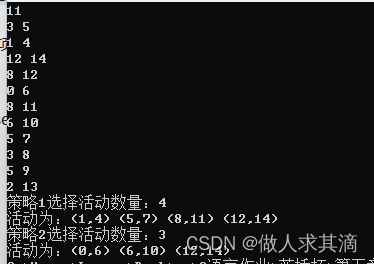
11
3 5
1 4
12 14
8 12
0 6
8 11
6 10
5 7
3 8
5 9
2 13
*/【输出结果】
相关文章:

算法设计课第五周(贪心法实现活动选择问题)
目录 一、【实验目的】 二、【实验内容】 三、实验源代码 一、【实验目的】 (1)熟悉贪心法的设计思想 (2)理解贪心法的最优解与正确性证明之间的关系 (3)比较活动选择的各种“贪心”策略,…...
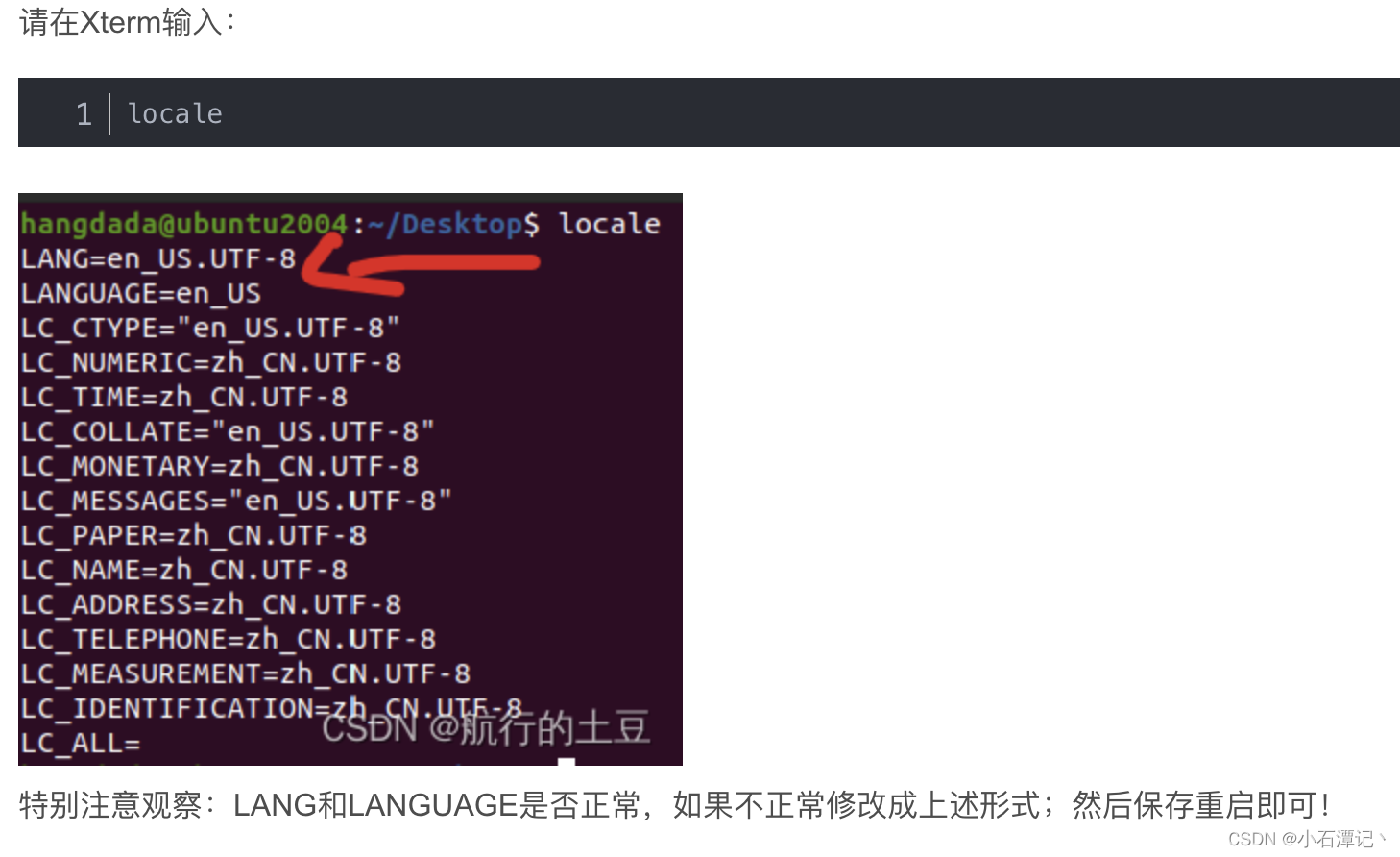
Ubuntu20.04右键打不开终端
今天用virtualbox安装了ubuntu20.04 问题:右键打开终端,怎么也打开不了! 点了也没反应,或者鼠标转小圈圈,然后也没有反应… 解决方法: 1、Ctrl Alt F6 先切换到终端访问界面 mac电脑 Ctrl Alt F6 …...

XML元素
XML 元素是XML文档中的基本组成单位,它由开始标签、结束标签和内容组成,格式如下: <element>content</element>常见的XML元素包括: 根元素(Root Element):XML文档中的最外层元素&…...
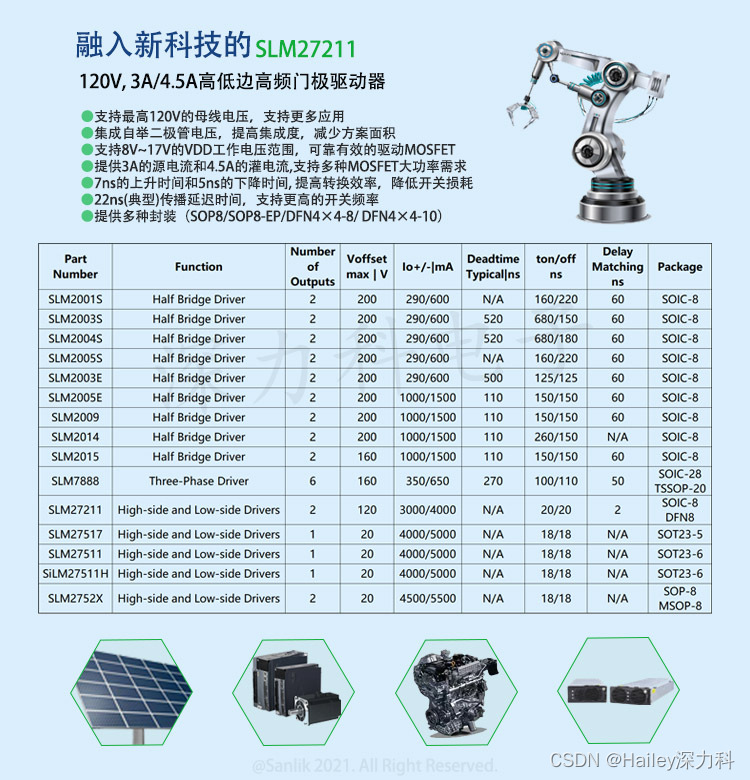
融入新科技的SLM27211系列 120V, 3A/4.5A高低边高频门极驱动器兼容UCC27284,MAX15013A
SLM27211是高低边高频门极驱动器,集成了120V的自举二极管,支持高频大电流的输出,可在8V~17V的宽电压范围内驱动MOSFET,独立的高、低边驱动以方便控制,可用于半桥、全桥、双管正激和有源钳位正激等拓。有极好的开通、关…...
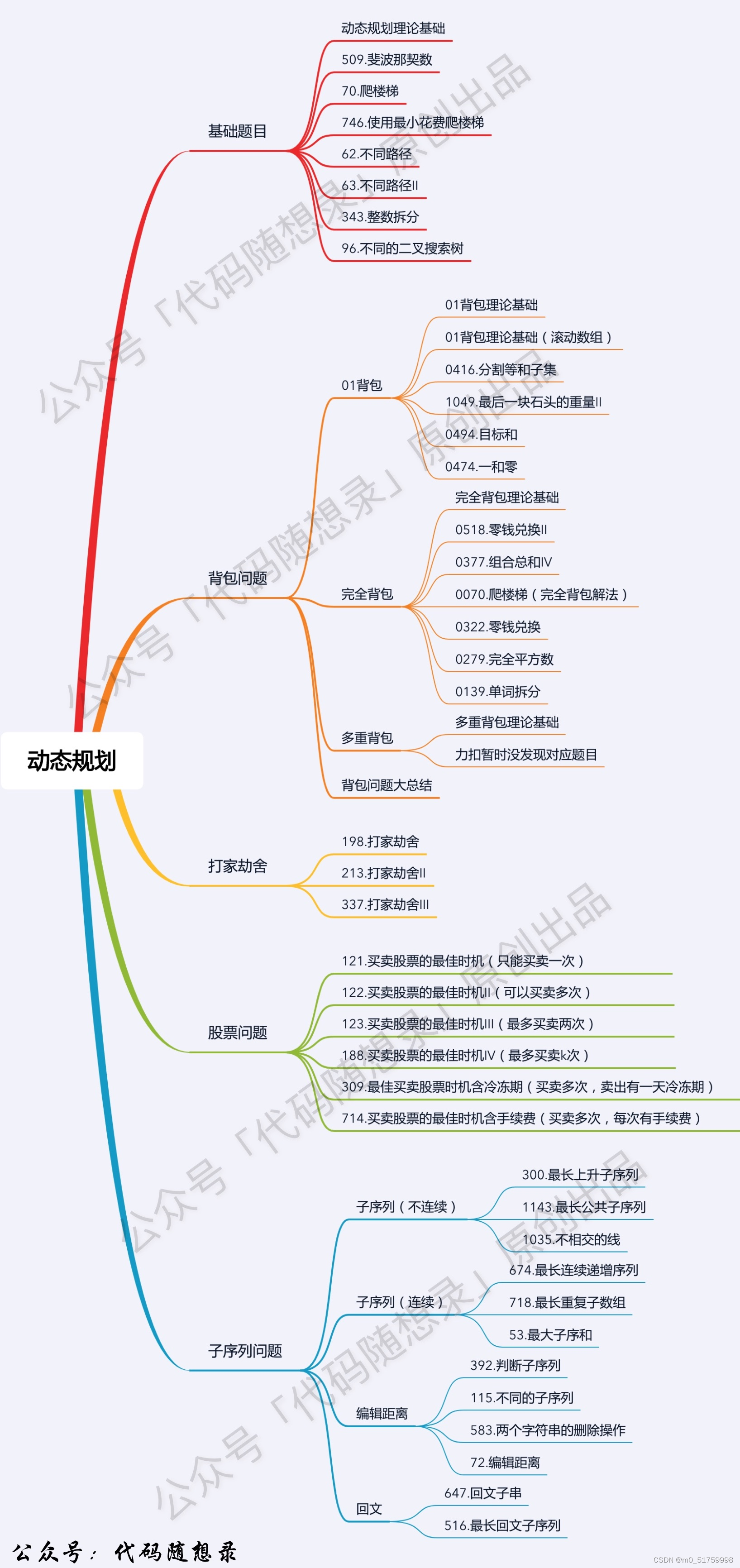
代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯 文章目录 代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯理论基础一、常规题目二、解题步骤…...

CSS拟物按钮
<div class"btn">F</div>.btn {margin: 150px 0 0 150px;display: flex;justify-content: center;align-items: center;width: 100px;height: 100px;background-color: #fff;border-radius: 20px;font-size: 50px;color: #333;/* 禁止选中文本 */user-se…...

websevere服务器从零搭建到上线(三)|IO多路复用小总结和服务器的基础框架
文章目录 epollselect和poll的优缺点epoll的原理以及优势epoll 好的网络服务器设计Reactor模型图解Reactor muduo库的Multiple Reactors模型 epoll select和poll的优缺点 1、单个进程能够监视的文件描述符的数量存在最大限制,通常是1024,当然可以更改数…...
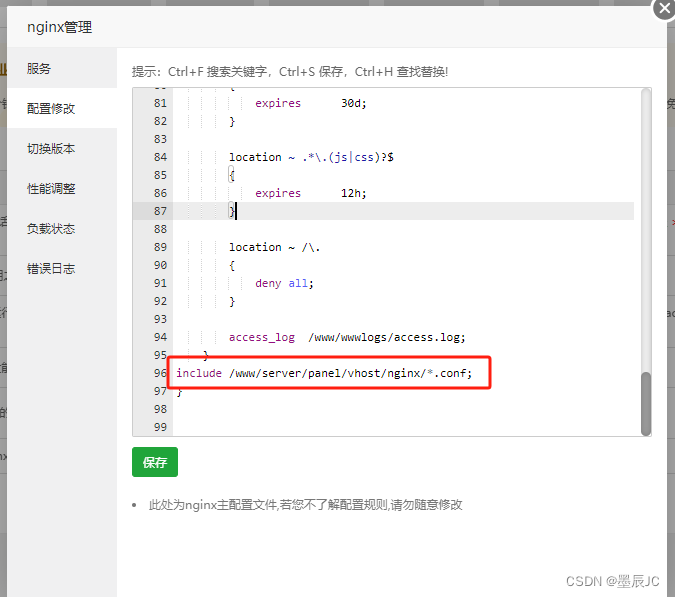
解决宝塔Nginx和phpMyAdmin配置端口冲突问题
问题描述 在对基于宝塔面板的 Nginx 配置文件进行端口修改时,我注意到 phpMyAdmin 的端口配置似乎也随之发生了变化! 解决方法 官方建议在处理 Nginx 配置时,应避免直接修改默认的配置文件,以确保系统的稳定性和简化后续的维护…...
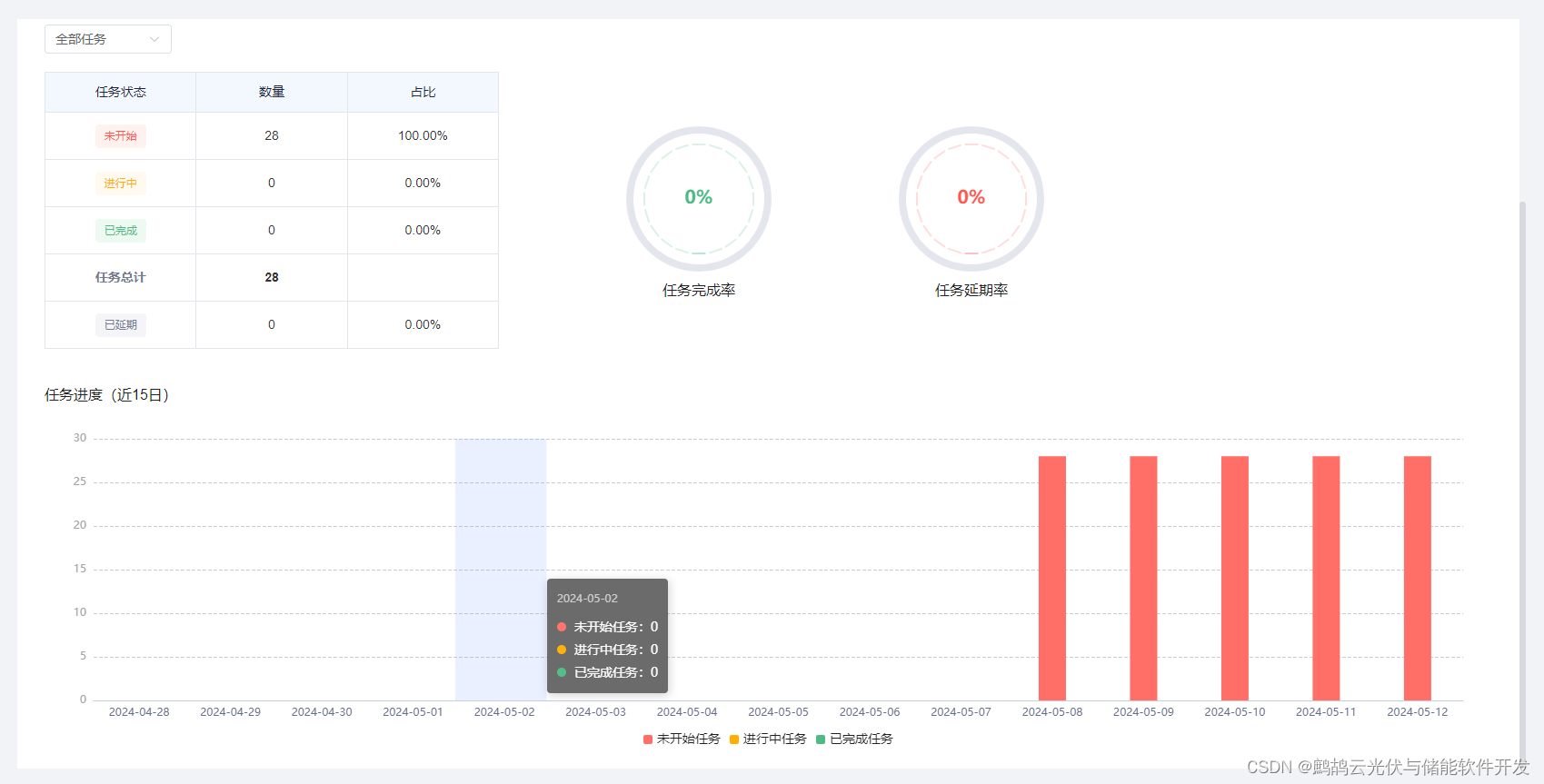
光伏EPC管理软件都有哪些功能和作用?
光伏EPC管理软件是用于光伏工程项目管理的综合性工具,它涵盖了从项目策划、设计、采购、施工到运维的各个环节。 1、项目总览 管理所有项目计划,包括项目类型、项目容量等。 调整和优化项目计划,以应对不可预见的情况。 2、施工管理 制定…...
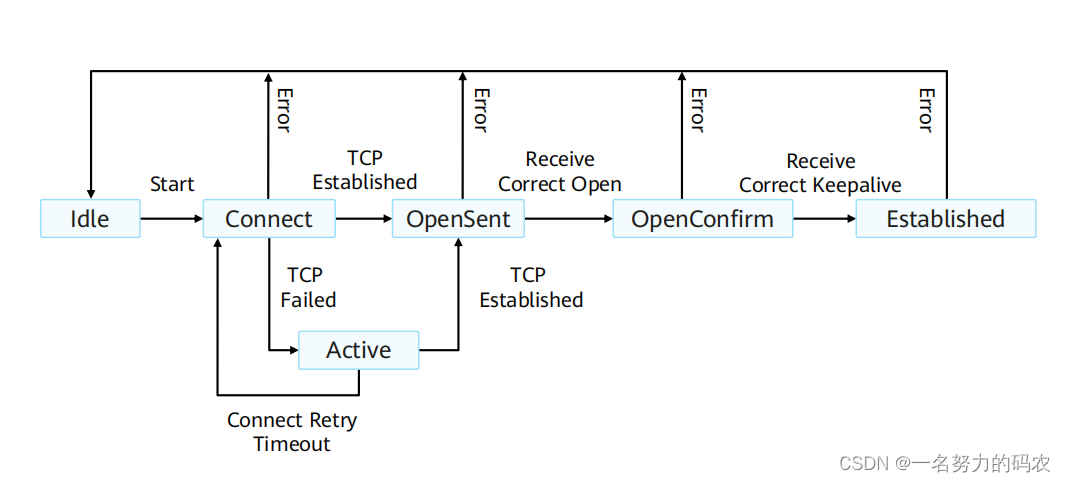
BGP学习一:关于对等体建立和状态组改变
目录 一.BGP基本概念 (1).BGP即是协议也是分类 1.早期EGP 2.BGP满足不同需求 3.BGP区域间传输的优势 (1)安全性——只传递路由信息 (2)跨网段建立邻居 4.BGP总结 5.BGP的应用 (1&#…...
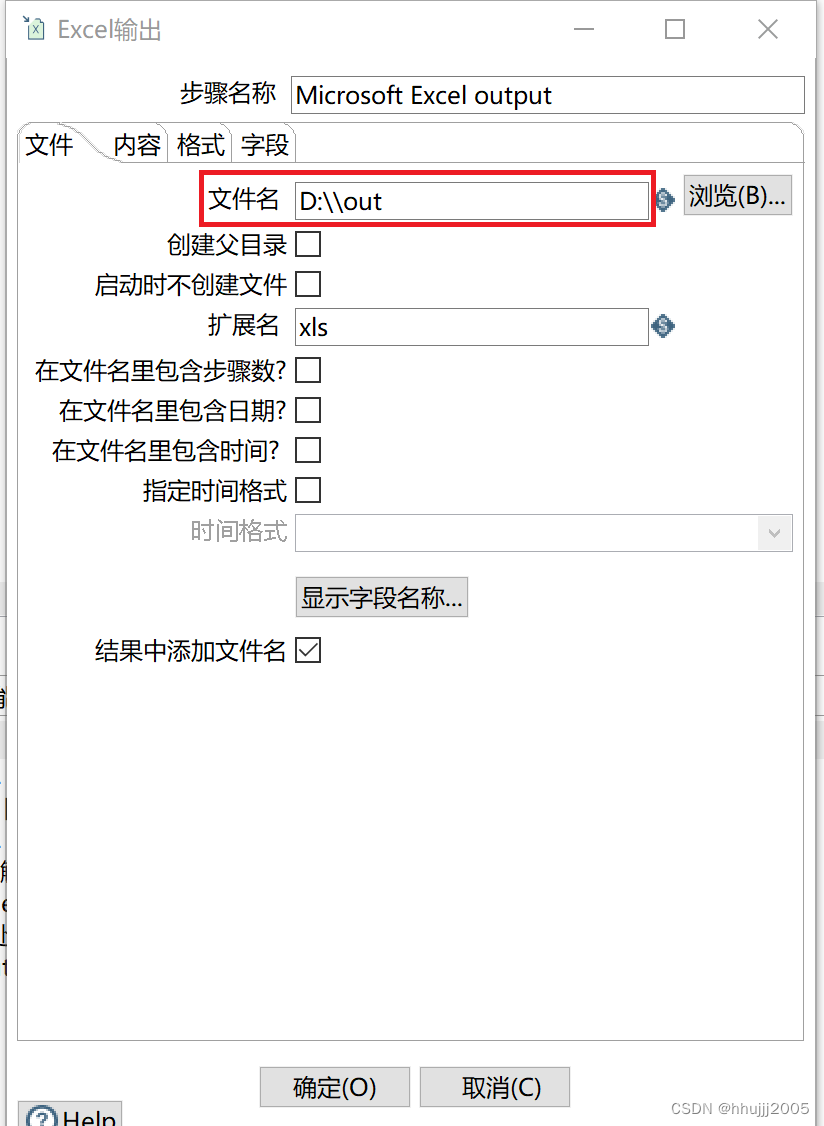
ETL工具kettle(PDI)入门教程,Transform,Mysql->Mysql,Csv->Excel
什么是kettle,kettle的下载,安装和配置:ETL免费工具kettle(PDI),安装和配置-CSDN博客 mysql安装配置:Linux Centos8 Mysql8.3.0安装_linux安装mysql8.3-CSDN博客 1 mysql -> mysql 1.1 mysql CREATE TABLE user_…...

常见地图坐标系间的转换算法JavaScript实现
文章目录 🍉 不同的地图厂商使用不同的坐标系来表示地理位置。以下简述:🍉 前置常量和方法:🍉 BD-09转GCJ-02(百度转谷歌、高德)🍉 GCJ-02转BD-09(谷歌、高德转百度)🍉 WGS84转GCJ-02(WGS84转谷歌、高德)🍉 GCJ-02转WGS84(谷歌、高德转WGS84)🍉 BD-09转wgs84坐…...

基于python的大麦网自动抢票工具的设计与实现
基于python的大麦网自动抢票工具的设计与实现 Design and Implementation of Da Mai Net Ticket Grabbing tool based on Python 完整下载链接:基于python的大麦网自动抢票工具的设计与实现 文章目录 基于python的大麦网自动抢票工具的设计与实现摘要第一章 引言1.1 研究背景…...

2024年5月树莓集团快讯
树莓集团近期快讯 1 园区专场招聘会进校园 国际数字影像产业园联合四川城市职业学院的专场招聘会成功召开,共计提供400余个工作岗位。 2 园区硬件优化再升级 园区硬件优化再升级,智能门禁系统及人脸识别系统下周投入使用。 3 基地短剧合作交流 天府…...

网站localhost和127.0.0.1可以访问,本地ip不可访问解决方案
部署了一个网站, 使用localhost和127.0.0.1加端口号可以访问, 但是使用本机的ip地址加端口号却不行. 原因可能有多种. 可能的原因: 1 首先要确认是否localhost对应的端口是通的(直接网址访问), 以及你无法访问的那个本机ip是否正确(使用ping测试); 2 检查本机的防火…...

Docker Dockerfile如何编写?
Dockerfile 是一个用来构建镜像的文本文件,文本内容包含了一条条构建镜像所需的指令和说明。 1.指令说明 FROM,构建镜像基于哪个镜像 MAINTAINER,镜像维护者姓名或邮箱地址 RUN,构建镜像时运行的指令 CMD,运行容器时执…...

Python数独游戏
数独(Sudoku)是一种逻辑性的数字填充游戏,玩家需要在一个分为九宫的81格网格上填入数字,同时满足每一行、每一列以及每个宫(3x3的子网格)的数字都不重复。 在Python中实现一个数独游戏可以涉及到多个方面&…...
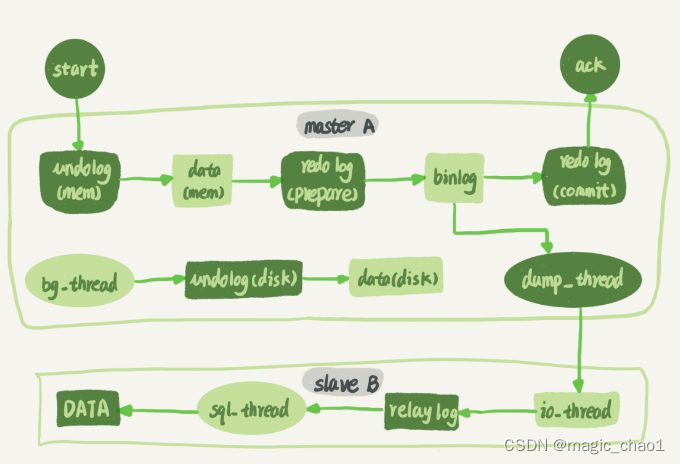
24 | MySQL是怎么保证主备一致的?
MySQL 主备的基本原理 内部流程 备库 B 跟主库 A 之间维持了一个长连接。主库 A 内部有一个线程,专门用于服务备库 B 的这个长连接。一个事务日志同步的完整过程是这样的: 在备库 B 上通过 change master 命令,设置主库 A 的 IP、端口、用户名、密码,以及要从哪个位置开始…...

2.数据类型与变量(java篇)
目录 数据类型与变量 数据类型 变量 整型变量 长整型变量 短整型变量 字节型变量 浮点型变量 双精度浮点型 单精度浮点型 字符型变量 布尔型变量(boolean) 类型转换 自动类型转换(隐式) 强制类型转换(显式) 类型提升 字符串类型 数据类…...

QT设计模式:桥接模式
基本概念 桥接模式是一种结构型设计模式,它将抽象部分与它的实现部分分离,使得它们可以独立地变化,而不会相互影响。 需要实现的结构如下: 抽象部分(Abstraction):定义了抽象类的接口&#x…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
