Offer必备算法38_贪心算法四_八道力扣题详解(由易到难)
目录
①力扣56. 合并区间
解析代码
②力扣435. 无重叠区间
解析代码
③力扣452. 用最少数量的箭引爆气球
解析代码
④力扣397. 整数替换
解析代码1_递归改记忆化搜索
解析代码2_贪心策略
⑤力扣354. 俄罗斯套娃信封问题
解析代码1_动态规划(超时)
解析代码2_重写排序+贪心+二分
⑥力扣1262. 可被三整除的最大和
解析代码
⑦力扣1054. 距离相等的条形码
解析代码
⑧力扣767. 重构字符串
解析代码
本篇完。
①力扣56. 合并区间
56. 合并区间
难度 中等
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 10^4intervals[i].length == 20 <= starti <= endi <= 10^4
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {}
};解析代码
贪心策略:
- 先按照区间的左端点排序:此时会发现能够合并的区间都是连续的。
- 然后从左往后,如果可以合并就按照求并集的方式合并区间,如果不可以合并就把区间丢到结果数组,再往后遍历。
如何求并集:
由于区间已经按照左端点排过序了,因此当两个区间合并的时候,合并后的区间:
- 左端点就是前一个区间的左端点。
- 右端点就是两者右端点的最大值。
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(), intervals.end());vector<vector<int>> ret;int left = intervals[0][0], right = intervals[0][1];for(auto& e : intervals){if(e[0] <= right) // 可以合并{right = max(right, e[1]);}else{ret.push_back({left, right});left = e[0], right = e[1];}}ret.push_back({left, right});return ret;}
};
②力扣435. 无重叠区间
435. 无重叠区间
难度 中等
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
提示:
1 <= intervals.length <= 10^5intervals[i].length == 2-5 * 10^4 <= starti < endi <= 5 * 10^4
class Solution {
public:int eraseOverlapIntervals(vector<vector<int>>& intervals) {}
};解析代码
贪心策略:
- 先按照区间的左端点排序。
- 当两个区间重叠的时候,为了能够在移除某个区间后,保留更多的区间,我们应该把区间范围较大的区间移除。
如何移除区间范围较大的区间:
由于已经按照左端点排序了,因此两个区间重叠的时候,我们应该保留右端点较小的区间。
class Solution {
public:int eraseOverlapIntervals(vector<vector<int>>& intervals) {sort(intervals.begin(), intervals.end());int ret = 0;int left = intervals[0][0], right = intervals[0][1];for(auto& e : intervals){if(e[0] >= right) // 不重叠{left = e[0], right = e[1];}else // 重叠{++ret;right = min(right, e[1]); // 保留右端点较小的区间}}return ret - 1; // 从第一个区间开始比较就删掉第一个区间}
};
③力扣452. 用最少数量的箭引爆气球
452. 用最少数量的箭引爆气球
难度 中等
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:气球可以用2支箭来爆破: -在x = 6处射出箭,击破气球[2,8]和[1,6]。 -在x = 11处发射箭,击破气球[10,16]和[7,12]。
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]] 输出:4 解释:每个气球需要射出一支箭,总共需要4支箭。
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2 解释:气球可以用2支箭来爆破: - 在x = 2处发射箭,击破气球[1,2]和[2,3]。 - 在x = 4处射出箭,击破气球[3,4]和[4,5]。
提示:
1 <= points.length <= 105points[i].length == 2-2^31 <= xstart < xend <= 2^31 - 1
class Solution {
public:int findMinArrowShots(vector<vector<int>>& points) {}
};解析代码
贪心策略:
- 先按照区间的左端点排序:此时会发现互相重叠的区间都是连续的。
- 这样在射箭的时候,要发挥每一支箭最大的作用,应该把互相重叠的区间统一引爆。
如何求互相重叠区间:
由于我们是按照左端点排序的,因此对于两个区间,我们求的是它们的交集:(注意合并区间用的是并集,求重叠区间求的是交集)
- 左端点为两个区间左端点的最大值,但是左端点不会影响我们的合并结果,所以可以忽略。
- 右端点为两个区间右端点的最小值。
class Solution {
public:int findMinArrowShots(vector<vector<int>>& points) {sort(points.begin(), points.end());int ret = 1, right = points[0][1];for(auto& e : points){if(e[0] <= right) // 能合并,求交集,一起击破{// left = max(left, e[0]); // left不影响合并结果right = min(right, e[1]);}else // 不能合并,继续往后遍历{++ret;// left = e[0]; // left不影响合并结果right = e[1];}}return ret; // 加上最后的区间}
};
④力扣397. 整数替换
397. 整数替换
难度 中等
给定一个正整数 n ,你可以做如下操作:
- 如果
n是偶数,则用n / 2替换n。 - 如果
n是奇数,则可以用n + 1或n - 1替换n。
返回 n 变为 1 所需的 最小替换次数 。
示例 1:
输入:n = 8 输出:3 解释:8 -> 4 -> 2 -> 1
示例 2:
输入:n = 7 输出:4 解释:7 -> 8 -> 4 -> 2 -> 1 或 7 -> 6 -> 3 -> 2 -> 1
示例 3:
输入:n = 4 输出:2
提示:
1 <= n <= 2^31 - 1
class Solution {
public:int integerReplacement(int n) {}
};解析代码1_递归改记忆化搜索
此题的贪心策略很难想出来,先看看记忆化搜索的方法(记忆化搜索在之前专题已经学过):用爆搜模拟也可以过,但是加上备忘录优化:
class Solution {unordered_map<int, int> memo;
public:int integerReplacement(int n) {// 时间O(logN) 空间O(logN)return dfs(n);}int dfs(long long n){if(n == 1)return 0;if(memo[n] != 0)return memo[n];if(n % 2 == 0){memo[n] = 1 + dfs(n / 2);return memo[n];}else{memo[n] = 1 + min(dfs(n - 1), dfs(n + 1));return memo[n];}}
};
解析代码2_贪心策略
贪心策略:任何选择都应该让这个数尽可能快地变成 1 。
- 对于偶数:只执行除 2 操作。
- 对于奇数:
- 当 n== 1 的时候,不用执行任何操作。
- 当 n == 3 的时候,变成 1 的最优操作数是 2 。
- 当 n > 1 && n % 4 == 1的时候,那么它的二进制表示是 ......01 ,最优的方式应该选择 -1 ,这样就可以把末尾的 1 干掉,接下来执行除法操作,能够更快地变成1 。
- 当 n > 3 && n % 4 == 3的时候,那么它的二进制表示是 ......11 ,最优的方式应该选择 +1 ,这样可以把一堆连续的 1 转换成 0 ,更快地变成 1 。
class Solution {
public:int integerReplacement(int n){// 时间O(logN) 空间O(1)int ret = 0;while(n != 1){if(n % 2 == 0){n = n / 2;++ret;}else{ret += 2; // 下面操作都是两步if(n == 3)break;else if(n % 4 == 1) // ......01n /= 2; // 和减1除2结果一样else // ......01n = n / 2 + 1; // 和加1除2结果一样,防溢出}}return ret;}
};
⑤力扣354. 俄罗斯套娃信封问题
354. 俄罗斯套娃信封问题
难度 困难
给你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。
当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
注意:不允许旋转信封。
示例 1:
输入:envelopes = [[5,4],[6,4],[6,7],[2,3]] 输出:3 解释:最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
示例 2:
输入:envelopes = [[1,1],[1,1],[1,1]] 输出:1
提示:
1 <= envelopes.length <= 10^5envelopes[i].length == 21 <= wi, hi <= 10^5
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {}
};解析代码1_动态规划(超时)
将数组按照左端点排序之后,问题就转化成了最长递增子序列模型,那接下来我们就可以用解决最长递增子序列的经验,来解决这个问题(会超时,但还是建议敲一下代码)。
- 状态表示:dp[i] 表示:以 i 位置的信封为结尾的所有套娃序列中,最长的套娃序列的长度。
- 状态转移方程:dp[i] = max(dp[j] + 1) 其中 0 <= j < i && e[i][0] > e[j][0] && e[i][1] > e[j][1] 。
- 初始化:全部初始化为 1 。
- 填表顺序:从左往右。
- 返回值:整个 dp 表中的最大值。
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end());int n = envelopes.size(), ret = 1;vector<int> dp(n, 1);for(int i = 1; i < n; ++i){for(int j = 0; j < i; ++j){if(envelopes[i][0] > envelopes[j][0] && envelopes[i][1] > envelopes[j][1]){dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]);}return ret;}
};
解析代码2_重写排序+贪心+二分
当我们把整个信封按照下面的规则排序之后:
- 左端点不同的时候:按照左端点从小到大排序。
- 左端点相同的时候:按照右端点从大到小排序
此时问题就变成了仅考虑信封的右端点,完完全全的变成的最长递增子序列的模型。那么我们就可以用贪心 + 二分优化我们的算法。
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end(), [&](vector<int>& e1, vector<int>& e2){return e1[0] != e2[0] ? e1[0] < e2[0] : e1[1] > e2[1];});vector<int> ret;ret.push_back(envelopes[0][1]);for(auto& e : envelopes){if(e[1] > ret.back()){ret.push_back(e[1]);}else // 二分找到要放的位置(找大于等于e[1]的左端点){int left = 0, right = ret.size() - 1;while(left < right){int mid = (left + right) >> 1;if(ret[mid] < e[1])left = mid + 1;elseright = mid;}ret[left] = e[1];}}return ret.size();}
};
⑥力扣1262. 可被三整除的最大和
1262. 可被三整除的最大和
难度 中等
给你一个整数数组 nums,请你找出并返回能被三整除的元素最大和。
示例 1:
输入:nums = [3,6,5,1,8] 输出:18 解释:选出数字 3, 6, 1 和 8,它们的和是 18(可被 3 整除的最大和)。
示例 2:
输入:nums = [4] 输出:0 解释:4 不能被 3 整除,所以无法选出数字,返回 0。
示例 3:
输入:nums = [1,2,3,4,4] 输出:12 解释:选出数字 1, 3, 4 以及 4,它们的和是 12(可被 3 整除的最大和)。
提示:
1 <= nums.length <= 4 * 10^41 <= nums[i] <= 10^4
class Solution {
public:int maxSumDivThree(vector<int>& nums) {}
};解析代码
正难则反: 可以先把所有的数累加在一起,然后根据累加和的结果,贪心地删除一些数。
分类讨论:设累加和为 sum ,用 x 标记 %3 == 1 的数,用 y 标记 % 3 == 2 的数。那么根据 sum 的余数,可以分为下面三种情况:(求最小的值和次小的值可以直接sort,也可以在求数组和的时候记录下来,时间就变为了O(N))。
- sum % 3 == 0 ,此时所有元素的和就是满足要求的,直接返回。
- sum % 3 == 1,此时数组中要么存在一个x(x % 3 == 1),要么存在两个y(y % 3 == 2)。因为我们要的是最大值,所以应该选择 x 中最小的那么数,记为 x1 ,或者是 y 中最小以及次小的两个数,记为 y1, y2 。那么,我们应该选择这两种情况下的最大值: max(sum - x1, sum - y1 - y2) 。
- sum % 3 == 2,此时数组中要么存在一个 y(y % 3 == 2),要么存在两个 x(x % 3 == 1) 。因为我们要的是最大值,所以应该选择 y 中最小的那个数,记为 y1 ,或者是 x 中最小以及次小的两个数,记为 x1, x2 。那么,我们应该选择这两种情况下的最大值: max(sum - y1, sum - x1 - x2) 。
那么应该选择下面两种情况下的最大值: max(sum - y1, sum - x1 - x2) ;
class Solution {
public:int maxSumDivThree(vector<int>& nums) {const int INF = 0x3f3f3f3f;int sum = 0, x1 = INF, x2 = INF, y1 = INF, y2 = INF;for(auto& x : nums){sum += x;if(x % 3 == 1) // 找出x % 3 == 1中x最小的和次小的{if(x < x1)x2 = x1, x1 = x;else if(x < x2) x2 = x;}else if(x % 3 == 2) // 找出x % 3 == 2中x最小的和次小的{if(x < y1)y2 = y1, y1 = x;else if(x < y2)y2 = x;}}if(sum % 3 == 1)sum = max(sum - x1, sum - y1 - y2);else if(sum % 3 == 2)sum = max(sum - y1, sum - x1 - x2);return sum;}
};
⑦力扣1054. 距离相等的条形码
1054. 距离相等的条形码
难度 中等
在一个仓库里,有一排条形码,其中第 i 个条形码为 barcodes[i]。
请你重新排列这些条形码,使其中任意两个相邻的条形码不能相等。 你可以返回任何满足该要求的答案,此题保证存在答案。
示例 1:
输入:barcodes = [1,1,1,2,2,2] 输出:[2,1,2,1,2,1]
示例 2:
输入:barcodes = [1,1,1,1,2,2,3,3] 输出:[1,3,1,3,2,1,2,1]
提示:
1 <= barcodes.length <= 100001 <= barcodes[i] <= 10000
class Solution {
public:vector<int> rearrangeBarcodes(vector<int>& barcodes) {}
};解析代码
贪心策略:
- 每次处理一批相同的数字,往 n 个空里面摆放。
- 每次摆放的时候,隔一个格子摆放一个数。
- 先处理出现次数最多的那个数,剩下的数可任意。此题保证存在答案->出现次数最多的那个数不会超过(n + 1)/ 2,下一个数想相邻的话只能“填一圈”(不可能)。
class Solution {
public:vector<int> rearrangeBarcodes(vector<int>& barcodes) {unordered_map<int, int> hash; // 数和其出现的次数int mostVal = 0, maxCount = 0;for(auto& e : barcodes) // 统计每个数出现的频次{++hash[e];if(maxCount < hash[e]){maxCount = hash[e];mostVal = e;}}int n = barcodes.size(), index = 0;vector<int> ret(n);for(int i = 0; i < maxCount; ++i) // 先处理出现次数最多的数{ret[index] = mostVal;index += 2;}hash.erase(mostVal);for(auto& [a, b] : hash) // 处理剩下的数{for(int i = 0; i < b; ++i){if(index >= n)index = 1;ret[index] = a;index += 2;}}return ret;}
};
⑧力扣767. 重构字符串
767. 重构字符串
难度 中等
给定一个字符串 s ,检查是否能重新排布其中的字母,使得两相邻的字符不同。
返回 s 的任意可能的重新排列。若不可行,返回空字符串 "" 。
示例 1:
输入: s = "aab" 输出: "aba"
示例 2:
输入: s = "aaab" 输出: ""
提示:
1 <= s.length <= 500s只包含小写字母
class Solution {
public:string reorganizeString(string s) {}
};解析代码
和力扣1054. 距离相等的条形码基本一致。
贪心策略:
- 每次处理一批相同的字母,往 n 个空里面摆放。
- 每次摆放的时候,隔一个格子摆放一个字母。
- 先处理出现次数最多的那个字母,剩下的字母可任意。如果出现次数最多的那个字母不超过(n + 1)/ 2,则有解,下一个字母想相邻的话只能“填一圈”(不可能)。
class Solution {
public:string reorganizeString(string s) {int hash[26] = {0};char mostVal = s[0];int maxCount = 0;for(auto& e : s) // 统计每个数出现的频次{++hash[e - 'a'];if(maxCount < hash[e - 'a']){maxCount = hash[e - 'a'];mostVal = e;}}int n = s.size(), index = 0;if(maxCount > (n + 1) / 2)return "";string ret(n, ' ');for(int i = 0; i < maxCount; ++i) // 先处理出现次数最多的数{ret[index] = mostVal;index += 2;}hash[mostVal - 'a'] = 0;for(int i = 0; i < 26; ++i) // 处理剩下的数{for(int j = 0; j < hash[i]; ++j){if(index >= n)index = 1;ret[index] = i + 'a';index += 2;}}return ret;}
};
本篇完。
此专栏暂时就不更新了,常见的算法的学了一遍了,先完结撒花,后面再更新高阶数据结构图等内容,然后更新力扣的每日一题或者更新一些牛客的题。
相关文章:

Offer必备算法38_贪心算法四_八道力扣题详解(由易到难)
目录 ①力扣56. 合并区间 解析代码 ②力扣435. 无重叠区间 解析代码 ③力扣452. 用最少数量的箭引爆气球 解析代码 ④力扣397. 整数替换 解析代码1_递归改记忆化搜索 解析代码2_贪心策略 ⑤力扣354. 俄罗斯套娃信封问题 解析代码1_动态规划(超时…...

java8 转对象,Java8转Map,Java8转Llist
1.准备数据 public static List<Persion> getData(){List<Persion> arrayList new ArrayList<>();arrayList.add(new Persion("李四","20","男"));arrayList.add(new Persion("王麻子","30","男&q…...

【Pytest官方文档翻译及学习】2.1 如何调用pytest
目录 2.1 如何调用pytest 2.1.1 指定要运行的测试 2.1.2 获取有关版本、选项名称、环境变量的帮助 2.1.3 分析测试执行时间 2.1.4 管理加载插件 2.1.5 调用pytest的其他方式 2.1 如何调用pytest 2.1.1 指定要运行的测试 Pytest支持几种从命令行运行和选择测试的方法。、…...
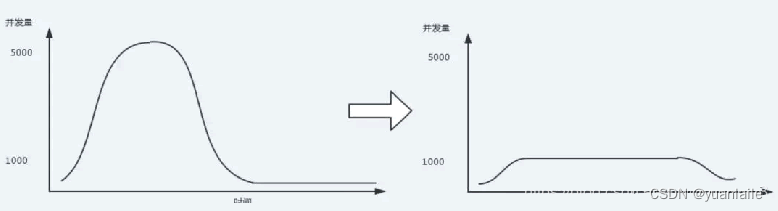
RabbitMQ的用途
RabbitMQ主要有四个用途,分别是应用解耦、异步提速、削峰填谷、消息分发。详情讲解如下: RabbitMQ介绍、解耦、提速、削峰、分发 详解、RabbitMQ安装 可视化界面讲解 1.应用解耦:提高系统容错性和可维护性 2.异步提速:提升用户体验…...
R语言软件安装及配置
1、下载 网址:www.r-project.org 1.1 下载R 选择download R 选择清华源进行下载 根据自己系统情况下载,我选择windows系统。 先选择base。 选择最新的版本下载。 1.2 下载RTools 下载好后,返回,选择RTools进入后,选…...

网络配置的加密存储
随着数据泄露事件的增加,扰乱了公司的正常工作周期,企业遭受了损失。事实上,数据泄露可以通过存储加密来控制,存储加密是防止黑客对网络数据库造成严重破坏的最有效方法之一。在网络配置管理器中,存储加密可用于存储设…...

你写代码,会关注时间复杂度吗?
虽然面试的时候总是被问到这个问题,但你写代码的时候,真的会想到这个问题吗?时间复杂度,说的当然不是你写的代码执行用了多长时间,而是代码执行语句的次数。 目录 每行代码都需要注意 计算方法 1 例如常量增长 2 …...
【连连国际注册/登录安全分析报告】
连连国际注册/登录安全分析报告 前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨…...
-远程访问)
linux进阶高级配置,你需要知道的有哪些(10)-远程访问
1、ssh协议的功能 为客户机提供安全的shell环境(字符界面),用于远程管理 2、openssh的服务说明 服务名:sshd 重启服务:systemctl restart sshd 主配置文件:/etc/ssh/sshd/_config 端口号:tcp 2…...

不显示 表格 style=“display: none;“ 这个默认是不显示的
不显示 表格 style“display: none;” 这个默认是不显示的 取消就可以或者 $(‘#modifyStatusBtn’).show(); <div id"userInfoContainer" style"display: none;"></div>...

Bittensor怎么挖?手把手教你,使用bitget钱包
4月 Binance 上新 TheBittensorHub (TAO), 这个项目究竟做了什么可以令其在上大舞台前就已经在所有通证中排名前 30? 本文将深度解析。 该项目既不直接贡献数据,也不直接贡献算力。 而是通过区块链网络和激励机制,来对不同的算法进行调度和…...

领略Java内部类的“内部”
内部类有两种情况: (1) 在类中定义一个类(私有内部类,静态内部类) (2) 在方法中定义一个类(局部内部类,匿名内部类) 1、私有内部类 —— 在方法之间定义的内部类,非静态 我们首先看看类中内部类的两个特点: (1) 在外部…...
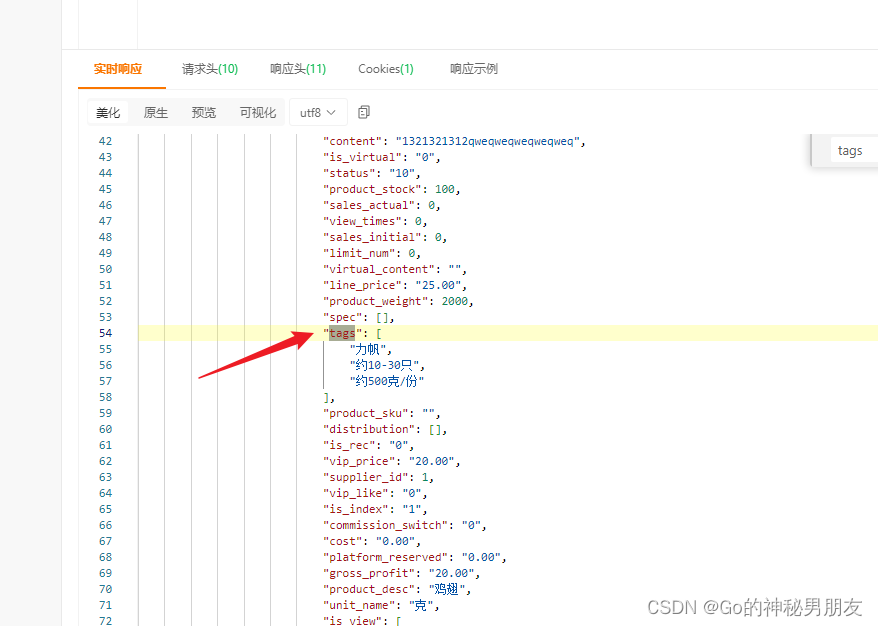
PHP 提取数组中的特定的值
需求: 前端展示: (1)之前的页面: (2)修改后的页面: 之前接口返回的数据 : 解决办法:提取tags 中的 ’约 的数组 添加到一个新的数组中去 1:一开…...

SpringBoot、JAVA中excel、rtf、doc转PDF
话不多说,直接上干货 // 官方文档的要求 无需理会public static boolean getLicense() {boolean result false;try {String s "<License><Data><Products><Product>Aspose.Total for Java</Product><Product>Aspose.Wo…...
生信技能45 - 基于docker容器运行生信软件
1. 获取docker镜像 以运行xhmm CNV分析软件为例。 # 搜索仓库镜像 sudo docker search xhmm# 拉取镜像 sudo docker pull ksarathbabu/xhmm_v1.0# 启动镜像,非后台 sudo docker run -it ksarathbabu/xhmm_v1.0 /bin/bash # -i: 交互式操作。 # -t: 终端。 # ksarathbabu/xhmm…...

算法训练营第63天|LeetCode 84.柱状图中最大的矩形
完结!撒花! LeetCode 84.柱状图中最大的矩形 题目链接: LeetCode 84.柱状图中最大的矩形 代码: class Solution { public:int largestRectangleArea(vector<int>& heights) {heights.insert(heights.begin(),0);he…...

python跟C++选哪个?
选择使用Python还是C取决于你的具体需求和项目背景。我这里有一套编程入门教程,不仅包含了详细的视频讲解,项目实战。如果你渴望学习编程,不妨点个关注,给个评论222,私信22,我在后台发给你。 在通信工程行业…...

速锐得深入解析吉利几何CAN总线数据通信网络的拓扑层级框架技术
在现代汽车工业中,车辆的电子控制单元(ECU)之间的通信至关重要。这种通信大多通过控制器局域网络(CAN)总线实现,它是德国BOSCH公司于20世纪80年代初开发的一种串行数据通信协议。随着技术的不断进步&#x…...

数据分析的数据模型
数据分析的数据模型 前言一、优化模型1.1线性优化模型1.1.1线性优化模型定义1.1.2线性优化模型求解算法1. 1.2.1图解法1. 1.2.2. 单纯形法 1.1.3 线性优化模型的应用 1.2非线性优化模型1.2.1非线性优化模型定义1.2.2非线性优化划模型求解方法1. 2.2.1有约束非线性模型算法1.2.2…...

SQL注入-通达OA SQL注入漏洞【CVE-2023-4166】原理及检测思路分析
1、漏洞描述 通达OA中发现一个漏洞,并被列为严重漏洞。该漏洞影响文件general/system/seal_manage/dianju/delete_log.php的未知代码。对参数 DELETE_STR 的操作会导致 sql 注入。 2、影响范围 通达OA版本11.10之前 3、复现环境 FOFA搜索:app"TDX…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
