神经网络有哪些算法
神经网络算法是人工智能领域的重要组成部分,它通过模拟人类神经系统的结构和功能,实现对复杂问题的处理和分析。以下是对神经网络算法的详细概述,包括常见的算法和它们的特点、应用等,力求达到约2500字的篇幅。
一、神经网络算法概述
神经网络算法是一种基于人工神经元的概念,通过模拟神经元之间的连接和信息传递来实现数据处理和决策的数学模型。它由大量简单的神经元单元组成,这些神经元单元通过相互连接来模拟信息传递和处理。神经网络算法具有自学习、自组织、自适应等特性,能够处理复杂的非线性问题,因此在模式识别、数据挖掘、图像处理等领域有着广泛的应用。
二、常见的神经网络算法
- 前馈神经网络算法(Feedforward Neural Network, FNN)
前馈神经网络算法是最基本的神经网络算法之一,其结构主要由输入层、隐藏层和输出层组成。在前馈神经网络中,信息从输入层经过隐藏层流向输出层,没有反馈连接。前馈神经网络算法通过反向传播算法进行训练,不断调整神经元之间的连接权重,以最小化预测输出与目标输出之间的差距。前馈神经网络算法适用于各种分类和回归问题,如图像识别、语音识别等。
- 卷积神经网络算法(Convolutional Neural Network, CNN)
卷积神经网络算法是一种专门用于处理图像和视频的神经网络算法。它模拟了人类视觉处理信息的方式,能够识别出不同方向、大小、颜色和形状的图像模式。卷积神经网络算法主要由卷积层、池化层和全连接层组成。其中,卷积层负责提取图像中的局部特征,池化层则对特征进行降维和抽象,全连接层则负责将特征映射到输出空间。卷积神经网络算法在图像分类、目标检测、图像生成等领域有着广泛的应用。
- 循环神经网络算法(Recurrent Neural Netw
相关文章:

神经网络有哪些算法
神经网络算法是人工智能领域的重要组成部分,它通过模拟人类神经系统的结构和功能,实现对复杂问题的处理和分析。以下是对神经网络算法的详细概述,包括常见的算法和它们的特点、应用等,力求达到约2500字的篇幅。 一、神经网络算法概述 神经网络算法是一种基于人工神经元的…...

计算机网络期末试题
第一章 概述 一. 单选题(共13题,36.4分) 1. (单选题) 因特网起源于( )网络。 A. ARPANETB. EthernetC. CATVD. CERNET 我的答案: A:ARPANET;正确答案: A:ARPANET; 2.8分 2. (单选题)人们把( )年作为因特网的诞…...

Unity学习笔记---图层
渲染层级 1,调整Sprite Renderer中的Order in Layer可以调整图层层级。 2,在Edit--Project Setting--Graphics中,调整TransParency Sort Mode为Custom Axis, 并将TransParency Sort Axis中的Z值默认的1改为0,将Y改为…...

【简单探索微软Edge】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

YOLOv5独家改进:backbone改进 | 微软新作StarNet:超强轻量级Backbone | CVPR 2024
💡💡💡创新点:star operation(元素乘法)在无需加宽网络下,将输入映射到高维非线性特征空间的能力,这就是StarNet的核心创新,在紧凑的网络结构和较低的能耗下展示了令人印象深刻的性能和低延迟 💡💡💡如何跟YOLOv5结合:替代YOLOv5的backbone 收录 YOL…...

概率密度函数pdf的某种解释与洞察
1.一个想法实验 我在想一个数,姑且称之为X,介于0和10之间(含0和10)。如果我不告诉你别的,你会想象X = 0的概率是多少?X = 4?假设我对任何特定的数字都没有偏好,你会想象十一个整数0,1,2,.….,10也是一样。因为所有的概率加起来必须是1,所以逻辑上的结论是给11个选项…...
)
【OceanBase诊断调优】—— 转储错误(错误代码 4138/ORA-01555)
当读事务很长时,租户进行转储会报 4138/ORA-01555 错误。本文介绍该错误的处理方法。 适用版本 OceanBase 数据库 V2.X 及以后的版本 问题现象 当读事务很长,租户进行转储时会出现以下错误。 Oracle 租户: ORA-01555:snapsho…...

Python面试题【数据结构和算法部分101-130】
Python面试题【数据结构和算法部分101-130】 Python面试题【数据结构和算法部分101-130】 Python面试题【数据结构和算法部分101-130】 问题:如何在Python中实现二分查找? 答案: def binary_search(arr, target):low, high 0, len(arr) - 1…...

Django中的日志处理
日志处理 1.日志级别 级别(Level)表示日志消息的优先级,从低到高分为以下几个级别: DEBUG: 详细的日志信息,通常用于调试。 INFO: 一般的信息性消息,用于说明程序运行情况。 WARNING: 警告消息࿰…...

FonePaw Data Recovery for Mac:轻松恢复丢失数据
FonePaw Data Recovery for Mac是一款功能强大的数据恢复软件,专为Mac用户设计,帮助用户轻松恢复因各种原因丢失的数据。该软件支持从硬盘驱动器、存储卡、闪存驱动器等存储介质中恢复丢失或删除的文件,包括照片、视频、文档、电子邮件、音频…...

C语言易错提醒选择题精选
Ⅰ 易错题 1.设有double p;,为变量p声明一个引用名称rp,则定义语句为 double& rpp; 2.已知‘A’一‘Z’的ASCII码为65—90,当执行“char ch14*52;cout<<ch<<endl;”语句序列后得到的输出结H ,72对应ASCII码中…...

Android11系统去掉截屏功能
1. 去掉Settings里截屏菜单条目,packages/apps/Settings: diff --git a/res/xml/top_level_settings.xml b/res/xml/top_level_settings.xml old mode 100644 new mode 100755 index a5e4d06..a9420bb --- a/res/xml/top_level_settings.xmlb/res/xml/t…...

测试驱动来学习 Promise
基础功能 测试案例:以同步的方式调用。 /*** v1: 基础功能*/ const p1 new MyPromise((resolve, reject) > {resolve(success)reject(error) })p1.then((value) > {console.log(v1: , value) }) 实现功能:在 status 和 value 的位置暂存值&…...
Vue3实战笔记(20)—封装头部导航组件
文章目录 前言一、封装头部导航栏二、使用步骤总结 前言 Vue 3 封装头部导航栏有助于提高代码复用性、统一风格、降低维护成本、提高可配置性和模块化程度,同时还可以实现动态渲染等功能,有利于项目开发和维护。 一、封装头部导航栏 封装头部导航栏&am…...
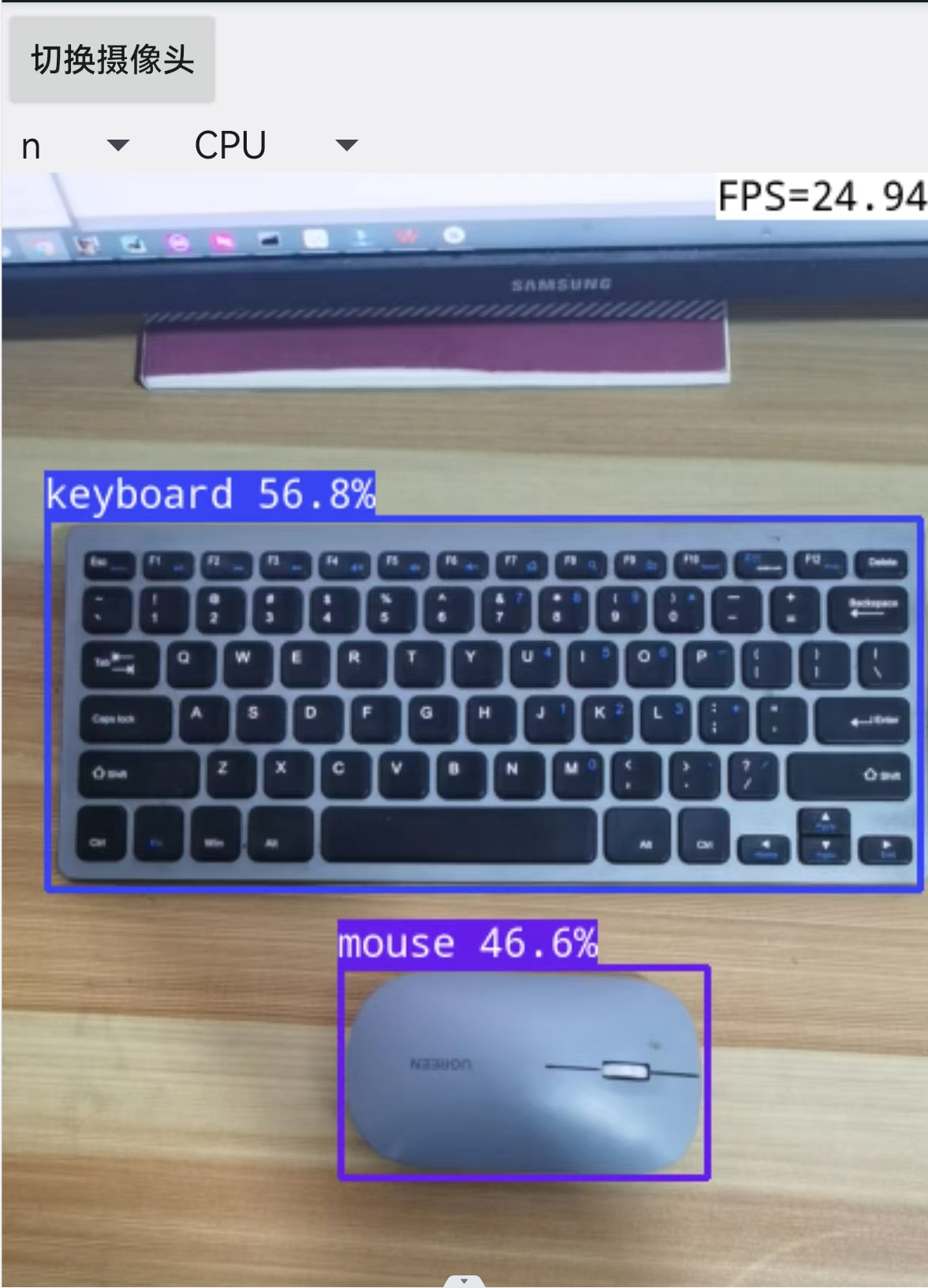
Yolov8目标检测——在Android上部署Yolov8 tflite模型
1. 简介 YOLOv8 是一种用于目标检测的深度学习模型,它是 YOLO(You Only Look Once)系列的最新版本之一。YOLO 系列因其高效和准确性而在计算机视觉领域非常受欢迎,特别是在需要实时目标检测的应用中,如视频监控、自动…...
 Object Pascal 学习笔记---第12章操作类(类方法和类数据))
(delphi11最新学习资料) Object Pascal 学习笔记---第12章操作类(类方法和类数据)
第12章 操作类 在过去的几章中,你已经了解了 Object Pascal 语言面向对象的基础:类、对象、方法、构造函数、继承、后期绑定、接口等等。现在,我们需要进一步了解与类管理相关的一些更高级、更具体的语言特性。从类引用到类助手(class he…...
面向 C# 开发人员的电子邮件转换控件 - EML 到 PNG
本文将使 C# 开发人员能够以编程方式将EML或MSG转换为其他流行的文件格式。Aspose.Email 提供了类和方法以及在线 电子邮件转换器工具,可将 EML无缝转换为PNG 。如果不安装第三方软件,则无法打开 EML/MSG 文件。因此,将 EML/MSG 转换为 PNG 和…...

Vue3:数据交互axios
回调函数 > 回调函数: 一些特殊的函数,表示未来才会执行的一些功能,后续代码不会等待该函数执行完毕就开始执行了 1. Promise 1.1 简介 > 前端中的异步编程技术,类似Java中的多线程线程结果回调! * Promise 是异步编程的一种解决方案,…...

芯片的性能指什么
【省带宽、压成本专题】降低30%视频码率,深挖“窄带高清”的实现原理 - 知乎 芯片(或微处理器、集成电路)的性能主要指其完成特定任务的能力和效率。性能可以通过多种参数来衡量,这些参数反映了芯片设计的不同方面,包…...
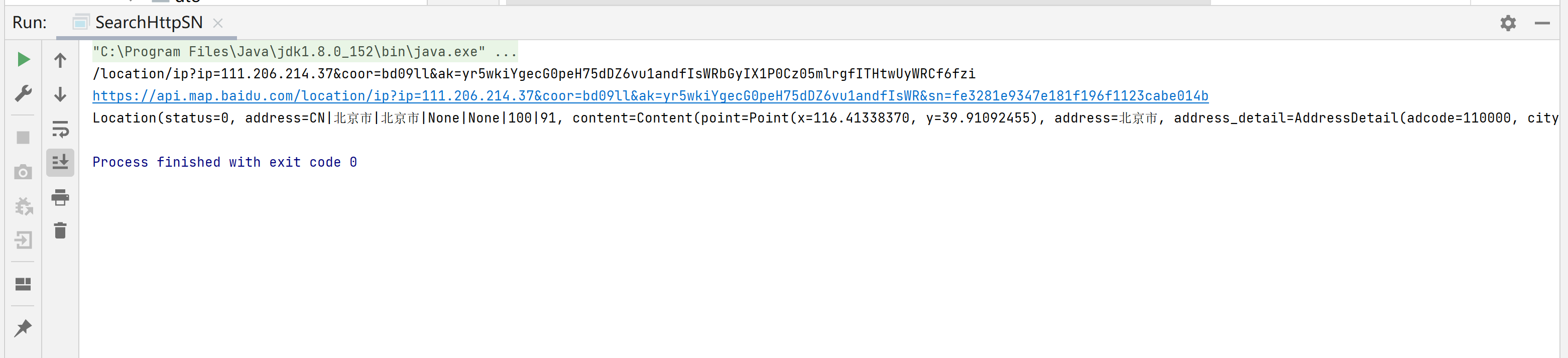
Java通过百度地图API获取定位-普通IP定位
项目中有一个登录邮箱提醒的功能,需要根据IP地址获取定位信息,从而更好地提示用户账号登录的所在地。为此,花费了一些时间来实现这个功能。 在CSDN搜索了一下,发现关于获取定位的文章说明都不够详细,于是决定自己创作一…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
