C++数据结构——红黑树
前言:本篇文章我们继续来分享C++中的另一个复杂数据结构——红黑树。
目录
一.红黑树概念
二.红黑树性质
三.红黑树实现
1.基本框架
2.插入
3.判断平衡
四.完整代码
总结
一.红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。

二.红黑树性质
-
每个结点不是红色就是黑色
-
根节点是黑色的
-
如果一个节点是红色的,则它的两个孩子结点是黑色的(不存在连续的红色节点)
-
对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点(每条路径都存在相同数量的黑色节点)
-
每个叶子结点都是黑色的(此处的叶子结点指的是空结点NULL)
如何理解红黑树最长路径不超过最短路径的二倍呢???
- 从性质能够看出,红黑树每一条路径上,都有相同数量的黑色节点。
- 红黑树每条路径上可以存在连续的黑色节点,但不能存在连续的红色节点。
- 所以最短路径即为全是黑色节点的路径。
- 最长路径则为一黑一红相间的路径。
三.红黑树实现
1.基本框架
红黑树与AVL树相比,多了节点颜色这一信息,为了实现这一信息,我们使用枚举:
enum Colour
{RED,BLACK
};template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv),_col(RED){}
};
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:private:Node* _root = nullptr;size_t _size = 0;
};同时我们多创建一个_size成员变量,用于记录节点数量。
2.插入
红黑树插入的基本步骤与二叉搜索树和AVL树一样,都是按照左子节点比根节点小,右子节点比根节点大的规则,唯一不同的是,红黑树的插入要考虑其性质。其中最值得注意的性质为:
- 不存在连续的红节点
- 每条路径上的黑节点数相等
其中能够看出,第二条才是最关键的,因此我们每次新插入节点时,必须插入红节点。
此时我们会面临两种情况:
- 父节点为黑色,插入即结束,无需调整。
- 父节点为红色,不满足上述性质1,需要调整。
下面我们来看特殊情况:
父亲为红节点,那么只有将父节点变为黑色节点,才能够满足性质。
但是如果父亲变为黑节点,就说明该路径上同样多出一个黑节点,而唯一的处理手段,就是让父亲的父亲,也就是爷爷节点,变为红色节点。
此时又存在问题,那就是关于父亲的兄弟节点,也就是叔叔节点,那么叔叔节点存在三种情况:
- 叔叔节点同样为红色。
- 叔叔节点不存在。
- 叔叔节点为黑色。
如果叔叔节点为红色,为了满足各路径黑节点数量相同,叔叔节点则需要和父节点一起变为黑色。
如果叔叔节点不存在,为了满足性质,需要将该子树从爷爷节点的位置进行旋转。
如果叔叔节点为黑色,而父节点为红色,如果还要满足性质,说明子节点原本应为黑色,是因为经过了上述的调整而作为爷爷节点变成了红色。此时我们仍需从爷爷节点的位置进行旋转。
分析完上述完整情况之后,还有关于新插入节点的两种情况:
- 父节点为爷爷节点的左子节点,同时新增节点也为父节点的左子节点,为一条斜线。
- 父节点为爷爷节点的左子节点,但是新增节点也为父节点的有子节点,为一条折线。
斜线情况下,我们在需要旋转时只需单旋即可;
而当为折线时,就需要进行双旋,先变为斜线,在进行调整。
同时父节点也需要考虑是爷爷节点的左节点还是右节点两种情况,彼此的规则相反。
按照上边的步骤,我们能够得出代码情况:
//插入bool Insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根给黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//新增节点给红色if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//parent是黑色就结束while (parent && parent->_col == RED){Node* Grandfather = parent->_parent;if (parent == Grandfather->_left){Node* uncle = Grandfather->_right;if (uncle && uncle->_col == RED)//叔叔存在且为红,直接变色{parent->_col = BLACK;uncle->_col = BLACK;Grandfather->_col = RED;//继续往上处理cur = Grandfather;parent = Grandfather->_parent;}else//叔叔不存在或叔叔存在但为黑{if (cur == parent->_left)//左边直接右旋{RotateR(Grandfather);parent->_col = BLACK;Grandfather->_col = RED;}else//右边则左右双旋{RotateL(parent);RotateR(Grandfather);cur->_col = BLACK;Grandfather->_col = RED;}break;}}else{Node* uncle = Grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;Grandfather->_col = RED;cur = Grandfather;parent = Grandfather->_parent;}else{if (cur == parent->_right){RotateL(Grandfather);Grandfather->_col = RED;parent->_col = BLACK;}else{RotateR(parent);RotateL(Grandfather);cur->_col = BLACK;Grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}需要考虑的情况确实很多,但如果自己画图认真分析,理解起来还是易如反掌的。
3.判断平衡
判断红黑树的平衡,我们自然要从其性质入手:
- 首先就是判断根节点是否为黑色。
- 其次容易判断的是是否有两个相邻的红色节点,注意这里我们不去判断一个节点与其子节点,反而去判断一个节点与其父节点。因为如果判断子节点,则可能需要判断两次,而父节点则只需判断一次。
- 最后就是判断所有路径上的黑节点数量是否相同。
其中前两种都比较容易想到代码方式,最重要的是如何比较黑节点的数量。
我们可以通过增加参数的方式。来记录到达每个节点位置时,该路径上出现过的黑节点的数量。而如何进行比较,因为每条路径上黑节点的数量都必须相同,所以我们直接记录一下最左边的一条路径上黑节点的数量,然后求出一条路径上的黑节点数之后,就进行比较即可。
//判断平衡bool IsBalance(){if (_root->_col == RED)return false;int refnum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)refnum++;cur = cur->_left;}return Check(_root, 0, refnum);}bool Check(Node* root, int BlackNum,const int refnum){if (root == nullptr){if (refnum != BlackNum){cout << "存在黑色节点个数不相等" << endl;return false;}cout << BlackNum << endl;return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "->存在连续的红色节点" << endl;return false;}if (root->_col == BLACK)BlackNum++;return Check(root->_left, BlackNum,refnum)&& Check(root->_right, BlackNum,refnum);}四.完整代码
enum Colour
{RED,BLACK
};template<class K,class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv),_col(RED){}
};
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://插入bool Insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根给黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//新增节点给红色if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//parent是黑色就结束while (parent && parent->_col == RED){Node* Grandfather = parent->_parent;if (parent == Grandfather->_left){Node* uncle = Grandfather->_right;if (uncle && uncle->_col == RED)//叔叔存在且为红,直接变色{parent->_col = BLACK;uncle->_col = BLACK;Grandfather->_col = RED;//继续往上处理cur = Grandfather;parent = Grandfather->_parent;}else//叔叔不存在或叔叔存在但为黑{if (cur == parent->_left)//左边直接右旋{RotateR(Grandfather);parent->_col = BLACK;Grandfather->_col = RED;}else//右边则左右双旋{RotateL(parent);RotateR(Grandfather);cur->_col = BLACK;Grandfather->_col = RED;}break;}}else{Node* uncle = Grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;Grandfather->_col = RED;cur = Grandfather;parent = Grandfather->_parent;}else{if (cur == parent->_right){RotateL(Grandfather);Grandfather->_col = RED;parent->_col = BLACK;}else{RotateR(parent);RotateL(Grandfather);cur->_col = BLACK;Grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}//右单旋void RotateR(Node* parent){//定义左子节点Node* subL = parent->_left;//定义左子节点的右子节点Node* subLR = subL->_right;//调整parent->_left = subLR;//判空if (subLR)subLR->_parent = parent;//调整subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root)//判断是否为根{_root = subL;_root->_parent = nullptr;}else//不是根节点,调整父节点指向{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}}//左单旋void RotateL(Node* parent){//定义右子节点Node* subR = parent->_right;//定义右子节点的左子节点Node* subRL = subR->_left;//调整parent->_right = subRL;//判空if (subRL)subRL->_parent = parent;//调整subR->_left = parent;Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root)//判断是否为根{_root = subR;_root->_parent = nullptr;}else//不是根节点,调整父节点指向{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}}//遍历void InOrder(){inOrder(_root);cout << endl;}void inOrder(const Node* root){if (root == nullptr){return;}inOrder(root->_left);cout << root->_kv.first << ':' << root->_kv.second << endl;inOrder(root->_right);}//判断平衡bool IsBalance(){if (_root->_col == RED)return false;int refnum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)refnum++;cur = cur->_left;}return Check(_root, 0, refnum);}bool Check(Node* root, int BlackNum,const int refnum){if (root == nullptr){if (refnum != BlackNum){cout << "存在黑色节点个数不相等" << endl;return false;}cout << BlackNum << endl;return true;}if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "->存在连续的红色节点" << endl;return false;}if (root->_col == BLACK)BlackNum++;return Check(root->_left, BlackNum,refnum)&& Check(root->_right, BlackNum,refnum);}
private:Node* _root = nullptr;//size_t _size = 0;
};总结
关于红黑树的知识就分享这么多,喜欢本篇文章记得一键三连,我们下期再见!
相关文章:

C++数据结构——红黑树
前言:本篇文章我们继续来分享C中的另一个复杂数据结构——红黑树。 目录 一.红黑树概念 二.红黑树性质 三.红黑树实现 1.基本框架 2.插入 3.判断平衡 四.完整代码 总结 一.红黑树概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个…...

Java并发编程:学习路线图
文章目录 一、操作系统内核原理1、进程管理详解2、内存管理详解3、IO输入输出系统详解4、进程间通信机制详解5、网络通信原理剖析 二、Java内存模型三、并发集合1、Map(1)ConcurrentHashMap(2)ConcurrentSkipListMap 2、List&…...

算法_前缀和
DP34 【模板】前缀和 import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别int n in.nextInt(),q in.ne…...
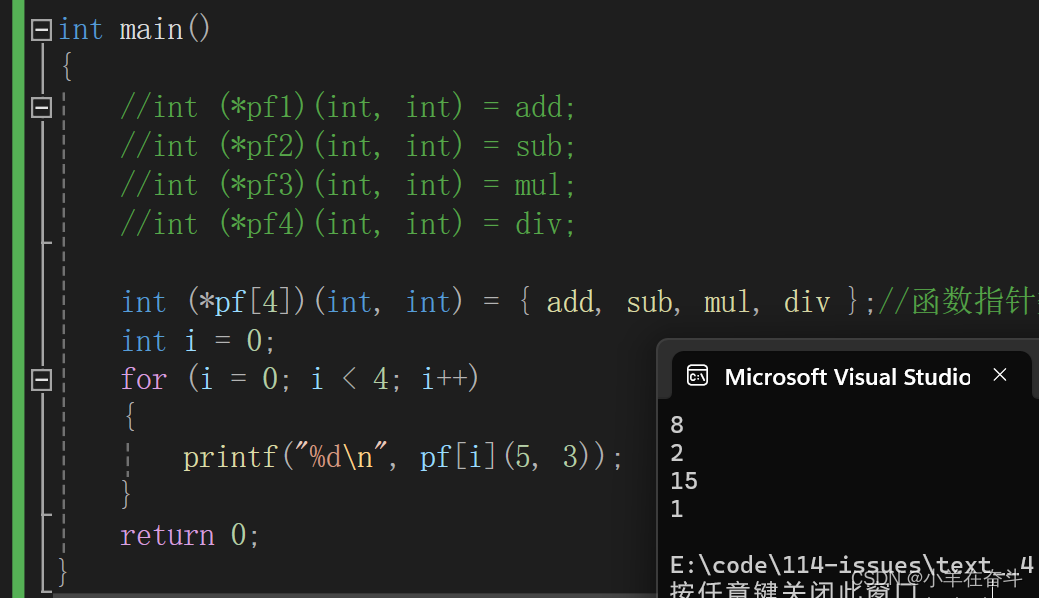
C语言(指针)7
Hi~!这里是奋斗的小羊,很荣幸各位能阅读我的文章,诚请评论指点,关注收藏,欢迎欢迎~~ 💥个人主页:小羊在奋斗 💥所属专栏:C语言 本系列文章为个人学习笔记&#x…...

线程纵横:C++并发编程的深度解析与实践
hello !大家好呀! 欢迎大家来到我的Linux高性能服务器编程系列之《线程纵横:C并发编程的深度解析与实践》,在这篇文章中,你将会学习到C新特性,并发编程,以及其如何带来的高性能的魅力࿰…...

在阿里云服务器上安装MySQL
目录 一、先卸载不需要的环境 1.关闭MySQL服务 2.查看安装包以及卸载安装包 3.依次卸载所有包 4. 获取mysql官⽅yum源 二、安装(密钥过期解决方法) 三、启动并进入 关于MySQL MySQL是一个广泛使用的开源关系型数据库管理系统(RDBMS&…...
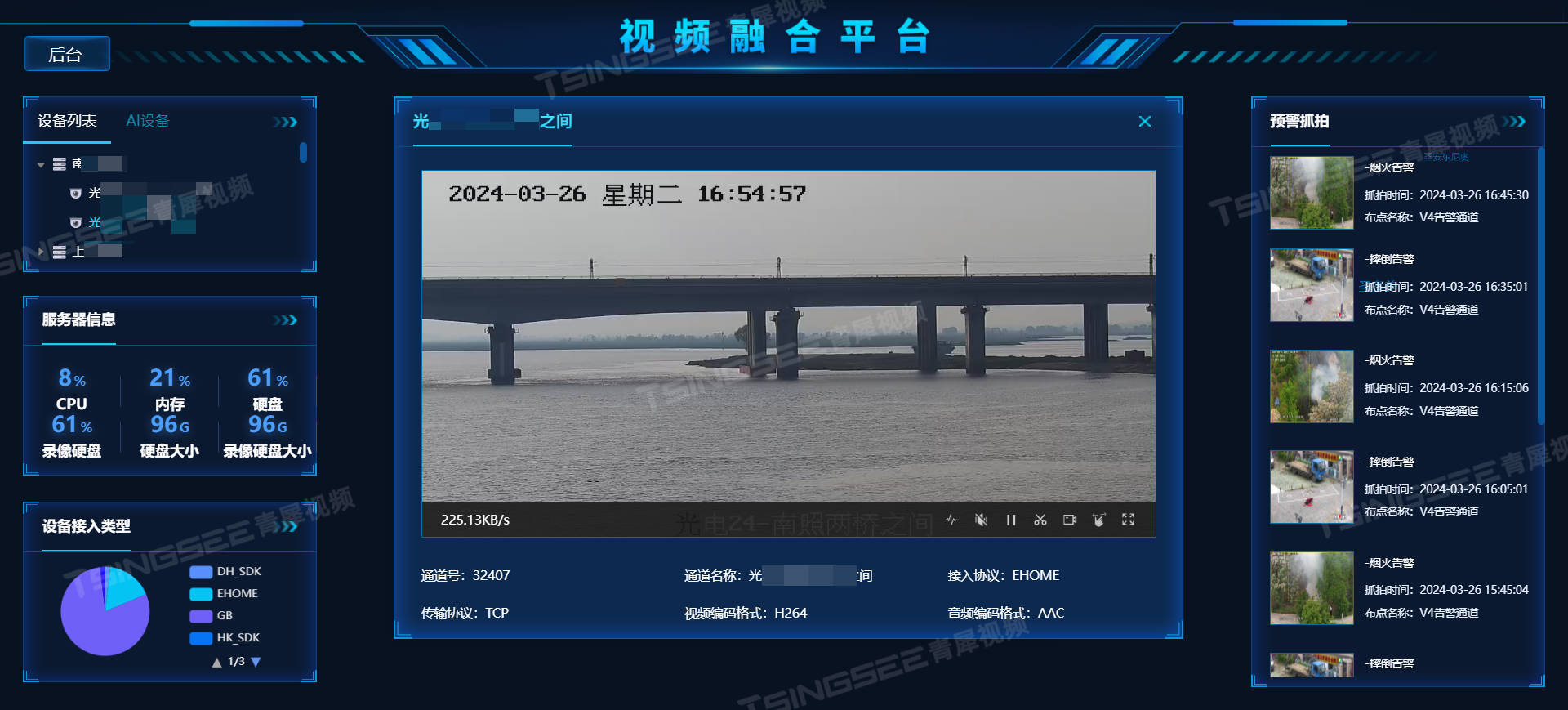
国标GB28181协议EasyCVR视频汇聚平台获取设备录像仅展示部分片段的原因排查
国标GB28181协议EasyCVR安防平台可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级联、磁盘阵列存储、视频集中存储、云存储等丰富的视频能力,平台支持7*24小时实时高清视频监控,能同时播放多路监控视频流…...
Java的类和对象(一)—— 初始类和对象,this关键字,构造方法
前言 从这篇文章开始,我们就进入到了JavaSE的核心部分。这篇文章是Java类和对象的第一篇,主要介绍类和对象的概念,this关键字以及构造方法~~ 什么是类?什么是对象? 学过C语言的老铁们,可以类比struct自定义…...

富格林:曝光虚假套路规避亏损
富格林指出,在现货黄金市场中,交易时间很充足投资机会也多的是,但为什么还是有人亏损甚至爆仓呢?其实导致这种情况,是因为有一些投资者不知道其中的虚假套路,很容易就一头栽进去了。要规避虚假套路带来的亏…...

数据源网站分享
1. 国家统计局: http://www.stats.gov.cn/提供国家宏观经济数据 2. 工业和信息化部: http://www.miit.gov.cn 发布工业运行及信息化相关数据 3. 中国人民银行: http://www.pbc.gov.cn/ 提供金融市场政策及运行相关数据 4. 国家金融监督…...

Flutter 中的 CupertinoAlertDialog 小部件:全面指南
Flutter 中的 CupertinoAlertDialog 小部件:全面指南 在Flutter中,CupertinoAlertDialog是用于在iOS风格的应用中显示警告或提示信息的模态对话框。它以其圆角卡片和模糊背景为特点,为用户提供了一个简洁而直观的交互界面。CupertinoAlertDi…...
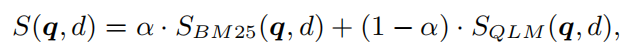
【RAG 论文】UPR:使用 LLM 来做检索后的 re-rank
论文:Improving Passage Retrieval with Zero-Shot Question Generation ⭐⭐⭐⭐ EMNLP 2022, arXiv:2204.07496 Code: github.com/DevSinghSachan/unsupervised-passage-reranking 论文:Open-source Large Language Models are Strong Zero-shot Query…...
安全风险 - 如何解决 setAccessible(true) 带来的安全风险?
可能每款成熟的金融app上架前都会经过层层安全检测才能执行上架,所以我隔三差五就能看到安全检测报告中提到的问题,根据问题的不同级别,处理的优先级也有所不同,此次讲的主要是一个 “轻度问题” ,个人认为属于那种可改…...

创建继承自QObject的线程:一个详细指南
目录标题 步骤 1:创建一个新的QObject子类步骤 2:在新的QObject子类中实现工作代码步骤 3:创建一个新的QThread对象步骤 4:管理线程的生命周期步骤 5:处理线程间通信结论 在Qt中,线程可以通过继承QThread类…...

java项目之智慧图书管理系统设计与实现(springboot+vue+mysql)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的智慧图书管理系统设计与实现。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 智慧图书管理…...

分享一些人生道理,希望能对大家有所帮助!
1. 别总想出风头,炫耀就是深渊,贪心就是毁灭,人性的恶一旦被激发,后果不堪设想。 2. 戒取怨之言:不要说招人怨恨的话,播下使人怨恨的种子。 3. 学会感恩,因为感恩能够让你更加幸福。 4. 玉碎不能…...

【设计模式】JAVA Design Patterns——Abstract-document(抽象文档模式)
🔍 目的 使用动态属性,并在保持类型安全的同时实现非类型化语言的灵活性。 🔍 解释 抽象文档模式使您能够处理其他非静态属性。 此模式使用特征的概念来实现类型安全,并将不同类的属性分离为一组接口 真实世界例子 考虑由多个部…...
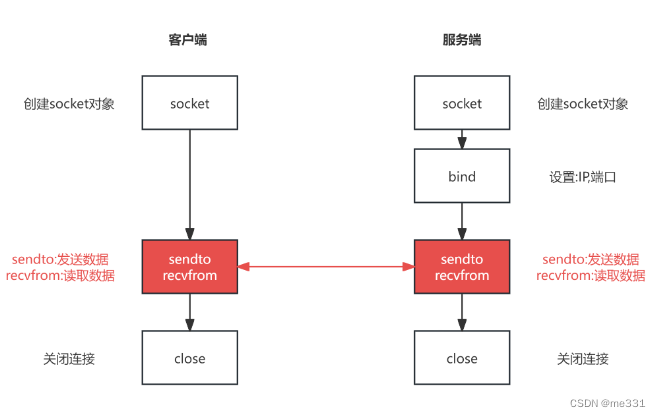
5.13网络编程
只要在一个电脑中的两个进程之间可以通过网络进行通信那么拥有公网ip的两个计算机的通信是一样的。但是一个局域网中的两台电脑上的虚拟机是不能进行通信的,因为这两个虚拟机在电脑中又有各自的局域网所以通信很难实现。 socket套接字是一种用于网络间进行通信的方…...

那些年使用过的UA头
一些WAF会根据扫描器UA头进行屏蔽 UA头 在sqlmap 中可以使用 –random-agnet /xx.txt 来更换UA头 Mozilla/5.0 (Windows NT 6.1; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/39.0.2171.95 Safari/537.36 OPR/26.0.1656.60 Opera/8.0 (Windows NT 5.1; U; en) Mozi…...

IT技术产品:开发者极为重要的思维习惯
1、特色内容预告 1、我用敏捷开发思维,提高工作效率。 2、我用代码批判思维,逐渐让自己的作品变得无可挑剔。 3、我是一个顶级程序员,是哪些重要的专业习惯,让我如此优秀? 2、可以免费获取到的IT资源 1、《软件工程&a…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
