算法题--华为od机试考试(组成最大数、第k个排列、最小传输时延)
目录
组成最大数
题目描述
输入描述
输出描述
示例1
输入
输出
示例2
输入
输出
解析
答案
第k个排列
题目描述
输入描述
输出描述
示例1
输入
输出
示例2
输入
输出
解析
答案
最小传输时延
题目描述
输入描述
输出描述
示例1
输入
输出
解析
答案
组成最大数
考察排序
题目描述
小组中每位都有一张卡片,卡片上是6位内的正整数,将卡片连起来回以组成多种数字。
输入描述
","号分割的多个正整数字符串,不需要考虑非数字异常情况,小组最多25个人。
输出描述
最大的数字字符串
示例1
输入
22,221
输出
22221
示例2
输入
22,221,35,351,356
输出
3563535122221
解析
通过逗号分割成若干个数组,高位数字越大的应该越放前面。需要考虑不同个数的数字该如何排序,例如456,43632,这种比较前三位即可出结果456排前面。
例子改为456和456457时应该谁排前面?这里可以通过循环小的位数补齐判断,456456和456457可以得出456457排前面。所以我们可以将所有的位数不够6位的循环补齐6位后再直接排序。
答案
function getMaxNumber(str) {let numArr = str.split(',')numArr = numArr.map(v => ({value: v,sortValue: v.repeat(6).slice(0, 6)}))numArr.sort((a, b) => b.sortValue - a.sortValue)return numArr.map(v => v.value).join('')
}
console.log(getMaxNumber('22,221,35,351,356'))第k个排列
考察分解问题,排列
题目描述
给定参数n,从1到n会有n个整数:1,2,3,...,n,这n个数字共有n!种排列。按大小顺序升序列出所有排列情况,并一一标记,
当n=3时,所有排列如下:
'123'
'132'
'213'
'231'
'312'
'321'
给定n和k,返回第k个排列
输入描述
输入两行,第一行为n,第二行为k,给定n的范围是[1,9],给定k的范围是[1,n!]。
输出描述
输出排在第k位置的数字。
示例1
输入
3
3
输出
213
示例2
输入
4
7
输出
2134
解析
分解问题,每次取出第一位数。最后组成结果,例如示例2,所有的排列有1***,2***,3***,4***。以1开头的一共有3!=6个数,即排1~6的都是1***的。
故直接除以6即可得到在哪个区间,余数是剩余几位数的位置。同理依次往下取下一位即可。
答案
function getPermutation(str) {let arr = str.split('\n')if (arr[0] === '1') {return 1}let num = Number(arr[0])// 剩余数let numArr = new Array(num).fill(0).map((v, i) => i + 1)let index = Number(arr[1])let res = ''while (index) {let tmp = Math.ceil(index / factorial(num - 1)) - 1// 每次取出第一位数res += numArr[tmp]numArr.splice(tmp, 1)// 剩余数的第k个位置index = index % factorial(num - 1)num--}return res + numArr[0]
}
function factorial(n) {if (n === 1) {return 1}return n * factorial(n - 1)
}console.log(getPermutation(`3
3`))
console.log(getPermutation(`4
7`))最小传输时延
考察深度遍历,递归,hash
题目描述
某通信网络中有N个网络节点,用1到N进行标识。网络通过一个有向无环图表示,其中图的边的值表示节点之间的消息传递时延。现给定相连节点之间
的时延列表times[i]={u,v,w},其中u表示源节点,v表示目的节点,w表示u和v之间的消息传递时延。请计算给定源节点到目的节点的最小传输时延,如果目的
节点不可达,返回-1。注:1.N的取值范围为[1,100];2.时延列表times的长度不超过6000,且1<=u,v<=N,0<=w<=100;
输入描述
输入的第一行为两个正整数,分别表示网络结点的个数N,以及时延列表的长度M,用空格分隔;接下来的M行为两个节点间的
时延列表[u v w];输入的最后一行为两个正整数u和v,分别表示源结点和目的结点;
输出描述
输出一个整数,表示源结点到目的结点的最小时延。
示例1
输入
3 3
1 2 11
2 3 13
1 3 50
1 3
输出
24
解析
1.将能否到达目标节点用key-value的形式表示。通过访问对象的key是否存在判断是否能到达目标节点,其中key为起点-终点,value为时延值。
2.使用深度遍历(递归)来查找是否能到达终点。
我们用f(start,end)表示start到end的最小时延,首先需要找到f(start,end)和下一次的关系。等于start能到的所有节点出发的值中最小的一个加第一次时延的最小值。
即f(start,end)=min(f(start1,end)+start-start1,f(start2,end)+start-start2,f(start3,end)+start-start3....),这里start1,start2,start3,为start能到的节点。
start-start1,表示start到start1节点的时延。
3.找终点。
1.走过的节点不能再走避免循环(通过set记录走过的节点)。
2.当前时延超过之前记录的最小时延时不需要继续往下了。
3.当start的可达节点中有end时不需要往下继续找了。
答案
function getMinTimeDelay(str) {let paramArr = str.split('\n')let [start, end] = paramArr.pop().split(' ')let hash = {}let nodeHash = {}paramArr.forEach(v => {let tmp = v.split(' ')hash[`${tmp[0]}-${tmp[1]}`] = Number(tmp[2])if (!nodeHash[tmp[0]]) {nodeHash[tmp[0]] = {next: [tmp[1]]}} else {nodeHash[tmp[0]].next.push(tmp[1])}})let res = 0let set = new Set(start)let min = findMin(start, end, res, set, nodeHash, hash)if (min) {return min}return -1
}
function findMin(start, end, res, set, nodeHash, hash, min = Infinity) {let next = nodeHash[start].next// 大于已有结果的时延,不再往下继续寻找if (res >= min) {return}let len = next.length// 深度遍历,查找每一条路径的时延for (let i = 0; i < len; i++) {let tmp = next[i]// 找到了终点if (tmp === end) {if (min > res + hash[start + '-' + end]) {min = res + hash[start + '-' + end]}continue}// 下一个结点不能为走过的节点if (!set.has(tmp)) {// 记录走过的节点set.add(tmp)let result = findMin(tmp, end, res + hash[start + '-' + tmp], set, nodeHash, hash, min)if (result < min) {min = result}// 下一次循环前还原走过的节点set.delete(tmp)}}if (min !== Infinity) {return min}return
}
console.log(getMinTimeDelay(`3 3
1 2 11
2 3 13
1 3 50
1 3`))相关文章:
)
算法题--华为od机试考试(组成最大数、第k个排列、最小传输时延)
目录 组成最大数 题目描述 输入描述 输出描述 示例1 输入 输出 示例2 输入 输出 解析 答案 第k个排列 题目描述 输入描述 输出描述 示例1 输入 输出 示例2 输入 输出 解析 答案 最小传输时延 题目描述 输入描述 输出描述 示例1 输入 输出 解析…...
2024 年最新本地、云服务器安装部署 miniconda 环境详细教程(更新中)
Anaconda 概述 Anaconda 是专门为了方便使用 Python 进行数据科学研究而建立的一组软件包,涵盖了数据科学领域常见的 Python 库,并且自带了专门用来解决软件环境依赖问题的 conda 包管理系统。主要是提供了包管理与环境管理的功能,可以很方便…...
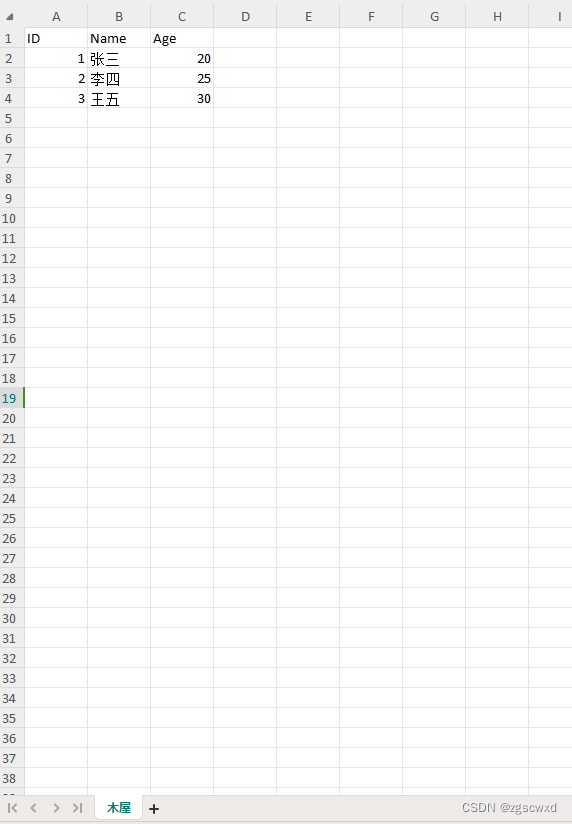
Python进行excel处理-01
最近干采购,每个月要对供应商的对账单,对对应的采购订单号和物料编号的价格和数量,是不是和物料管控总表里面的价格数量是不是一致,于是写了一个代码。 从总表里面找到,对账单里对应采购订单和物料编码的数据…...
苹果macOS无法给App麦克风授权解决办法
好久没有在电脑上录制课程了,有些东西还是录下来记忆深刻,却意外发现MAC系统升级后无法授权给第三方的App使用摄像头和麦克风,而录屏软件是需要开启麦克风和摄像头才能录制屏幕上的操作和声音,官方提示在第三方APP若有使用摄像头和…...

图的深度优先遍历
way:栈,map(或set,只是我想用map)记录是否访问过,放入时记录为已访问,打印,邻接的没访问过先入cur,再入邻接的节点,放入一个邻接的节点后及时break去下一个深…...
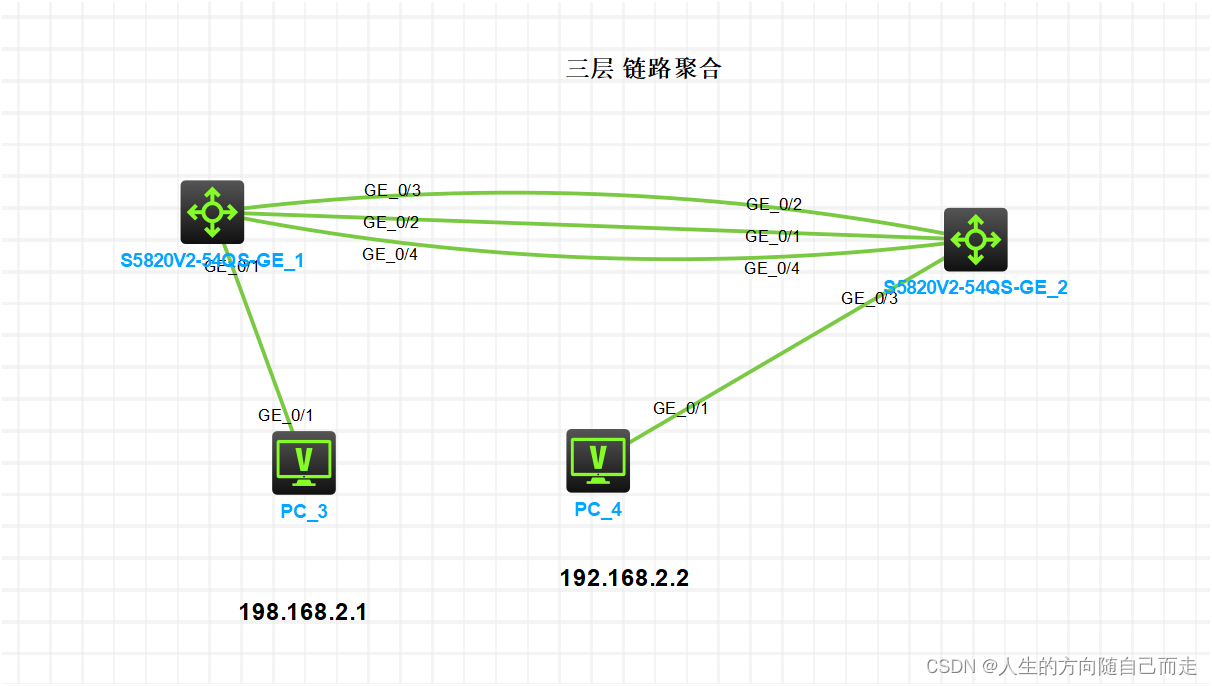
13 华三三层链路聚和
13 华三三层链路聚和 AI 解析 华三三层静态路由是指在华三交换机上配置的一种路由方式。它通过在交换机上手动配置路由表,将不同网络之间的数据进行转发。 华三三层静态路由的配置步骤如下: 1. 配置交换机接口的IP地址:在交换机上选择要配…...
C# 下载安装,使用OfficeOpenXml
下载安装OfficeOpenXml模块 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.IO; using System.Linq; using System.Reflection.Emit; using System.Text; using System.Text.RegularEx…...
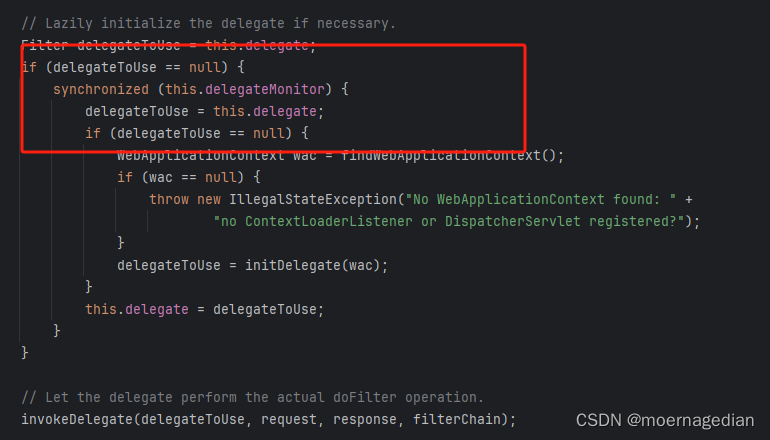
Spring整体流程源码分析
DisableEncodeUrlFilter 防止sessionId被泄露 包装器模式 WebAsyncManagerIntegrationFilter WebAsyncManagerIntegrationFilter通常与Spring MVC的异步请求处理机制一起使用,确保在使用Callable或DeferredResult等异步处理方式时,安全上下文能够正…...
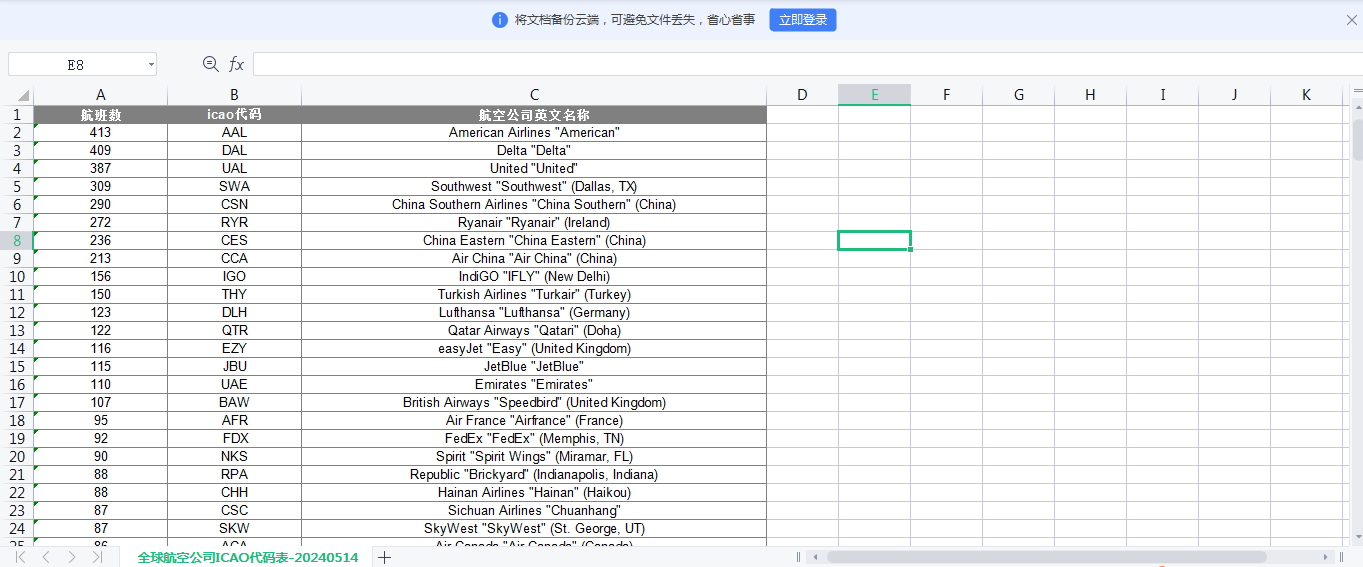
使用XxlCrawler抓取全球航空公司ICAO三字码
目录 前言 一、数据源介绍 1、目标网站 2、页面渲染结构 二、XxlCrawler信息获取 1、创建XxlCrawler对象 2、定义PageVo对象 3、直接PageVO解析 4、自定义解析 总结 前言 长距离旅行或者出差,飞机一定是出行的必备方式。对于旅行达人或者出差人员而言&…...

Java String转JSONObject时保持字段顺序不变
Java String转JSONObject时保持字段顺序不变 问题背景解决方案 问题背景 在业务接口开发过程中,有一个新增接口,需要支持批量新增数据,这时入参就需要用到 json 格式数据,且包含 list 集合,比如这样的数据格式&#x…...
Optional用法
说明:Optional和Stream一样,是Java8引入的特性,本文介绍Optional的几个实际用法。Steam流使用,参考下面这篇文章: Stream流使用 使用 1.保证值存在 // 1.保证值存在,pageNumber,pageSizeInte…...
【观成科技】加密C2框架Xiebro流量分析
一、工具介绍 Xiebro是由Golang和 .NET编写,提供支持的多人和多服务器 C2/后开发框架。它支持多种通信协议,包括TCP、websocket等,并且在客户端与Xiebro服务器之间的通信通常采用AES加密来保障安全性和隐蔽性。 二、工具原理分析 Xiebro C…...
【八大排序算法】插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序、计数排序
文章目录 一、排序的相关概念二、排序类型三、排序算法实现插入排序1.直接插入排序2.希尔排序 选择排序3.简单选择排序4.堆排序 交换排序5.冒泡排序6.快速排序递归实现非递归实现 7.归并排序递归实现非递归实现 8.计数排序 四、总结 一、排序的相关概念 排序:根据数…...

Flutter 中的 CupertinoActionSheet 小部件:全面指南
Flutter 中的 CupertinoActionSheet 小部件:全面指南 在Flutter中,CupertinoActionSheet是用于在iOS风格的应用中显示动作面板的组件。它提供了一个简洁的界面,让用户可以快速从一组选项中做出选择。CupertinoActionSheet通常伴随着一个或多…...
IDEA 好用的插件
图标插件:Atom Material Icons 此插件的作用就是更好的显示各种文件的类别,使之一目了然 汉化包 Chinese (Simplified) Language Pack / 中文语言包 作用就是 汉化 AI编码助手 GitHub Copilot AI编码助手:提示代码很好用 缺点:…...
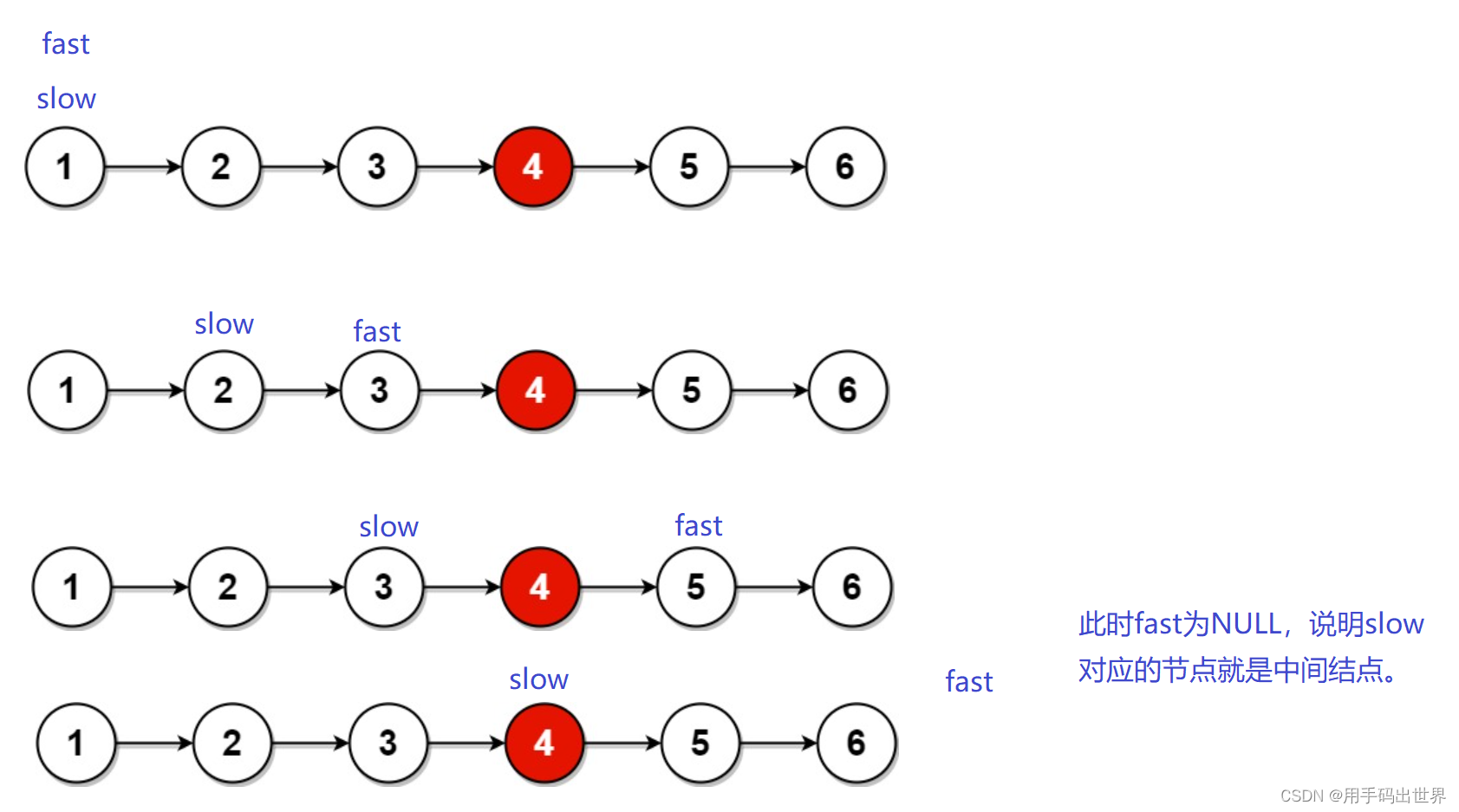
leetcode——链表的中间节点
876. 链表的中间结点 - 力扣(LeetCode) 链表的中间节点是一个简单的链表OJ。我们要返回中间节点有两种情况:节点数为奇数和节点数是偶数。如果是奇数则直接返回中间节点,如果是偶数则返回第二个中间节点。 这道题的解题思路是&a…...
稳定网络的诀窍:静态住宅代理解决方案
在数字化时代,网络稳定性对于个人和企业都至关重要。然而,由于多种因素的影响,如地理位置、网络拥堵或网络安全问题等,网络稳定性常常受到挑战。为了应对这些挑战,静态住宅代理作为一种高效且可靠的网络解决方案&#…...

VACode 创建Vue项目完整过程
一、软件下载 VSCode官网下载地址:https://code.visualstudio.com/ 二、下载开发环境 1. 安装 [Node.js](https://nodejs.org/); 2. 安装 [npm](https://www.npmjs.com/) 依赖管理工具; 注:node.js安装完后会同步安装npm,一般…...
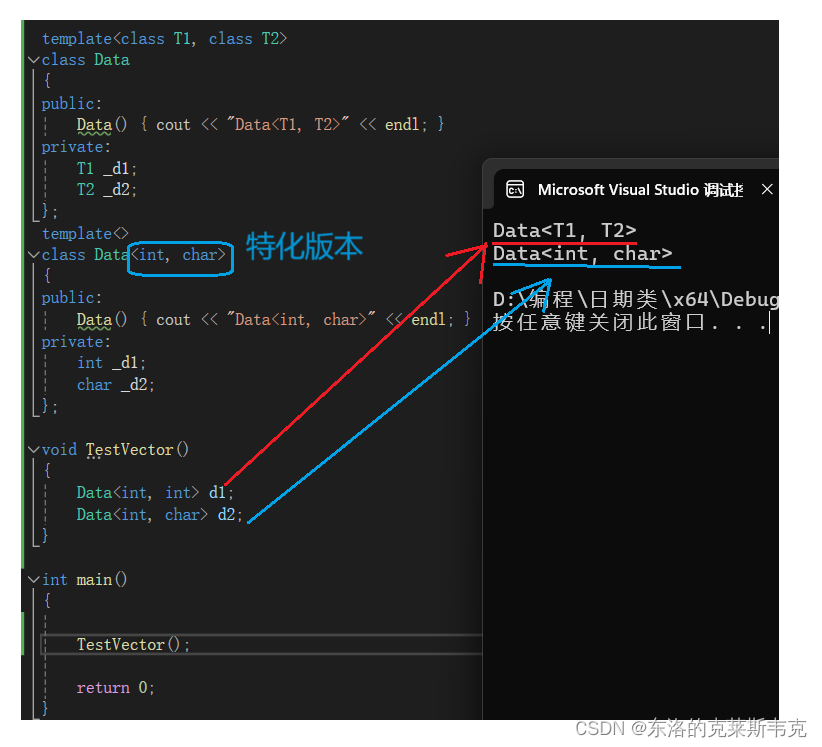
【C++】详解C++的模板
目录 概念 编辑 语法 函数模板 类模板 非类型模板参数 模板的特化 函数模板特化 类模板特化 全特化 偏特化 分离编译 概念 模板是C中非常厉害的设计,模板把通用的逻辑剥离出来,让不同的数据类型可以复用同一种模板的逻辑,甚至可以…...
1146 -Table ‘performance schema.session variables‘ doesn‘t exist的错误解决
一、问题出现 今天在本地连数据库的时候,发现这个问题,哎呦我擦,差点吓死了 二、解决办法 1)找文件 用everything搜一下MySQL Server 5.7 然后去Windows服务找一下MySQL配置文件的具体路径 如果知道那最好,不知道那…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
