LeetCode题练习与总结:不同的二叉搜索树--96
一、题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
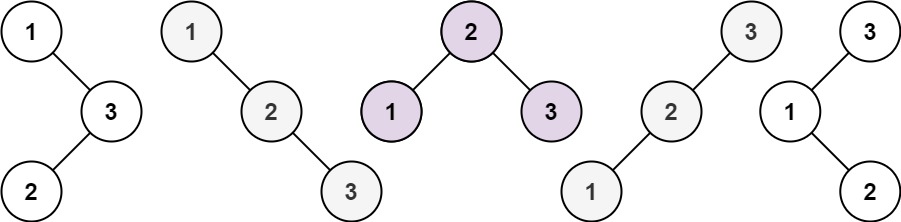
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
二、解题思路
这个问题是关于卡特兰数的经典问题。二叉搜索树(BST)的一个重要特性是,它的中序遍历结果是一个有序数组。因此,如果我们有 n 个互不相同的节点,那么可能的二叉搜索树的种数与这些节点的排列方式有关。
对于给定的 n,我们可以这样考虑:
- 选择 1 作为根节点,那么剩下的 n-1 个节点将位于根节点的右侧,可以形成 G(n-1) 种 BST。
- 选择 2 作为根节点,那么剩下的 n-2 个节点中,1 个位于根节点的左侧,n-3 个位于根节点的右侧,可以形成 G(1) * G(n-3) 种 BST。
- 以此类推,直到选择 n 作为根节点,剩下的 n-1 个节点将位于根节点的左侧,可以形成 G(n-1) 种 BST。
因此,G(n) 可以用以下公式表示:G(n)=G(0)∗G(n−1)+G(1)∗G(n−2)+...+G(n−1)∗G(0)
其中 G(0) = 1,因为只有一个节点的 BST 只有一种情况。
基于上述思路,我们可以用动态规划的方法来解决这个问题。我们可以创建一个数组 dp,其中 dp[i] 表示有 i 个节点时可能的 BST 种数。然后我们可以按照上述公式计算 dp 数组。
三、具体代码
public class Solution {public int numTrees(int n) {if (n == 0) return 1;int[] dp = new int[n+1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
}
四、时间复杂度和空间复杂度
1. 时间复杂度
- 我们有一个双重循环结构。外层循环遍历从 2 到 n 的所有整数,共执行 n - 1 次。
- 内层循环遍历从 1 到当前外层循环的整数,最坏情况下(即外层循环变量为 n 时)执行 n 次。
- 因此,内层循环总共执行次数为 1 + 2 + … + n,这是一个等差数列求和,其和为 (n * (n + 1)) / 2。
- 所以,总的时间复杂度为 O((n * (n + 1)) / 2),简化后为 O(n^2)。
2. 空间复杂度
- 我们使用了一个大小为 n+1 的数组 dp 来存储中间结果。
- 因此,空间复杂度是 O(n),即与输入大小 n 成正比。
综上所述,代码的时间复杂度是 O(n^2),空间复杂度是 O(n)。
五、总结知识点
-
动态规划(Dynamic Programming, DP):这是一种用于解决优化问题的算法思想,它将复杂问题分解为多个子问题,通过解决子问题来构建原问题的解。动态规划通常用于解决具有重叠子问题和最优子结构特性的问题。
-
二叉搜索树(Binary Search Tree, BST):这是一种特殊的二叉树,其中每个节点都满足左子树中的所有元素小于该节点的值,右子树中的所有元素大于该节点的值。题目要求计算不同结构的BST的数量。
-
卡特兰数(Catalan number):这是一个组合数学中的数列,用于计算不同结构的二叉树的数量。第 n 个卡特兰数可以通过公式 C(n) = (2n)! / ((n+1)! * n!) 计算得出,其中 n! 表示 n 的阶乘。
-
循环结构:代码中使用了两个嵌套的 for 循环,这是一种常见的控制结构,用于重复执行代码块固定的次数。
-
数组的使用:代码中使用了一个整数数组 dp 来存储中间结果,这是一种常见的数据结构,用于存储多个相同类型的数据项。
-
累加操作:在动态规划的过程中,通过累加操作计算 dp 数组的值,这是动态规划中更新状态的一种常见方式。
-
边界条件处理:代码中对于 n=0 和 n=1 的情况进行了特殊处理,这是因为在这些情况下,BST 的数量是确定的,分别为 1。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:不同的二叉搜索树--96
一、题目描述 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5示例 2: 输入:n 1 输出&…...

第八十一章 将 Web 应用程序与远程 Web 服务器结合使用 - 如果从 Web 服务器提供静态文件
文章目录 第八十一章 将 Web 应用程序与远程 Web 服务器结合使用 - 如果从 Web 服务器提供静态文件如果从 Web 服务器提供静态文件配置 Web 服务器路径将虚拟目录添加到 IIS将别名添加到 Apache 配置 第八十一章 将 Web 应用程序与远程 Web 服务器结合使用 - 如果从 Web 服务器…...
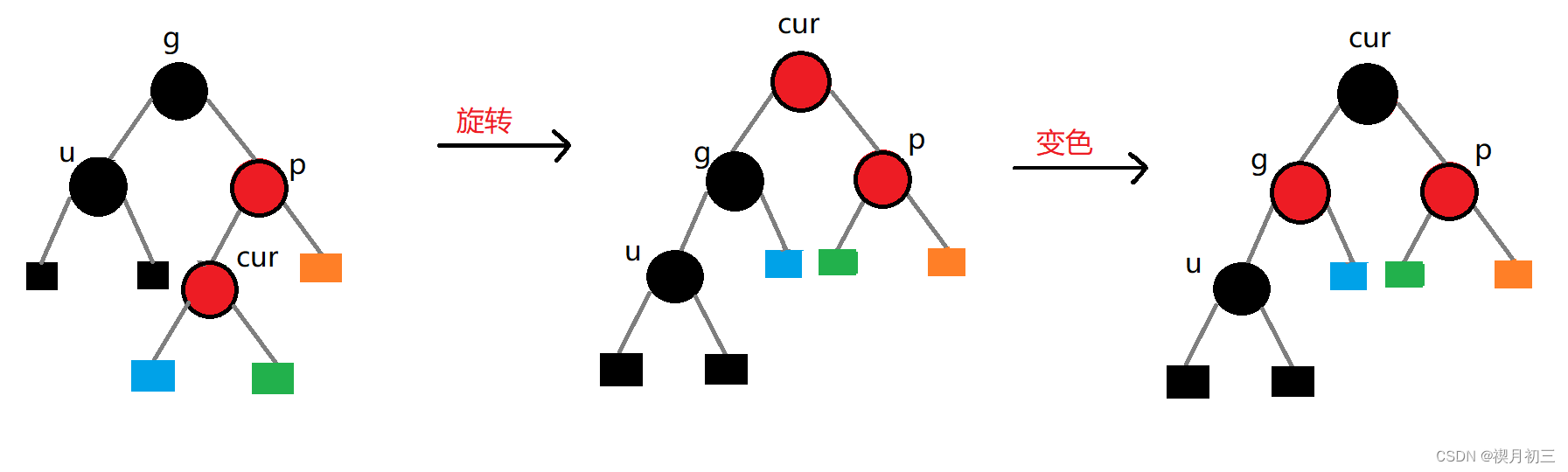
AVL树、红黑树
数据结构、算法总述:数据结构/算法 C/C-CSDN博客 AVL树 定义 空二叉树是一个 AVL 树如果 T 是一棵 AVL 树,那么其左右子树也是 AVL 树,并且 ,h 是其左右子树的高度树高为 平衡因子:右子树高度 - 左子树高度 创建节点…...
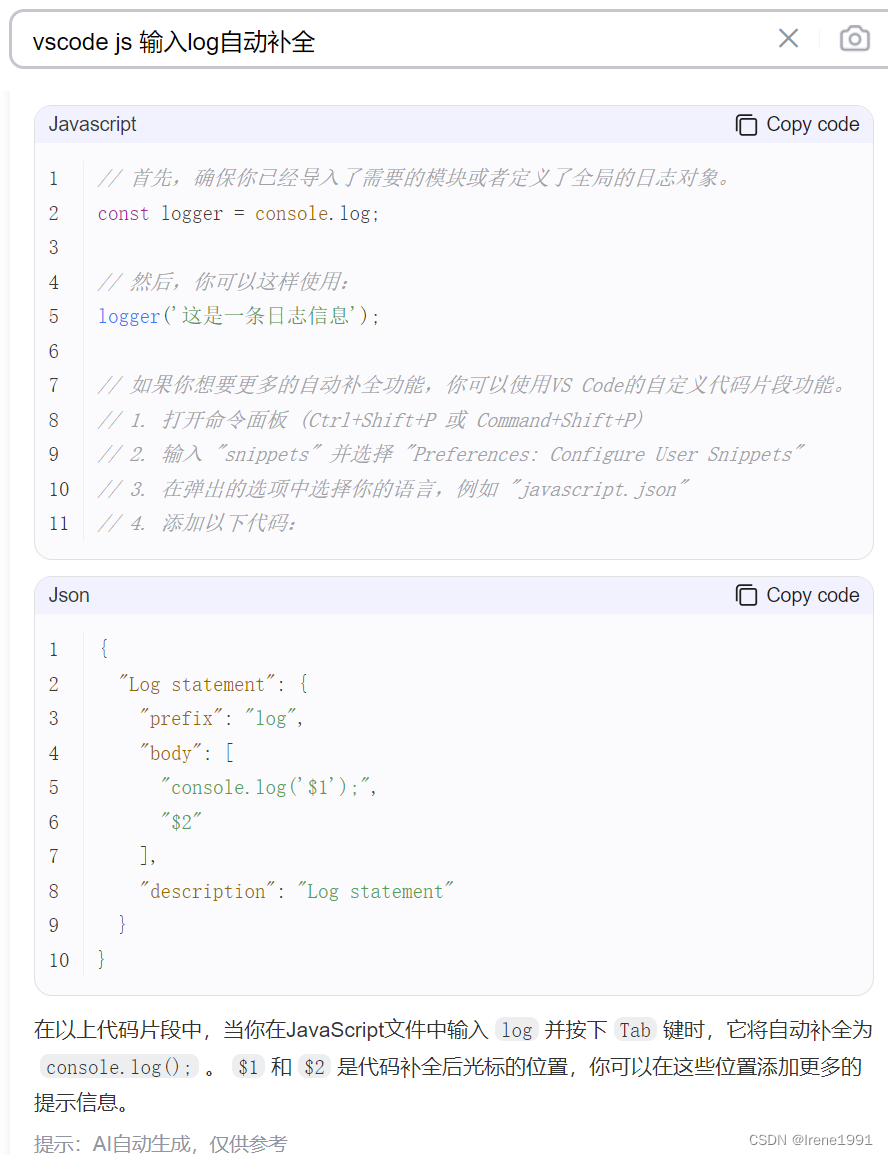
Vscode编辑器 js 输入log自动补全
最近换了新电脑,新下载了Vscode,记录一下设置项。 Vscode 版本 想要的效果 js文件中输入log(点击tab键),自动补全为 console.log() Vscode 文件》首选项》设置 搜索:snippets Emmet: Show Suggestions…...
structured concurrency
1. 基于 c executions的异步实现 - 从理论到实践 - 知乎 (zhihu.com)...

【免费】在线识别通用验证码接口
模块优势价格5元1000次,每天免费100次api文档支持 使用量小的完全够用了 <?phpfunction Post_base64($base64_str){$url http://api.95man.com:8888/api/Http/Recog?Taken41******QK&imgtype1&len0 ; $fields array( ImgBase64>$base64_str); $ch…...

如何通过汽车制造供应商协同平台,提高供应链的效率与稳定性?
汽车制造供应商协同是指在汽车制造过程中,整车制造商与其零部件供应商之间建立的一种紧密合作的关系。这种协同关系旨在优化整个供应链的效率,降低成本,提高产品质量,加快创新速度,并最终提升整个汽车产业的竞争力。以…...

使用LangChain创建简易聊天机器人
LangChain 是什么 就是一个框架或者说是一个工具,用来写 AI 应用。对,没有错!AI小白也可以,有手就行! LangChain有几个核心模块:Models、Prompts、Chains、Indexes、Memory、Agents。 这篇主要介绍Models、…...

研究生学习---找工作
规划 研一~研二上学期完成小论文,实习,秋招 竞赛:kaggle? 面试题一般简单且为原题,笔试题目很难,不会出原题 项目 找工作软件...
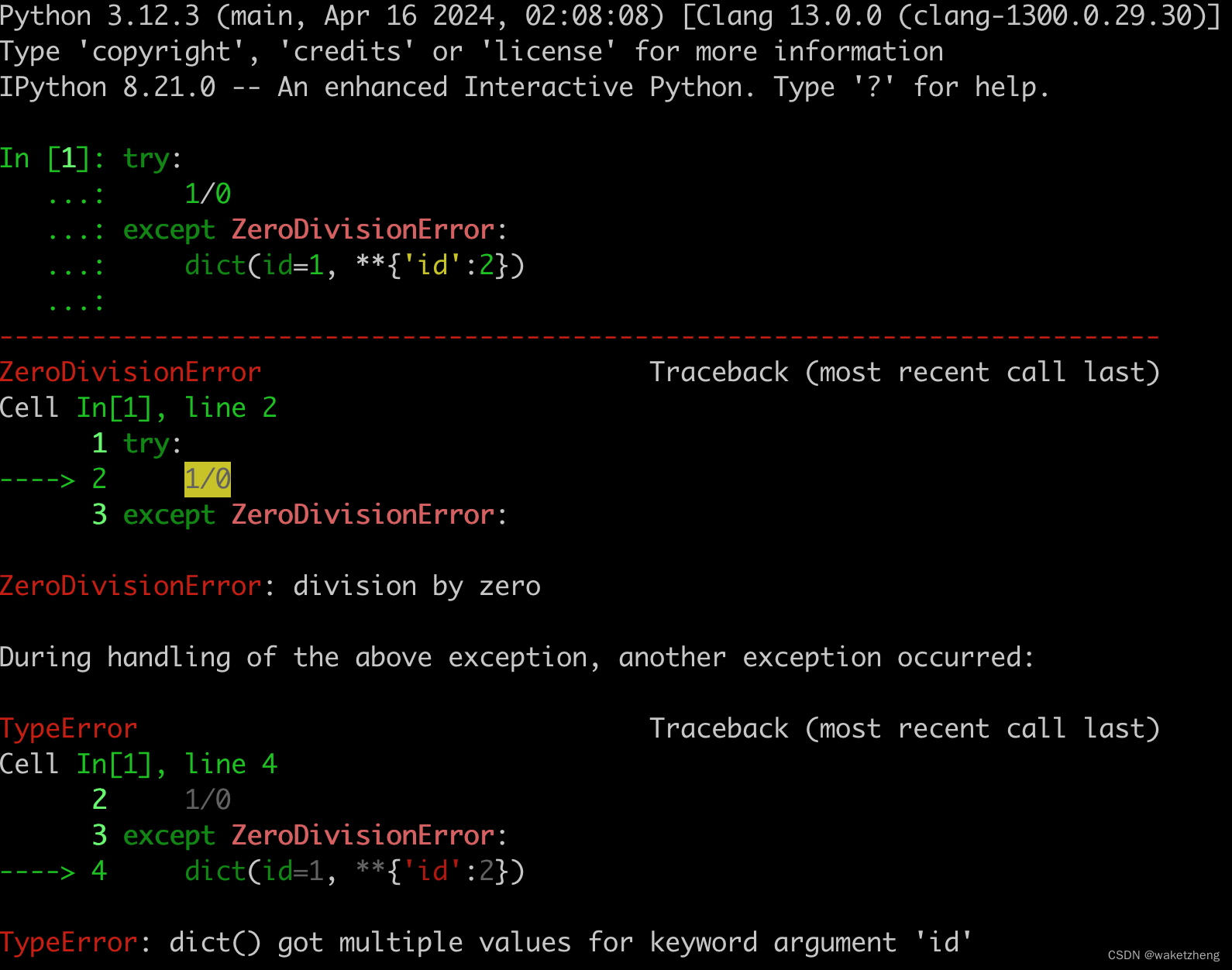
偶然发现了Python的一个BUG。。。
一般情况下,dict(id1, **{id: 1})这句代码应该报TypeError。但如果在捕获了其他异常的情况下,再来执行这句代码,却是会报KeyError,如下图: Python3.10和Python3.9也能复现该情况,正当我摩拳踩掌,…...

36. 有效的数独 - 力扣(LeetCode)
基础知识要求: Java:方法、for循环、if判断、数组 Python: 方法、for循环、if判断、列表、集合 题目: 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一…...
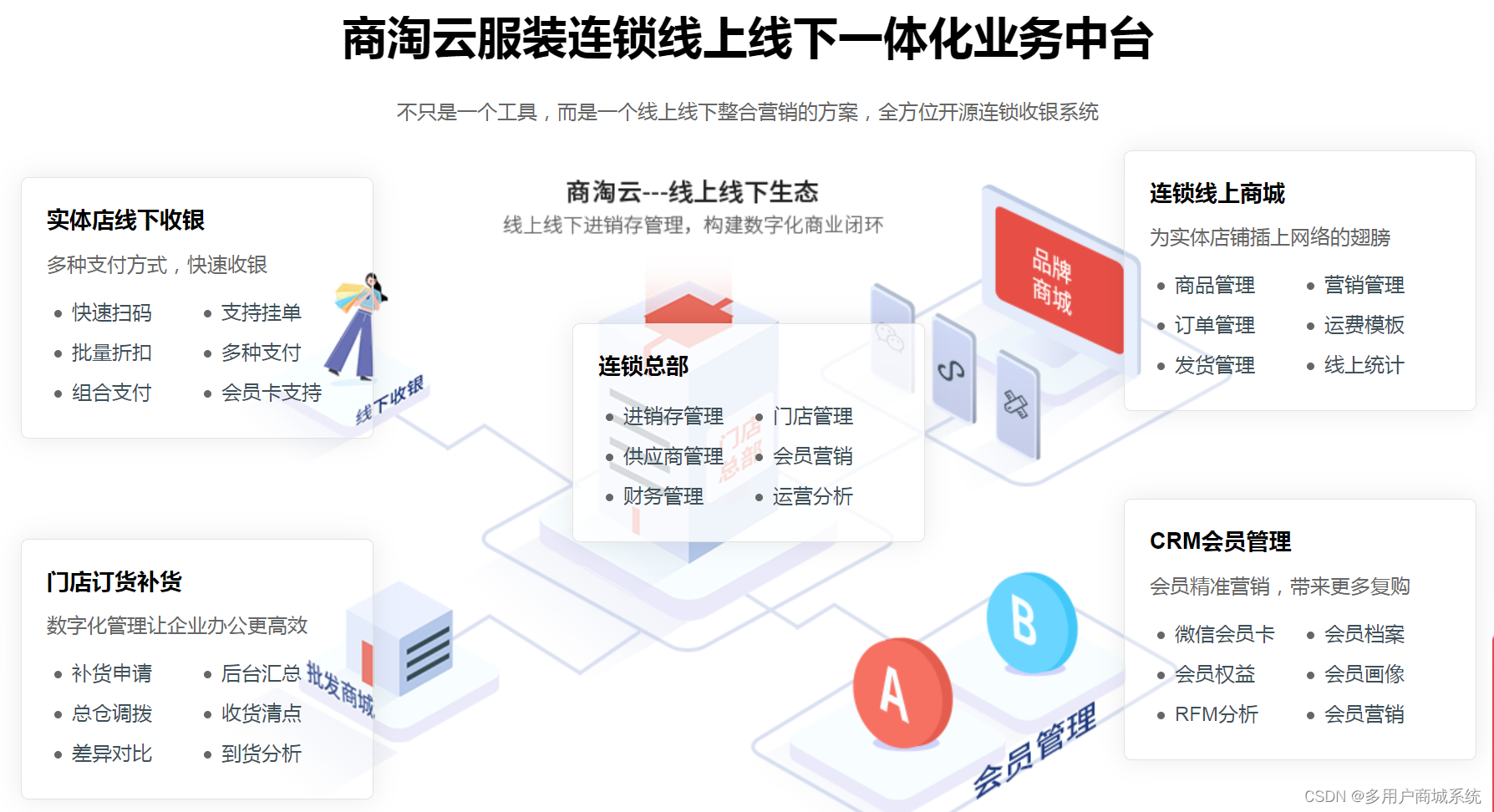
开源收银系统在服装连锁店中发挥的重要作用
在当今竞争激烈的零售市场中,服装连锁店面临着日益复杂的经营环境和多样化的消费需求。在这样的背景下,开源收银系统成为了服装连锁店管理的关键利器。该系统不仅提供了高效的收银功能,还涵盖了进销存管理、会员管理、门店补货等多方面功能&a…...

代码随想录三刷day51
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣200. 岛屿数量二、力扣695. 岛屿的最大面积三、力扣1020. 飞地的数量四、力扣130. 被围绕的区域 前言 依然是从地图周边出发,将周边空格相邻…...

基于python+Django的二维码生成算法设计与实现
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...
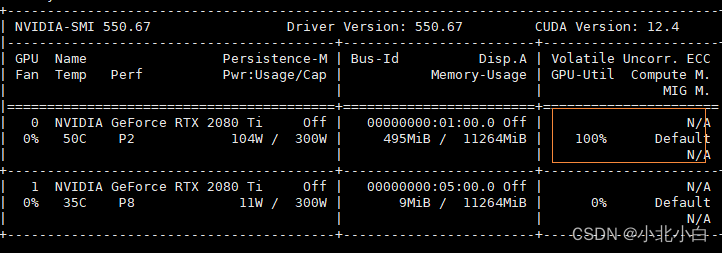
pytorch 2.0 多线程并行,导致GPU利用100%,卡住
背景: 程序中有pytorch模型两个,yolov5,crnn。 之前无论是pth格式,还是TRT格式,并行的都没有问题。 最近发现,多线程ThreadPoolExecutor(max_workers2)调用的时候,即单个进程内处理一张图像&a…...

后端开发面经系列 -- 阿里C++二面面经
阿里C二面面经 公众号:阿Q技术站 来源:https://www.nowcoder.com/feed/main/detail/fc4a48403b534aafa6a6bce14b542c4e?sourceSSRsearch 1、智能指针? std::shared_ptr: 原理:std::shared_ptr是基于引用计数的智能指…...
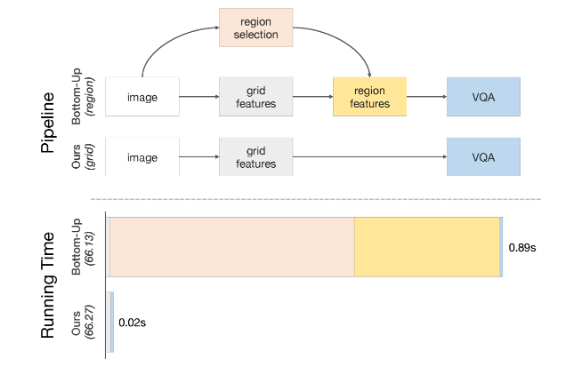
【Image captioning】In Defense of Grid Features for Visual Question Answering实现流程
In Defense of Grid Features for Visual Question Answering实现流程 网格特征预训练代码 这是该论文的特征预训练代码发布: @InProceedings{jiang2020defense,title={In Defense of Grid Features for Visual Question Answering},author={Jiang, Huaizu and Misra, Ishan…...
MySQL用SQL取三列中最大的数据值
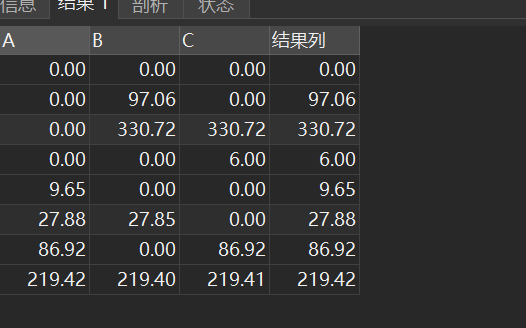
1、有如下数据: ABC000097.0600330.72330.720069.650027.8827.85086.92086.92219.42219.4219.41 需要展示为如下形式: ABC结果列0000097.06097.060330.72330.72330.7200669.65009.6527.8827.85027.8886.92086.9286.92219.42219.4219.41219.42 解决办…...

【Mac】如何解决打开PD虚拟机后Mac无法上网的问题?
问题描述 部分用户在运行Parallels Desktop并打开Windows 11后,发现Windows上网没有问题,但是Mac主机不能访问带域名的网站,而访问带IP的网站没问题,退出Parallels虚拟机以后,Mac网络又恢复正常。 解决办法 退出 Pa…...
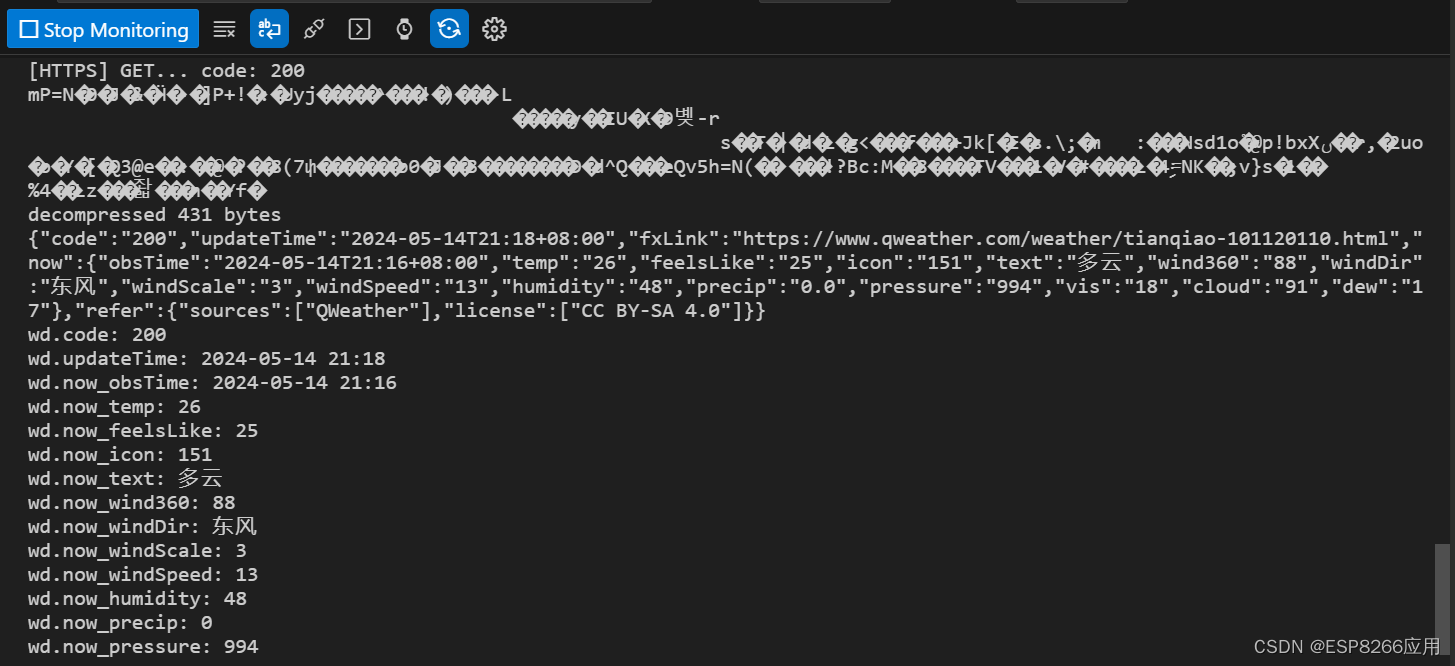
【NodeMCU实时天气时钟温湿度项目 7】和风天气API返回JSON数据信息的解压缩实现——ArduinoUZlib功能库
今天是第七专题,主要内容是:导入ArduinoUZlib功能库,借助该库把从【和风天气】官网返回的经过Gzip压缩的JSON数据,进行解压缩和t解析,在串口监视器上输出解析后的JSON信息。 如您需要了解其它专题的内容,请…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
