机器学习中常用的几种距离——欧式、余弦等
目录
- 一、欧式距离(L2距离)
- 二、曼哈顿距离(L1距离)
- 三、汉明距离
- 四、余弦相似度
一、欧式距离(L2距离)
(1)二维空间的距离公式(三维空间的在这个基础上类推):
A(x1,y1),B(x2,y2)两点之间的欧式距离为:
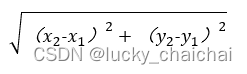
(2)n维空间的距离公式
A(x1,x2,…,xn)和B(x21,x22,…,x2n)两点之间的欧式距离为:
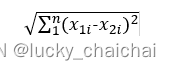
二、曼哈顿距离(L1距离)
就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投射的距离总和。
如下图中,红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的
曼哈顿距离。

(1)二维空间的曼哈顿距离公式:
- A(x1,y1),B(x2,y2)两点之间的曼哈顿距离为:
dAB = |x1 - x2| + |y1 - y2|
(2)n维空间的曼哈顿距离公式:
- A(x1,x2,…,xn)和B(x21,x22,…,x2n)两点之间的曼哈顿距离为:

三、汉明距离
编辑距离。两个等⻓字符串s1与s2的汉明距离为:将其中⼀个变为另外⼀个所需要作的最⼩字符替换次数。
【注意:】
编辑距离与汉明距离相比,编辑距离不要求两个字符串的长度等长,他追求的是如何以最少的编辑(替换,插入,删除,位置交换)次数让两个字符串相同。
四、余弦相似度
两个⼆维空间中向量A(x1,y1)与向量B(x2,y2)的夹⻆余弦公式:
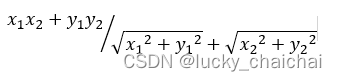
两个n维样本点A(x1,x12,…,x1n)和B(x21,x22,…,x2n)的夹⻆余弦为:
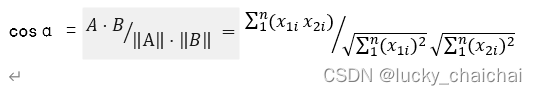
优缺点及其他距离待续。。。。。。
相关文章:
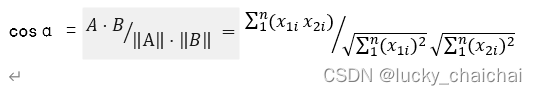
机器学习中常用的几种距离——欧式、余弦等
目录 一、欧式距离(L2距离)二、曼哈顿距离(L1距离)三、汉明距离四、余弦相似度 一、欧式距离(L2距离) (1)二维空间的距离公式(三维空间的在这个基础上类推)&…...

2024 Google I/O Android 相关内容汇总
2024 Google I/O Android 相关内容汇总 本次 Google I/O 的核心虽然是 AI ,但是 Android 也是作为主要议题出现, Android 部分可以简单分为产品和开发相关内容,接下来主要介绍这两部分的相关更新。 重点开始开发相关,内容不少 产…...
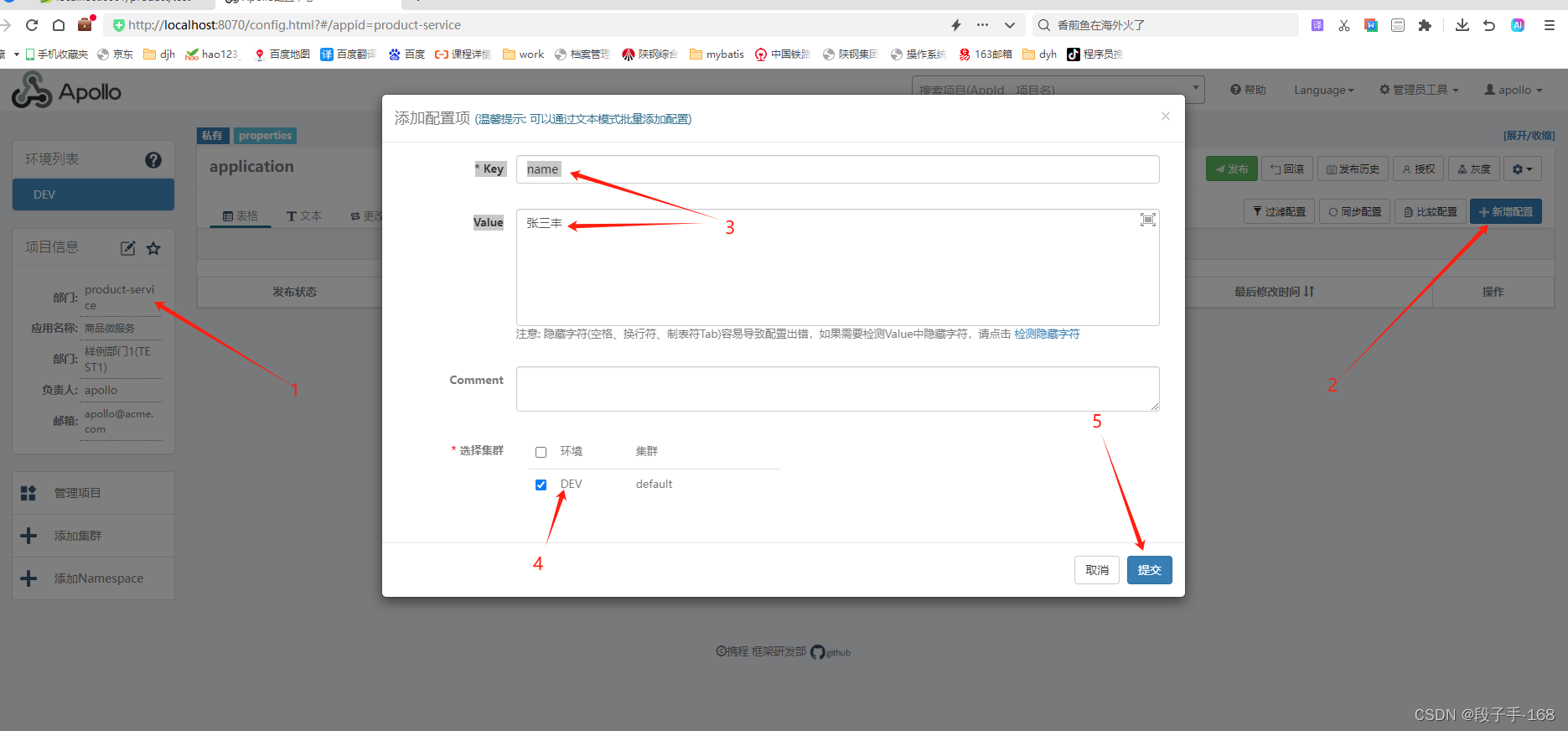
# 从浅入深 学习 SpringCloud 微服务架构(十八)
从浅入深 学习 SpringCloud 微服务架构(十八) 一、开源配置中心 Apollo:概述 1、开源配置中心 Apollo Apollo -A reliable configuration management system Apollo(阿波罗)是携程框架部门研发的分布式配置中心,能够集中化管理…...

在SQL Server中使用临时表与普通表的性能差异分析
在SQL Server中,临时表和普通表的性能确实存在差异,具体表现和影响因素如下: 临时表和普通表的区别 存储位置: 临时表:存储在tempdb数据库中,生命周期仅限于当前会话或批处理。当会话结束或批处理完成时&a…...
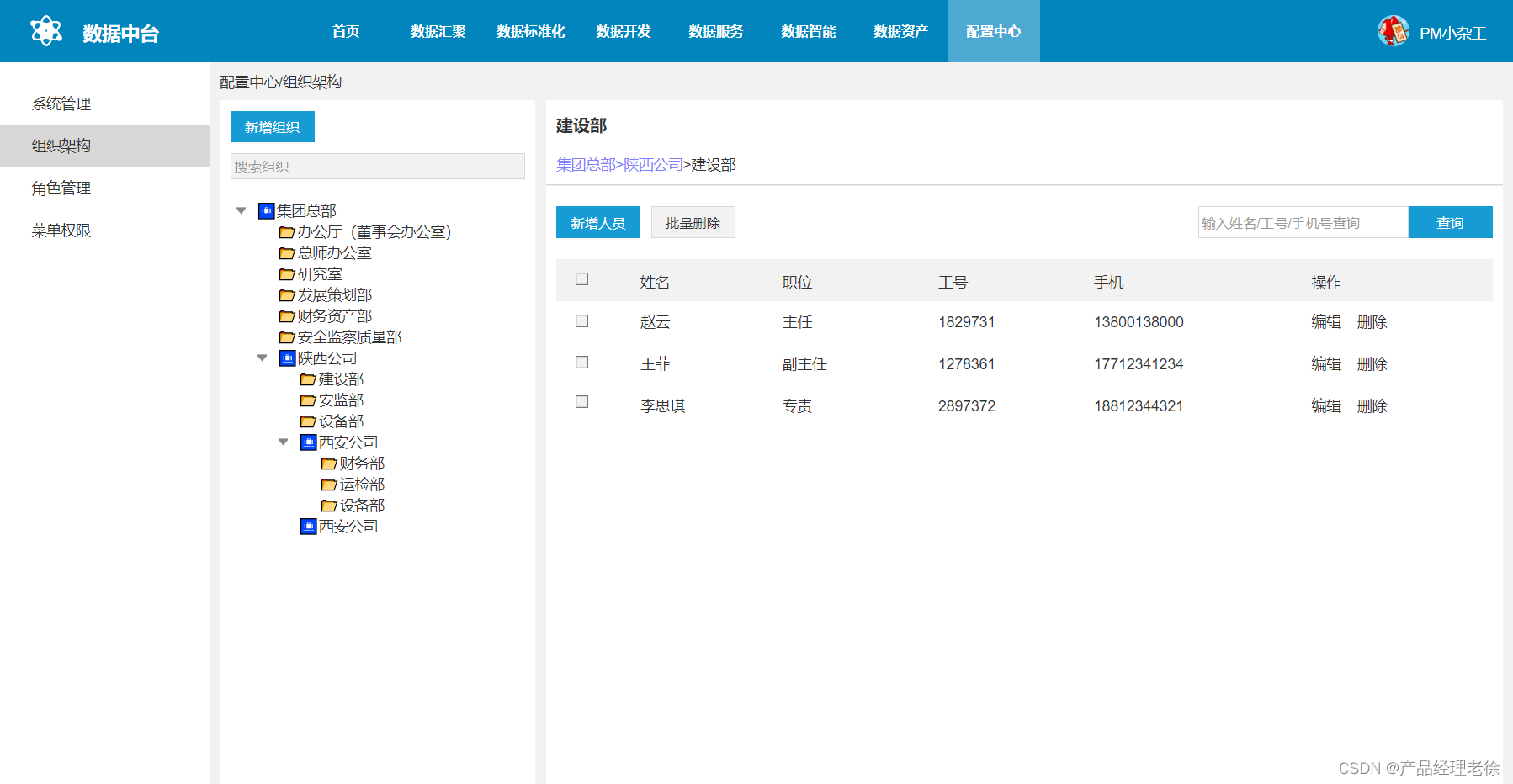
数据中台管理系统原型
数据中台是一个通用性的基础平台,适用于各类行业场景,数据中台包含多元数据汇聚、数据标准化、数据开发、数据共享、数据智能、数据资产管理等功能,助力企业数字化转型。 数据汇聚 数据汇聚是将不同系统、不同类型的多元源数据汇聚至目标数据…...

数据库练习
在数据库中创建一个表student,用于存储学生信息 CREATE TABLE student( id INT PRIMARY KEY, name VARCHAR(20) NOT NULL, grade FLOAT ); 1、向student表中添加一条新记录(记录中id字段的值为1,name字段的值为"monkey",…...
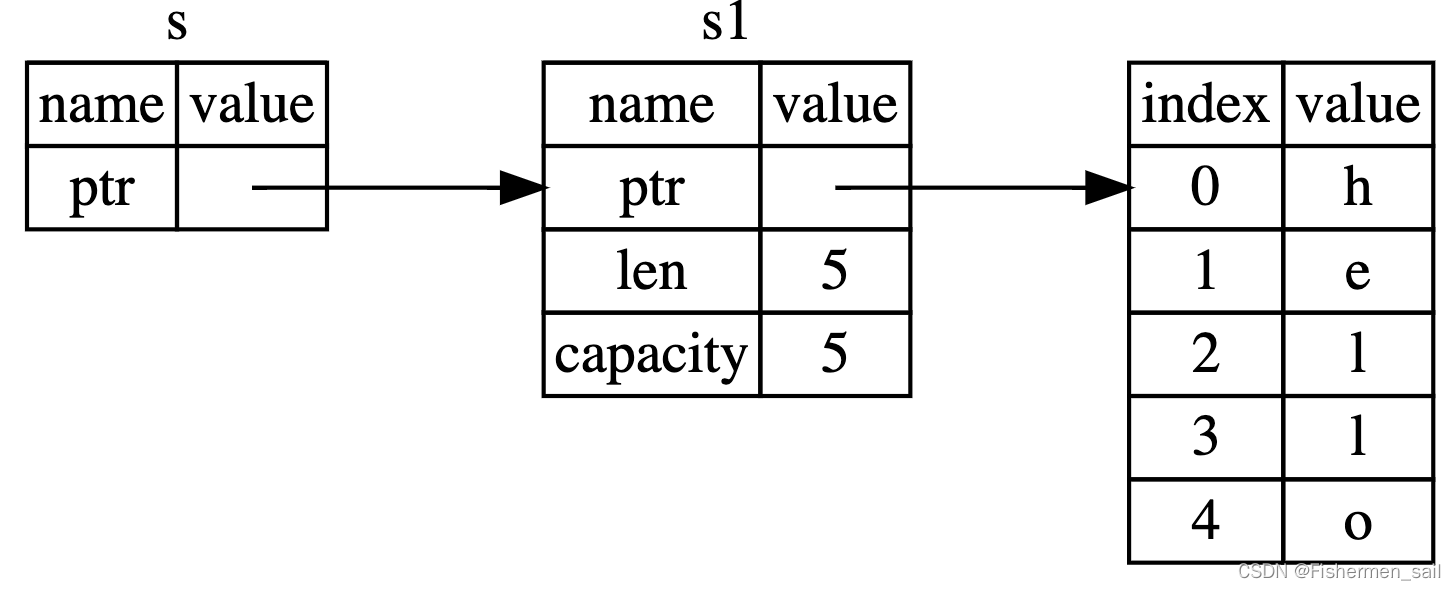
Rust学习笔记(上)
前言 笔记的内容主要参考与《Rust 程序设计语言》,一些也参考了《通过例子学 Rust》和《Rust语言圣经》。 Rust学习笔记分为上中下,其它两个地址在Rust学习笔记(中)和Rust学习笔记(下)。 编译与运行 Ru…...

【SRC实战】文件名回显导致反射型XSS,URL重定向
挖个洞先 https://mp.weixin.qq.com/s/hnrm-snkETuR-gqPOSnQXQ “ 以下漏洞均为实验靶场,如有雷同,纯属巧合 ” 01 — 漏洞证明 一、反射型XSS “ 文件名回显,能否触发XSS?” 1、灯塔扫到敏感文件,发现1.txt会在…...

mysql高版本导入低版本Unknown collation: utf8mb4_0900_ai_ci
MySQL数据库导入SQL报错 Unknown collation: ‘utf8mb4_0900_ai_ci‘ 错误原因:我本地的MySQL数据包版本为8.0的,而服务器上的MySQL版本为5.7,双方的版本不兼容,这样就导致我在本地写好的SQL无法在服务器上的MySQL上运行。 解决办…...

运筹说 第114期 | 其他排队模型简介
前面我们已经学习了一些排队模型,对排队系统有了基本认知,本期小编带大家继续来学习其他排队模型的内容。 一、有限源排队模型 顾客源为有限的这类排队问题的主要特征是顾客总数是有限的,如只有m个顾客。每个顾客来到系统中接受服务后仍回到…...

易基因: WGBS等揭示梨驯化和改良过程中DNA甲基化对果实成熟的作用机制 | 作物育种
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。 梨(Pyrus ssp.,蔷薇科杏仁核亚科)是世界上最重要的温带水果作物之一。与野生梨相比,栽培梨的果实在许多形态特征上表现出显著变化…...

数据分析(二)——导入外部数据,导入Excel数据,CSV文件,txt文件,HTML网页,数据抽取,DataFrame对象的loc属性与iloc属性
一.导入外部数据 1.导入.xIs或.xIsx文件 pd.read_ excel(io,sheet_ name,header) 1.1常用参数说明 ●io:表示.xIs或.xIsx文件路径或类文件对象 ●sheet name:表示工作表,取值如下表所示 ●header:默认值为0,取第一行的值为列名,数据为除列…...

如何让Linux系统崩溃?
如何使 Linux 系统崩溃 警告 下面的代码行是 Bash shell 的一个简短而甜蜜的 fork 炸弹。分叉炸弹之所以有效,是因为它能够产生无限数量的进程。最终,Linux无法处理所有这些,并且会崩溃。 fork 炸弹的一大优点是你不需要 root 权限即可执行它…...

C# 实现邮件推送功能
🏆作者:科技、互联网行业优质创作者 🏆专注领域:.Net技术、软件架构、人工智能、数字化转型、DeveloperSharp、微服务、工业互联网、智能制造 🏆欢迎关注我(Net数字智慧化基地),里面…...

企业微信私域营销:构建高效转化新引擎
在数字营销的大潮中,企业微信作为企业内部沟通协作的重要工具,也逐渐成为企业私域营销的重要战场。本文将带您深入了解企业微信私域营销的魅力,探讨如何构建高效转化的新引擎。 一、企业微信私域营销:为何重要? 企业微…...
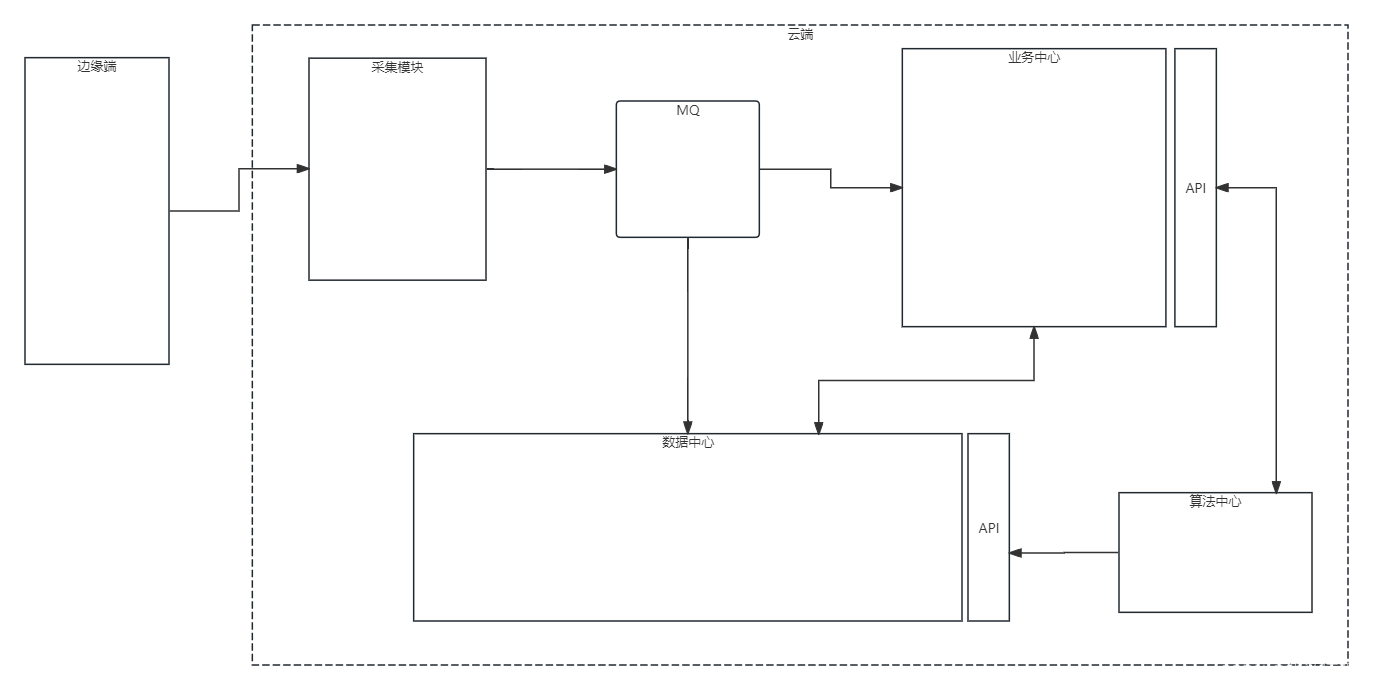
电力物联网-(2)系统设计
电力物联网系统设计 前言 在此之前写过《电力物联网系统设计》开篇文章,上一篇文章主要的概述性的内容,发表之后总觉得对电力物联网系统设计这一方面还只是开了一个头,没有把相关的内容讲解清楚,于是经过一段时间的构思终于产出了…...
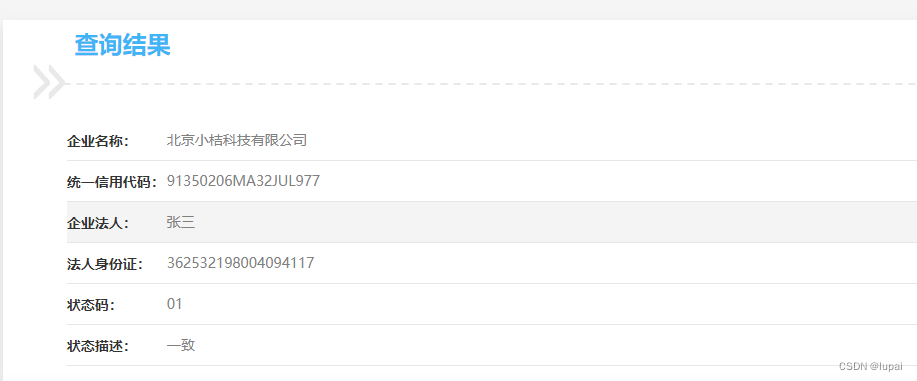
如何确保企业信息的真实性和可靠性,保障企业权益、降低合作风险
企业四要素核验:确保企业信息真实性的关键步骤 随着信息技术的飞速发展,企业信息的准确性和可靠性对于商业决策、合作伙伴选择以及风险管理等方面都显得尤为重要。为了确保企业信息的真实性和可靠性,企业四要素核验成为了一项关键步骤。本文…...

用python写一个自动生成android开机动画的工具
要创建一个自动生成Android开机动画的工具,你需要一些基本的知识,比如Python编程、图像处理和Android开机动画的格式。以下是一个简单的Python脚本示例,它可以生成一个基本的Android开机动画,具体效果可能需要更多的调整和优化。 …...

玩机进阶教程------MTK机型重置账号 去除FRP 去除开机密码 清除数据的几种方法步骤解析
目前的机型不管是高通芯片还是MTK芯片。都有账号类限制。包含云账号 frp账号和开机密码等等,他们在线刷包中对应的分区是不同的。例如针对开机图案密码这些,有些机型靠简单的恢复出厂是无效果的,其实对应的解决方法很简单。今天将针对MTK芯片机型的账号问题做个步骤解析。 …...
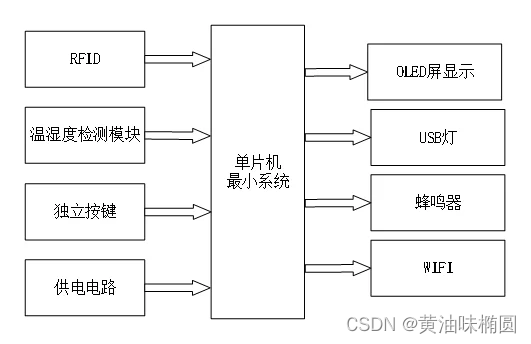
基于STM32单片机和RFID的智能仓库管理系统-设计说明书
设计摘要: 本设计是基于STM32单片机和RFID技术的智能仓库管理系统。系统主要具备以下功能:首先,将货物的名称和数量信息存储在RFID卡中,每个货物对应一个RFID卡,共有三个RFID卡。当需要进行出库或入库操作时ÿ…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
