动手学深度学习16 Pytorch神经网络基础
动手学深度学习16 Pytorch神经网络基础
- 1. 模型构造
- 2. 参数管理
- 1. state_dict()
- 2. normal_() zeros_()
- 3. xavier初始化
- 共享参数的好处
- 3. 自定义层
- 4. 读写文件
- net.eval() 评估模式
- QA
1. 模型构造
定义隐藏层–模型结构+定义前向函数–模型结构的调用
import torch
from torch import nn
from torch.nn import functional as F # functional定义了一些常用函数net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
X = torch.rand(2, 20)
print(net(X).shape)
print(net(X))
# torch.Size([2, 10])
# tensor([[-0.0363, -0.0911, 0.0992, 0.2046, 0.1297, -0.0435, 0.0289, -0.0135,
# 0.0162, -0.1780],
# [-0.0055, -0.1556, 0.2570, 0.1685, 0.2182, -0.0625, 0.1187, -0.2728,
# 0.0377, -0.0335]], grad_fn=<AddmmBackward0>)# 定义隐藏层 定义前向计算函数
class MLP(nn.Module):# 用模型参数声明层。这里,我们声明两个全连接的层def __init__(self):# 调用MLP的父类Module的构造函数来执行必要的初始化。# 这样,在类实例化时也可以指定其他函数参数,例如模型参数params(稍后将介绍)super().__init__()self.hidden = nn.Linear(20, 256) # 隐藏层self.out = nn.Linear(256, 10) # 输出层# 定义模型的前向传播,即如何根据输入X返回所需的模型输出def forward(self, X):# 注意,这里我们使用ReLU的函数版本,其在nn.functional模块中定义。# 定义网络的具体使用return self.out(F.relu(self.hidden(X)))
net = MLP()
print(net(X).shape)
print(net(X))
# torch.Size([2, 10])
# tensor([[-0.1424, -0.2162, 0.0554, -0.1324, 0.0053, -0.2589, 0.1554, 0.0185,
# -0.0261, -0.0273],
# [-0.1666, -0.2078, 0.1894, -0.0820, -0.0194, -0.3017, 0.1006, 0.0531,
# 0.0831, 0.0400]], grad_fn=<AddmmBackward0>)# Sequential的实现方法
class MySequential(nn.Module):def __init__(self, *args):super().__init__()for idx, module in enumerate(args):# 这里,module是Module子类的一个实例。我们把它保存在'Module'类的成员# 变量_modules中。_module的类型是OrderedDict# 把定义的网络结构传进来self._modules[str(idx)] = module # _models pytorch 特殊的容器def forward(self, X):# OrderedDict保证了按照成员添加的顺序遍历它们for block in self._modules.values():# block 遍历得到的传进来的每一个网络层X = block(X)return X
net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
print(net(X).shape)
print(net(X))
# torch.Size([2, 10])
# tensor([[ 0.0108, -0.2344, -0.1777, -0.2290, 0.0705, 0.3400, -0.1919, 0.1660,
# 0.2318, -0.1056],
# [ 0.0595, -0.2881, -0.2255, -0.2076, 0.1802, 0.3965, -0.1355, 0.1964,
# 0.2925, -0.0213]], grad_fn=<AddmmBackward0>)# 当Sequential不能满足需求,可以自定义需求,灵活定义参数和前向计算【反向计算就是自动求导】
class FixedHiddenMLP(nn.Module):def __init__(self):super().__init__()# 不计算梯度的随机权重参数。因此其在训练期间保持不变self.rand_weight = torch.rand((20, 20), requires_grad=False)self.linear = nn.Linear(20, 20)def forward(self, X):X = self.linear(X)# 使用创建的常量参数以及relu和mm函数X = F.relu(torch.mm(X, self.rand_weight)+ 1)print(X.shape) # torch.Size([2, 20])# 复用全连接层。这相当于两个全连接层共享参数X = self.linear(X)print(X.shape) # torch.Size([2, 20])# 控制流 一个while循环 控制数值的大小while X.abs().sum() > 1:X /= 2return X.sum()
net = FixedHiddenMLP()
print(net(X).shape)
print(net(X))
# torch.Size([])
# tensor(0.0029, grad_fn=<SumBackward0>)# 嵌套使用 套娃
class NestMLP(nn.Module):def __init__(self):super().__init__()self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),nn.Linear(64, 32), nn.ReLU())self.linear = nn.Linear(32, 16)def forward(self, X):return self.linear(self.net(X))chimera = nn.Sequential(NestMLP(), nn.Linear(16, 20), FixedHiddenMLP())
print(chimera(X).shape)
print(chimera(X))
# torch.Size([])
# tensor(-0.1322, grad_fn=<SumBackward0>)
torch.Size([2, 10])
tensor([[-0.1086, 0.0407, -0.0890, -0.1080, -0.1151, -0.0182, 0.0289, -0.0965,0.0719, 0.0070],[-0.1091, 0.1145, 0.0367, -0.1198, -0.1689, -0.0805, 0.0793, -0.1029,0.2269, 0.0136]], grad_fn=<AddmmBackward0>)
torch.Size([2, 10])
tensor([[-0.0402, -0.1168, 0.0247, -0.3162, 0.2468, -0.1404, -0.1788, 0.0155,-0.1886, 0.0299],[ 0.0485, 0.0026, 0.0997, -0.1873, 0.1532, -0.1166, -0.0506, -0.0015,-0.2233, -0.0393]], grad_fn=<AddmmBackward0>)
torch.Size([2, 10])
tensor([[-0.1543, 0.1518, 0.1331, 0.0212, 0.0276, -0.0971, -0.1083, 0.1020,0.0707, 0.1184],[-0.1344, 0.1214, 0.0972, -0.0816, -0.0061, -0.0984, 0.0359, 0.0151,0.0715, 0.1701]], grad_fn=<AddmmBackward0>)
torch.Size([2, 20])
torch.Size([2, 20])
torch.Size([])
torch.Size([2, 20])
torch.Size([2, 20])
tensor(0.2815, grad_fn=<SumBackward0>)
torch.Size([2, 20])
torch.Size([2, 20])
torch.Size([])
torch.Size([2, 20])
torch.Size([2, 20])
tensor(0.2898, grad_fn=<SumBackward0>)
2. 参数管理
课件:https://zh-v2.d2l.ai/chapter_deep-learning-computation/parameters.html

import torch
from torch import nnnet = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8,1))
X = torch.rand(size=(2, 4))
print(net(X).shape)
print(net(X))# torch.Size([2, 1])
# tensor([[-0.1604],
# [-0.2131]], grad_fn=<AddmmBackward0>)# 已经定义好类 参数怎么访问
# 5.2.1 参数访问
print(net)
# 权重可以被改变--认为是状态
print(net[2].state_dict()) # 根据索引访问网络结构的每一层 索引从0开始 nn.Linear(8,1) state_dict拿出每一层的参数
# Sequential(
# (0): Linear(in_features=4, out_features=8, bias=True)
# (1): ReLU()
# (2): Linear(in_features=8, out_features=1, bias=True)
# )
# OrderedDict([('weight', tensor([[-0.0700, 0.1160, -0.1421, -0.1165, -0.2099, -0.2973, -0.2147, 0.1907]])), ('bias', tensor([-0.0925]))])# 5.2.1.1 目标参数
# .符号访问类的属性和方法
print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data) # 访问值 .data 访问梯度 .grad
# <class 'torch.nn.parameter.Parameter'> # Parameter定义可以优化的参数
# Parameter containing:
# tensor([-0.1783], requires_grad=True)
# tensor([-0.1783])
print(net[2].weight.grad == None) # True 上面还没有做梯度 所有梯度是None# 5.2.1.2. 一次性访问所有参数
print(*[(name, param.shape) for name, param in net[0].named_parameters()])
print(*[(name, param.shape) for name, param in net.named_parameters()])
# 'weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
# relu层没有参数 所有下面是没有1 层的 因为没有参数所以拿不到
# ('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))
# 另一种访问网络参数的方式
print(net.state_dict()['2.bias'].data) # tensor([-0.0584])# 5.2.1.3. 从嵌套块收集参数
def block1():return nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 4), nn.ReLU())def block2():net = nn.Sequential()for i in range(4):# 在这里嵌套 调用4次block函数net.add_module(f'block{i}', block1())return netrgnet = nn.Sequential(block2(), nn.Linear(4, 1))
print(rgnet(X).shape)
print(rgnet(X))
# torch.Size([2, 1])
# tensor([[0.1651],
# [0.1651]], grad_fn=<AddmmBackward0>)
print(rgnet) # 分层嵌套 可以像通过嵌套列表索引一样访问它们 了解网络是什么样子
# Sequential(
# (0): Sequential(
# (block0): Sequential(
# (0): Linear(in_features=4, out_features=8, bias=True)
# (1): ReLU()
# (2): Linear(in_features=8, out_features=4, bias=True)
# (3): ReLU()
# )
# (block1): Sequential(
# (0): Linear(in_features=4, out_features=8, bias=True)
# (1): ReLU()
# (2): Linear(in_features=8, out_features=4, bias=True)
# (3): ReLU()
# )
# (block2): Sequential(
# (0): Linear(in_features=4, out_features=8, bias=True)
# (1): ReLU()
# (2): Linear(in_features=8, out_features=4, bias=True)
# (3): ReLU()
# )
# (block3): Sequential(
# (0): Linear(in_features=4, out_features=8, bias=True)
# (1): ReLU()
# (2): Linear(in_features=8, out_features=4, bias=True)
# (3): ReLU()
# )
# )
# (1): Linear(in_features=4, out_features=1, bias=True)
# )
# 分层嵌套 可以像通过嵌套列表索引一样访问它们 访问第一个主要的块中、第二个子块的第一层的偏置项
# 模型结构嵌套组成--字典数据格式, 每层模型及数据的访问都可以通过字典嵌套调用。
print(rgnet[0][1][0].bias.data)
# tensor([-0.2360, 0.1476, -0.2232, 0.3928, 0.1546, -0.3637, 0.0373, 0.1421])
# 复杂网络模块化 这样打印或者访问会方便很多。# 5.2.2. 参数初始化
# 5.2.2.1. 内置初始化
# 调用内置的初始化器 m 一个module
def init_normal(m):if type(m) == nn.Linear:# 带有下划线 替换函数 直接原地操作更改值# nn.init 有很多初始化的函数nn.init.normal_(m.weight, mean=0, std=0.01)nn.init.zeros_(m.bias)
# 对net的所有layer遍历,并调用init_normal
net.apply(init_normal)
print(net[0].weight.data[0], net[0].bias.data[0])
# tensor([ 0.0085, -0.0095, -0.0011, 0.0080]) tensor(0.)
# 可以初始化任意的值
def init_constant(m):if type(m) == nn.Linear:nn.init.constant_(m.weight, 1)nn.init.zeros_(m.bias)
net.apply(init_constant)
print(net[0].weight.data[0], net[0].bias.data[0])
# tensor([1., 1., 1., 1.]) tensor(0.)
# 为什么不能把参数全部初始化为常数?# Xavier初始化方法始化第一个神经网络层 可以对某些块应用不同的初始化方法
def init_xavier(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)def init_42(m):if type(m) == nn.Linear:nn.init.constant_(m.weight, 42) # 42 宇宙的答案?
# apply是module自己定义的函数,可以对不同的层apply不同的函数
net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)
# tensor([ 0.0490, 0.1516, -0.5191, -0.5409])
# tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])# 5.2.2.2. 自定义初始化
def my_init(m):if type(m) == nn.Linear:print("Init", *[(name, param.shape)for name, param in m.named_parameters()][0])nn.init.uniform_(m.weight, -10, 10)m.weight.data *= m.weight.data.abs() >= 5
net.apply(my_init)
print(net[0].weight[:2])# 直接对参数做替换
net[0].weight.data[:] += 1
net[0].weight.data[0,0] = 42
print(net[0].weight.data[0]) # 42# 5.2.3. 参数绑定 再不同网络层间共享权重
# 我们需要给共享层一个名称,以便可以引用它的参数
# 因为两个share是同一个内存,数据都是一样的
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),shared, nn.ReLU(), shared, nn.ReLU(), nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
# tensor([True, True, True, True, True, True, True, True])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象,而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])
# tensor([True, True, True, True, True, True, True, True])
"""
这个例子表明第三个和第五个神经网络层的参数是绑定的。
它们不仅值相等,而且由相同的张量表示。
因此,如果我们改变其中一个参数,另一个参数也会改变。
这里有一个问题:当参数绑定时,梯度会发生什么情况?
答案是由于模型参数包含梯度,因此在反向传播期间第二个隐藏层 (即第三个神经网络层)和第三个隐藏层(即第五个神经网络层)的梯度会加在一起。
"""
torch.Size([2, 1])
tensor([[0.1068],[0.0465]], grad_fn=<AddmmBackward0>)
Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=1, bias=True)
)
OrderedDict([('weight', tensor([[ 0.1080, -0.1647, 0.2971, 0.1225, -0.3232, 0.0757, 0.2715, -0.0025]])), ('bias', tensor([-0.2136]))])
<class 'torch.nn.parameter.Parameter'>
Parameter containing:
tensor([-0.2136], requires_grad=True)
tensor([-0.2136])
True
('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))
tensor([-0.2136])
torch.Size([2, 1])
tensor([[0.5388],[0.5388]], grad_fn=<AddmmBackward0>)
Sequential((0): Sequential((block0): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block1): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block2): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block3): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU()))(1): Linear(in_features=4, out_features=1, bias=True)
)
tensor([-0.1184, -0.4867, 0.1143, 0.0433, -0.0099, 0.3492, 0.0243, 0.4199])
tensor([-0.0013, 0.0126, -0.0083, -0.0063]) tensor(0.)
tensor([1., 1., 1., 1.]) tensor(0.)
tensor([ 0.1240, 0.0555, -0.1999, -0.0746])
tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])
Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])
tensor([[-0.0000, 5.5928, -0.0000, -0.0000],[-0.0000, 0.0000, -6.6817, -0.0000]], grad_fn=<SliceBackward0>)
tensor([True, True, True, True, True, True, True, True])
tensor([True, True, True, True, True, True, True, True])
这个例子表明第三个和第五个神经网络层的参数是绑定的。 它们不仅值相等,而且由相同的张量表示。 因此,如果我们改变其中一个参数,另一个参数也会改变。 这里有一个问题:当参数绑定时,梯度会发生什么情况? 答案是由于模型参数包含梯度,因此在反向传播期间第二个隐藏层 (即第三个神经网络层)和第三个隐藏层(即第五个神经网络层)的梯度会加在一起。
1. state_dict()
state_dict() 是PyTorch中用于获取模型的状态字典(state dictionary)的方法。在PyTorch中,模型的状态字典是一个Python字典对象,其中包含了模型的所有可学习参数和缓冲区(如卷积层的权重和偏置、BatchNorm层的均值和方差等)。具体来说,state_dict() 方法返回一个字典,字典的键是参数的名称,值是对应参数的张量(Tensor)。
对于神经网络模型 net,通过调用 net.state_dict() 可以获取模型的状态字典。这个状态字典通常用于保存和加载模型的参数,以及在训练过程中进行模型状态的保存和恢复。
例如,可以使用 torch.save(net.state_dict(), 'model.pth') 将模型的状态字典保存到文件中,然后使用 net.load_state_dict(torch.load('model.pth')) 加载保存的模型参数。这样可以方便地保存和加载模型的参数,而无需保存整个模型。
2. normal_() zeros_()
nn.init.normal_() 和 nn.init.zeros_() 是PyTorch中用于初始化模型参数的函数。
-
nn.init.normal_(tensor, mean=0, std=0.01):- 这个函数用于对输入的张量
tensor进行正态分布初始化。其中,mean参数表示正态分布的均值,默认值为0;std参数表示正态分布的标准差,默认值为0.01。调用这个函数会将tensor中的值按照指定的正态分布进行初始化。
- 这个函数用于对输入的张量
-
nn.init.zeros_(tensor):- 这个函数用于将输入的张量
tensor中的值全部初始化为0。调用这个函数会将tensor中的所有元素都设置为0。
- 这个函数用于将输入的张量
这些初始化函数通常在定义模型的时候用来初始化模型的权重和偏置等参数。例如,在定义一个全连接层时,可以使用 nn.init.normal_(m.weight, mean=0, std=0.01) 来初始化权重为正态分布,使用 nn.init.zeros_(m.bias) 来初始化偏置为0。这有助于在模型训练时使得参数的初始值处于合适的范围,有助于模型的训练和收敛。
在PyTorch中,函数名带有下划线(例如nn.init.normal_()和nn.init.zeros_())的函数通常是就地(in-place)操作,而不带下划线的函数则是返回新的张量或对象。
具体来说,带下划线的函数会直接修改传入的张量或对象,并在原地进行操作,而不带下划线的函数则会返回一个新的张量或对象,而不会修改原始的输入。这种设计可以有效地节省内存,特别是当处理大规模数据时。
举个例子,nn.init.normal_(tensor, mean=0, std=0.01)会就地地将张量tensor按照正态分布进行初始化,并且不返回任何值,而nn.init.normal(tensor, mean=0, std=0.01)则会返回一个新的张量,而不会修改原始的tensor。
因此,如果需要在原地进行操作而不创建新的对象,可以使用带下划线的函数;如果需要保留原始对象并返回新的对象,则可以使用不带下划线的函数。
3. xavier初始化
nn.init.xavier_uniform_() 是PyTorch中用于对权重进行 Xavier 初始化的函数之一。
Xavier 初始化是一种常用的权重初始化方法,旨在帮助提高神经网络的训练速度和稳定性。它根据输入和输出的维度自动确定权重的初始化范围,以便在前向传播和反向传播过程中避免梯度消失或梯度爆炸等问题。
具体来说,nn.init.xavier_uniform_(m.weight) 的作用是对输入的权重张量 m.weight 进行 Xavier 初始化。这个函数会按照 Xavier 初始化的规则来初始化权重张量的值,而不返回任何值。使用这种初始化方法可以有助于提高神经网络模型的训练效果和收敛速度。
Xavier初始化是一种常用的权重初始化方法,旨在解决神经网络训练过程中的梯度消失和梯度爆炸问题,有助于提高训练速度和收敛性。
Xavier初始化的原理是根据输入和输出的维度自适应地初始化权重参数,使得输入和输出的方差保持一致。具体来说,Xavier初始化的公式如下:
Xavier初始化 = 随机初始化的权重 输入层维度 \text{Xavier初始化} = \frac{\text{随机初始化的权重}}{\sqrt{\text{输入层维度}}} Xavier初始化=输入层维度随机初始化的权重
或者可以根据激活函数的特性进行调整,如使用sigmoid函数时的Xavier初始化为:
Xavier初始化 = 随机初始化的权重 输入层维度 + 输出层维度 2 \text{Xavier初始化} = \frac{\text{随机初始化的权重}}{\sqrt{\frac{\text{输入层维度} + \text{输出层维度}}{2}}} Xavier初始化=2输入层维度+输出层维度随机初始化的权重
Xavier初始化的目的是使得每一层的输入和输出的方差尽可能相等,这样可以避免在深度神经网络中,梯度在传播过程中逐渐变小或变大,导致梯度消失或梯度爆炸的问题。这种初始化方法在一定程度上有助于加速模型的收敛和提高模型的训练效果。
PyTorch中的nn.init.xavier_uniform_()函数就是基于Xavier初始化原理设计的,用于对权重进行Xavier初始化。
共享参数的好处
共享参数通常可以节省内存,并在以下方面具有特定的好处:
对于图像识别中的CNN,共享参数使网络能够在图像中的任何地方而不是仅在某个区域中查找给定的功能。
对于RNN,它在序列的各个时间步之间共享参数,因此可以很好地推广到不同序列长度的示例。
对于自动编码器,编码器和解码器共享参数。 在具有线性激活的单层自动编码器中,共享权重会在权重矩阵的不同隐藏层之间强制正交。
3. 自定义层
# 5.4. 自定义层
# 5.4.1. 不带参数的层
# 构造一个没有任何参数的自定义层。CenteredLayer类要从其输入中减去均值。
import torch
import torch.nn.functional as F
from torch import nnclass CenteredLayer(nn.Module):def __init__(self):super().__init__()def forward(self, X):return X - X.mean()
layer = CenteredLayer()
layer(torch.FloatTensor([1,2,3,4,5]))
# tensor([-2., -1., 0., 1., 2.])# 将层作为组件合并到更复杂的模型中
net = nn.Sequential(nn.Linear(8, 128), nn.Linear(128, 8), CenteredLayer())
Y = net(torch.rand(4, 8))
print(Y)
print(Y.mean())
# tensor([[ 0.0464, -0.1820, -0.1769, -0.3194, 0.2035, -0.1366, 0.1352, -0.0289],
# [ 0.0922, -0.1399, -0.2116, -0.1318, 0.3869, -0.1489, 0.1342, -0.1571],
# [ 0.1539, 0.0276, -0.0175, -0.1465, 0.4049, -0.1203, 0.0870, -0.0523],
# [ 0.1634, -0.1678, -0.1643, -0.0143, 0.4284, -0.0157, 0.1687, -0.1003]],
# grad_fn=<SubBackward0>)
# tensor(-3.7253e-09, grad_fn=<MeanBackward0>)# 5.4.2. 带参数的层
# 这些参数可以通过训练进行调整。
# 可以使用内置函数来创建参数,这些函数提供一些基本的管理功能。 比如管理访问、初始化、共享、保存和加载模型参数。
# 这样做的好处之一是:我们不需要为每个自定义层编写自定义的序列化程序。
# 定义带参数的层 需要通过nn.parameter把参数包起来
class MyLinear(nn.Module):def __init__(self, in_units, units):super().__init__()self.weight = nn.Parameter(torch.randn(in_units, units))self.bias = nn.Parameter(torch.randn(units, ))def forward(self, X):linear = torch.matmul(X, self.weight.data) + self.bias.datareturn F.relu(linear)
linear = MyLinear(5, 3)
print(linear.weight)
# Parameter containing:
# tensor([[-1.8785, 0.3790, -0.4595],
# [-1.4118, -1.2047, 1.0940],
# [ 0.9223, 0.2497, 0.8488],
# [ 1.5715, -0.0039, -0.7107],
# [ 0.4815, -0.6535, -1.0387]], requires_grad=True)
print(linear(torch.rand(2, 5)))
# tensor([[0., 0., 0.],
# [0., 0., 0.]])
# 把自己构建的网络实例放到sequential里面调用
net = nn.Sequential(MyLinear(64, 8), MyLinear(8, 1))
print(net(torch.rand(2, 64)))
# tensor([[0.6376],
# [2.8535]])
tensor([[ 0.0782, -0.5266, 0.1779, 0.4015, 0.3536, -0.0918, 0.0110, -0.3319],[ 0.1765, -0.2833, 0.0191, 0.4218, 0.1403, -0.1637, 0.2045, -0.4312],[ 0.0750, -0.4275, 0.1780, 0.4071, 0.2387, -0.1722, 0.0852, -0.2727],[ 0.1671, -0.3559, 0.1018, 0.3969, 0.1400, -0.4335, 0.0391, -0.3228]],grad_fn=<SubBackward0>)
tensor(3.7253e-09, grad_fn=<MeanBackward0>)
Parameter containing:
tensor([[-0.4975, -0.0235, 0.4451],[ 0.0074, -0.3254, 0.4707],[ 0.9050, -0.7195, 1.9416],[ 1.3018, 1.3912, -0.5356],[-1.2469, 0.2616, -0.2979]], requires_grad=True)
tensor([[0.3865, 0.0000, 1.7432],[0.0000, 0.0000, 2.2532]])
tensor([[0.6376],[2.8535]])
4. 读写文件
保存加载模型参数:训练完的参数怎么保存下来。
# 5.5. 读写文件
# 5.5.1. 加载和保存张量
import torch
from torch import nn
from torch.nn import functional as f# 存储单个张量
x = torch.arange(4)
torch.save(x, 'x-file') # 保存到当前目录 x-file文件中x2 = torch.load('x-file') # 加载文件 读取文件的数据到内存
print(x2)# 存储张量列表
y = torch.zeros(4)
torch.save([x, y], 'x-files')
x2, y2 = torch.load('x-files')
print((x2, y2))
# (tensor([0, 1, 2, 3]), tensor([0., 0., 0., 0.]))# 存储张量字典
mydict = {'x':x, 'y':y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')
print(mydict2)
# {'x': tensor([0, 1, 2, 3]), 'y': tensor([0., 0., 0., 0.])}# 5.5.2. 加载和保存模型参数
# 保存整个模型,并在以后加载它们 将保存模型的参数而不是保存整个模型
class MLP(nn.Module):def __init__(self):super().__init__()self.hidden = nn.Linear(20, 256)self.output = nn.Linear(256, 10)def forward(self, x):return self.output(F.relu(self.hidden(x)))
net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)# net.state_dict() 只保存模型参数 不保存模型结构
# 所有参数存成一个字典。
torch.save(net.state_dict(), 'mlp.params')
clone = MLP()
# 要先定义--声明好模型结构【模型会随机初始化】,才能把模型参数填充到模型结构里面去,覆盖掉初始化的参数。
clone.load_state_dict(torch.load('mlp.params'))
clone.eval() # 测试不更新梯度
# MLP(
# (hidden): Linear(in_features=20, out_features=256, bias=True)
# (output): Linear(in_features=256, out_features=10, bias=True)
# )
Y_clone = clone(X)
print(Y_clone == Y)
# tensor([[True, True, True, True, True, True, True, True, True, True],
# [True, True, True, True, True, True, True, True, True, True]])
tensor([0, 1, 2, 3])
(tensor([0, 1, 2, 3]), tensor([0., 0., 0., 0.]))
{'x': tensor([0, 1, 2, 3]), 'y': tensor([0., 0., 0., 0.])}
MLP((hidden): Linear(in_features=20, out_features=256, bias=True)(output): Linear(in_features=256, out_features=10, bias=True)
)
tensor([[True, True, True, True, True, True, True, True, True, True],[True, True, True, True, True, True, True, True, True, True]])
模型参数保存与加载 https://blog.csdn.net/weixin_42831564/article/details/134789998
net.eval() 评估模式
在神经网络中,clone.eval()通常是指调用clone对象的eval()方法。这个方法通常用于将神经网络模型切换到评估模式。在评估模式下,模型的行为可能会有所不同,例如在训练时会关闭一些特定的训练相关操作,以便在测试或推断阶段得到更准确的结果。这种模式切换通常用于确保模型在不同阶段的运行行为是一致且正确的。
QA


1: 存成稀疏矩阵;不应该用ono-hot encoding,自然语言处理。
2:不知道怎么处理就直接先丢掉
3:MLP的QA有讲过,没有很好的办法。
4:实现的是两个函数,net(x) 是调用的net.__ call__()函数,也可以用net.foward()调用,但是nn里面已经做了映射
5:forward()函数是神经网络定义,对着论文公式敲出来的。
6:何凯明初始化,根据输入输出做一些初始化。初始化的主要目标是为了在模型一开始的时候在一个尺度上,不要到训练后期炸掉或者消失。
7:创建网络后,torch是按照什么规则给参数初始化的。
mxnet在-0.07,0.07之间均匀做初始化。
8:几乎没有不可导的函数,只是不会是处处可导。实际数值运算很少遇见。SVG可能求起来比较麻烦,但仍是可导的。
9:每一层是怎么定义的?后续会讲.
相关文章:

动手学深度学习16 Pytorch神经网络基础
动手学深度学习16 Pytorch神经网络基础 1. 模型构造2. 参数管理1. state_dict()2. normal_() zeros_()3. xavier初始化共享参数的好处 3. 自定义层4. 读写文件net.eval() 评估模式 QA 1. 模型构造 定义隐藏层–模型结构定义前向函数–模型结构的调用 import torch from torch…...
前端无样式id或者class等来定位标签
目录: 1、使用背景2、代码处理 1、使用背景 客户使用我们产品组件,发现替换文件,每次替换都会新增如下的样式,造就样式错乱,是组件的文件,目前临时处理的话就是替换文件时删除新增的样式,但是发…...

机器人工具箱学习(三)
一、动力学方程 机器人的动力学公式描述如下: 式中, τ \boldsymbol{\tau} τ表示关节驱动力矩矢量; q , q ˙ , q \boldsymbol{q} ,\; \dot{\boldsymbol { q }} ,\; \ddot{\boldsymbol { q }} q,q˙,q分别为广义的关节位置、速度和加速…...

华为OD机试 - CPU算力分配(Java 2024 C卷 100分)
华为OD机试 2024C卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷C卷)》。 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测试…...
web前端框架设计第八课-表单控件绑定
web前端框架设计第八课-表单控件绑定 一.预习笔记 1.v-model实现表单数据双向绑定 2.搜索数据的实现 3.全选案例实现1—JQ方法 4.单选案例实现 5.数据级联(二级级联) 6.v-model中的修饰符 二.课堂笔记 三.课后回顾 –行动是治愈恐惧的良药,…...
这三个网站我愿称之为制作答辩PPT的神
很多快要毕业的同学在做答辩PPT的时候总是感觉毫无思路,一窍不通。但这并不是你们的错,对于平时没接触过相关方面,第一次搞答辩PPT的人来说,这是很正常的一件事。一个好的答辩PPT可以根据以下分为以下几部分来写。 1.研究的背景和…...

flutter开发实战-实现多渠道打包及友盟统计(亲测有效)
flutter开发实战-实现多渠道打包及友盟统计(亲测有效) 最近开发过程中,需要引入友盟进行统计服务。友盟统计还需要区分不同渠道的打开应用的情况,所以需要处理多渠道打包的问题。 一、引入友盟统计 在工程的pubspec.yaml中引入…...
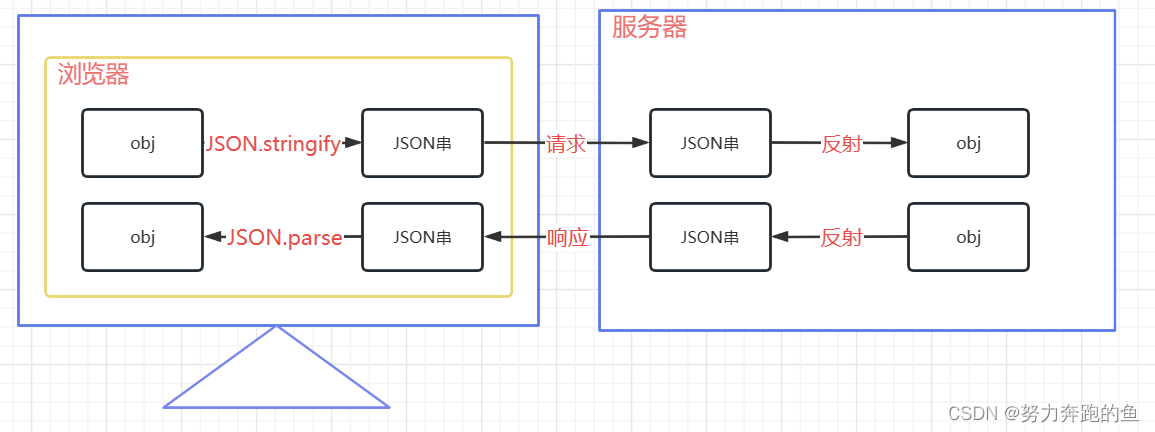
JavaScript-JSON对象
JSON格式 JSON(JavaScript Object Notation, JS对象简谱)是一种轻量级的数据交换格式。它基于ECMAScript(European Computer Manufacturers Association, 欧洲计算机协会的一个子集,采用完全独立于编程语言的文本格式来存储和表示…...

【C语言】自定义类型之---结构体超详解(结构体的定义使用、指针结构体,内存对齐,......代码详解)
目录 前言: 一:结构体 1.1:什么是结构体? 1.2:结构体类型的声明 1.3:结构体变量的定义 1.4:结构体的内存对齐 1.5:结构体传参 二:位段 2.1:位段是什…...

【完美恢复】修复计算机中丢失emp.dll的多个详细方法
最近,在尝试运行某款游戏时,我遭遇了一个令人头痛的问题——“emp.dll文件丢失”。这个错误通常意味着游戏的某个关键文件没有被正确加载或已损坏。以下是我解决问题的步骤和一些心得体会,希望对遇到类似问题的玩家们有所帮助。 emp.dll是一…...

暗黑4可以搬砖吗?暗黑4怎么搬砖 搬砖攻略
暗黑4可以搬砖吗?暗黑4怎么搬砖 搬砖攻略 暗黑破坏神4属于是暴雪旗下一款经典游戏IP,在全世界有着广泛的玩家群体,更是在今年暴雪国服宣布回归之后,吸引了一大批新玩家加入。今天小编就为大家带来暗黑4的详细搬砖教程。 现在我们…...

WLAN技术
冲突域:连接在同一传输线缆上的所有工作站的集合,或者说是同一物理网段上所有节点的集合共同竞争网络资源形成的域叫冲突域。 在OSI模型中,冲突域被看作是第一层的概念,连接同一冲突域的设备有中继器、集线器(hub&…...

维修AB罗克韦尔工控机 PanelView 900 2711-T9C8 SER C 触摸屏人机界面
可视化和 HMI 解决方案可帮助您满足生产力、创新和全球化需求。为电子操作员界面终端、分布式客户端/服务器 HMI 和信息软件提供了一致的外观和感觉。编程工具和高级软件应用程序包括远程访问和数据分析,可加速开发并提高效率。 图形终端 图形终端提供各种尺寸、操…...
)
334_C++_std::bind中使用shared_from_this()
std::bind(&HttpClient::getPwd, shared_from_this(), std::placeholders::_1, std::placeholders::_2);[ HttpClient继承自NetObj,NetObj是父类,NetObj受到std::shared_pt...

【Python】防御性编程入门
1. 前言 防御性编程指的是为了防止代码泄露后被竞品公司窃取技术,使用一种较高级的明文加密编程方式。也可以当做一种带解密性质的时间胶囊,锻炼程序员自己的记忆能力、读代码能力等。 2. 案例分析 2.1 import Import里面可以多取一些喜欢的名字&#…...

无线麦克风哪个品牌音质最好?热门无线麦克风品牌推荐
这段时间短视频行业兴起,很多人都开始尝试步入自媒体,不过想要自己的视频内容更出色、更吸引人,好的音频设备肯定是必不可少的,而麦克风就是其中的一种。麦克风的好坏也将决定了一个视频的质量与完整性等等,如果我们作…...

粒子奇观:用Processing创造宇宙级的动态效果
前言: 👋 今天,我们将一起探索宇宙的奥秘,不是在星空下,而是在Processing的代码世界中。这是我们的第八篇文章,我们将深入粒子系统的神奇领域,学习如何创造出令人惊叹的动态效果。 粒子系统:构建动态世界的基石 🔨 粒子系统是计算机图形学中用于模拟复杂自然现象…...

Filesystem Fragmentation on Modern Storage Systems——论文泛读
TOCS 2023 Paper 论文阅读笔记整理 问题 文件系统碎片是计算机系统随着时间的推移而变慢的主要原因之一。以前认为,碎片化对硬盘驱动器(HDD)等旋转存储设备有害,但不影响固态驱动器(SSD),因为…...

如何同步管理1000个设备的VLAN数据?
什么是VLAN? VLAN,也就是虚拟局域网,是通过为子网提供数据链路连接来抽象出局域网的概念。在企业网中,一个企业级交换机一般是24口或者是48口,连接这些接口的终端在物理上形成一个广播域。广播域过大,就会导…...

【谷粒商城】01-环境准备
1.下载和安装VirtualBox 地址:https://www.virtualbox.org/wiki/Downloads 傻瓜式安装VirtualBox 2.下载和安装Vagrant官方镜像 地址:https://app.vagrantup.com/boxes/search 傻瓜式安装 验证是否安装成功 打开CMD,输入vagrant命令,是否…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
