力扣第99场双周赛题目记录(复盘)
第一题
2578.最小和分割
给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足:
- num1 和 num2 直接连起来,得到 num 各数位的一个排列。
- 换句话说,num1 和 num2 中所有数字出现的次数之和等于 num 中所有数字出现的次数。
- num1 和 num2 可以包含前导 0 。
请你返回 num1 和 num2 可以得到的和的 最小 值。
注意:
- num 保证没有前导 0 。
- num1 和 num2 中数位顺序可以与 num 中数位顺序不同。
示例 1:
输入:num = 4325
输出:59
解释:我们可以将 4325 分割成 num1 = 24 和 num2 = 35 ,和为 59 ,59 是最小和。
示例 2:
输入:num = 687
输出:75
解释:我们可以将 687 分割成 num1 = 68 和 num2 = 7 ,和为最优值 75 。
提示:
- 10 <= num <= 109
思路:
这应该算是个思维题,要把原数拆分成两个数,使得两个数的和最小,那什么情况下最小?比如num=654321,那我们把它变成123+456,就得到最小,即,要满足两个数的位数尽量相同,小数字要在高位。所以我们就可以先获得每一位上的数,将其递增排序,然后将奇数位和偶数位上的数字拼在一起得到两个数,最后得到答案。
代码:
1.C++
class Solution {
public:int splitNum(int num) {vector<int> nums;while(num != 0){nums.push_back(num % 10);num /= 10;}sort(nums.begin(), nums.end());int num1 = 0, num2 = 0, len = nums.size();int i, j;if(len % 2){nums.insert(nums.begin(), 0);len = nums.size();}for(i = 0, j = 1; i < len && j < len; i += 2, j += 2){num1 = num1 * 10 + nums[i];num2 = num2 * 10 + nums[j];}return num1 + num2;}
};
优化一下
class Solution {
public:int splitNum(int num) {string nums = to_string(num);sort(nums.begin(), nums.end());int n[2] = {}, t;for(int i = 0; i < nums.size(); i++){t = i % 2;n[t] = n[t] * 10 + nums[i] - '0';}return n[0] + n[1];}
};

2. Python
class Solution:def splitNum(self, num: int) -> int:nums = sorted(list(str(num)))return int(''.join(nums[::2])) + int(''.join(nums[1::2]))
第二题
2579. 统计染色格子数
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:
- 第一分钟,将 任一 格子染成蓝色。
- 之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。
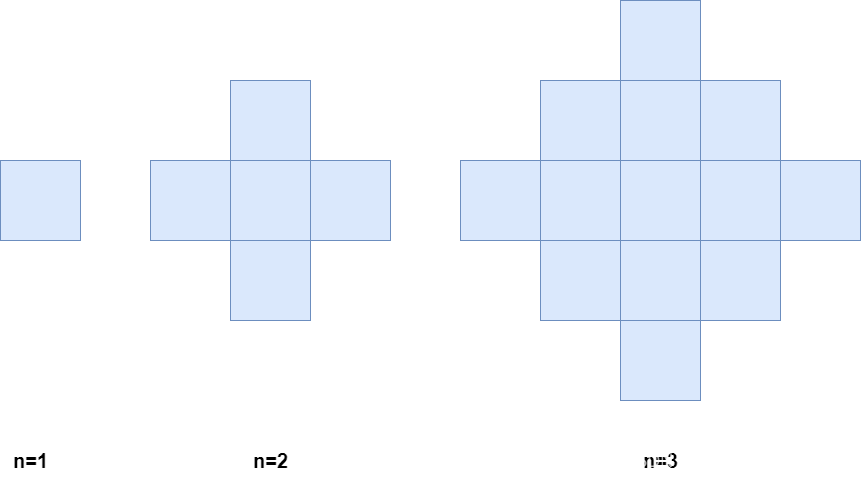
下图分别是 1、2、3 分钟后的网格图。
[https://assets.leetcode.com/uploads/2023/01/10/example-copy-2.png]
请你返回 n 分钟之后 被染色的格子 数目。
示例 1:
输入:n = 1
输出:1
解释:1 分钟后,只有 1 个蓝色的格子,所以返回 1 。
示例 2:
输入:n = 2
输出:5
解释:2 分钟后,有 4 个在边缘的蓝色格子和 1 个在中间的蓝色格子,所以返回 5 。
提示:
- 1 <= n <= 105
思路:
显然,这是一道找数学规律的题,仿佛回到了高中,从第二个开始,可以观察到最中间的一层有 2n - 1个方块,同时往上下分别每层减少两个,也就是2n-1 + (2n-2 + 2n - 4 + … + 1) × 2,所以我们可以模拟这个过程通过累加获得答案,或者直接用等差数列n项和公式并化简一下。
代码:
1.C++模拟
class Solution {
public:long long coloredCells(int n) {long long top = 2 * n, res = top - 1;// cout << top << endl;for(int i = 1; i < top - 1; i += 2){res += 2 * i;}return res;}
};
第三题
2580. 统计将重叠区间合并成组的方案数
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
- 每个区间只属于一个组。
- 两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
- 比方说,区间 [1, 3] 和 [2, 5] 有交集,因为 2 和 3 在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]]
输出:2
解释:
两个区间有交集,所以它们必须在同一个组内。
所以有两种方案:
- 将两个区间都放在第 1 个组中。
- 将两个区间都放在第 2 个组中。
示例 2:
输入:ranges = [[1,3],[10,20],[2,5],[4,8]]
输出:4
解释:
区间 [1,3] 和 [2,5] 有交集,所以它们必须在同一个组中。
同理,区间 [2,5] 和 [4,8] 也有交集,所以它们也必须在同一个组中。
所以总共有 4 种分组方案:
- 所有区间都在第 1 组。
- 所有区间都在第 2 组。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 1 个组中,[10,20] 在第 2 个组中。
- 区间 [1,3] ,[2,5] 和 [4,8] 在第 2 个组中,[10,20] 在第 1 个组中。
提示:
- 1 <= ranges.length <= 105
- ranges[i].length == 2
- 0 <= starti <= endi <= 109
思路:
根据题目描述的提示,我们可以将这个二维数组中的区间划分成两部分,一部分是互相之间有交集的,他们必须在同一个组,另一部分是相对独立的那些区间,它们可以在两个组中自由分配,进一步,假如我们把那部分互相有交集的区间进行合并,变成一个大区间,那不就是相当于一个大区间和n个独立的小区间吗,而这个大区间又可以看做是和n个小区间相独立的一个区间,因此将独立的区间记为res,则答案就是2res。
所以我们先对二维数组排序,然后从前往后依次遍历数组,统计独立的区间个数,有相交的就将其合并。
代码:
1.C++
class Solution {
public:int countWays(vector<vector<int>>& ranges) {sort(ranges.begin(), ranges.end(), [](auto &a, auto &b){return a[0] < b[0];});int right = ranges[0][1], res = 2;const int MOD = 1e9 + 7;// res 记录独立的集合数的放法for(auto pair: ranges){if(pair[0] > right){// 说明pair独立res = (res * 2) % MOD;}// 更新rightright = max(pair[1], right);}return res;}
};
2. Python
class Solution:def countWays(self, ranges: list[list[int]]) -> int:ranges.sort(key=lambda x: x[0])res, right = 1, ranges[0][1]for l, r in ranges:if l > right:res += 1right = max(right, r)return 2 ** res % (10 ** 9 + 7)

总结
第一题考察思维,第二题考察数学推理,第三题考排序+区间组合,感觉还是比较经典的。最后一题一般不看,最多3题选手。
相关文章:

力扣第99场双周赛题目记录(复盘)
第一题 2578.最小和分割 给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足: num1 和 num2 直接连起来,得到 num 各数位的一个排列。 换句话说,num1 和 num2 中所有数字出现的次数之和等于 num 中所…...

spring事务失效原因
一.抛出事务不支持的异常 原理: Spring事务默认支持RuntimeException异常,抛出的异常为RuntimeException异常及其子类异常事务均可生效,而我们日常常见的异常基本都继承自RuntimeException,所以无需指定异常类型事务也能生效。 但…...

pikachu靶场CSRF之TOKEN绕过
简介 Pikachu靶场中的CSRF漏洞环节里面有一关CSRF TOKEN,这个关卡和其余关卡稍微有点不一样,因为表单里面存在一个刷新就会变化的token,那么这个token是否能绕过呢?接下来我们来仔细分析分析 实战过程 简单尝试 先利用任意一个…...
Windows中配置docker没有hyper-v功能解决方案
👨 作者简介:大家好,我是Taro,前端领域创作者 ✒️ 个人主页:唐璜Taro 🚀 支持我:点赞👍📝 评论 ⭐️收藏 文章目录前言解决步骤:1.新建文档2. 另存为3. 功能…...
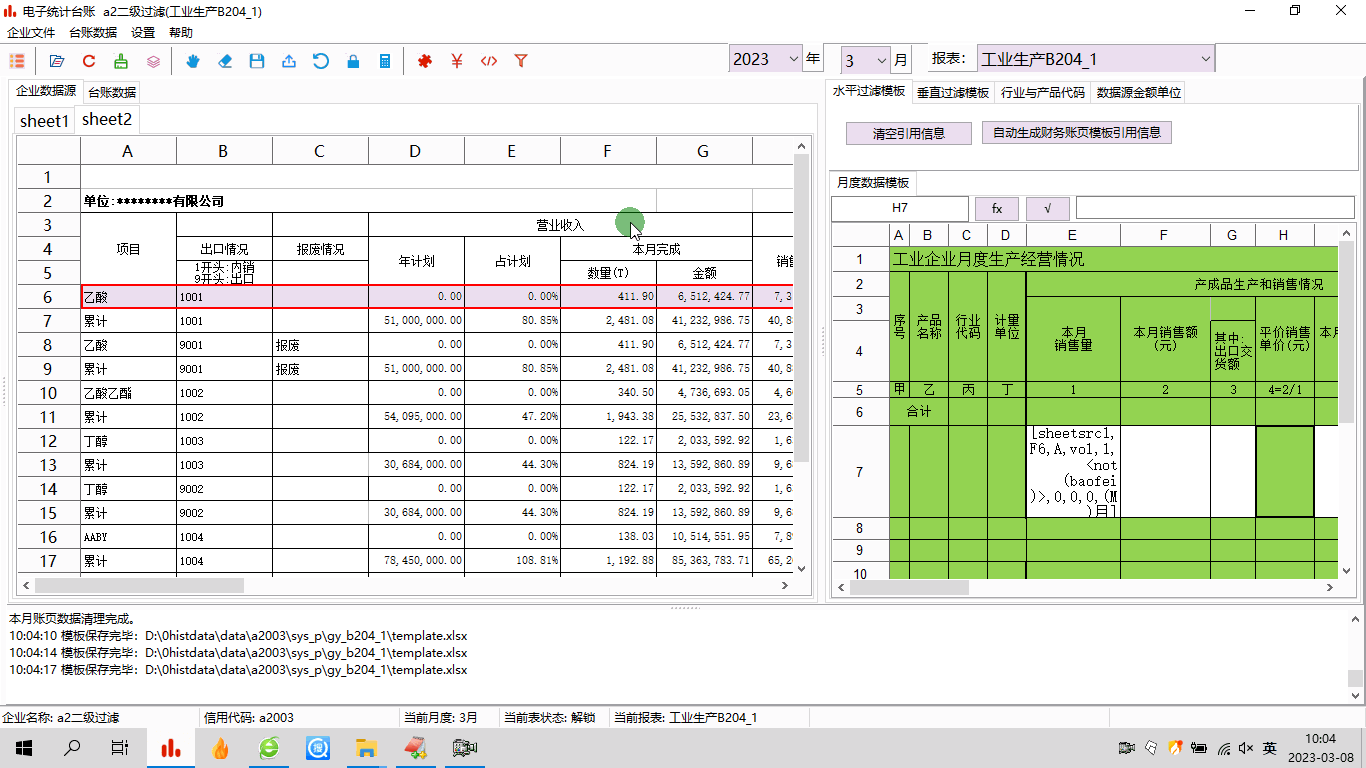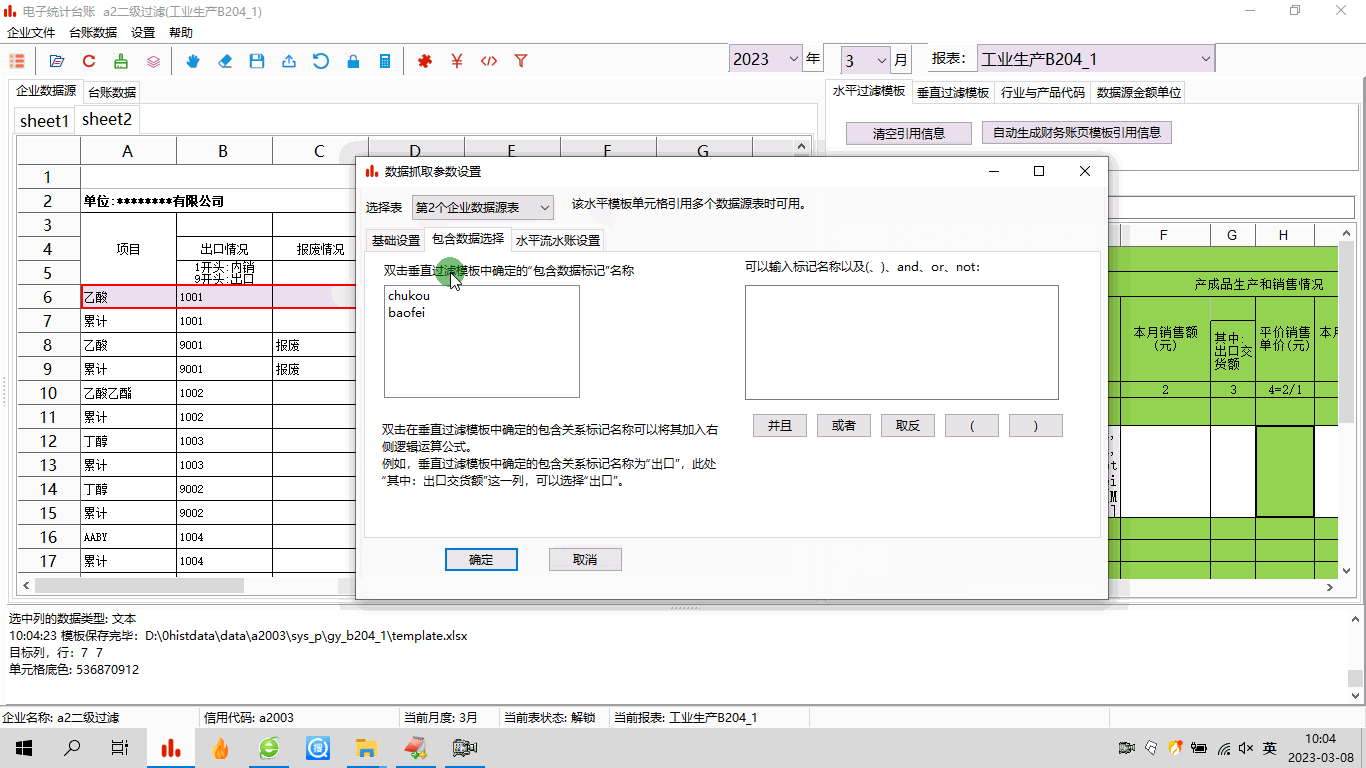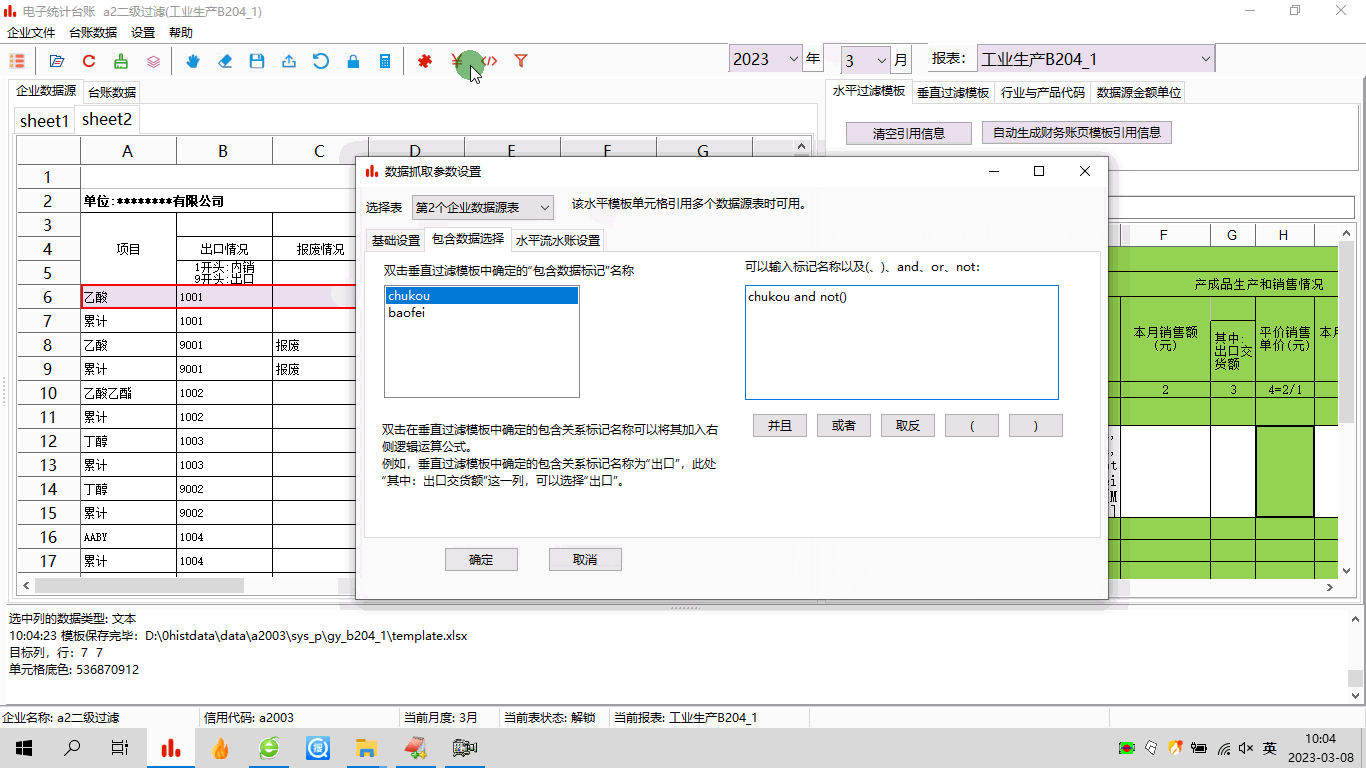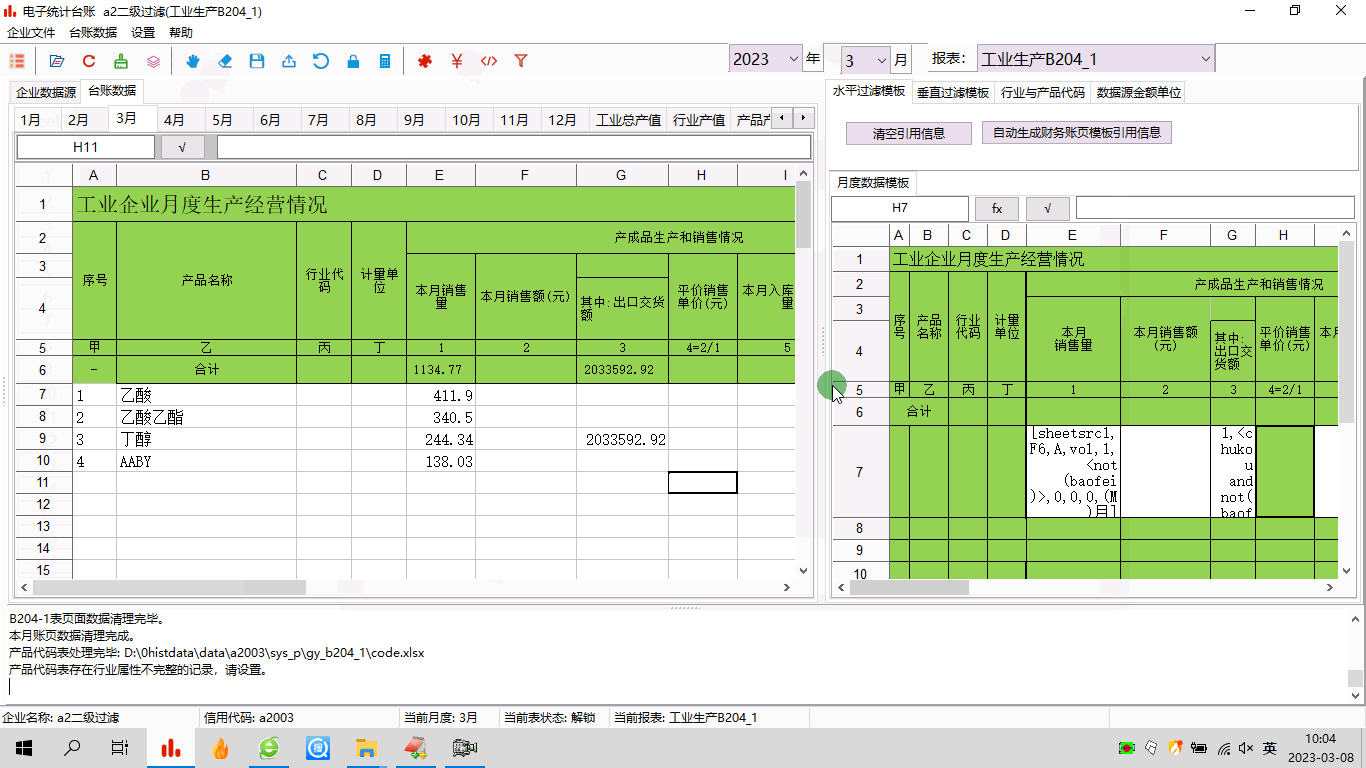
电子台账:模板制作之五——二级过滤与多条件组合
1 前言工作中,经常会遇到很复杂的数据,比如内销产品和出口产品、正常产品和报废产品都混在一块儿。电子台账中,需要把这些数据都区分开,分别汇总。这种情况,可以用台账软件的二级过滤功能来处理,实际上就是…...

Kaldi Data preparation
链接:GitHub - nessessence/Kaldi_ASR_Tutorial: speech recognition using Kaldi framework Lets start with formatting data. We will randomly split wave files into test and train dataset(set the ratio as you want). Create a directory data and,then t…...

libevent 学习笔记
一、参考 libevent Libevent深入浅出 - 《Libevent 深入浅出》 - 书栈网 BookStack libevent 之 event config的相关函数介绍_event_config_new_yldfree的博客-CSDN博客 Libevent之evbuffer详解_有时需要偏执狂的博客-CSDN博客 二、libevent概述 libevent 就是将网络、I…...
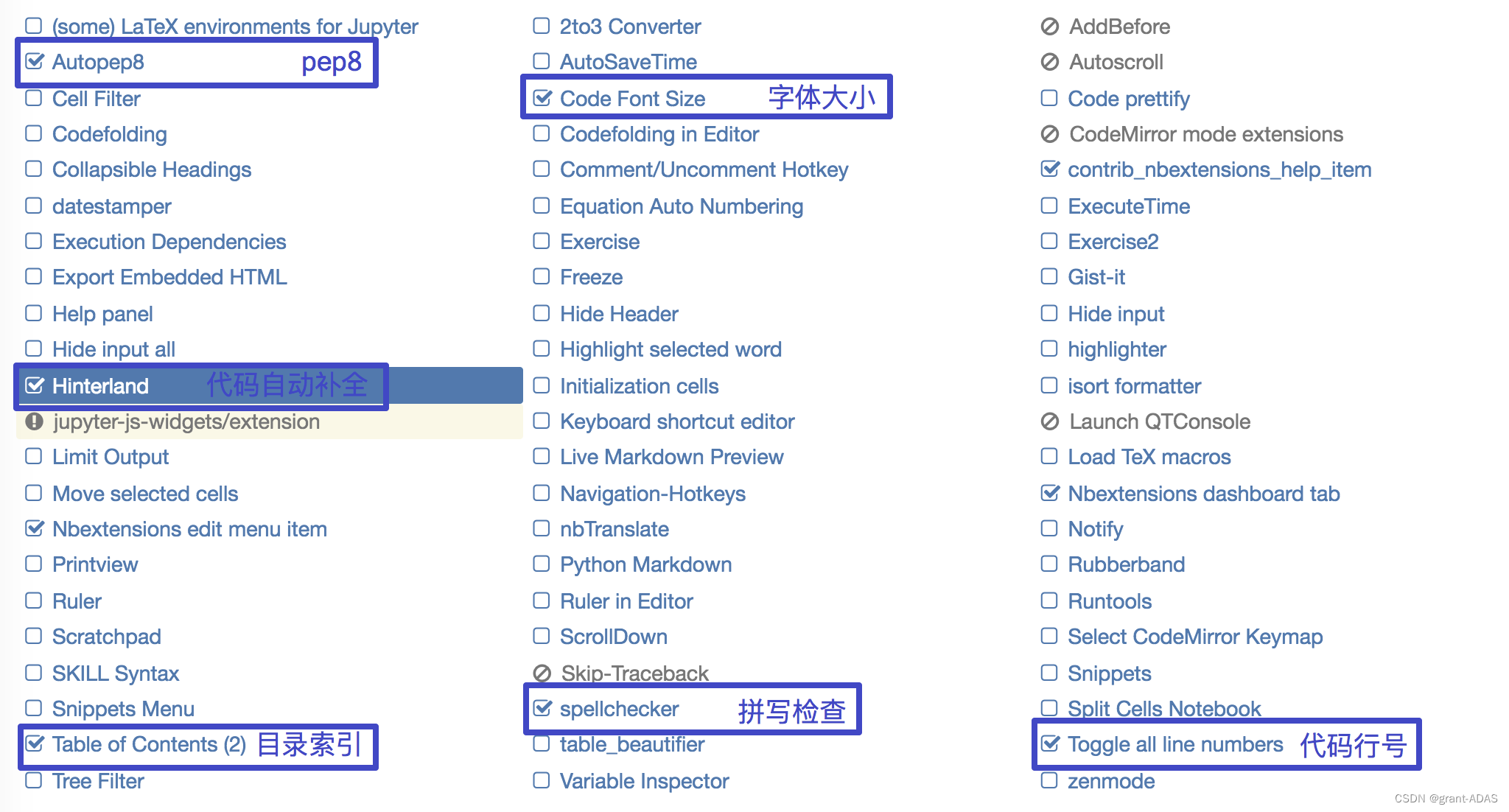
jupyter的使用
1.安装 安装过程看这篇记录。 安装 2.如何启动 环境搭建好后,本机输⼊jupyter notebook命令,会⾃动弹出浏览器窗⼝打开 Jupyter Notebook # 进⼊虚拟环境 workon ai(这个是虚拟环境的名称) # 输⼊命令 jupyter notebook本地notebook的默认URL为&…...

中级数据开发工程师养成计
目标 工作之后就很少时间用来沉淀知识了,难得用空闲时间沉淀一下自己。 成为一名中级数据开发工程师。偏向于数据仓库,数据治理方向。 整体排期 1 hive 2 hadoop 3 flink 4 spark 5 闲杂工具 kafka maxwell cancal 6 数据建模(偏向于kimbo…...
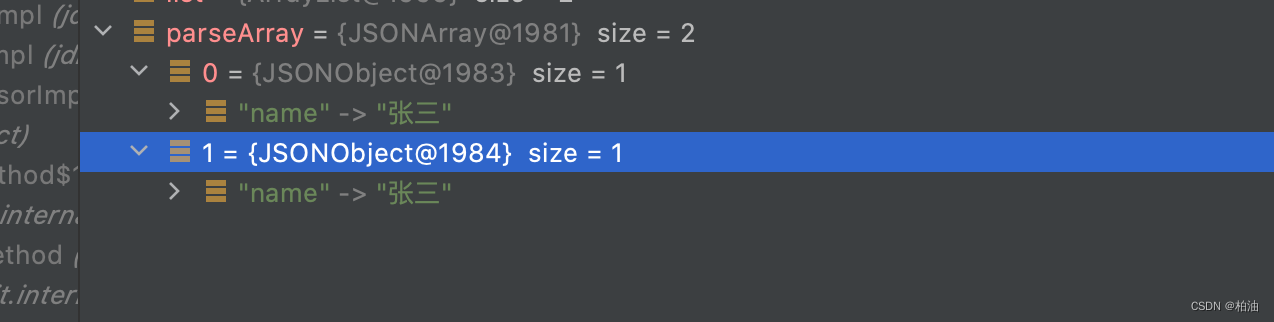
fastjson 返回 $ref 数据
文章目录问题描述:1、重复引用:2、循环引用:原因分析:1、重复引用:2、循环引用:反序列化:1、开启引用检测:2、关闭引用检测:小结:问题描述: 问题…...

Zookeeper特性和节点数据类型详解
什么是ZK? zk,分布式应用协调框架,Apache Hadoop的一个子项目,解决分布式应用中遇到的数据管理问题。 可以理解为存储少量数据基于内存的数据库。两大核心:文件系统存储结构 和 监听通知机制。 文件系统存储结构 文件目录以 / …...

Java代码是如何被CPU狂飙起来的?
无论是刚刚入门Java的新手还是已经工作了的老司机,恐怕都不容易把Java代码如何一步步被CPU执行起来这个问题完全讲清楚。但是对于一个Java程序员来说写了那么久的代码,我们总要搞清楚自己写的Java代码到底是怎么运行起来的。另外在求职面试的时候这个问题…...
Dynamics365安装失败解决及注册编写
一、修改错误昨天登录报错今天开始返回我之前设置的断点开始重新配置,Reporing Services配置完成后发现dynamics365还是下载失败之后下载了一上午dynamics365就一直卡在最后的界面进度条不动索性我直接把所有环境都卸载了 连同虚拟机卸载重装终于在下午的时候dynami…...

Kafka 集群参数
Kafka 集群参数Broker 端参数存储配置ZooKeeper 配置Broker 连接配置Topic 管理配置数据留存配置Topic 级别参数JVM 参数操作系统参数重要的配置 : Broker 端参数,主题级别的参数、JVM 端参数、操作系统级别的参数 Broker 端参数 存储配置 log.dirs:指…...

等保2.0与1.0 测评要求的变化
No.1标准内容增加了 标准内容上最大的变化就是将安全要求分为了安全通用要求和扩展要求。首先,安全通用要求部分已对1.0标准的内容进行了优化,删除或修订了过时的要求项,新增了对新型网络攻击行为防护和个人信息保护等方面的新要求。其次&am…...
nodejs学习巩固笔记-nodejs基础,Node.js 高级编程(核心模块、模块加载机制)
目录Nodejs 基础大前端开发过程中的必备技能nodejs 的架构为什么是 NodejsNodejs 异步 IONodejs 事件驱动架构全局对象全局变量之 process核心模块核心模块 - path全局变量之 Buffer创建 bufferBuffer 实例方法Buffer 静态方法Buffer-split 实现核心模块之FS模块文件操作 APImd…...
-3 || 附:创新点、创新思想和技术路线总结)
2023年春【移动计算技术】文献精读(二)-3 || 附:创新点、创新思想和技术路线总结
榜样的力量是无穷的! 🎯作者主页:追光者♂ 🌸个人简介:2022年CSDN博客之星人工智能领域TOP4🌟、阿里云社区专家博主🏅 CSDN-人工智能领域新星创作者🏆 【无限进步,一起追光!】 🍎欢迎点赞👍 收藏⭐ 留言📝 🌿本篇,仅接着上两篇,为【移动计算技术】…...

企业新闻稿的格式和要求是什么?如何写好新闻稿?
新闻稿是企业自己撰写给媒体的新闻素材,媒体采纳你的稿件后就可以传播到更多的大众面前。 所以企业新闻稿的撰写一方面要让媒体认可,另外一方面是让用户认可你的品牌或是产品。 企业新闻稿的格式和要求是什么?如何写好新闻稿?今…...

String类的底层原理和版本演变
1 String类的底层演变(1) JDK8以及之前版本 (2)JDK9以及之后版本 javaJDK8的字符串存储在char类型的数组里面,在java中,一个char类型占两个字节。但是很多时候,一个字符只需要一个字节就可存储&…...

软考高级信息系统项目管理师系列之二十三:项目采购管理
软考高级信息系统项目管理师系列之二十三:项目采购管理 一、项目采购管理内容整理二、项目采购管理1.采购的定义2.项目采购管理3.战略合作管理三、规划采购1.供应商管理2.采购需求与计划3.规划采购的输入、输出、工具和技术四、实施采购1.采购合同知识2.实施采购的输入、输出、…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
