CCF PTA 2022年11月C++大富翁游戏
【问题描述】
小明很喜欢玩大富翁游戏,这个游戏的规则如下: 1、游戏地图是有 N 个格子,分别编号从 1 到 N。玩家一开始位于 1 号格子。 2、地图的每个格子上都有事件,事件有以下两种类型: A)罚款 x 枚金币。如果 x 为负数,则表示获得-x 枚金币; B)强制前进 y 个格子(输入数据保证,前进后不会越过 N 号格子)。 3、游戏开始时首先触发 1 号格子的事件,然后开始玩家回合。 4、玩家每回合可以选择前进 1 或 2 个格子(不可以不移动,不可以越过 N 号格子),之后触发停 留的格子的事件。 4.1、如果触发的是 A 类事件,进行罚款。若罚款后金币数小于 0,则游戏失败,否则继续下一个 回合; 4.2、如果触发的是 B 类事件,强行前进。若强行前进后所在的格子为 A 类事件,则按照 4.1 的规 则触发 A 类事件;若为 B 类事件,则当前回合不再触发 B 类事件。 5、如果玩家回合结束时,处在 N 号格子,且金币数大于等于 0,则游戏胜利。 可以看出,如果玩家一开始有足够多的金币,总是能够通过合理选择前进方案获得胜利。小明想 知道,一开始最少需要多少金币,才有可能取得游戏胜利?
【输入描述】
第一行给出正整数 N,为地图的长度。 接下来 N 行,分别描述从 1 到 N 号格子的事件:A x 或者 B y。
【输出描述】
一个整数,要取得游戏胜利,最少需要的金币数。
【输入样例】
7
A -2
A 3
B 1
A 2
A 4
A 2
A 0
【输出样例】
2
【数据规模】
100%数据满足2 ≤ 𝑁 ≤ 128,−8 ≤ 𝑥 ≤ 8,0 ≤ 𝑦 ≤ 2。
【题解】
本题关键点:动态规划,代码如下。
#include <iostream>
using namespace std;
//动态规划,由最后一个格子依次往前计算每个格子所需的最少金币
//玩家在n+1号格子,且触发完事件,面临回合选择时,最少持有map[n].cost个金币const int MAX_CELL=128;
struct cell{char type;int xy;int cost;
};
cell map[MAX_CELL];
int main(){int N=0;cin>>N;for(int n=0;n<N;n++){cin>>map[n].type>>map[n].xy;}map[N-1].cost=0;//动态规划 for(int n=N-2;n>=0;n--){int cost=0;//求cost:n+1号格子最少需要多少金币for(int d=1;d<=2 && n+d<N;d++){int ncost=0;if(map[n+d].type=='A'){ncost=map[n+d].xy+map[n+d].cost;}else{int nd = n+d+map[n+d].xy;if(map[nd].type=='A'){ncost=map[nd].xy+map[nd].cost;}else{ncost=map[nd].cost;}}if(d==1 || cost>ncost)cost=ncost;}if(cost<0)cost=0;map[n].cost=cost; }int total=0;//求total:游戏开始时最少需要多少金币if(map[0].type=='A'){total=map[0].xy+map[0].cost;}else{int nd=map[0].xy;if(map[nd].type=='A'){total=map[nd].xy+map[nd].cost;}else{total=map[nd].cost;}}if(total<0)total=0;cout<<total<<endl; return 0;
}相关文章:

CCF PTA 2022年11月C++大富翁游戏
【问题描述】 小明很喜欢玩大富翁游戏,这个游戏的规则如下: 1、游戏地图是有 N 个格子,分别编号从 1 到 N。玩家一开始位于 1 号格子。 2、地图的每个格子上都有事件,事件有以下两种类型: A)罚款 x 枚金币…...

React获取form表单值的N种方式
Ref模式(非受控模式) 非钩子模式 1.createRef()方式 js: userNameElcreateRef() <input type"text" name"userName" ref{this.userNameEl} /> 获取值的方式: this.userNameEl.current.value2.refs(废弃) js: con…...
Apache Knox 2.0.0使用
目录 介绍 使用 gateway-site.xml users.ldif my_hdfs.xml my_yarn.xml 其它 介绍 The Apache Knox Gateway is a system that provides a single point of authentication and access for Apache Hadoop services in a cluster. The goal is to simplify Hadoop securit…...

Tomcat 内核详解 - Web服务器机制
详细介绍 Apache Tomcat 是一个开源的Web服务器和Servlet容器,它实现了Java Servlet、JavaServer Pages (JSP) 和WebSocket规范。Tomcat的核心设计围绕着几个关键组件,它们共同构成了处理HTTP请求、管理Web应用部署和执行Servlet逻辑的基础架构。 Apac…...

几个人脸库对于面部动作识别的功能比较
经粗略研究,insightface只能识别面部特征点的位置,根据这些位置不能直接推出一个人是否在睡觉。 OpenFace 是一个高级的面部行为分析工具,它能够识别和分析多种面部动作单位(Facial Action Coding System, FACS),这些动作单位是根据面部肌肉活动定义的。每个动作单位(A…...
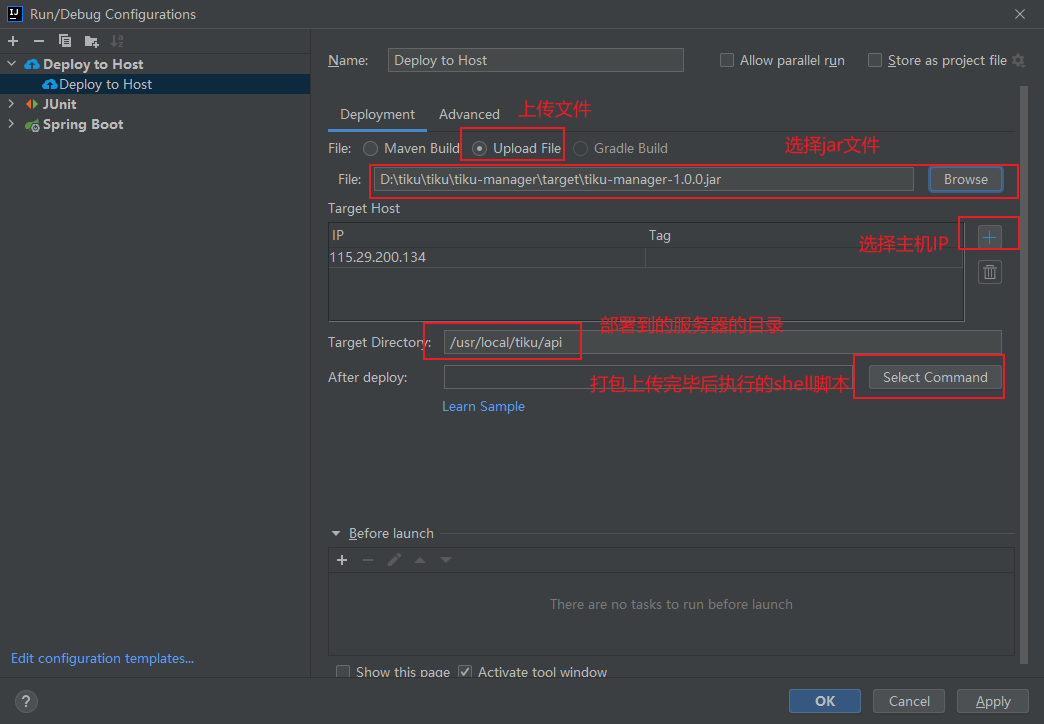
IDEA 使用Alibaba Cloud Toolkit 实现远程 自动部署
安装插件 maven方式部署 配置服务器主机信息 配置发布到主机 单击Select 单击run 就可以将选择module的jar文件上传到服务器的指定位置了 Alibaba Cloud Toolkit 上传文件的方式部署...

蓝桥杯备战15.完全二叉树的权值
P8681 [蓝桥杯 2019 省 AB] 完全二叉树的权值 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) #include<bits/stdc.h> using namespace std; #define endl \n #define int long long const int N 2e510; int a[N]; signed main() {std::ios::sync_with_stdio(0),cin.ti…...

【前端】LayUI监听事件汇总
一、监听单选按钮事件 点击资源类型单选按钮时,请求后台接口,把接口返回的内容追加到选择资源下拉框内 HTML <div class"layui-form-item"><label class"layui-form-label">资源类型:</label><d…...
)
【多电压流程 Multivoltage Flow】- 5.特定工具使用建议(1.VCS NLP VC LP)
本章提供了关于使用Synopsys工具进行低功耗设计和分析的信息。它包含以下部分: • 使用VCS NLP和VC LP进行多电压验证 • 使用Design Compiler进行逻辑综合 • 使用IC Compiler进行设计规划 • 使用IC Compiler进行物理实现 • 使用IC Compiler II和Fusion Compiler进行物…...
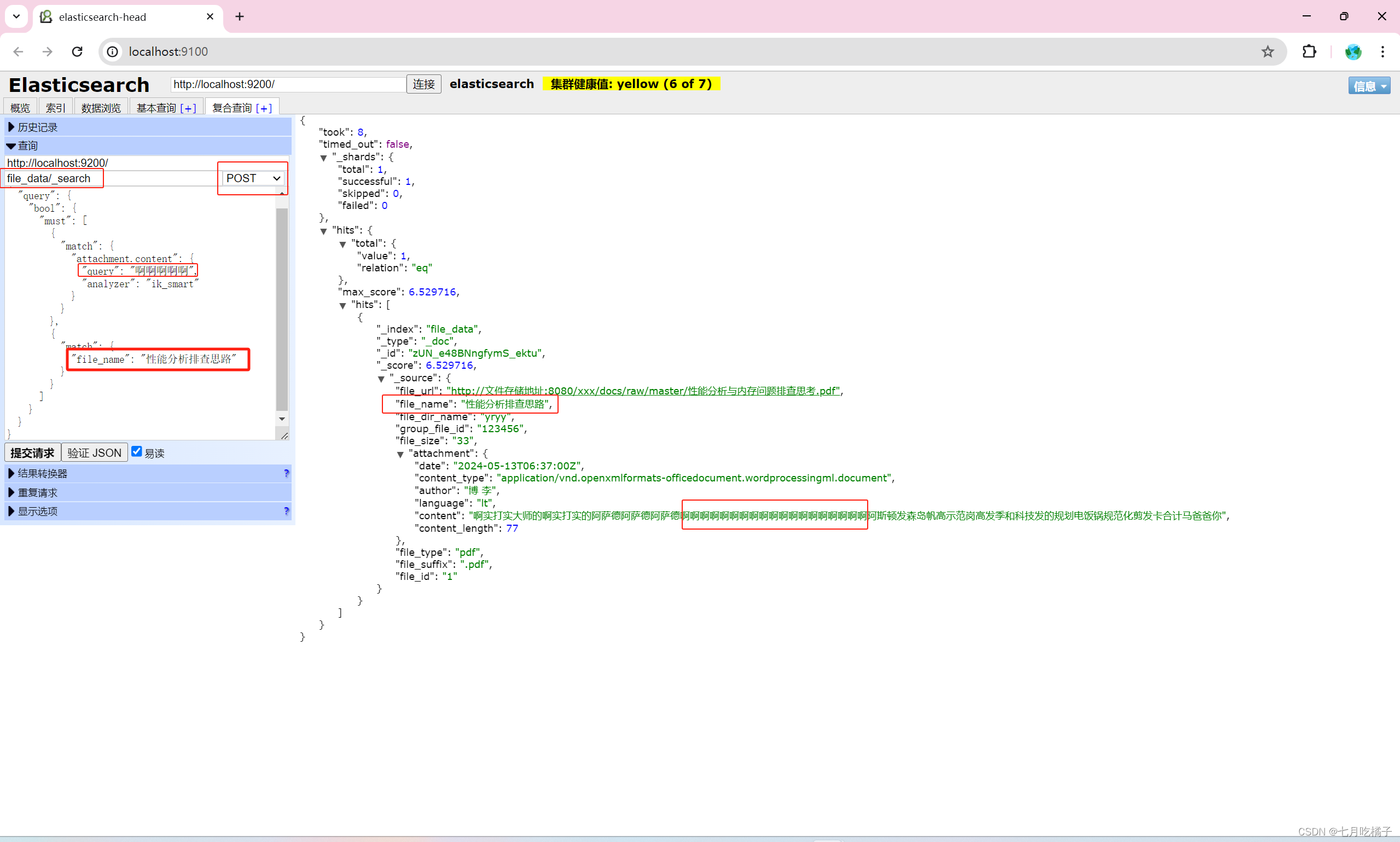
Elasticsearch 实现word、pdf、txt、excel文档内容快速检索(保姆级教程)
本文主要讲解ES如何从提取文档中提取内容(word、pdf、txt、excel等文件类型),实现快速检索文档内容实现。 特别说明一下,为什么用7.10.0版本,因为在项目中除了精确匹配的要求,也会有模糊查询(关…...

[初学rust] 04_rust复合类型
rust复合类型 字符串 由于rust的字符串元素类型是u8(1字节),但是字符类型是unicode(4字节) 索引不能像C那样读取又由于String类型和&str类型都是utf-8编码,中文占3字节切片可能会导致崩溃 slice(切片) 切片就是对String类型中的一部分的引用,它…...

什么是Zoho CRM客户关系系统管理?
以客户为中心的商业时代,卓越的客户体验已成为企业持续增长与成功的关键,为了在这场激烈的市场竞争中脱颖而出,企业需要一套强大、灵活且智能的客户关系管理系统——Zoho CRM应运而生,它不仅是管理客户信息的工具箱,更是驱动业务增…...

青岛东软载波子公司东软载波微电子授权世强硬创代理,出货量累计超20亿颗
凭借业内独特的互联网推新模式,世强先进(深圳)科技股份有限公司(下称“世强先进”) 获得本土工业MCU企业——上海东软载波微电子有限公司(下称“东软载波微电子”,英文:essemi&#…...
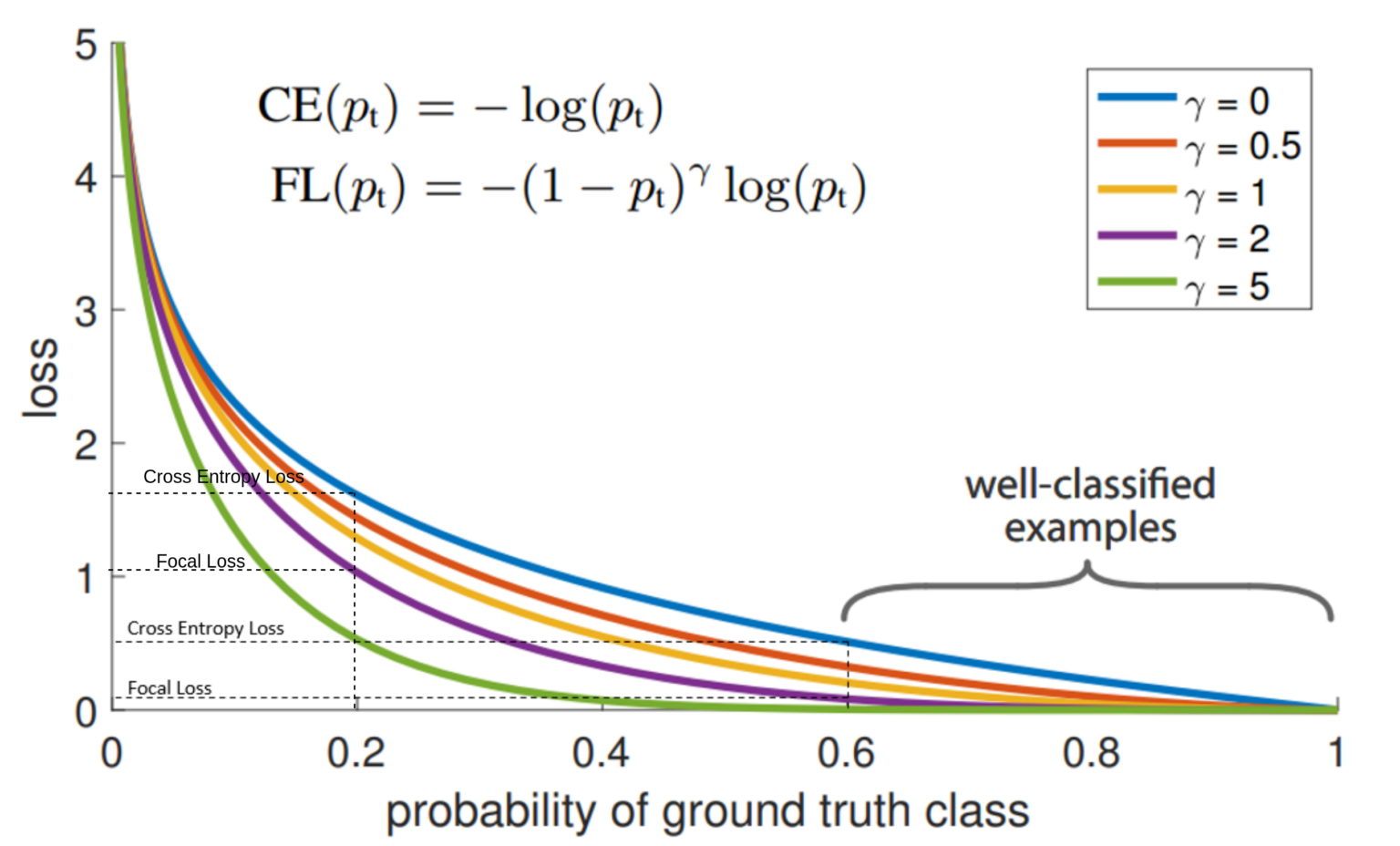
YOLO损失函数——SIoU和Focal Lossr损失函数解析
1. 概述 YOLO(You Only Look Once) 系列模型以其实时目标检测能力而闻名,其有效性在很大程度上归功于其专门设计的损失函数。在本文中,这里将深入探讨YOLO演进中不可或缺的各种YOLO损失函数,并重点介绍它们在PyTorch中…...

C++:编程世界的永恒之石
在编程的广袤领域中,C犹如一块永恒的基石,历经岁月的洗礼,依旧坚固而璀璨。它的深厚底蕴、强大功能和广泛的应用领域,使其成为无数程序员心中的信仰与追求。 一、C:历史与传承的交汇点 C的历史可追溯到上世纪80年代&…...

线上3D博物馆搭建简单吗?有何优势?有哪些应用场景?
随着科技的飞速发展,传统的博物馆参观方式正在经历一场前所未有的变革,在科技的“加持”下,不少博物馆凭借强大的技术、创意和美学实践,频频“出圈”,线上3D博物馆逐渐崛起,这不仅丰富了人们的文化体验&…...

Rust 语言的“命名空间” —— mod
在Rust中,虽然没有像C中的namespace这样的显式关键字,但是Rust通过模块(mod)系统提供了一种类似命名空间的功能。模块允许你将相关的代码组织在一起,并可以通过pub关键字来控制哪些项(如函数、结构体、枚举…...

加速科技突破2.7G高速数据接口测试技术
随着显示面板分辨率的不断提升,显示驱动芯片(DDIC)的数据接口传输速率越来越高,MIPI、LVDS/mLVDS、HDMI等高速数据接口在DDIC上广泛应用。为满足高速数据接口的ATE测试需求,作为国内少数拥有完全自研的LCD Driver测试解…...

从0开始搭建一个react项目 第一 二 三天
从0开始搭建一个react项目 今天接到一个任务让我把原来用ext.js写的前端换成react写的,我好慌的,因为我就是一个小白,之前只做过简单的二次开发功能。唉,我只是一个领着微薄薪水的小实习生,为什么要有这个任务&#x…...
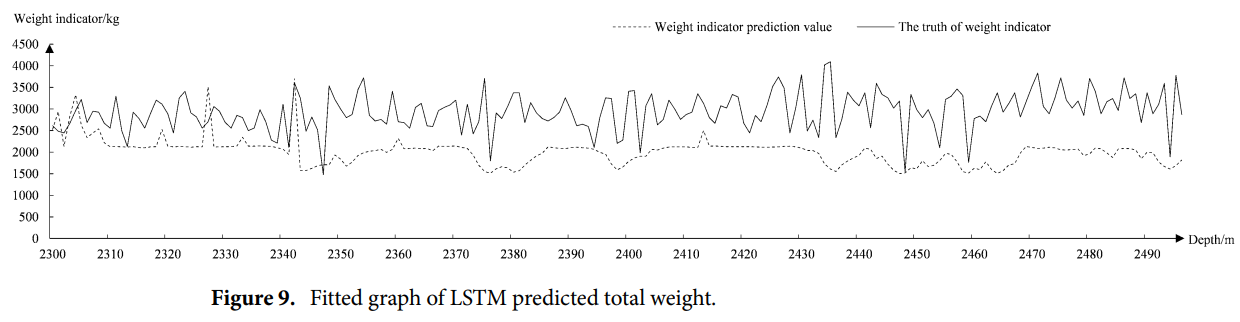
LSTM与GAN创新结合!模型性能起飞,准确率超98%
今天来聊一个深度学习领域非常具有创新性的研究方向:LSTM结合GAN。 LSTM擅长处理和记忆长期的时间依赖关系,而GAN可以学习复杂的数据分布并生成逼真的数据样本。通过充分结合两者的优势,我们可以增强模型对复杂数据的处理能力,提…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
