图和网络笔记
1. A X = 0 AX=0 AX=0
一个图可以由节点和边组成,假设我们有一个节点notes :n=4,边edges:m=5的有向图,表示如下

- 通过以上电路图可以得到关联矩阵(incident matrix),我们定义边,开始端用-1表示,结束端用1表示,用行表示边,用列表示节点。可得如下
比如edge1是由从节点1出发,到节点2 ,用行向量表示可得
[ − 1 1 0 0 ] ⇒ e d g e 1 (1) \begin{bmatrix}-1&1&0&0\end{bmatrix}\Rightarrow edge1\tag{1} [−1100]⇒edge1(1) - 所以矩阵A根据上图可得如下:
A = [ − 1 1 0 0 0 − 1 1 0 − 1 0 1 0 − 1 0 0 1 0 0 − 1 1 ] (2) A=\begin{bmatrix}-1& 1& 0& 0\\\\ 0 &-1& 1& 0\\\\ -1& 0& 1& 0\\\\ -1& 0& 0& 1\\\\ 0 & 0&-1& 1\end{bmatrix}\tag{2} A= −10−1−101−10000110−100011 (2)-
我们可以看到由边1,2,3组成一个子图,那么看看由1,2,3组成的矩阵表示如下:
[ − 1 1 0 0 0 − 1 1 0 − 1 0 1 0 ] ⇒ r o w 1 + r o w 2 = r o w 3 (3) \begin{bmatrix}-1& 1& 0& 0\\\\ 0 &-1& 1& 0\\\\ -1& 0& 1& 0 \end{bmatrix}\Rightarrow row_1+row_2=row_3\tag{3} −10−11−10011000 ⇒row1+row2=row3(3)

也就是说,如果在矩阵中3行能达到等式关系,可以等效与在图上形成一个子图。
- 那么矩阵A的零空间代表什么呢?我们将AX=0 用列的形式表示如下:
A X = [ − 1 1 0 0 0 − 1 1 0 − 1 0 1 0 − 1 0 0 1 0 0 − 1 1 ] [ x 1 x 2 x 3 x 4 ] = [ x 2 − x 1 x 3 − x 2 x 3 − x 1 x 4 − x 3 ] (4) AX=\begin{bmatrix}-1& 1& 0& 0\\\\ 0 &-1& 1& 0\\\\ -1& 0& 1& 0\\\\ -1& 0& 0& 1\\\\ 0 & 0&-1& 1\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\x_3\\\\x_4\end{bmatrix}=\begin{bmatrix}x_2-x_1\\\\x_3-x_2\\\\x_3-x_1\\\\x_4-x_3\end{bmatrix}\tag{4} AX= −10−1−101−10000110−100011 x1x2x3x4 = x2−x1x3−x2x3−x1x4−x3 (4)
A X = [ − 1 0 − 1 − 1 0 ] x 1 + [ 1 − 1 0 0 0 ] x 2 + [ 0 1 1 0 − 1 ] x 3 + [ 0 0 0 1 1 ] x 4 (5) AX=\begin{bmatrix}-1\\\\0\\\\-1\\\\-1\\\\0\end{bmatrix}x_1+\begin{bmatrix}1\\\\-1\\\\0\\\\0\\\\0\end{bmatrix}x_2+\begin{bmatrix}0\\\\1\\\\1\\\\0\\\\-1\end{bmatrix}x_3+\begin{bmatrix}0\\\\0\\\\0\\\\1\\\\1\end{bmatrix}x_4\tag{5} AX= −10−1−10 x1+ 1−1000 x2+ 0110−1 x3+ 00011 x4(5)
- 那么矩阵A的零空间代表什么呢?我们将AX=0 用列的形式表示如下:
-
- AX=0的零空间X表示的是列向量的线性组合。X的物理意义表示的每个节点的电势值[potential at the node ],那么 x 2 − x 1 x_2-x_1 x2−x1表示的是edge1的电势差,那什么时候可以保证电势差为0呢,那只有每个结点的电势相同即可,所以可以得到解如下,所以 dim N ( A ) = 1 , R a n k ( A ) = 4 − 1 = 3 N(A)=1,Rank(A)=4-1=3 N(A)=1,Rank(A)=4−1=3
X = c [ 1 1 1 1 ] (6) X=c\begin{bmatrix}1\\\\1\\\\1\\\\1\end{bmatrix}\tag{6} X=c 1111 (6)
2. A T Y = 0 A^TY=0 ATY=0
- 矩阵表示形式如下, dim N ( A T ) = m − r ( A T ) = 5 − 3 = 2 N(A^T)=m-r(A^T)=5-3=2 N(AT)=m−r(AT)=5−3=2,物理上表示 y 1 … y 5 y_1\dots y_5 y1…y5为每个边edge上的电流大小:
A T Y = [ − 1 0 − 1 − 1 0 1 − 1 0 0 0 0 1 1 0 − 1 0 0 0 1 1 ] [ y 1 y 2 y 3 y 4 y 5 ] = [ − y 1 − y 3 − y 4 y 1 − y 2 y 2 + y 3 − y 5 y 4 + y 5 ] = [ 0 0 0 0 ] (7) A^TY=\begin{bmatrix}-1& 0& -1& -1&0\\\\ 1& -1& 0& 0&0\\\\ 0& 1& 1& 0&-1\\\\ 0& 0& 0& 1&1 \end{bmatrix}\begin{bmatrix}y_1\\\\y_2\\\\y_3\\\\y_4\\\\y_5\end{bmatrix}=\begin{bmatrix}-y_1-y_3-y_4\\\\y_1-y_2\\\\y_2+y_3-y_5\\\\y_4+y_5\end{bmatrix}=\begin{bmatrix}0\\\\0\\\\0\\\\0\end{bmatrix}\tag{7} ATY= −11000−110−1010−100100−11 y1y2y3y4y5 = −y1−y3−y4y1−y2y2+y3−y5y4+y5 = 0000 (7) - 函数物理意义:
− y 1 − y 3 − y 4 = 0 ⇒ y 1 + y 3 = − y 4 (8) -y_1-y_3-y_4=0\Rightarrow y_1+y_3=-y_4\tag{8} −y1−y3−y4=0⇒y1+y3=−y4(8)
表示的对于节点1来说,流入的电流为 − y 4 -y_4 −y4,流出的电流为 y 1 + y 3 y_1+y_3 y1+y3,所以可以得到基尔霍夫电流定律,流入节点电流和等于流出节点的电流和

- N( A T A^T AT)=m-r=5-3=2,我们看由1,2,3组成的节点环1,如果想成为闭环,可以得到如下:
y 1 + y 2 − y 3 = 0 (9) y_1+y_2-y_3=0\tag{9} y1+y2−y3=0(9) - A T Y = 0 A^TY=0 ATY=0的特解中当 y 1 = 1 , y 2 = 1 , y 3 = − 1 , y 4 = 0 , y 5 = 0 y_1=1,y_2=1,y_3=-1,y_4=0,y_5=0 y1=1,y2=1,y3=−1,y4=0,y5=0,表示 L o o p 123 Loop_{123} Loop123
- A T Y = 0 A^TY=0 ATY=0的特解中当 y 1 = 0 , y 2 = 0 , y 3 = 1 , y 4 = − 1 , y 5 = 1 y_1=0,y_2=0,y_3=1,y_4=-1,y_5=1 y1=0,y2=0,y3=1,y4=−1,y5=1,表示 L o o p 345 Loop_{345} Loop345
- A T Y = 0 A^TY=0 ATY=0的特解中当 y 1 = 1 , y 2 = 1 , y 3 = 0 , y 4 = − 1 , y 5 = 1 y_1=1,y_2=1,y_3=0,y_4=-1,y_5=1 y1=1,y2=1,y3=0,y4=−1,y5=1,表示 L o o p 1234 Loop_{1234} Loop1234
- 线性无关组表示不形成环时的边组合。这样可以看出来矩阵和图的对应关系。很直观。
- 矩阵的相关就是表示图形中的环,矩阵的不相关就是表示不成环,形成树。


- 矩阵的秩和图之间的关系
- D i m { N ( A T ) } Dim \{N(A^T)\} Dim{N(AT)}=#loops;
- m=#edges;
- r=n-1,节点的数量-1
D i m { N ( A T ) } = m − r (10) Dim \{N(A^T)\}= m-r\tag{10} Dim{N(AT)}=m−r(10)
综上所述,可以得到如下
# n o d e s − # e d g e s + # L o o p s = 1 (11) \#{nodes}-\#{edges}+\#{Loops}=1\tag{11} #nodes−#edges+#Loops=1(11)
3. A X = 0 AX=0 AX=0和 A T Y = 0 A^TY=0 ATY=0的关系
-
在 A X = 0 AX=0 AX=0 的方程中,我们定义每个边两端的电势差E
E = A X (12) E=AX\tag{12} E=AX(12) -
在 A T Y = 0 A^TY=0 ATY=0的方程中,我们定义每个边中的电流为y,通过欧姆定理,定义电势差E,和常数C,电流Y之间的关系如下:
Y = C E (13) Y=CE\tag{13} Y=CE(13) -
电流方程如下:
A T Y = 0 (14) A^TY=0\tag{14} ATY=0(14) -
将方程12,13 代入到方程14中可得如下:
A T C A X = 0 (15) A^TCAX=0\tag{15} ATCAX=0(15) -
我们定义外部电流从原来的0变为f,整理公式15可得平衡方程,并且 A T C A A^TCA ATCA对称:
A T C A X = f (16) A^TCAX=f\tag{16} ATCAX=f(16)
相关文章:

图和网络笔记
文章目录 1. A X 0 AX0 AX02. A T Y 0 A^TY0 ATY03. A X 0 AX0 AX0和 A T Y 0 A^TY0 ATY0的关系 1. A X 0 AX0 AX0 一个图可以由节点和边组成,假设我们有一个节点notes :n4,边edges:m5的有向图,表示如下 通过以上电路…...

请求外部系统报错
报错信息: nested exception is com.google.common.util.concurrent.ExecutionError: java.lang.NoSuchMethodError: com.google.common.net.HostAndPort.getHostText()Ljava/lang/String; 在网上看了好几篇文章,和我的都不符合。 后面自己发现是我的系…...

电路板维修【四】
【开关电源输出电压偏低不稳,用示波器立马锁定故障范围】:https://www.bilibili.com/video/BV1pf421D73K?vd_source3cc3c07b09206097d0d8b0aefdf07958 可以用示波器查看MOS的输出波形来查看其是否损坏: 电源芯片的供电电压来回跳变…...
传值、传引用)
(程序设计语言)传值、传引用
1、传值(传递值): 在传值的情况下,函数接收到的是参数的一个副本,而不是参数本身。这意味着函数内部对参数的修改不会影响到原始值。传值通常用于基本数据类型(如整数、浮点数、布尔值等)的传递…...

一次基类类型对象无法被传递问题的分析
看下面一段代码: // proj2.cpp #include <iostream> using namespace std; class CharShape { public:CharShape(char ch) : _ch(ch) {};virtual void Show() 0; protected:char _ch; // 组成图形的字符 }; class Triangle : public CharShape { public:Tr…...
windows设置Redis服务后台自启动
问题 在日常开发过程中,redis是我们常用的缓存工具,但是由于redis对于Linux系统进行开发的,在Linux系统里可以通过修改redis.conf从而从而实现后台启动。 daemonize no 改成 daemonize yes 但是在window上如何也进行后台运行呢,…...
掌握Linux常用命令,扫平面试需求障碍
cd 切换目录。 > cd ../ #切换到父级目录 > cd /tmp # 切换到/tmp目录 > cd ~ # 切换到当前用户的家目录 ls命令 查看文件与目录的命令,list 的缩写。 > ls -l #列出长数据串,包含文件的属性与权限数据等 > ls -a #列出隐藏…...

c语言之文件打开模式
在c语言中,文件打开模式如下 r读模式: 允许对文件读取信息。若文件不存在,则会报错 w写模式: 允许向文件写入信息,若文件不存在,则创建一个文件 #include<stdio.h>int main() {FILE *fp;int i;char ay;fpfo…...
与禹老师学前端vue3学习汇总
24.5.15: 创建Vue3工程 1.确定自己电脑有没有nodejs环境,在cmd中输入node,如果出现Node.js的版本号说明已经有这个环境了,否则搜索Node.js安装 2.先在D盘创建一个文件夹Vue3_Study,然后在这个空文件夹中右键选择终端…...

Linux网络编程——HTTP协议的理解与运用
目录 前言 一、认识URL 二、认识HTTP样例 三、HTTP的报头内容 1.url 2. Content-Type 3.Method 方法 1.GET方法 2.POST方法 4、状态码 5.cookie和session 前言 我们知道,协议就是一种约定,客户端与服务端统一的用这种约定进行传输数据。我们…...

RestTemplate接口请求发送json、form数据格式以及处理接口错误状态码400 null
在使用RestTemplate发送HTTP请求时,你可以通过不同的方式发送JSON或表单数据(application/x-www-form-urlencoded)。同时,处理接口错误状态码(如400)和返回null的情况也是很重要的。以下是一些示例代码&…...

《Python编程从入门到实践》day29
# 昨日知识点回顾 修改折线图文字和线条粗细 矫正图形 使用内置格式 # 今日知识点学习 15.2.4 使用scatter()绘制散点图并设置样式 import matplotlib.pyplot as plt import matplotlib matplotlib.use(TkAgg)plt.style.use(seaborn-v0_8) # 使用内置格式 fig, ax plt.subpl…...

UIKit之图片浏览器
功能需求 实现一个图片浏览器,点击左右按钮可以切换背景图,且更新背景图对应的索引页和图片描述内容。 分析: 实现一个UIView的子类即可,该子类包含多个按钮。 实现步骤: 使用OC语言,故创建cocoa Touch类…...

如何查看SNMP设备的OID
什么是OID和MIB OID OID 代表对象标识符。 OID 唯一地标识 MIB 层次结构中的托管对象。 这可以被描述为一棵树,其级别由不同的组织分配。MIB MIB(管理信息基)提供数字化OID到可读文本的映射。 使用MIB Browser扫描OID 我的设备是一台UPS SN…...

什么?你设计接口什么都不考虑?
如果让你设计一个接口,你会考虑哪些问题? 1.接口参数校验 接口的入参和返回值都需要进行校验。 入参是否不能为空,入参的长度限制是多少,入参的格式限制,如邮箱格式限制 返回值是否为空,如果为空的时候是…...

2024年3月 青少年等级考试机器人理论真题二级
202403 青少年等级考试机器人理论真题二级 第 1 题 一个机器小车,用左右两个电机分别控制左右车轮,左侧电机转速是100rpm,右侧电机转速是50rpm,则此机器小车?( ) A:原地右转 B&am…...
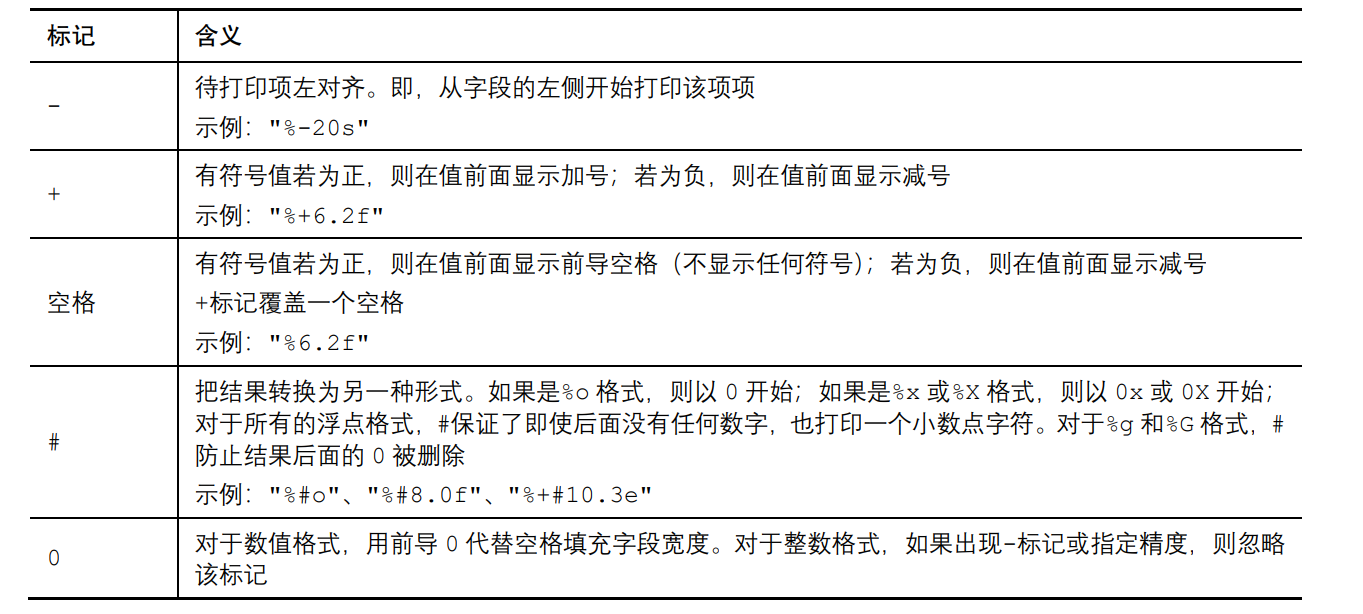
C语言学习【printf函数和scanf函数】
C语言学习【printf函数和scanf函数】 printf()函数和scanf()函数可以让用户与程序交流,是输入/输出函数 printf()函数 请求printf()函数打印数据的指令要与待打印数据的类型相匹配。例如,打印整数时使用%d,打印字符时使用%c。这些符号被称…...

shell正则表达式
sort命令 以行为单位对文件内容进行排序,也可以根据不同的数据类型来排序 比较原则是从首字符向后,依次按ASCII码值进行比较,最后将他们按升序输出。 sort 对行内容进行升序排序 XXX | sort 选项 sort 选项 文件 常用选项&#x…...

react组件渲染性能优化之函数组件-useCallback使用
useCallback主要就是对函数进行缓存,useCallBack这个Hooks主要是解决React.memo不能缓存事件的问题 useCallBack(fn, dependencies) :fn想要缓存的函数,dependencies有关是否更新 fn 的所有响应式值的一个列表 比如:UseCallBackOptimize组件…...
【C++】:string类的基本使用
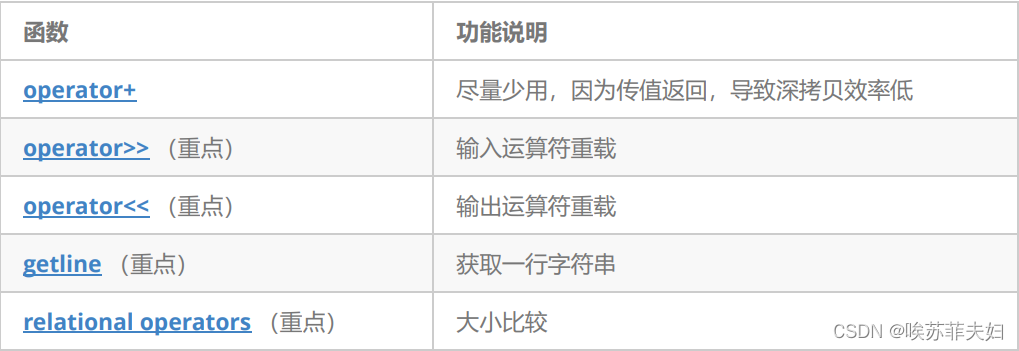
目录 引言一,string类对象的常见构造二,string类对象的容量操作三,string类对象的访问及遍历操作四,string类对象的修改操作五,string类非成员函数六,整形与字符串的转换 引言 string 就是我们常说的"…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
