C++二叉搜索树搜索二叉树二叉排序树
C++二叉搜索树
1. 二叉搜索树的概念
二叉搜索树(BST,Binary Search Tree),也称为二叉排序树或二叉查找树。它与一般二叉树的区别在于:每个结点必须满足“左孩子大于自己,右孩子小于自己”的规则。在这种规则的约束下,二叉搜索树使用中序遍历出来的数据是一个由小到大排列的结果。
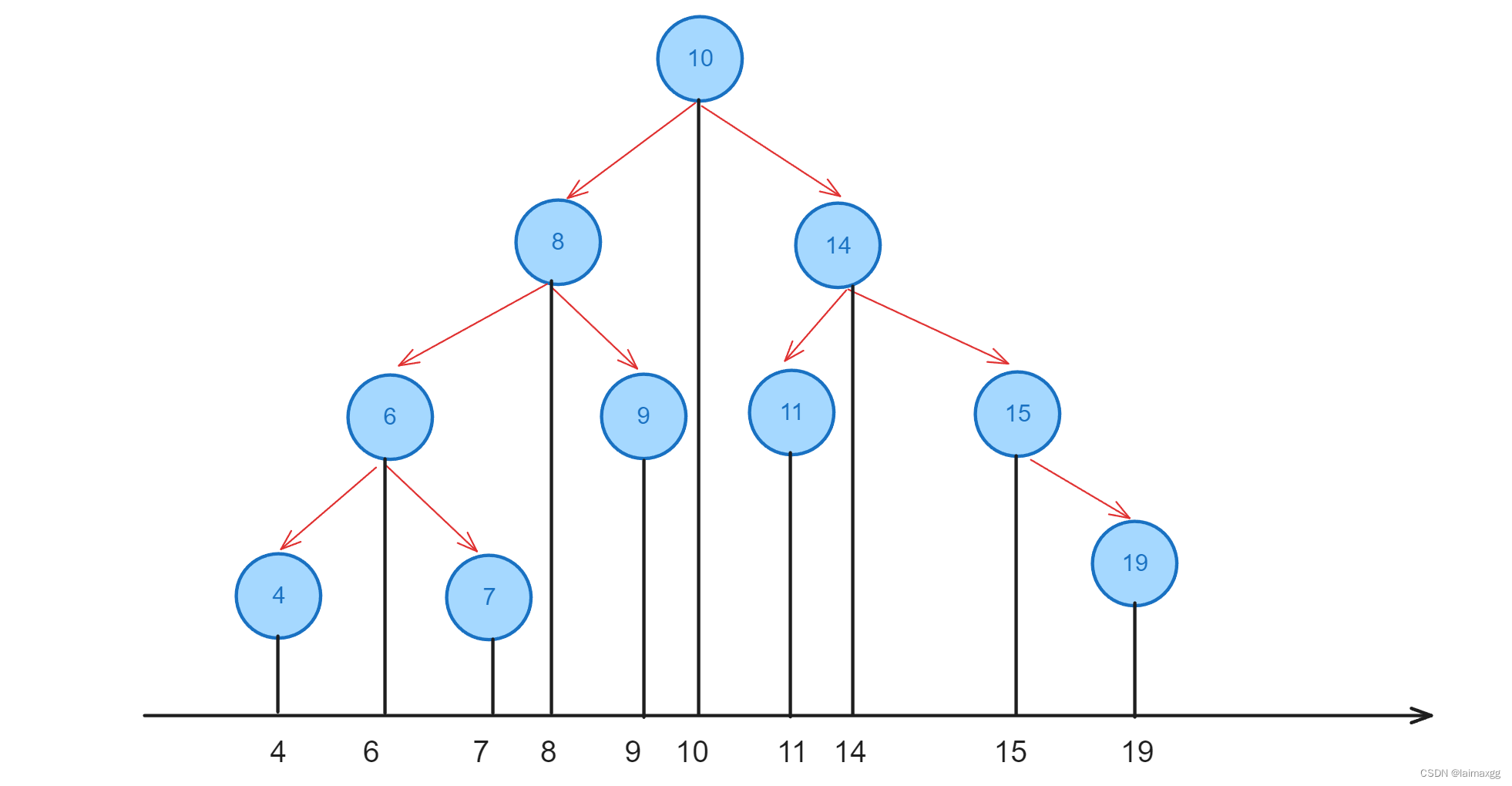
优点:
- 查找某个值最多只需要遍历高度次即可,效率高。
- 使用中序遍历出来的数据是有序的。
缺点:
- 结点的值不允许修改,否则破坏树的结构。
2. 二叉搜索树的插入
二叉搜索树的插入很简单,首先用插入的值从根结点开始比较。插入值小于结点值向左,插入值大于结点值向右,直到结点的左孩子或右孩子为空时结束,为空的位置就是插入的位置。
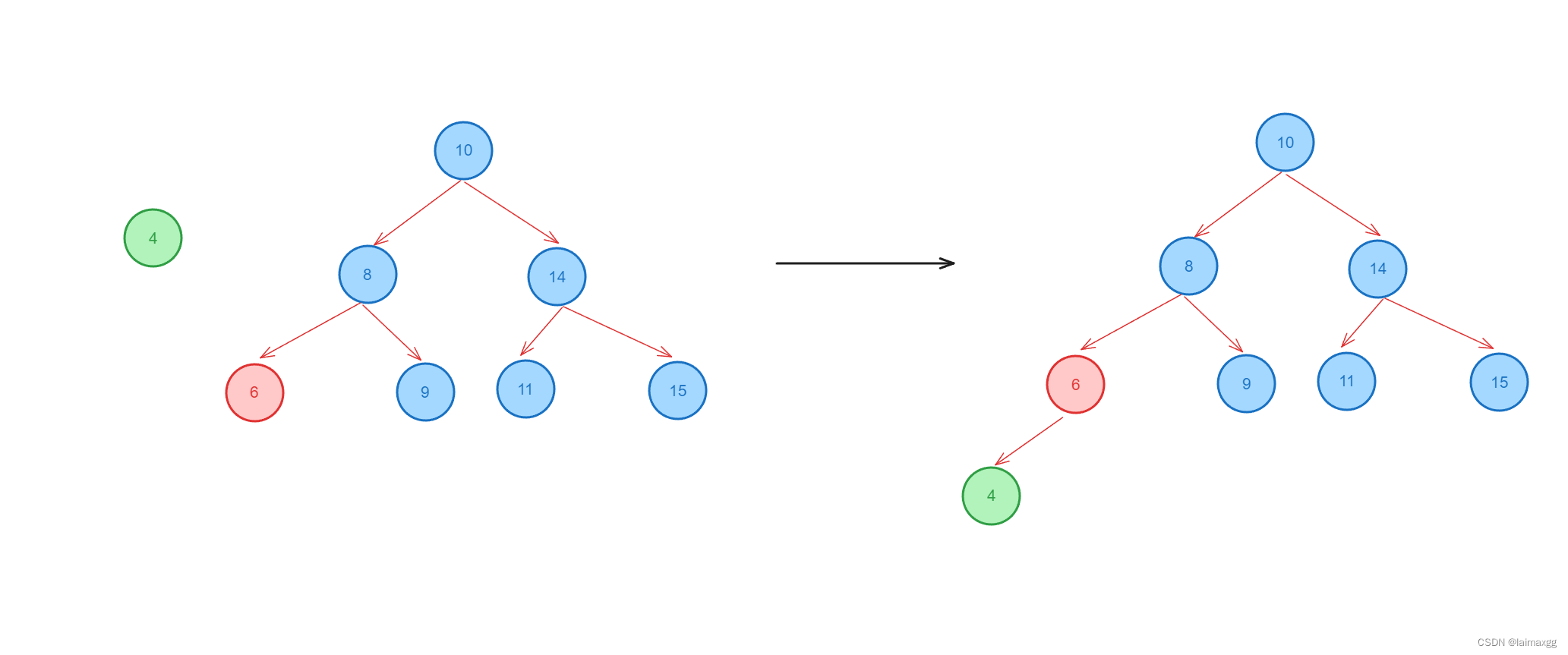
4作为插入结点的值,先找到6是插入结点的父结点,再判断4和6的大小关系,4<6,所以插入在6的左边。
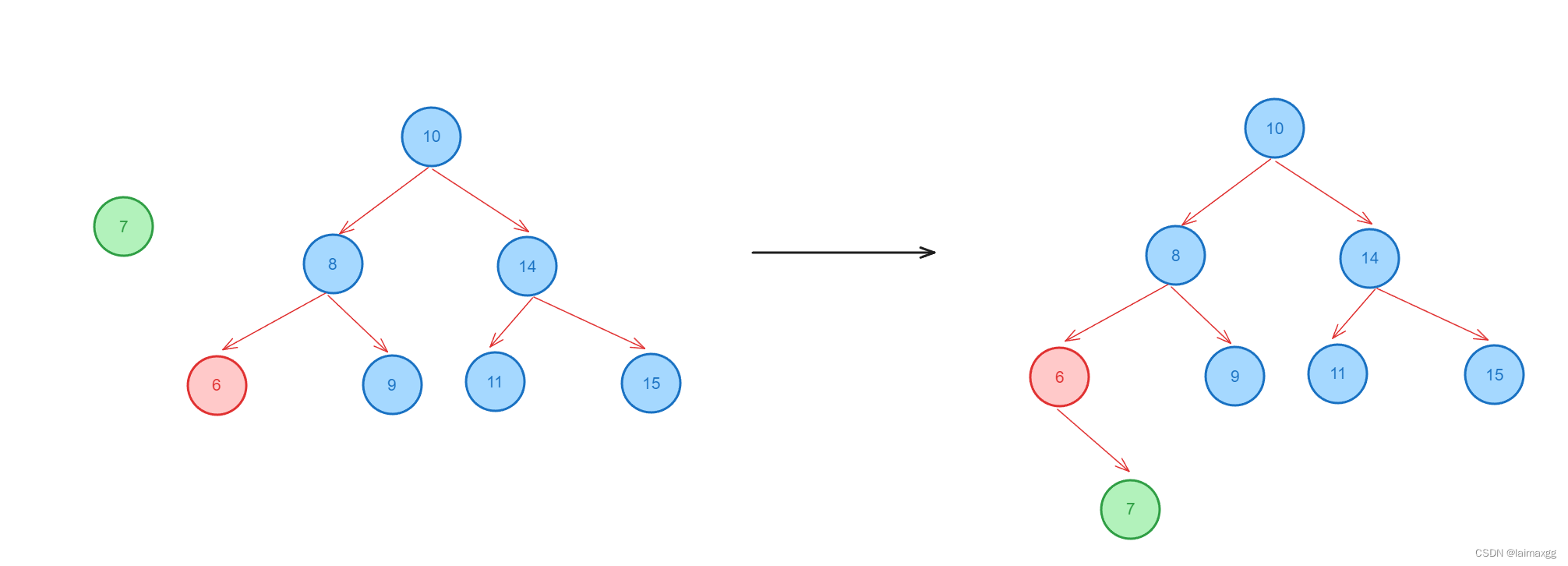
7作为插入结点的值,先找到6是插入结点的父结点,再判断7和6的大小关系,7>6,所以插入在6的右边。
3. 二叉搜索树的删除
二叉搜索的删除需要分两种情况:
3.1 删除的结点是叶子结点
如果删除的结点是叶子结点,将该结点的父结点指针制空,再释放该结点即可。
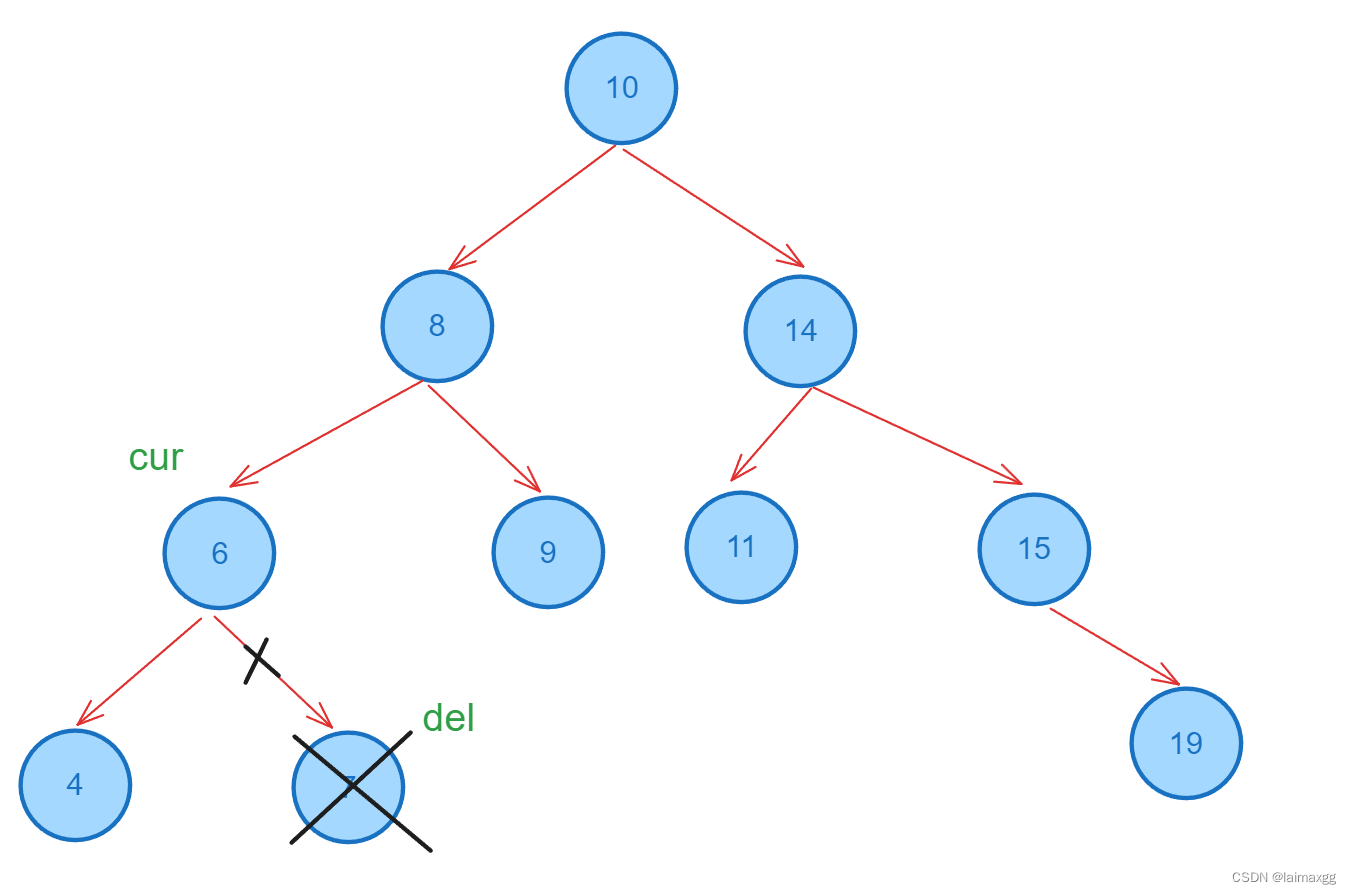
3.2 删除的结点不是叶子结点
如果删除的结点不是叶子结点,可以分为三种情况讨论:
3.2.1 左子树为空
如果删除的结点的左子树为空,此时需要判断删除结点与其父子树的关系:我是父结点的左孩子,就让父结点的左指向我的右子树;我是父结点的右孩子,就让父结点的右指向我的右子树
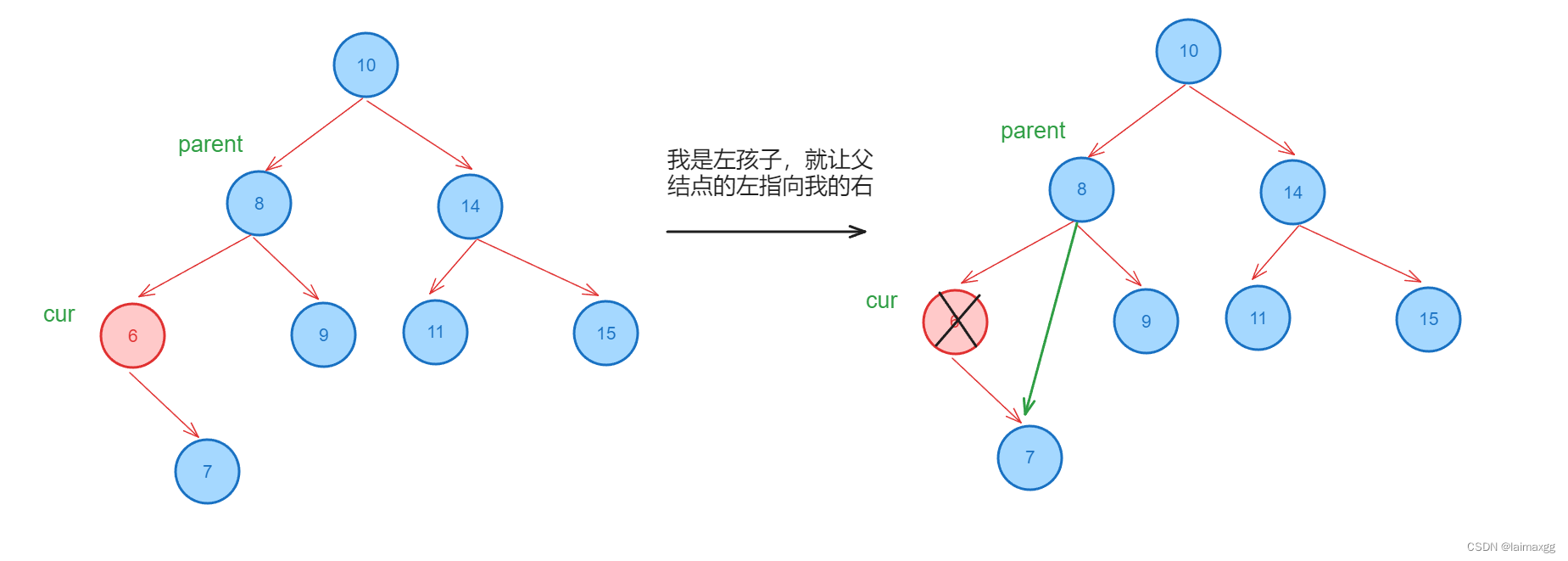
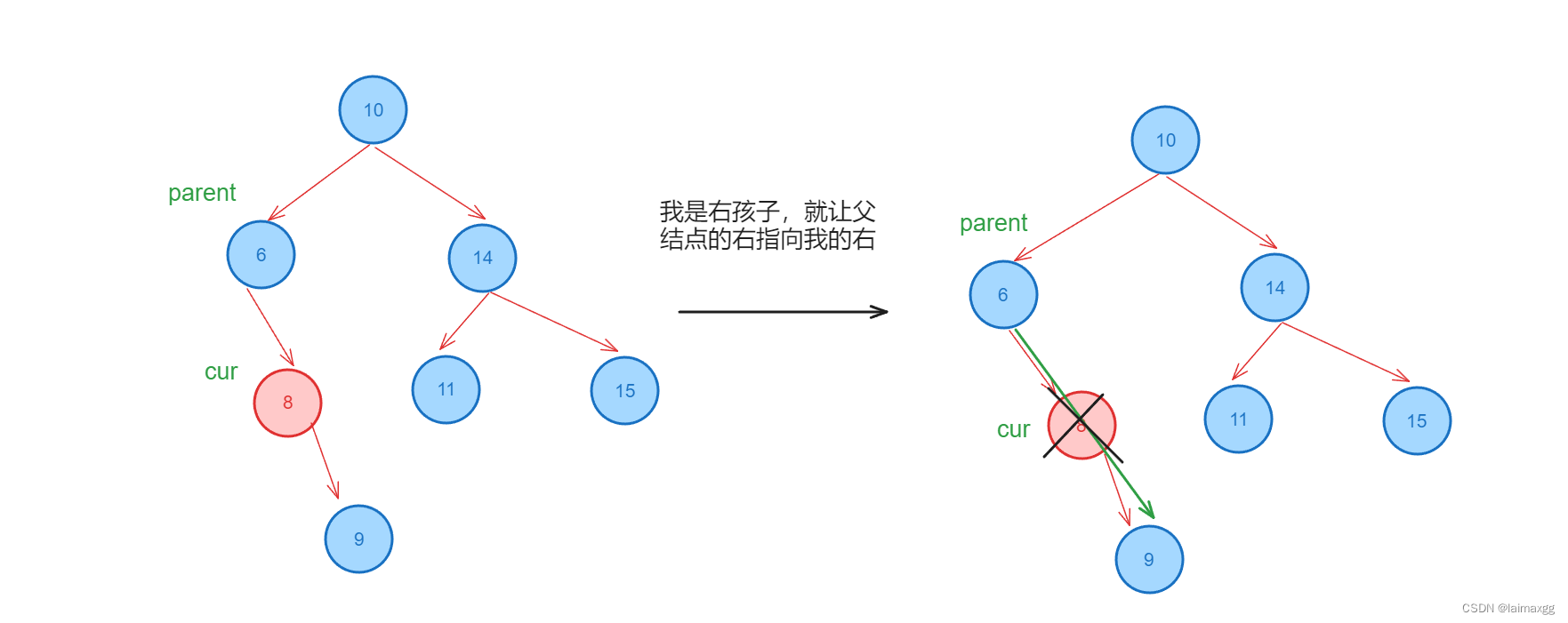
3.2.2 右子树为空
右子树为空,原理与上相同,只是父结点改变的是左的指向。
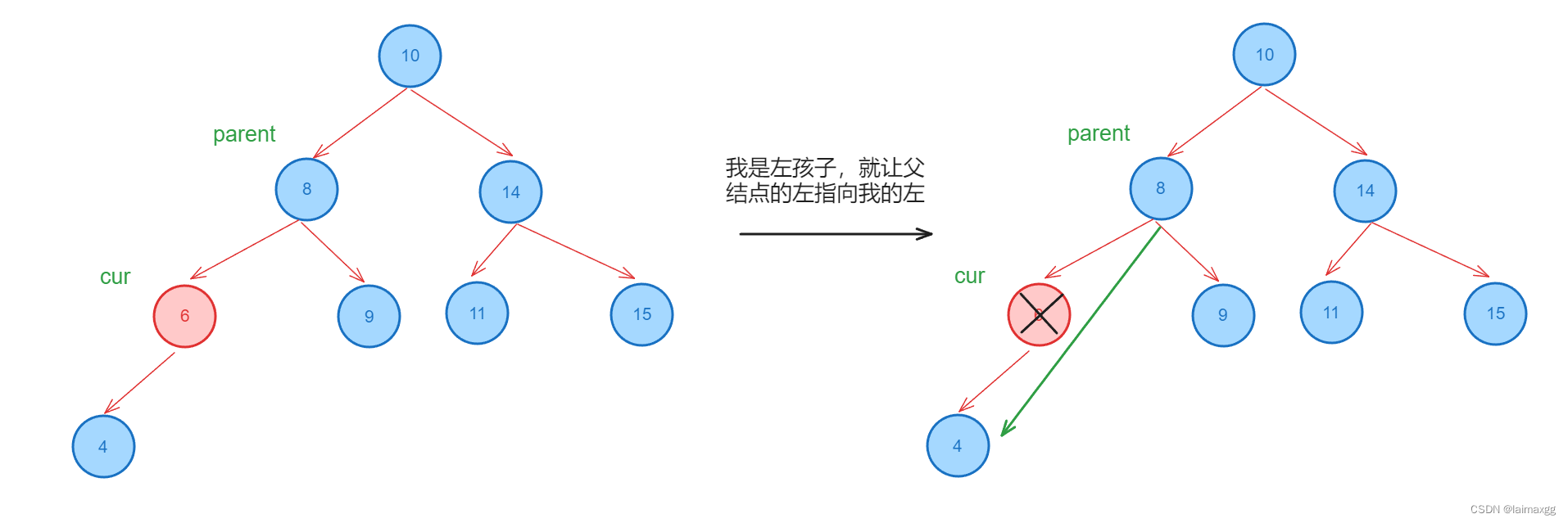

3.2.3 左右子树不为空
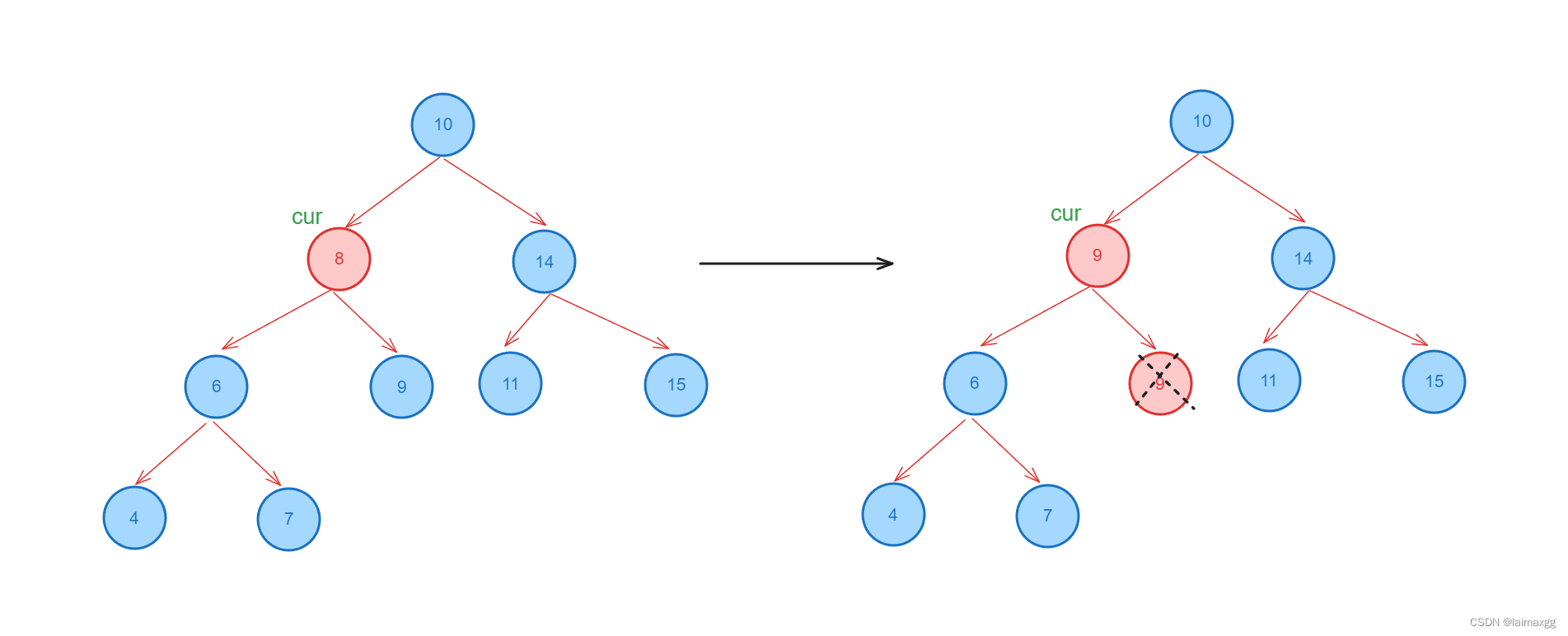
如果删除结点的左右子树都不为空,那么此时就需要使用替换法的思想。替换法可以使用左子树的最大结点或右子树的最小结点作为替换结点来替换当前结点,再将替换结点删除。所谓“替换”在实际操作中不是把两个结点的值互换,而是将替换结点的值赋给原删除结点,因为替换节点最终要删除,所以不必要对其进行真正的替换操作。
使用最左结点替换:
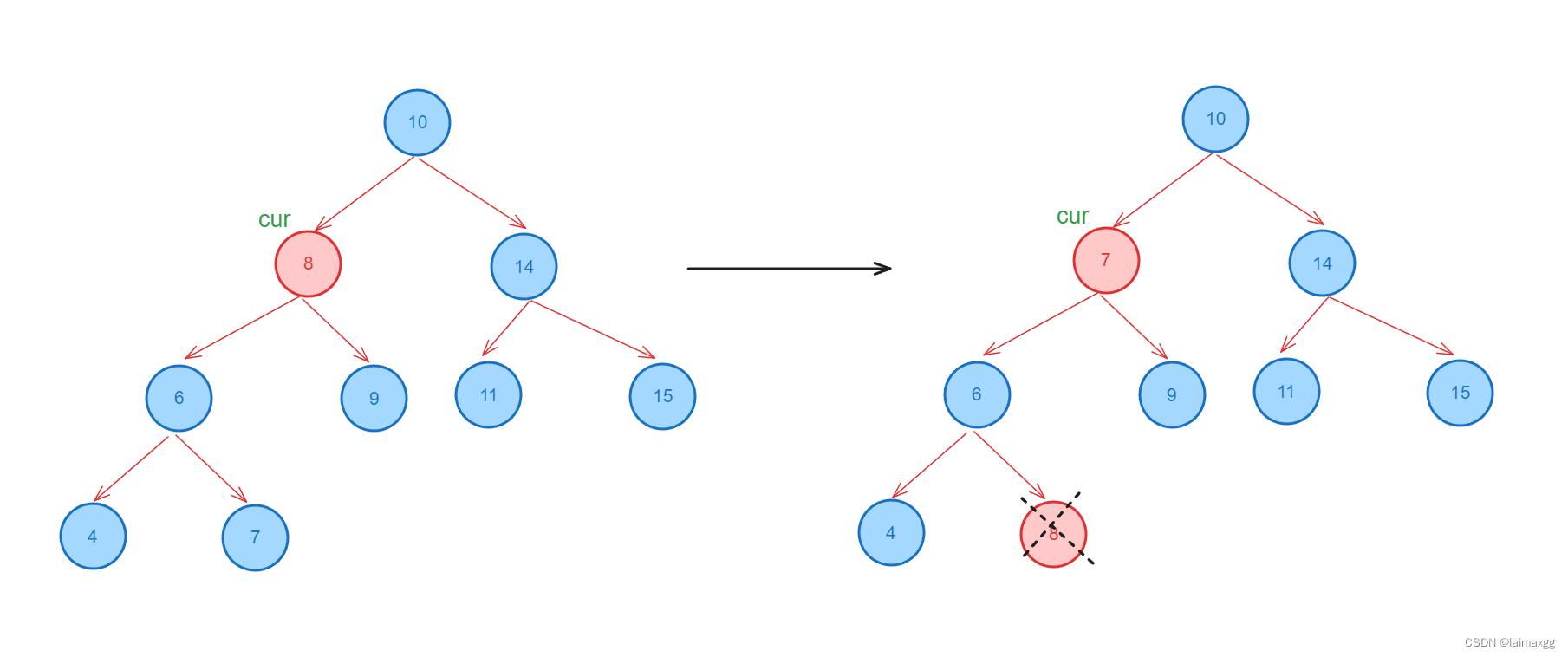
使用最右结点替换:
4.二叉搜索树的退化问题
二叉搜索树的最优情况下,查找效率为logN。但当插入的顺序有序或部分有序时,二叉搜索树的查找效率会下降,极端情况下会退化至N
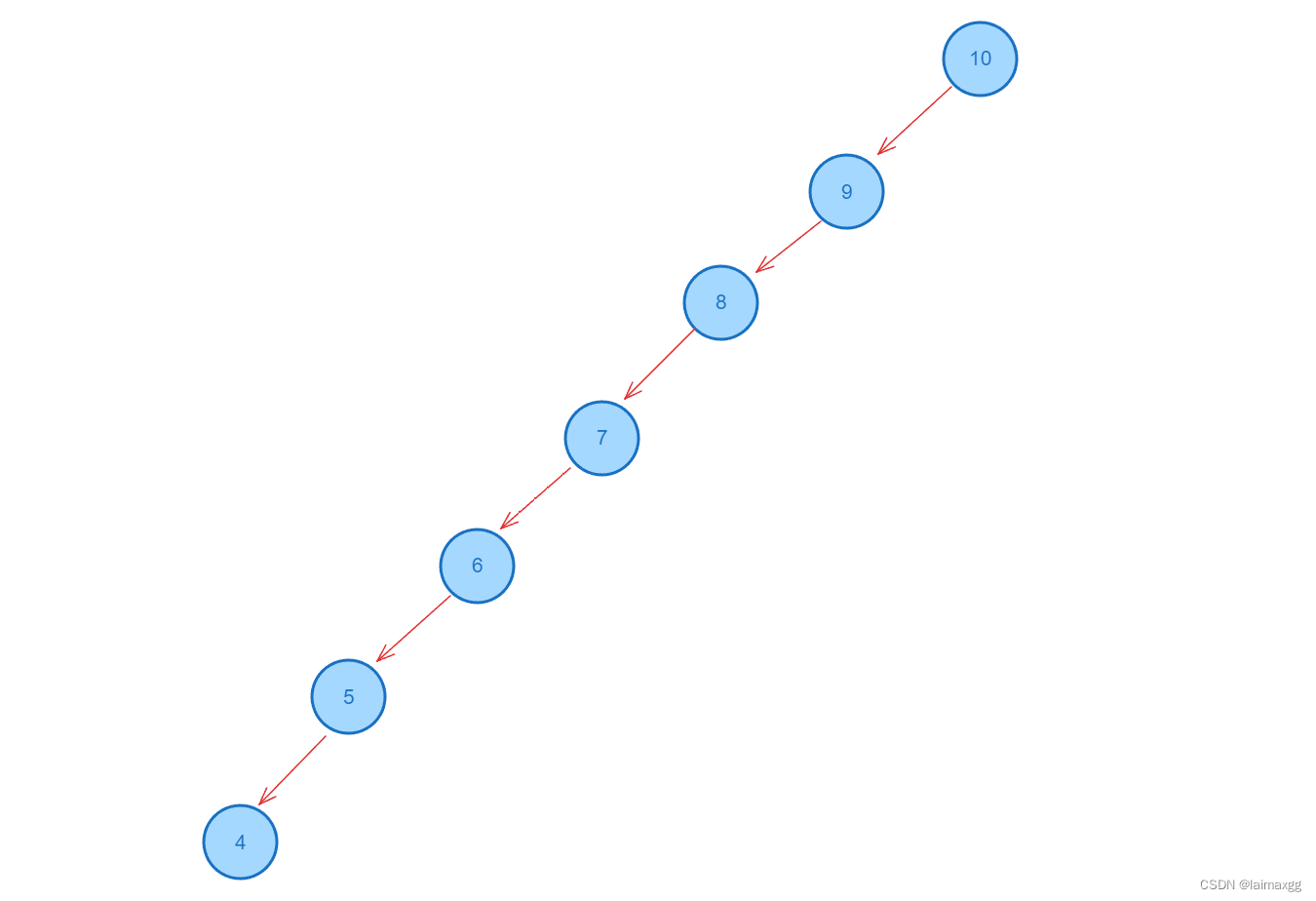
按{10,9,8,7,6,5,4}的顺序插入,导致二叉搜索树完全退化。
5. 参考代码
template<class K, class V>
struct BSTreeNode
{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key,const V& value):_left(nullptr),_right(nullptr),_key(key),_value(value){}
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);{if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return cur;}}return nullptr;}bool Erase(const K& key){//先找到该结点Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//如果删除的是叶子结点,直接删除if (cur->_left == nullptr && cur->_right == nullptr){if (cur == parent->_left)parent->_left = nullptr;else if (cur == parent->_right)parent->_right = nullptr;delete cur;}//如果左为空else if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else if (cur == parent->_right){parent->_right = cur->_right;}}delete cur;}//如果右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else if (cur == parent->_right){parent->_right = cur->_left;}}delete cur;}// 如果左右都不为空else{//查找右子树的最左结点替换Node* RightMinParent = cur;Node* RightMin = cur->_right;while (RightMin->_left){RightMinParent = RightMin;RightMin = RightMin->_left;}cur->_key = RightMin->_key;cur->_value = RightMin->_key;cur->_value = RightMin->_value;if (RightMinParent->_left == RightMin){RightMinParent->_left = nullptr;}else{RightMinParent->_right = nullptr;}delete RightMin;}return true;}}return false;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}
private:Node* _root = nullptr;
};相关文章:

C++二叉搜索树搜索二叉树二叉排序树
C二叉搜索树 1. 二叉搜索树的概念 二叉搜索树(BST,Binary Search Tree),也称为二叉排序树或二叉查找树。它与一般二叉树的区别在于:每个结点必须满足“左孩子大于自己,右孩子小于自己”的规则。在这种规则的约束下,二…...

Java 自然排序和比较器排序区别?Comparable接口和Comparator比较器区别?
注:如果你对排序不理解,请您耐心看完,你一定会明白的。文章通俗易懂。建议用idea运行一下案例。 1)自然排序和比较器排序的区别? 自然排序是对象本身定义的排序规则,由对象实现 Comparable 接口ÿ…...

【CV】opencv调用DIS/LK等计算光流,前一帧和当前帧写反了有什么影响?
当在计算光流时,将前一帧和当前帧输入反了,会导致一系列问题。 在计算光流时,通常是将前一帧作为模板,根据当前帧计算光流。因为光流是描述相邻帧之间像素移动的一种方法,它通过比较两帧之间的像素强度或特征点的移动…...

C语言学习细节|C语言面向对象编程!函数指针如何正确使用
文章目录 1.函数指针定义2.格式3.应用回调函数动态函数调用函数的间接调用 4.结构体与函数指针结合 1.函数指针定义 函数指针就是一个指向函数的指针变量,与指向数据的指针不同,函数指针保存的是函数的地址,这使得程序可以动态地调用不同的函…...

C语言简要(一)
总得让她开心吧 helloworld #include <stdio.h>int main() {printf("hello world!\n");return 0; } 程序框架 #include <stdio.h> int main {return 0; }输出 printf("hello world!\n"); "里面的内容叫做“字符串”,prin…...

那些年我与c++的叫板(一)--string类自实现
引子:我们学习了c中的string类,那我们能不能像以前数据结构一样自己实现string类呢?以下是cplusplus下的string类,我们参考参考! 废话不多说,直接代码实现:(注意函数之间的复用&…...
)
二刷算法训练营Day08 | 字符串(1/2)
今日任务: 344.反转字符串 541. 反转字符串II卡码网:54.替换数字 151.翻转字符串里的单词卡码网:55.右旋转字符串 详细布置: 1. 344. 反转字符串 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 …...

使用高防IP是应对网络安全的重要措施
使用高防IP(High Defense IP)在现代网络环境中显得尤为重要,这主要源于以下几个方面的原因: 一、网络安全形势严峻 随着互联网的快速发展,网络安全问题日益突出。各种网络攻击手段层出不穷,如分布式拒绝服…...

代码随想录-算法训练营day40【动态规划03:整数拆分、不同的二叉搜索树】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第九章 动态规划part03● 343.整数拆分 ● 096.不同的二叉搜索树 详细布置 今天两题都挺有难度,建议大家思考一下没思路,直接看题解,第一次做,硬想很难想出来。343. 整数…...
MySQL数据库中基本数据管理操作
使用SQL语句实现基本数据管理操作——即DML语句 1.添加数据 insert into 表名(字段名称,字段名称,字段名称)values(数据,数据,数据) 在MySQL数据库中,除了数字&#x…...

记录一下Hql遇到的零碎问题
建表相关 -- 地区维度表 drop table dim_province_full; create table dim_province_full( id string comment 编号, name string comment 省份名称, region_id string comment 大区id, area_code string comment 行政区位码, iso_code string comment 国际编码, iso_3166_2 s…...

Flutter 中的 TextField 小部件:全面指南
Flutter 中的 TextField 小部件:全面指南 在 Flutter 中,TextField 是一个允许用户输入文本的小部件。它非常灵活,支持多种文本输入场景,如单行文本、多行文本、密码输入、数值输入等。TextField 还提供了丰富的定制选项…...
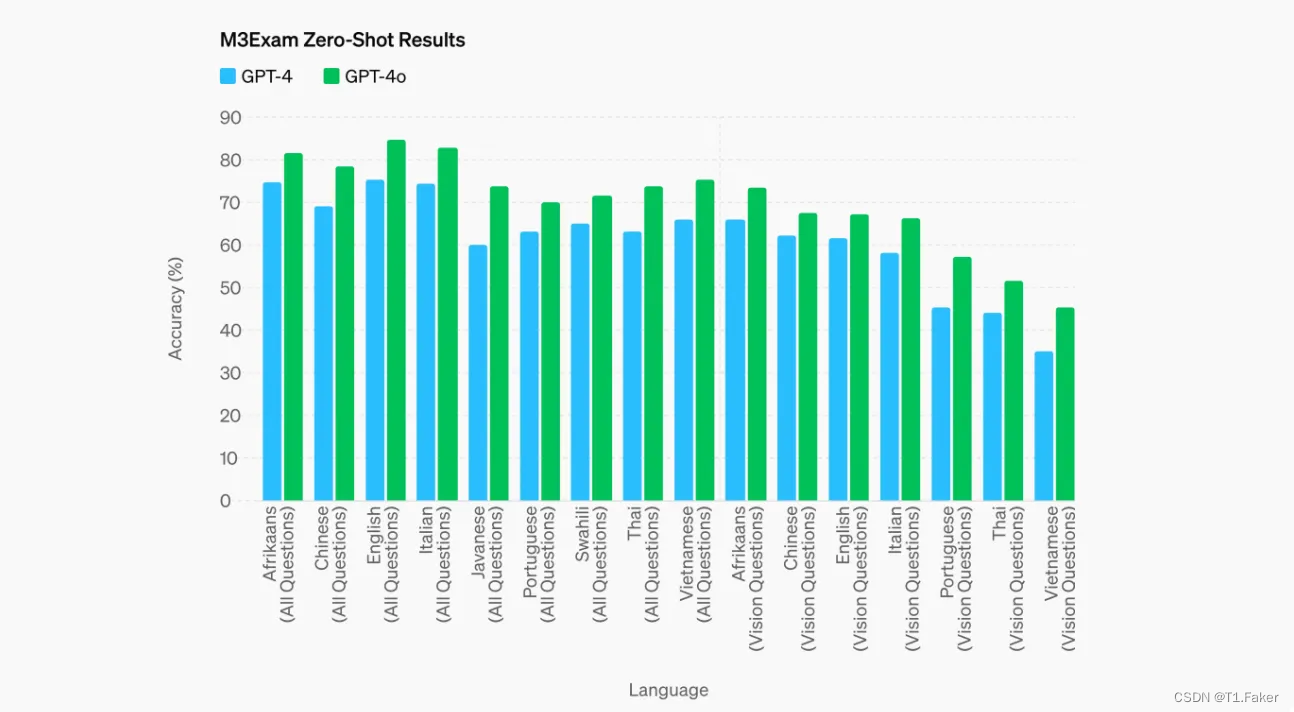
GPT-4o:全面深入了解 OpenAI 的 GPT-4o
GPT-4o:全面深入了解 OpenAI 的 GPT-4o 关于 GPT-4o 的所有信息ChatGPT 增强的用户体验改进的多语言和音频功能GPT-4o 优于 Whisper-v3M3Exam 基准测试中的表现 GPT-4o 的起源追踪语言模型的演变GPT 谱系:人工智能语言的开拓者多模式飞跃:超越…...

2024中国应急(消防)品牌巡展西安站成功召开!惊喜不断
消防品牌巡展西安站 5月10日,由中国安全产业协会指导,中国安全产业协会应急创新分会、应急救援产业网联合主办,陕西消防协会协办的“一切为了安全”2024年中国应急(消防)品牌巡展-西安站成功举办。该巡展旨在展示中国应急(消防&am…...

信创电脑|暴雨新增兆芯KX-7000处理器版本
IT世界 5 月 15 日消息,暴雨公司信创家族新上架了一款搭载兆芯KX-7000系列处理器、摩尔线程8GB 显卡、16G DDR5 内存以及 512G SSD 的新配置台式电脑主机。 兆芯 KX-7000 处理器采用开先的 8 核 Chiplet互联架构,最高频率3.7 GHz,拥有 32MB 的…...

面向对象 07:抽象类相关知识,抽象类的基本概念,使用方式,以及一些注意事项
一、前言 记录时间 [2024-05-15] 系列文章简摘: 面向对象 03:类与对象的创建、初始化和使用,通过 new 关键字调用构造方法,以及创建对象过程的内存分析 面向对象 04:三大特性之——封装,封装的含义和作用&a…...

Rust中的链式调用方法
在Rust编程语言中,链式调用是一种流行的编程模式,它允许开发者以流畅、连续的方式调用多个方法。这种风格不仅提高了代码的可读性,而且使得复杂的操作可以串联在一起,形成一个清晰、简洁的语句。在Rust中,链式调用主要…...

xCode升级后: Library ‘iconv2.4.0’ not found
报错信息: targets 选中 xxxNotification: Build Phases ——> Link Binary With Libraries 中,移除 libiconv.2.4.0.tbd libiconv.2.4.0.dylib 这两个库(只有一个的移除一个就好)。 然后重新添加 libiconv.tbd 修改完…...

SQL语言:完整性约束
完整性约束 数据完整性是指存储在数据库中的数据要能正确反映实际情况,规定输入的数据不能是无效值、错误值 或者乱码等。 一、非空约束: 非空约束关键字: not null 1、非空约束的创建 create table teacher( t_id int not null, -- 为教…...

UBUNTU下CMAKE指定执行文件运行时查找库的路径
在Ubuntu下,使用CMake时,如果需要指定执行文件运行时库的搜索路径,可以在CMakeLists.txt文件中通过set_target_properties命令来设置。 以下是一个示例,假设你的目标是一个名为my_application的可执行文件,你想要添加…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
