【回溯算法】【Python实现】TSP旅行售货员问题
文章目录
- @[toc]
- 问题描述
- 回溯算法
- `Python`实现
- 时间复杂性
文章目录
- @[toc]
- 问题描述
- 回溯算法
- `Python`实现
- 时间复杂性
问题描述
- 给定一组城市和它们之间的距离矩阵,找到一条距离最短的路径,使得旅行商从一个城市出发,经过所有城市恰好一次,并最终回到出发城市
回溯算法
-
旅行售货员问题的解空间是一棵排列树
-
当 i = n i = n i=n时,算法搜索至叶结点,其相应的路径长度为 c d cd cd,如果 c d < b e s t d cd < bestd cd<bestd,则表示当前解优于当前最优解,此时更新 b e s t d bestd bestd
-
当 i < n i < n i<n时,当前扩展结点位于排列树的第 i i i层,图 G G G中存在从顶点 x [ i ] x[i] x[i]到顶点 x [ i + 1 ] x[i + 1] x[i+1]的边时, x [ 1 : i + 1 ] x[1 : i + 1] x[1:i+1]构成图 G G G的一条路径,且当 x [ 1 : i + 1 ] x[1 : i + 1] x[1:i+1]的路径长度小于当前最优值时算法进入排列树的第 i + 1 i + 1 i+1层,否则将剪去相应的子树
Python实现
import numpy as npdef backtrack_tsp(cities):n = len(cities)visited = [False] * n # 记录城市是否已经被访问shortest_path = []shortest_distance = float('inf')def distance(city1, city2):x1, y1 = city1x2, y2 = city2return np.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2)# 创建距离矩阵dist_matrix = np.zeros((n, n))for i in range(n):for j in range(n):dist_matrix[i][j] = distance(cities[i], cities[j])def backtrack(path, distance):nonlocal shortest_path, shortest_distanceif len(path) == n: # 所有城市都已经访问过distance += dist_matrix[path[-1]][path[0]] # 回到起点的距离if distance < shortest_distance: # 更新最短路径和最短距离shortest_path = path[:]shortest_distance = distancereturnlast_city = path[-1] if path else 0 # 上一个访问的城市for next_city in range(n):if not visited[next_city]:visited[next_city] = Truepath.append(next_city)distance += dist_matrix[last_city][next_city]backtrack(path, distance)# 恢复回溯前状态distance -= dist_matrix[last_city][next_city]path.pop()visited[next_city] = False# 开始回溯搜索visited[0] = Truebacktrack([0], 0)return shortest_path, shortest_distancecities = [(0, 0), (1, 5), (2, 3), (5, 2), (6, 4)]
shortest_path, shortest_distance = backtrack_tsp(cities)print(f'最短路径: {shortest_path}')
print(f'最短距离: {shortest_distance}')
最短路径: [0, 2, 1, 4, 3]
最短距离: 18.56187155119086
时间复杂性
- 回溯算法解
TSP问题的时间复杂性为 O ( n ! ) O(n!) O(n!)
相关文章:

【回溯算法】【Python实现】TSP旅行售货员问题
文章目录 [toc]问题描述回溯算法Python实现时间复杂性 问题描述 给定一组城市和它们之间的距离矩阵,找到一条距离最短的路径,使得旅行商从一个城市出发,经过所有城市恰好一次,并最终回到出发城市 回溯算法 旅行售货员问题的解空间…...

Java处理xml
Java处理xml DOM(Document Object Model)读取写入参考文献[Java DOM 教程](https://geek-docs.com/java/java-tutorial/dom.html#ftoc-heading-5) DOM(Document Object Model) Java的DOM(Document Object Model&#…...

软考中级-软件设计师 (十一)标准化和软件知识产权基础知识
一、标准化基础知识 1.1标准的分类 根据适用的范围分类: 国际标准指国际化标准组织(ISO)、国际电工委员会(IEC)所制定的标准,以及ISO所收录的其他国际组织制定的标准。 国家标准:中华人民共和…...

pytest教程-46-钩子函数-pytest_sessionstart
领取资料,咨询答疑,请➕wei: June__Go 上一小节我们学习了pytest_report_testitemFinished钩子函数的使用方法,本小节我们讲解一下pytest_sessionstart钩子函数的使用方法。 pytest_sessionstart 是 Pytest 提供的一个钩子函数,…...
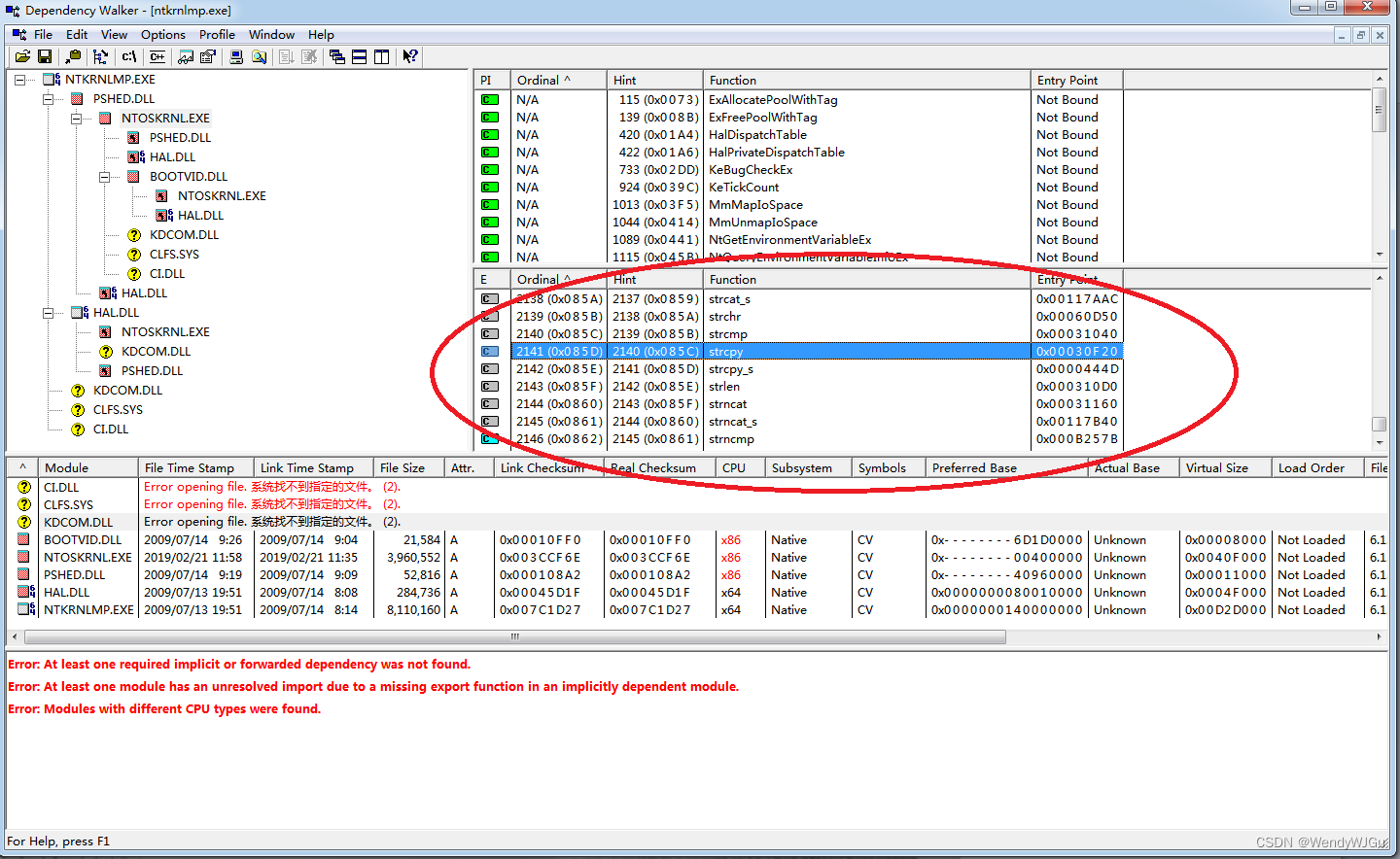
Windows内核函数 - ASCII字符串和宽字符串
本章介绍了Windows内核中字符串处理函数、文件读写函数、注册表读写函数。这些函数是DDK提供的运行时函数,他们比标准C语言的运行时函数功能更丰富。普通的C语言运行时库是不能在内核模式下使用的,必须使用DDK提供的运行时函数。 和应用程序一样…...

从零开始学习MySQL 事务处理
事务处理与ACID特性 事务是数据库操作的基本单元,它确保一组操作要么全部成功,要么全部失败,以此来维护数据库的一致性。这四个字母缩写ACID代表了事务的四大特性: 原子性(Atomicity)**:事务被…...

字符数组以及字符串相关的几个函数
一.字符数组 1.定义:格式如下 char a[10]; //此处就表示定义了一个长度为10的字符数组 2.引用: 也和其余的数组一样,是下标引用。 3.初始化: 如下代码为字符数组初始化的几种情况: int main() {char arr[5] {…...

AOP面向切面编程
1,注入依赖 <!--web--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</grou…...
C# WinForm —— 15 DateTimePicker 介绍
1. 简介 2. 常用属性 属性解释(Name)控件ID,在代码里引用的时候会用到,一般以 dtp 开头Format设置显示时间的格式,包含Long: Short: Time: Custom:采用标准的时间格式 还是 自定义的格式CustomFormat自定…...

SpringBoot中六种批量更新Mysql 方式效率对比
SpringBoot中六种批量更新Mysql 方式效率对比 先上结论吧,有空可以自测一下,数据量大时运行一次还时挺耗时的 效率比较 小数据量时6中批量更新效率不太明显,根据项目选择合适的即可,以1万条为准做个效率比较,效率从高到低一次排名如下 replace into和ON DUPLICATE KEY效率最…...
【SpringBoot】SpringBoot整合jasypt进行重要数据加密
📝个人主页:哈__ 期待您的关注 目录 📕jasypt简介 🔥SpringBoot使用jasypt 📂创建我需要的数据库文件 📕引入依赖 🔓配置数据库文件(先不进行加密) 🌙创…...

【Go语言入门学习笔记】Part1.梦开始的地方
一、前言 经过一系列的学习,终于有时间来学习一些新的语言,Go语言在现在还是比较时髦的,多一个技能总比不多的好,故有时间来学一下。 二、配置环境 按照网络中已有的配置方法配置好,本人采用了Jetbrain的Goland&#…...
附Python代码)
数据特征降维 | 主成分分析(PCA)附Python代码
主成分分析(Principal Component Analysis,PCA)是一种常用的数据降维技术和探索性数据分析方法,用于从高维数据中提取出最重要的特征并进行可视化。 PCA的基本思想是通过线性变换将原始数据投影到新的坐标系上,使得投影后的数据具有最大的方差。这些新的坐标轴称为主成分…...

当服务实例出现故障时,Nacos如何处理?
当服务实例出现故障时,Nacos的应对策略 在微服务架构日益盛行的今天,服务之间的稳定性与可靠性成为了我们架构师们不得不面对的重要课题。尤其是在面对服务实例出现故障时,如何确保整个系统的稳定运行,成为了我们首要考虑的问题。…...
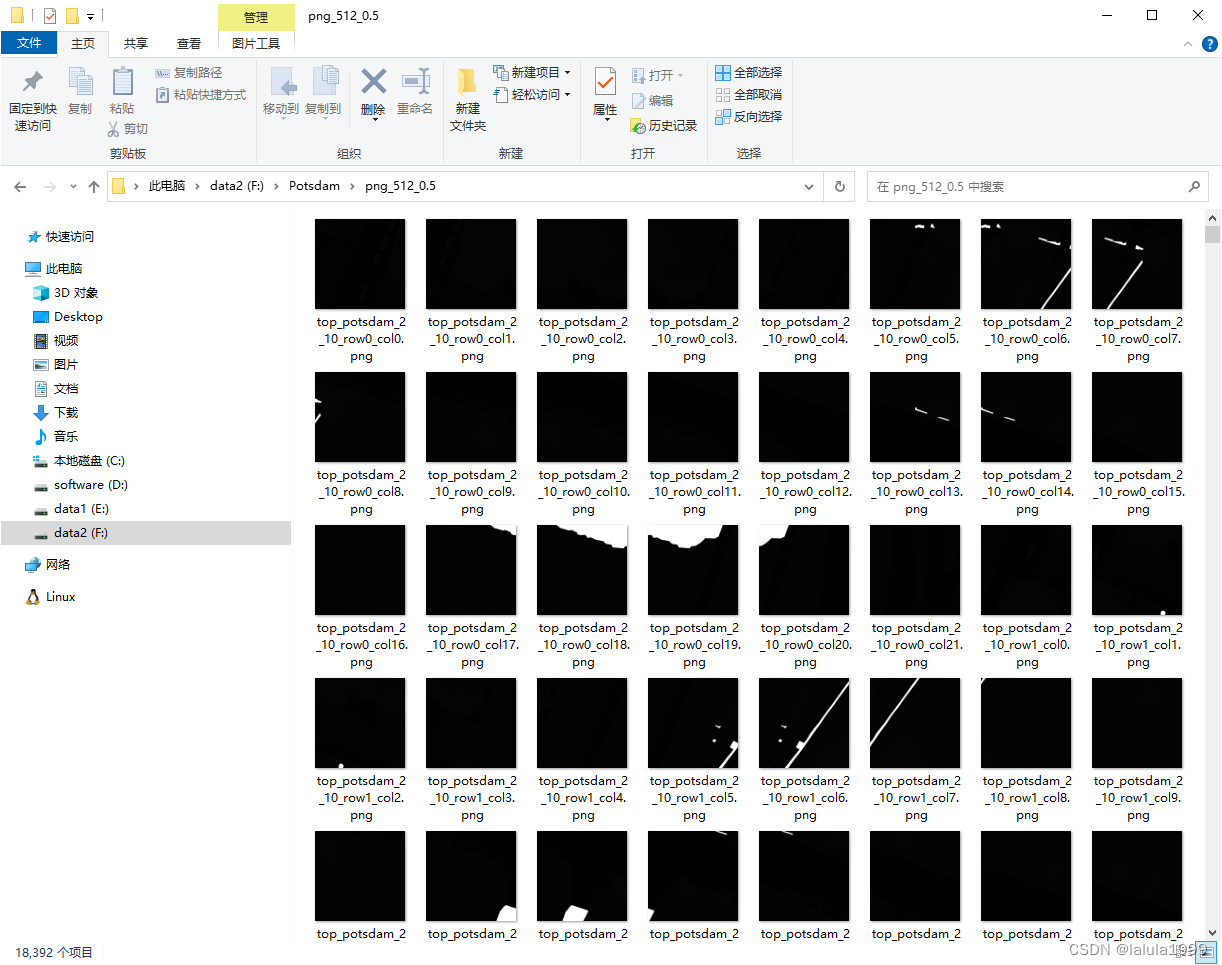
遥感数据集制作(Potsdam数据集为例):TIF图像转JPG,TIF标签转PNG,图像重叠裁剪
文章目录 TIF图像转JPGTIF标签转PNG图像重叠裁剪图像重命名数据集转COCO格式数据集转VOC格式 遥感图像不同于一般的自然图像,由于波段数量、图像位深度等原因,TIF图像数据不能使用简单的格式转换方法。本文以Potsdam数据集为例,制作能够直接用…...

根据web访问日志,封禁请求量异常的IP,如IP在半小 时后恢复正常则解除封禁
在网络安全日益受到重视的今天,如何有效防范恶意流量和攻击成为了每个网站管理员必须面对的问题。恶意流量不仅会影响网站的正常运行,还可能导致服务器崩溃,给网站带来不可估量的损失。为了应对这一问题,我们特别推出了一款实用的…...
)
2.go语言初始(二)
本篇博客涉及到go 的基础数据类型、 go 语言中的运算符、转义字符、格式化输出、字符串操作 go 语言中的运算符 在 go 语言中,基本数据类型主要包括以下几类:整数类型、浮点数类型、复数类型、布尔类型、字符串类型、字节类型(byte…...

MQTT对比HTTP
吞吐量:根据3G网络的测量结果,MQTT的吞吐量比HTTP快93倍。这意味着在相同的网络条件下,MQTT能够更有效地传输数据,从而在处理大量数据或实时数据传输时具有更高的效率。架构与模式:MQTT基于发布/订阅模型,提…...
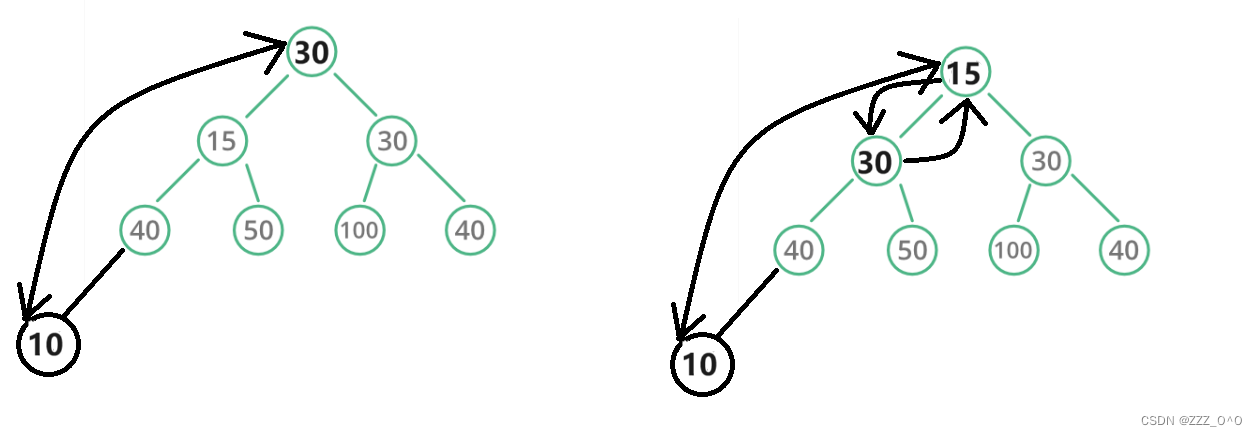
暴力数据结构之二叉树(堆的相关知识)
1. 堆的基本了解 堆(heap)是计算机科学中一种特殊的数据结构,通常被视为一个完全二叉树,并且可以用数组来存储。堆的主要应用是在一组变化频繁(增删查改的频率较高)的数据集中查找最值。堆分为大根堆和小根…...

死锁调试技巧:工作线程和用户界面线程
有人碰到了一个死锁问题,找到我们想请我们看看,这个是关于应用程序用户界面相关的死锁问题。 我也不清楚他为什么会找上我们,可能是因为我们经常会和窗口管理器打交道吧。 下面,我们来看看死锁的两个线程。 >> 请移步至 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
