当服务实例出现故障时,Nacos如何处理?
当服务实例出现故障时,Nacos的应对策略
在微服务架构日益盛行的今天,服务之间的稳定性与可靠性成为了我们架构师们不得不面对的重要课题。尤其是在面对服务实例出现故障时,如何确保整个系统的稳定运行,成为了我们首要考虑的问题。Nacos作为一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台,为我们提供了强大的解决方案。
一、Nacos的核心功能与服务故障的关系
在微服务架构中,服务之间的调用关系错综复杂,一个服务可能依赖于多个其他服务。当其中一个服务实例出现故障时,如果处理不当,很可能会导致整个系统的崩溃。Nacos通过提供动态服务发现、配置管理和服务管理等功能,帮助我们在微服务架构中应对服务故障。
动态服务发现:Nacos支持基于DNS和基于RPC的服务发现。服务提供者可以将自己的服务注册到Nacos,服务消费者可以通过Nacos订阅服务,获取服务提供者的地址列表。当服务实例出现故障时,Nacos可以实时感知并更新服务列表,确保服务消费者能够访问到健康的服务实例。
配置管理:Nacos提供了配置管理功能,支持配置的动态更新和推送。通过Nacos,我们可以将服务的配置信息存储在中心化的配置中心,实现配置的集中管理。当服务实例出现故障时,我们可以通过修改配置信息,快速定位并解决问题。
服务管理:Nacos提供了服务管理功能,包括服务的上下线、权重调整、负载均衡等。通过Nacos,我们可以对服务实例进行精细化管理,确保服务的稳定运行。
二、Nacos处理服务故障的策略
当服务实例出现故障时,Nacos会根据配置的降级策略对请求进行相应处理。这些策略包括快速失败、降级等。
快速失败策略(failfast):当服务实例出现故障时,Nacos会立即返回错误给服务消费者,而不是等待超时。这种策略可以迅速地将问题暴露给调用方,使其能够及时进行错误处理。同时,由于减少了不必要的等待时间,可以提高系统的响应速度。
降级策略(degrade):当服务实例出现故障时,Nacos会根据配置的降级规则自动处理请求。这些规则可以包括只返回部分数据、执行备份服务等。通过降级策略,我们可以在服务实例出现故障时,仍然为调用方提供一定的服务能力,确保系统的可用性。
除了上述策略外,Nacos还提供了丰富的服务治理功能,帮助我们更好地应对服务故障。例如,Nacos支持服务的熔断与限流,可以在服务实例出现故障时,自动熔断对该服务的调用,防止故障扩散。同时,Nacos还支持服务的负载均衡和容错处理,可以根据服务实例的健康状态和性能状况,自动调整请求的分发策略,确保系统的稳定运行。
三、如何配置Nacos以应对服务故障
要充分利用Nacos的功能来应对服务故障,我们需要合理配置Nacos的相关参数和策略。以下是一些建议:
配置合理的服务健康检查策略:Nacos支持基于TCP、HTTP和MySQL等多种健康检查方式。我们可以根据服务的实际情况选择合适的检查方式,并设置合理的检查间隔和超时时间。这样可以确保Nacos能够及时发现并处理服务实例的故障。
配置合理的降级策略:我们可以根据服务的特性和业务需求,配置合适的降级策略。例如,对于非关键性的服务,我们可以选择只返回部分数据或执行备份服务的降级策略;对于关键性的服务,我们可以选择熔断或限流的策略来防止故障扩散。
监控和告警:通过Nacos的监控和告警功能,我们可以实时了解服务的运行状况和性能数据。当服务实例出现故障时,Nacos可以自动触发告警通知,帮助我们及时发现并处理问题。
四、总结与展望
在微服务架构中,服务故障是不可避免的问题。然而通过合理配置和使用Nacos等优秀的服务治理平台我们可以有效地应对服务故障确保系统的稳定运行。未来随着微服务架构的不断发展新的技术和服务治理平台也将不断涌现。作为架构师我们需要不断学习和探索新的技术不断提升自己的能力以应对各种挑战。
相关文章:

当服务实例出现故障时,Nacos如何处理?
当服务实例出现故障时,Nacos的应对策略 在微服务架构日益盛行的今天,服务之间的稳定性与可靠性成为了我们架构师们不得不面对的重要课题。尤其是在面对服务实例出现故障时,如何确保整个系统的稳定运行,成为了我们首要考虑的问题。…...
遥感数据集制作(Potsdam数据集为例):TIF图像转JPG,TIF标签转PNG,图像重叠裁剪
文章目录 TIF图像转JPGTIF标签转PNG图像重叠裁剪图像重命名数据集转COCO格式数据集转VOC格式 遥感图像不同于一般的自然图像,由于波段数量、图像位深度等原因,TIF图像数据不能使用简单的格式转换方法。本文以Potsdam数据集为例,制作能够直接用…...

根据web访问日志,封禁请求量异常的IP,如IP在半小 时后恢复正常则解除封禁
在网络安全日益受到重视的今天,如何有效防范恶意流量和攻击成为了每个网站管理员必须面对的问题。恶意流量不仅会影响网站的正常运行,还可能导致服务器崩溃,给网站带来不可估量的损失。为了应对这一问题,我们特别推出了一款实用的…...
)
2.go语言初始(二)
本篇博客涉及到go 的基础数据类型、 go 语言中的运算符、转义字符、格式化输出、字符串操作 go 语言中的运算符 在 go 语言中,基本数据类型主要包括以下几类:整数类型、浮点数类型、复数类型、布尔类型、字符串类型、字节类型(byte…...

MQTT对比HTTP
吞吐量:根据3G网络的测量结果,MQTT的吞吐量比HTTP快93倍。这意味着在相同的网络条件下,MQTT能够更有效地传输数据,从而在处理大量数据或实时数据传输时具有更高的效率。架构与模式:MQTT基于发布/订阅模型,提…...
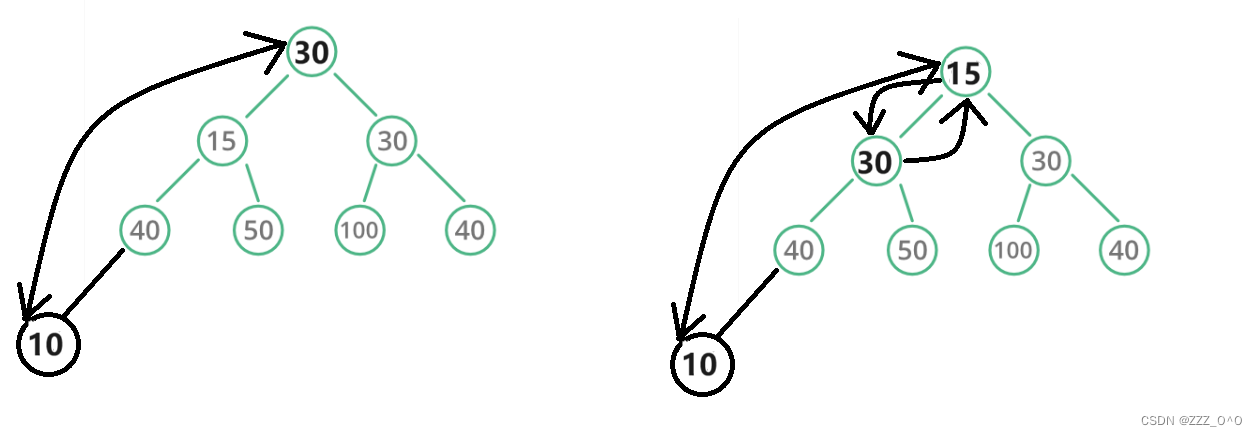
暴力数据结构之二叉树(堆的相关知识)
1. 堆的基本了解 堆(heap)是计算机科学中一种特殊的数据结构,通常被视为一个完全二叉树,并且可以用数组来存储。堆的主要应用是在一组变化频繁(增删查改的频率较高)的数据集中查找最值。堆分为大根堆和小根…...

死锁调试技巧:工作线程和用户界面线程
有人碰到了一个死锁问题,找到我们想请我们看看,这个是关于应用程序用户界面相关的死锁问题。 我也不清楚他为什么会找上我们,可能是因为我们经常会和窗口管理器打交道吧。 下面,我们来看看死锁的两个线程。 >> 请移步至 …...
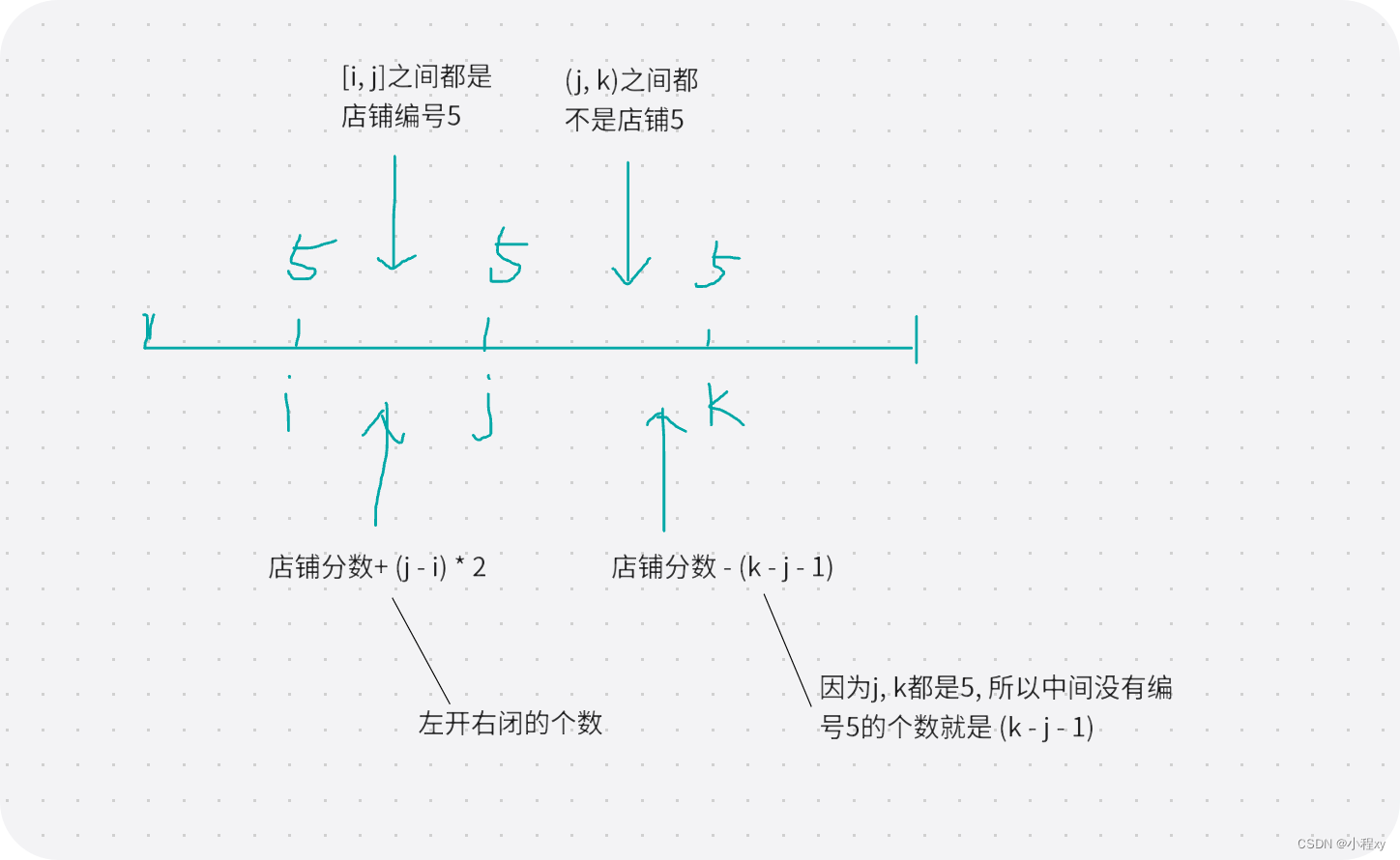
蓝桥杯-外卖店优先级(简单写法)
“饱了么”外卖系统中维护着 N 家外卖店,编号 1∼N。 每家外卖店都有一个优先级,初始时 (0 时刻) 优先级都为 0。 每经过 1 个时间单位,如果外卖店没有订单,则优先级会减少 1,最低减到 0;而如果外卖店有订…...

VueRouter使用总结
VueRouter 是 Vue.js 的官方路由管理器,用于构建单页面应用(SPA)。在使用 VueRouter 时,开发者可以定义路由映射规则,并在 Vue 组件中通过编程式导航或声明式导航的方式控制页面的跳转和展示。以下是 VueRouter 使用的…...
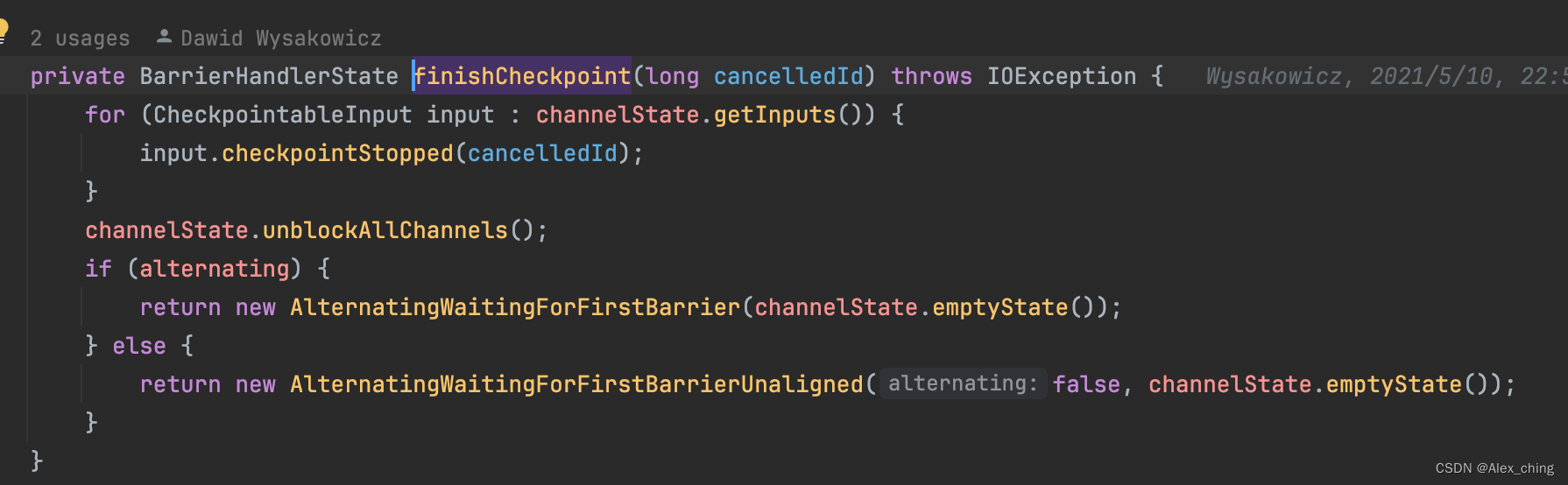
Flink checkpoint 源码分析- Checkpoint snapshot 处理流程
背景 在上一篇博客中我们分析了代码中barrier的是如何流动传递的。Flink checkpoint 源码分析- Checkpoint barrier 传递源码分析-CSDN博客 最后跟踪到了代码org.apache.flink.streaming.runtime.io.checkpointing.CheckpointedInputGate#handleEvent 现在我们接着跟踪相应…...
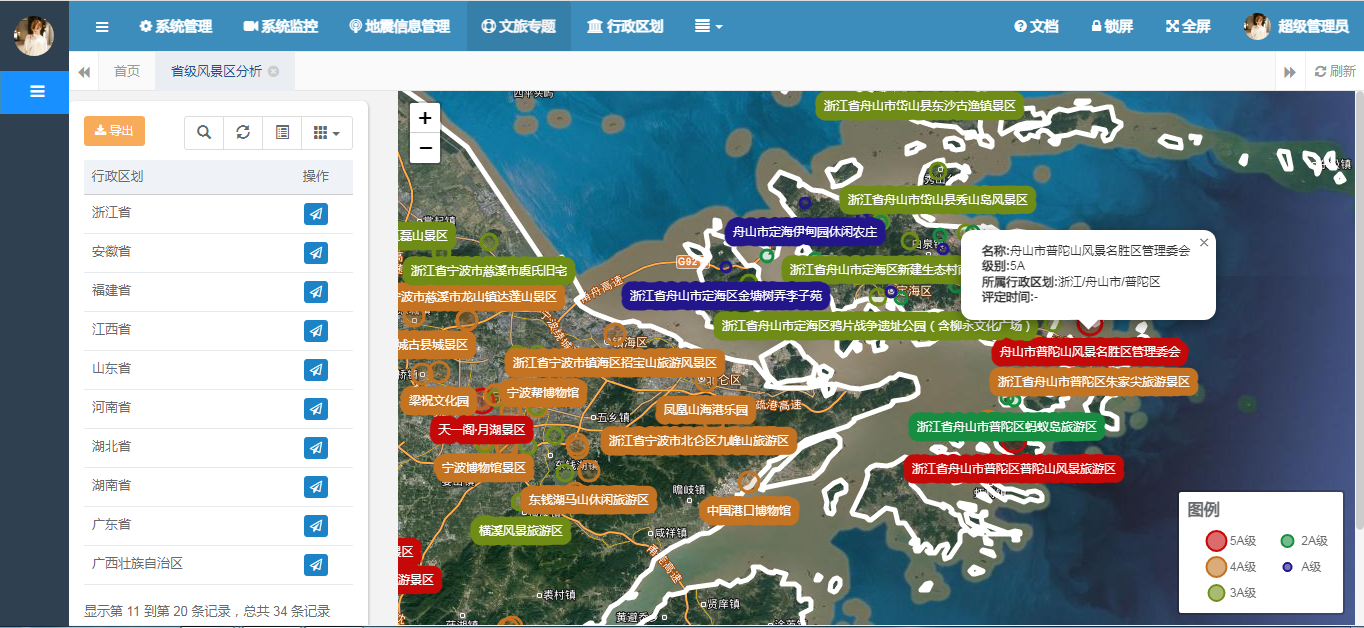
Leaflet.canvaslabel在Ajax异步请求时bindPopup无效的解决办法
目录 前言 一、场景重现 1、遇到问题的代码 2、问题排查 二、通过实验验证猜想 1、排查LayerGroup和FeatureGroup 2、排查Leaflet.canvaslabel.js 三、柳暗花明又一村 1、点聚类的办法 2、歪打正着 总结 前言 在上一篇博客中介绍了基于SpringBoot的全国风景区WebGIS按…...

Go 处理错误
如果你习惯了 try catch 这样的语法后,会觉得处理错误真简单,然后你再来接触 Go 的错误异常,你会发现他好复杂啊,怎么到处都是 error,到处都需要处理 error。 首先咱们需要知道 Go 语言里面有个约定,就是一…...

python读取excel数据写入mysql
概述 业务中有时会需要解析excel中的数据,按照要求处理后,写入到db中; 用python处理这个正好简便快捷 demo 没有依赖就 pip install pymysql一下 import pymysql from pymysql.converters import escape_string from openpyxl import loa…...
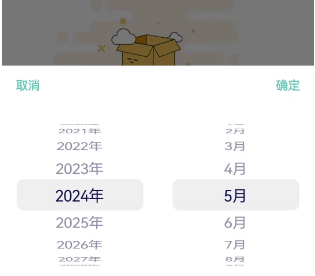
flutter日期选择器仅选择年、月
引入包:flutter_datetime_picker: 1.5.0 封装 import package:flutter/cupertino.dart; import package:flutter/material.dart; import package:flutter_datetime_picker/flutter_datetime_picker.dart;class ATuiDateTimePicker {static Future<DateTime> …...

素数筛详解c++
一、埃式筛法 代码 二、线性筛法(欧拉筛法) 主要的思想就是一个质数的倍数(倍数为1除外)肯定是合数,那么我们利用这个质数算出合数,然后划掉这个合数,下次就可以不用判断它是不是质数,节省了大量的时间。 …...
【Python超详细的学习笔记】Python超详细的学习笔记,涉及多个领域,是个很不错的笔记
获取笔记链接 Python超详细的学习笔记 一,逆向加密模块 1,Python中运行JS代码 1.1 解决中文乱码或者报错问题 import subprocess from functools import partial subprocess.Popen partial(subprocess.Popen, encodingutf-8) import execjs1.2 常用…...
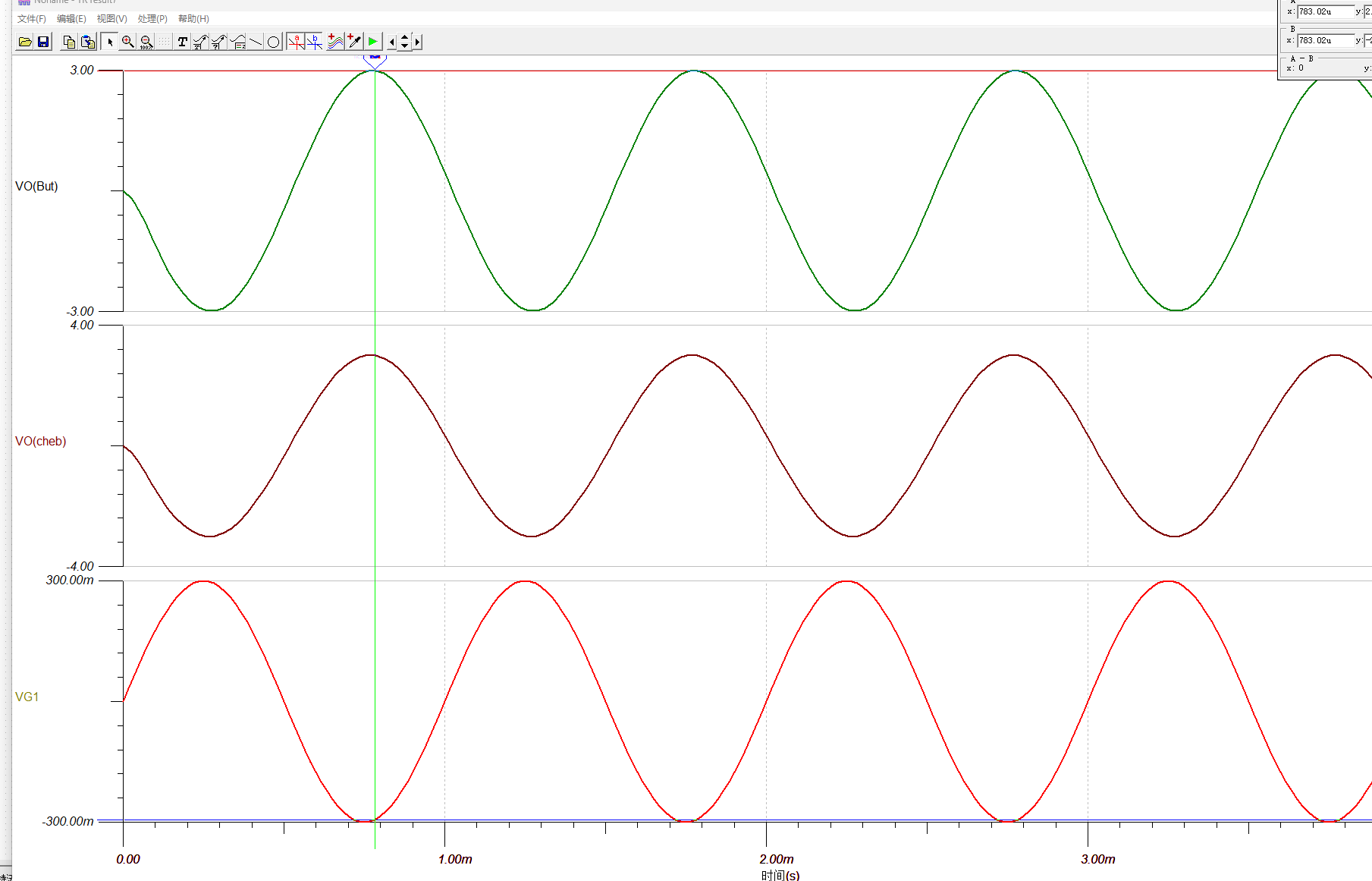
TINA 使用教程
常用功能 分析-电气规则检查:短路,断路等分析- 直流分析 交流分析 瞬态分析 视图-分离曲线 由于输出的容性负载导致的振荡 增加5欧电阻后OK 横扫参数 添加横扫曲线的电阻,选择R3:8K-20K PWL和WAV文件的支持 示例一:…...
weblogic 任意文件上传 CVE-2018-2894
一、漏洞简介 在 Weblogic Web Service Test Page 中存在一处任意文件上传漏洞, Web Service Test Page 在"生产模式"下默认不开启,所以该漏洞有一定限制。利用该 漏洞,可以上传任意 jsp 文件,进而获取服务器权限。 二…...

我的第一个网页:武理天协
1. html代码 1.1 首页.html <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><title>武理天协</title><link rel"stylesheet" href"./style.css"><link rel"stylesh…...
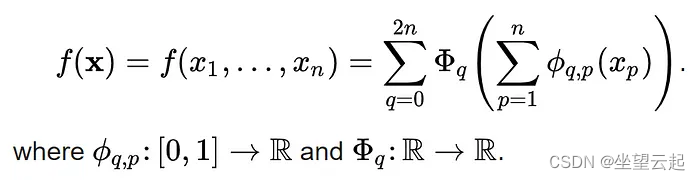
机器学习笔记 KAN网络架构简述(Kolmogorov-Arnold Networks)
一、简述 在最近的研究中,出现了号称传统多层感知器 (MLP) 的突破性替代方案,重塑了人工神经网络 (ANN) 的格局。这种创新架构被称为柯尔莫哥洛夫-阿诺德网络 (KAN),它提出了一种受柯尔莫哥洛夫-阿诺德表示定理启发的函数逼近的方法。 与 MLP 不同,MLP 依赖于各个节…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
