three.js能实现啥效果?看过来,这里都是它的菜(06)
这是第五期了,本期继续分享three.js可以实现的3D动画案例,有老铁反馈再发案例的时候,是否可以顺道分享一下three.js的知识点,好吧,安排。
材质动画
材质动画可以实现各种复杂的视觉效果,包括但不限于以下几种:
1. 纹理变形动画:
通过修改纹理坐标或者纹理采样算法,可以实现纹理的扭曲、拉伸、波动等效果,从而呈现出纹理变形的动画效果,比如水面波纹、火焰的燃烧等效果。

2. 颜色渐变动画:
通过修改材质的颜色属性,可以实现颜色的渐变、闪烁、渐变等效果,从而呈现出颜色变化的动画效果,比如日落时的天空颜色变化、闪烁的灯光效果等。
3. 光照效果动画:
通过修改材质的光照属性,可以实现光照效果的动画,比如模拟阳光穿过树叶的效果、光影的移动等。

4. 多重纹理叠加动画:
通过在着色器中叠加多个纹理,并通过修改纹理坐标或者混合模式,可以实现多重纹理叠加的动画效果,比如地面上的草地和花朵的飘动效果。

5. 材质反射和折射动画:
通过修改材质的反射和折射属性,可以实现材质表面的反射和折射效果的动画,比如水面的波纹折射效果、镜面的反射效果等。

材质动画可以实现的效果非常丰富,通过对ShaderMaterial中的uniform变量进行动态修改,可以实现各种复杂的视觉效果,为场景渲染增添了更多的可能性。

相关文章:

three.js能实现啥效果?看过来,这里都是它的菜(06)
这是第五期了,本期继续分享three.js可以实现的3D动画案例,有老铁反馈再发案例的时候,是否可以顺道分享一下three.js的知识点,好吧,安排。 材质动画 材质动画可以实现各种复杂的视觉效果,包括但不限于以下…...

利用ESP32-C3将TF卡内容变成U盘进行读取
利用ESP32-C3将TF卡内容变成U盘进行读取 ESP32-C3是一款高性价比的微控制器,具备WiFi和蓝牙功能,广泛应用于物联网(IoT)项目中。除了常见的无线通信功能外,ESP32-C3还可以用来模拟U盘读取TF卡内容。本文将介绍如何通过…...

C++小病毒
C小病毒(注:对电脑无过大伤害) 短短行,创造奇迹! 把这个文件命名为virus.exe就可以使用了。 #include<bits/stdc.h> #include<windows.h> using namespace std; int main() {HWND hwnd GetForegroundW…...

使用VUE3+TS+elementplus创建一个增加按钮
一、前言 在上一篇文章中分享了创建table的过程,详见(VUE3TSelementplus创建table,纯前端的table),本文在创建好的table的基础上,再创建一个增加按钮。 二、程序展示 1、前面创建table的程序 <templ…...
)
Python面试宝典:文件读写和上下文管理器以及输入输出流面试题(1000加python面试题助你轻松捕获大厂Offer)
Python面试宝典:1000加python面试题助你轻松捕获大厂Offer【第一部分:Python基础:第八章:文件操作和输入输出:第一节:文件读写和上下文管理器以及输入输出流】 第八章:文件操作和输入输出第一节:文件读写和上下文管理器以及输入输出流1.1、文件读写基本操作1.1.1、打开…...

Spring Boot | Spring Boot 实现 “记住我“ 功能
目录: 一、SpringBoot 中 自定义 "用户授权管理" ( 总体内容介绍 )二、实现 "记住我" 功能 ( 通过 "HttpSecurity类" 的 rememberMe( )方法来实现 "记住我" 功能 ) :2.1 基于 "简单加密 Token" 的方式 ( 实现 "记住我&…...

AGM AG32 MCU替代GD32F407/STM32F407的手持示波器方案
一、AG32 MCU替代GD32F407/STM32F407的数字示波器方案 市场上有多款数字迷你示波器,特别小巧,携带非常方便。单通道,标注100Mhz带宽,500MS采样率。 这样高的采样率需要使用高速AD及很高性能的处理器。原方案使用AD9288双通道8bit …...

MongoDB基础入门到深入(八)MongoDB整合SpringBoot、Chang Streams
文章目录 系列文章索引十五、MongoDB整合SpringBoot1、环境准备2、集合操作3、文档操作(1)相关注解(2)创建实体(3)添加文档(4)查询文档(5)更新文档࿰…...
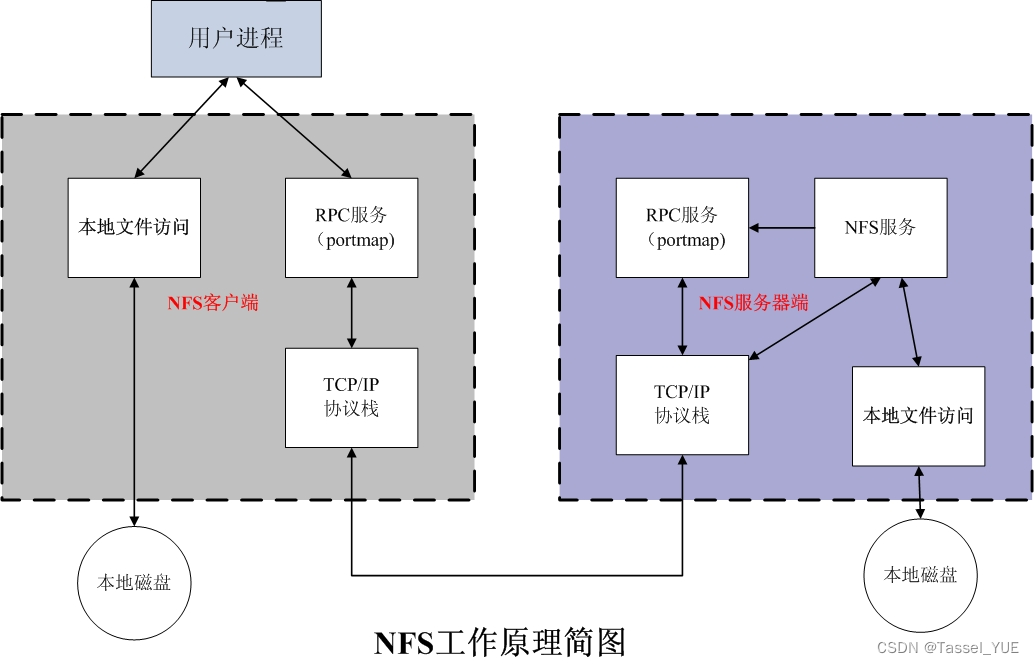
linux下的nfs概述与实验(openEuler22.03)
目录 什么是NFSNFS工作原理NFS常用文件/etc/exports文件/etc/exports格式 /var/lib/nfs/etab文件 NFS常用选项NFS配置方式1. 安装NFS和RPC2. 启动rpcbind和nfs3. 准备目录4. 配置/etc/exports并重启服务5. 连接测试服务端自我测试客户端测试 补充常用命令永久挂载注意 什么是NF…...

影响Oracle数据库打开速度的因素
当Oracle发起一个事务需要更改数据时,如果所涉及的数据块不在BUFFER CACHE中,那么Oracle服务进程首先会将相关数据块从数据文件中读进BUFFER CACHE进行更改(直接路径读除外),更改后的数据块称之为脏块(DIRT…...
dify:开源 LLMOps平台。
单纯笔记: 一、关于 Dify dify/README_CN.md at main langgenius/dify GitHub Dify 是一款开源的大语言模型(LLM)应用开发平台。它融合了后端即服务(Backend as Service)和 LLMOps 的理念,使开发者可以…...

CCF20220601——归一化处理
CCF20220601——归一化处理 代码如下: #include<bits/stdc.h> using namespace std; int main() {int n,a[1000],sum0;scanf("%d",&n);for(int i1;i<n;i){scanf("%d",&a[i]);suma[i];}double aver1.0,b0.0,d1.0;aversum/(n*1…...

用Ai编写一个电机驱动程序
问:帮我写一个步进电机的控制程序,要有包括加减速,以及电机步中断处理函数。 答:编写一个步进电机的控制程序涉及到硬件层面的操作,通常需要依赖特定的硬件平台和相应的驱动程序。以下是一个简化的示例,它展…...

【C++入门】—— C++入门 (下)_内联函数
前言:在了解完前面的C基础内容后,马上我们就要真正不如C的学习了,但在之前让我们最后了解最后一点点C入门知识!来迟的520特别篇! 本篇主要内容: 内联函数 auto关键字 范围for 指针空值nullptr C入门 1. 内联…...
)
Java数据结构与算法(最小栈)
前言 设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。i…...
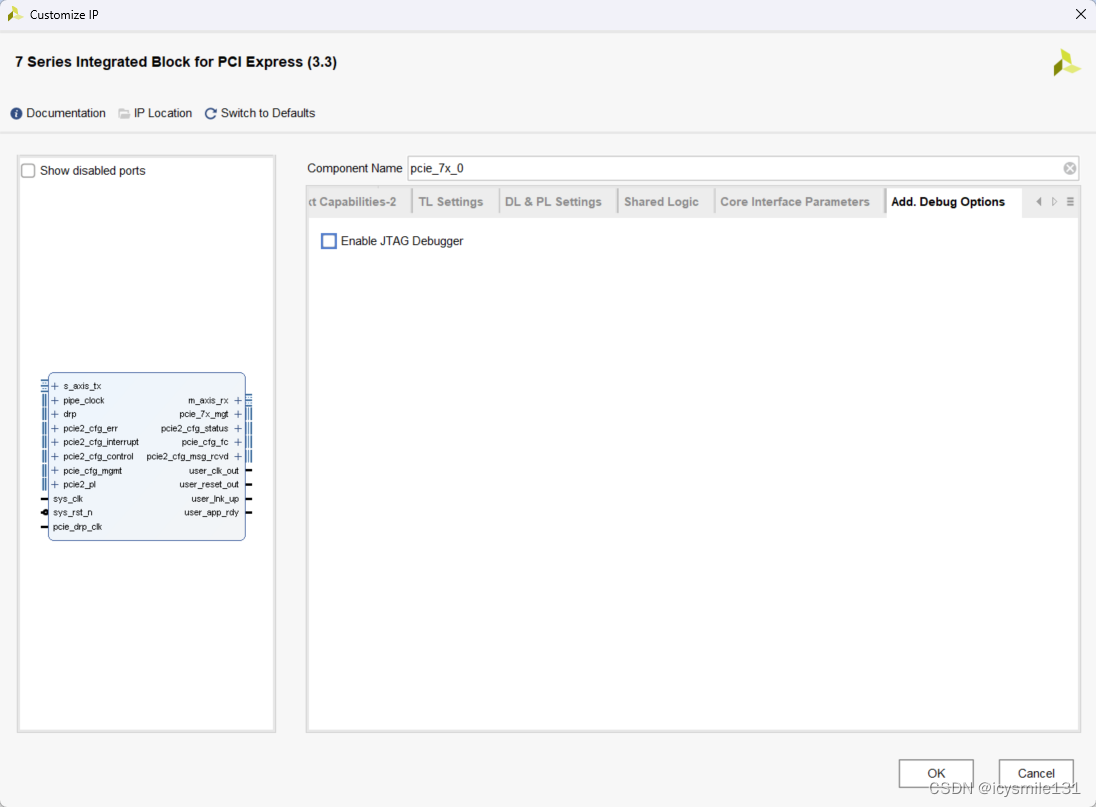
7 Series FPGAs Integrated Block for PCI Express IP核 Advanced模式配置详解(三)
1 TL Settings Transaction Layer (TL)设置只在Advanced模式下有效。 Endpoint: Unlock and PME_Turn_Off Messages: 与端点的电源管理相关,允许发送解锁和电源管理事件关闭消息。 Root Port: Error Messages: Error Correctable(错误可纠正)…...

k8s 部署mqtt简介
在Kubernetes(K8s)中部署MQTT(Message Queuing Telemetry Transport)服务通常涉及以下几个步骤: 选择MQTT Broker MQTT Broker是MQTT消息传递的中间件。流行的MQTT Broker包括Mosquitto, HiveMQ, EMQ X等。你需要选择一…...

汇凯金业:量化交易中常用的数学模型有哪些
量化交易中运用了多种数学模型来识别市场的潜在机会和建立交易策略。以下是一些在量化交易中常用的数学模型: 1. 时间序列分析模型 时间序列分析是研究和预测数据点随时间顺序变化趋势的方法。在量化交易中,常用的时间序列模型包括: 自回归&a…...

局部直方图均衡化去雾算法
目录 1. 引言 2. 算法流程 3. 代码 4. 去雾效果 1. 引言 局部直方图算法是一种基于块的图像去雾方法,它将图像分割为若干个块,并在每个块内计算块的局部直方图。通过对各个块的直方图进行分析和处理,该算法能够更好地适应图像中不同区域的…...

selenium环境安装和web自动化基础
webUI自动化背景 因为web页面经常会变化,所以UI自动化测试的维护成本很高。不如接口的适用面广,所以大部分公司会做接口自动化测试,但是未必会做UI自动化测试; UI自动化测试要做也是覆盖冒烟测试,不会到很高的覆盖率&a…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
