二.常见算法--贪心算法
(1)单源点最短路径问题
问题描述:
给定一个图,任取其中一个节点为固定的起点,求从起点到任意节点的最短路径距离。
例如: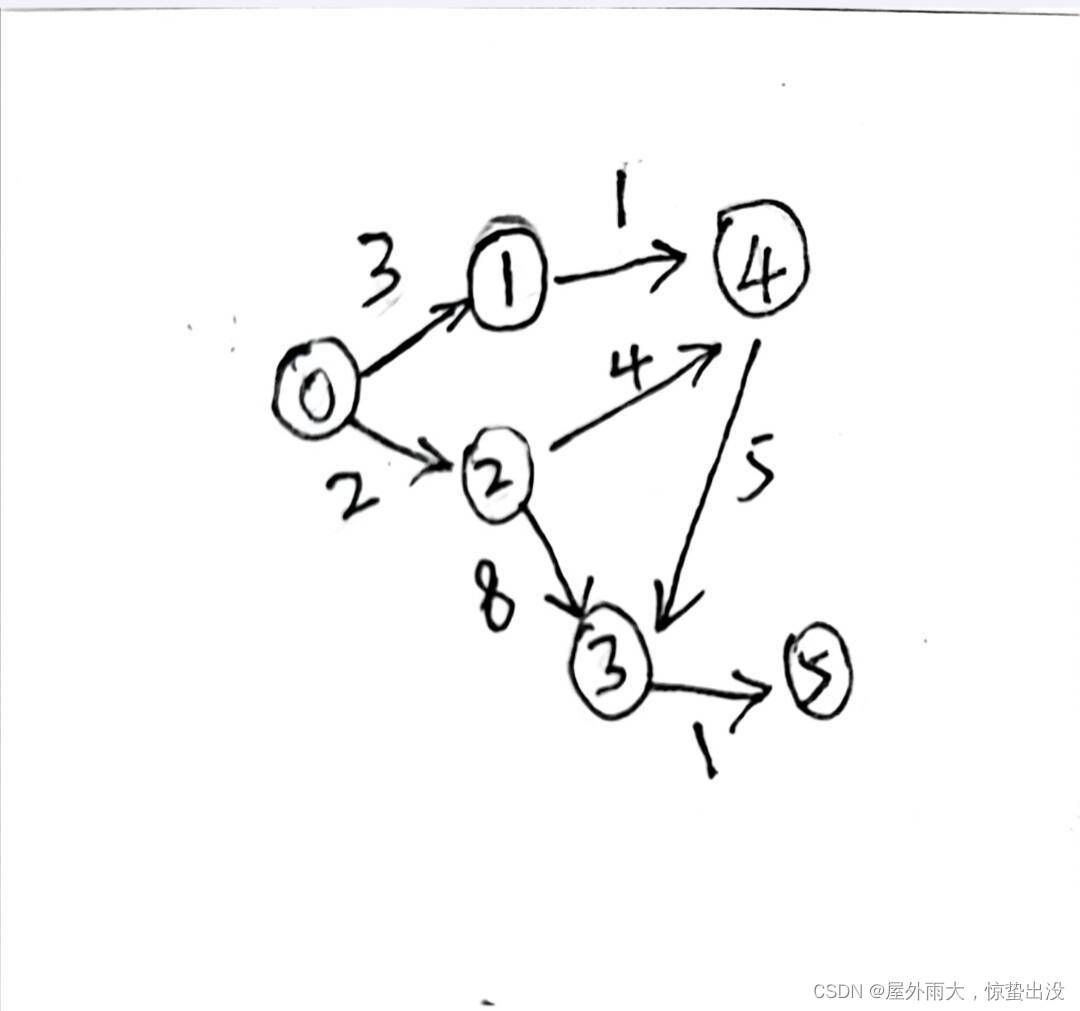
思路与关键点:
以下代码中涉及到宏INT_MAX,存在于<limits.h>中。

首先,建立三个数组dist,S,W,prev分别用来存储从起始节点到任意节点的最短距离;相对于s距离起点的最短路径节点集合;存储要遍历的图的各条边的距离;用来存储各个节点的直接前驱节点。
3个主要的个功能函数。
(1)minDistance函数用来寻找V-S集合中的距离起点的最短距离,并返回该节点的下标。
(2)dijkstra函数用来寻找从起始节点到任意节点的最短路径长度。
思路是把节点分为两类,一类是没有放进S集合中的节点,一类是已经放进去的节点。那么,寻找从起始节点到节点v的最短路径就有两种可能的取值。
第一种是组成该最短路径的就是dist[v]。
第二种是新加入S集合的节点u可能会组成一个新的更短的路径,这时,要更新dist[v]。
(3)Traceback函数用来打印从源点到终点的路径。这个函数基于prev数组,该数组建立的核心原理是:每次更新dist数组,一定是因为s集合中增加了一个节点u,这个u一定是当前更新dist[v]的直接前驱节点。递归调用,不断找前一个前驱节点,就可以打印出完整路径了。
伪代码:

代码:
#include <iostream>
#include <limits.h>using namespace std;
#define V 6 // 节点的数量void Traceback(int v, int i, int prev[]);int minDistance(int dist[], int S[]);void printSolution(int dist[]);void dijkstra(int W[V][V], int src);int main() {int W[V][V] = {{0, 3, 2, 0, 0, 0},{0, 0, 0, 0, 1, 0},{0, 0, 0, 8, 4, 0},{0, 0, 0, 0, 0, 1},{0, 0, 0, 5, 0, 0},{0, 0, 0, 0, 0, 0}};dijkstra(W, 0);//起始节点为节点 0 return 0;}
// 找到距离数组中最小值的索引
int minDistance(int dist[], int S[]) {int min = INT_MAX, min_index;for (int j = 0; j < V; j++) {/*如果节点j没有包含在最短路径数组中,初始时,只要有路径,就更新最短路径数组的值。后面,每次进入循环都与当前的最短距离进行比较,更新。找到V(全部节点集合)-S(已找到的最短路径节点集合)中距离起点最短的路径的节点编号。 */ if (S[j] == 0 && dist[j] <= min) {min = dist[j];min_index = j;}}return min_index;
}// 打印最终的最短路径
void printSolution(int dist[]) {printf("节点\t最短距离\n");for (int i = 0; i < V; i++)printf("%d\t%d\n", i, dist[i]);
}// Dijkstra算法的实现
void dijkstra(int W[V][V], int src) {int dist[V]; // 存储从源节点到每个节点的最短距离int S[V]; // 记录节点是否已经包含在已找到的最短路径节点集合中int prev[V];// 初始化所有距离为无穷大,标记所有节点为未包含for (int i = 0; i < V; i++) {dist[i] = INT_MAX;S[i] = 0;}// 设置起始节点的距离为0dist[src] = 0;// 找到最短路径for (int count = 0; count < V - 1; count++) {// 选择距离最小的节点int u = minDistance(dist, S);// 标记节点为已包含S[u] = 1;// 更新相邻节点的距离for (int v = 0; v < V; v++) {/*如果该节点没有包含在最短路径数组中,有路径可直接到达该节点,并且有路径可达该节点,并且,从节点0到节点u的最短路径长度,与,从节点u到节点v的路径距离之和小于从节点0到该节点当前最短距离,则更新最短距离。 */ if (!S[v] &&W[u][v] && dist[u] != INT_MAX &&dist[u] +W[u][v] < dist[v]) {dist[v] = dist[u] + W[u][v];prev[v]=u;}}}// 打印最终的最短路径printSolution(dist);int v,i;printf("请输入源点及终点");cin>>v>>i;printf("从源点%d到终点%d的最短路径为:\n",v,i);Traceback(v,i,prev);
}
//输出最短路径 v源点,i终点,
void Traceback(int v, int i, int prev[])
{// 源点等于终点时,即找出全部路径if (v == i){cout << i;return;}Traceback(v, prev[i], prev);cout << "->" << i;
}运行结果:
关键步骤证明:
时间复杂度与空间复杂度:
时间复杂度为0(
),空间复杂度为0(
)。
(2)活动选择问题
问题描述:
假定有一个n个活动的集合S={a1,a2,……,an},这些活动使用同一个资源,而这个资源在某个时刻只能供一个活动使用。每个活动有一个开始时间si和一个结束时间fi,其中0<=si<fi<∞。如果被选中,任务ai发生在半开时间区间[si,fi)期间。如果两个活动ai和aj满足[si,fi)和[sj,fj)不重叠,则称他们是兼容的.也就是说,若si>=fj或sj>=fi,则ai和aj是兼容的。
在活动选择问题中,我们希望选出一个最大兼容活动集。
例子: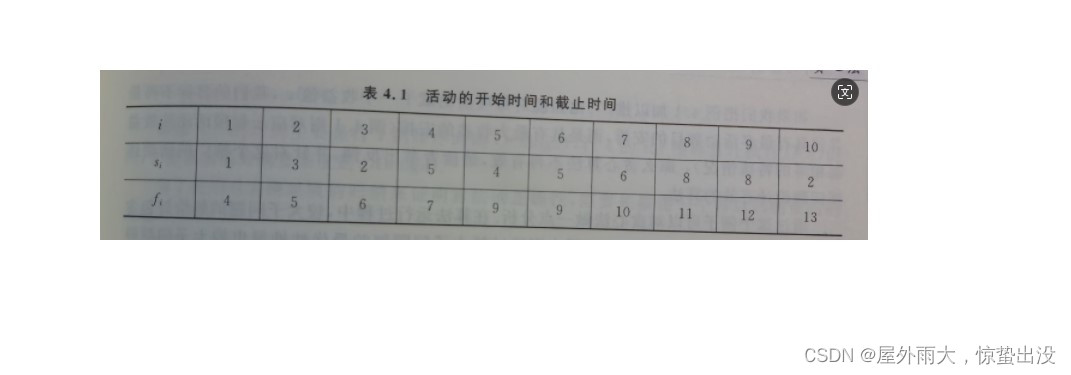
该活动序列的最大兼容活动集为1,4,8或1,4,9
思路与关键点:
按活动结束时间从小到大排序
每次选择的活动将作为是否与下一个活动兼容的判断依据。
伪代码:

代码:
#include<iostream>
#include<string.h>
using namespace std;
void Traceback(int Trace[],int n);
void sort(int n,int *s,int* f)
{int a,b,i,j;//冒泡排序,按结束时间从小到大排列活动 for(i=1;i<n;i++){for(j=1;j<n-i+1;j++){if(f[j]>f[j+1]){a=f[j];f[j]=f[j+1];f[j+1]=a;b=s[j];s[j]=s[j+1];s[j+1]=b;}}}
}
int GreedySelect(int n,int s[],int f[],bool A[])
{int Trace[n];Trace[1]=1;A[1]=true;//第一个活动必然在最优解中 int j=1,count=1; //从第二个活动开始,寻找下一个兼容的活动 for(int i=2;i<=n;i++){if(s[i]>=f[j]){A[i]=true;j=i;//将已经选人的最后一个活动标号作为下一次比较兼容的参照 count++;Trace[count]=i;}else A[i]=false;} Traceback(Trace,count);return count;
}
//打印的活动序列是按照结束时间从小到大排好序的活动序列,而不是原来的活动序列 void Traceback(int Trace[],int n){printf("活动安排顺序为:");for(int i=1;i<=n;i++){cout<<"->"<<Trace[i];}cout<<endl;}
int main(){int n,s[50],f[50];bool A[50];memset(A,false,sizeof(A)); printf("请输入活动个数:\n"); cin>>n;//活动标号与数组下标保持一致,从1开始标号 for(int i=1;i<=n;i++){printf("请输入第%d个活动的开始时间和结束时间\n",i);cin>>s[i]>>f[i];printf("第%d个活动的开始时间是%d,结束时间是%d\n",i,s[i],f[i]);} sort(n,s,f);printf("最多相容活动数为:\n");cout<<GreedySelect(n,s,f,A)<<endl;return 0;
}运行结果:
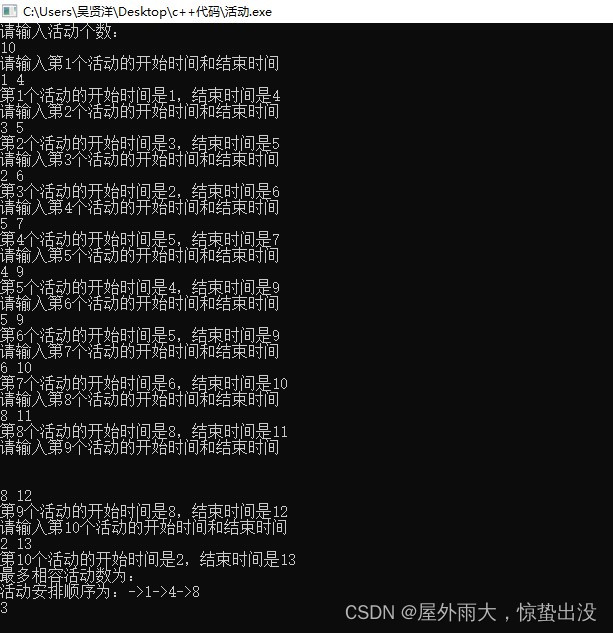
关键步骤证明:

时间复杂度与空间复杂度:
时间复杂度主要为排序花的时间为0(
),如果换成其他排序可以降低时间复杂度,空间复杂度为0(n)
(3)最小生成树--prim算法实现
问题描述:
给定一个图,求出其最小生成树
最小生成树定义
对于一个带权(假定每条边上的权值均为大于零的实数)连通无向图G中的不同生成树,各树的边上的权值之和可能不同;图中所有生成树中具有边上的权值之和最小的树称为该图的最小生成树.按照生成树的定义,n个顶点的连通图的生成树有n个顶点和(n-1)条边.因此构造最小生成树的准则有三条:
(1) 必须只使用该图中的边来构造最小生成树;
(2) 必须使用且仅使用(n-1)条边来连接图中的n个顶点;
(3) 不能使用产生回路的边.
思路与关键点:
首先,这里有一个头文件<alogrithmn>,里面包含了丰富实用的函数,非常nice。这里使用到了其中的fill函数和min函数。分别用来填充数组和求最小值的。建立一个数组used,记录哪些没有进入最小生成树的集合,每次不断地将没有加入used中的距离加入used数组的节点 权值最小的节点加入used数组。 更新V轮mincost数组,得到最小生成树。
伪代码:

代码:
#include<iostream>
#include<algorithm>
#define MAX_V 100
#define INF 1000
using namespace std; int main()
{int V,E;int i,j,m,n;int cost[MAX_V][MAX_V];//存储每个节点之间的权值 int mincost[MAX_V];//记录那些已经进入最小生成树的节点之间的权值 bool used[MAX_V];//用于判断是否已经进入最小生成树,false表示否,true表示是 printf("请输入节点个数与边数\n"); cin>>V>>E;int Trace[V];fill(mincost,mincost+V+1,INF);//最小生成树一共有V个节点,V+1条边 fill(used,used+V,false);//一共有V个节点 //初始化cost[] for(i=0;i<V;i++){for(j=0;j<V;j++){if(i==j) cost[i][j]=0;//节点自己到自己权值为0 else cost[i][j]=INF; }}//向cost[]里面填充各个节点之间的权值 for(m=0;m<E;m++){printf("请输入两个端点以及它们之间边的权值\n");cin>>i>>j>>cost[i][j];cost[j][i]=cost[i][j];//无向图,中心对称 }mincost[0]=0; int res=0;//存储最终的最小生成树权值和 int count=0;/*遍历图,不断地将没有加入used中的距离加入used数组的节点权值最小的节点加入used数组。
更新V轮mincost数组,得到最小生成树。 */while(true)//也可以写成for(int i=0;i<V;i++) {int v=V;for(m=0;m<V;m++){ if((!used[m])&&(mincost[m]<mincost[v]))v=m; }Trace[count]=v;count++; if(v==V) break;Trace[count]=v;//最后一个跳出来了,没记录,要把最后一个节点加入 used[v]=true;res+=mincost[v];for(m=0;m<V;m++){/*取(新加入最小生成树的节点到其他节点的权值)和记录在mincost中的到其他节点的权值进行比较,取它们之间的最小值,来更新mincost数组*/ mincost[m]=min(mincost[m],cost[v][m]); }}printf("最小生成树权值是:\n");cout<<res<<endl;printf("依次找到的节点是:\n");for(int i=0;i<V;i++){cout<<"->"<<Trace[i];}cout<<endl;
}运行结果:
输入上面单源点最短路径所示的图,运行结果如下
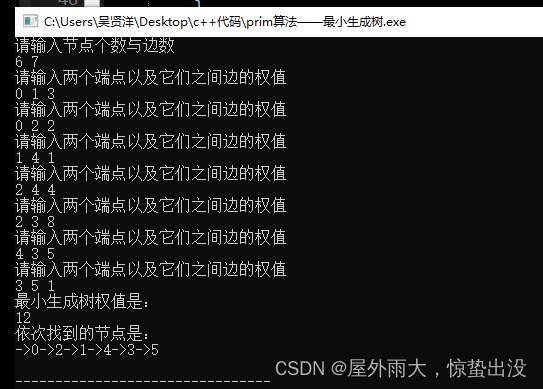
关键步骤证明:
视频证明
时间复杂度与空间复杂度:
时间复杂度与空间复杂度都是0()
友情链接:贪心算法
相关文章:
二.常见算法--贪心算法
(1)单源点最短路径问题 问题描述: 给定一个图,任取其中一个节点为固定的起点,求从起点到任意节点的最短路径距离。 例如: 思路与关键点: 以下代码中涉及到宏INT_MAX,存在于<limits.h>中…...
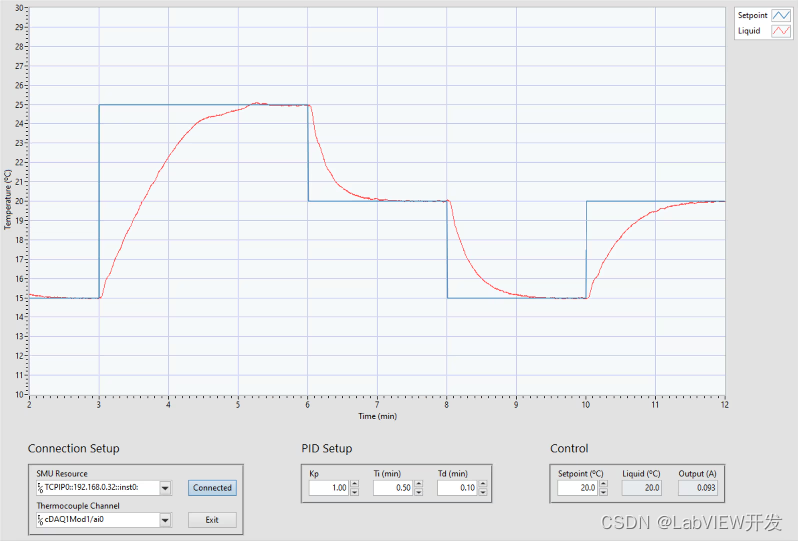
LabVIEW高温往复摩擦测试系统中PID控制
在LabVIEW开发高温往复摩擦测试系统中实现PID控制,需要注意以下几个方面: 1. 系统建模与参数确定 物理模型建立: 首先,需要了解被控对象的物理特性,包括热惯性、摩擦系数等。这些特性决定了系统的响应速度和稳定性。实验数据获取…...

配置yum源
以下是在 Linux 系统中配置新的 yum 源的一般步骤和命令示例(以 CentOS 系统为例): 备份原有 yum 源配置文件:mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.bak 创建新的 yum 源配置文件(…...
数据技术篇之数据同步)
深入理解数仓开发(二)数据技术篇之数据同步
1、数据同步 数据同步我们之前在数仓当中使用了多种工具,比如使用 Flume 将日志文件从服务器采集到 Kafka,再通过 Flume 将 Kafka 中的数据采集到 HDFS。使用 MaxWell 实时监听 MySQL 的 binlog 日志,并将采集到的变更日志(json 格…...
—— 类与对象(二))
C++语言学习(六)—— 类与对象(二)
目录 一、对象数组 二、对象指针 三、this 指针 四、类类型作为参数类型的三种形式 4.1 对象本身作为参数 4.2 对象指针作为参数 4.3 对象引用作为参数 五、静态成员 5.1 静态数据成员 5.2 静态成员函数 六、友元机制 6.1 友元函数 6.2 友元类 七、类的组合 八、…...

3d选择模型后不能旋转什么原因?怎么解决?---模大狮模型网
在3D建模和渲染的过程中,旋转模型是常见的操作。然而,有时在选择了模型后,却发现无法进行旋转,这可能会让许多用户感到困扰。本文将探讨3D选择模型后不能旋转的可能原因,并提供相应的解决方法。 一、3D选择模型后不能旋…...

从入门到精通:详解Linux环境基础开发工具的使用
前言 在这篇文章中,我将深入学习和理解Linux环境基础开发工具的使用。无论你是初学者还是有一定经验的开发者,相信这篇文章都会对你有所帮助。我们将详细讲解软件包管理器、编辑器、编译器、调试器、自动化构建工具以及版本控制工具的使用。 Linux软件…...
安装 node)
linux(centos 7)安装 node
linux(centos 7)安装 node 下载对应版本&安装解压配置环境变量使配置文件生效验证是否安装成功附加 目前node最新版本是 node-v22.0.0 官网下载地址:https://registry.npmmirror.com/binary.html?pathnode/latest-v22.x/node-v22.0.0-li…...

C++之第九课
课程列表 今天,我们要学习一种结构:循环结构。 循环的方法有3种。 今天先将第1种for学了: int a;//循环变量 int b; for(a1;a<10;a){//像if那样“打包”cout<<a<<" ";b; } 当然,也可以这样写&#…...

618精选编程书单推荐:优质知识提升你的代码力
前言 在这个快速发展的技术时代,不断学习和提升自己的编程技能是每位程序员的必修课。今天,我为大家精心挑选了一系列编程技术书籍,它们将是你技术成长道路上的宝贵财富。 文章目录 前言编程之路:为何阅读书籍是不可或缺的书籍的…...

使用httpx异步获取高校招生信息:一步到位的代理配置教程
概述 随着2024年中国高考的临近,考生和家长对高校招生信息的需求日益增加。了解各高校的专业、课程设置和录取标准对于高考志愿填报至关重要。通过爬虫技术,可以高效地从各高校官网获取这些关键信息。然而,面对大量的请求和反爬机制的挑战&a…...

使用Java Stream API的map方法将包含Long类型ID的流转换为String数组
在这个例子中,idList是一个包含Long类型ID的列表。我们使用stream()方法创建一个流,然后应用map(String::valueOf)方法将Long类型的ID转换为String类型。最后,我们使用toArray(String[]::new)方法将流中的元素收集到一个新的String[]数组中。…...

centos 安装nginx 并配置https ssl
进入你要安装的目录 一般是/usr/local/ wget https://nginx.org/download/nginx-1.24.0.tar.gz解压安装包:使用以下命令解压下载的Nginx安装包: tar -zxvf nginx-1.24.0.tar.gz在编译和安装Nginx之前,确保您的系统上已安装了必要的编译工具和…...

Jenkins 自动化部署
Post Steps部分 Exec cmmand cd /data/build/test-admin/ rm -f app.jar rm -f Dockerfile cp target/app.jar ./ cp docker/Dockerfile ./docker build -t test-admin . docker tag test-admin 192.168.1.100/test/test-admin:1.2-SNAPSHOT docker push 192.168.1.100/test/…...

VUE3好看的酒网站模板源码
文章目录 1.设计来源1.1 首页界面1.2 十大名酒界面1.3 名酒新闻界面1.4 联系我们界面1.5 在线留言界面 2.效果和结构2.1 动态效果2.2 代码结构 3.VUE框架系列源码4.源码下载 作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/detai…...

索引压缩技术详解
在现代搜索引擎和信息检索系统中,索引压缩技术是提高存储效率和检索速度的关键手段。本文将深入探讨几种常见的索引压缩技术,包括词典压缩、倒排列表压缩算法、文档编号重排序以及静态索引裁剪。 词典压缩 1.1 基础概念 词典(Dictionary&am…...

完全匹配企业需求的替代FTP升级软件怎么找
企业在处理数据传输时,效率和安全性是关键。尽管传统的FTP曾被广泛采用,但因其传输慢、安全性不足和难以管理等问题,已不再满足现代企业的需求。许多企业正在寻找能够满足其需求的FTP替代方案,但市场上选择众多,找到合…...

动态规划:分割等和子集
参考资料:代码随想录 题目链接:. - 力扣(LeetCode) 这道题是01背包问题的抽象,这道题的难点在于怎么绕明白遍历顺序是从后往前。 题目中给的nums数组,以nums[1,5,11,5]为例,可以分析为有4个物…...

踩坑——纪实
开发踩坑纪实 1 npm安装1.1 查看当前的npm镜像设置1.2 清空缓存1.3 修改镜像1.4 查看修改结果1.5 重新安装vue 2 VScode——NPM脚本窗口找不到3 springboot项目中updateById()失效4 前端跨域4.1 后端加个配置类4.2 CrossOrigin注解 5 路由出口6 springdoc openapi3 swagger3文件…...
)
java实现websocket的五种方式(mark下)
java实现websocket的五种方式 java 实现 websocket的五种方式_java_萧曵 丶-GitCode 开源社区...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...


