动态规划:分割等和子集
参考资料:代码随想录
题目链接:. - 力扣(LeetCode)
这道题是01背包问题的抽象,这道题的难点在于怎么绕明白遍历顺序是从后往前。
题目中给的nums数组,以nums=[1,5,11,5]为例,可以分析为有4个物品,每个物品的重量为weight=[1,5,11,5],每个物品的价值为value=[1,5,11,5]
最大容量为:(1+5+11+5)/2
1.确定dp数组含义
重量从0到maxWeight,分别能装的最大价值
2.初始化dp数组
全部初始化为0
3.确定遍历顺序
只能选取一次,从后向前
4.确定递推公式
class Solution {public boolean canPartition(int[] nums) {//求最大重量int sum = 0;for(int num:nums){sum+=num;}if(sum%2 != 0) return false;int maxWeight = sum/2;//1.确定dp数组含义int[] dp = new int[maxWeight+1];//2.初始化dp数组//3.确定遍历顺序for(int i = 0;i < nums.length;i++){for(int j = maxWeight;j >=nums[i] ;j--){//4.确定递推公式if(j >= nums[i]){dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);}}}return dp[maxWeight] == maxWeight;}
}相关文章:

动态规划:分割等和子集
参考资料:代码随想录 题目链接:. - 力扣(LeetCode) 这道题是01背包问题的抽象,这道题的难点在于怎么绕明白遍历顺序是从后往前。 题目中给的nums数组,以nums[1,5,11,5]为例,可以分析为有4个物…...

踩坑——纪实
开发踩坑纪实 1 npm安装1.1 查看当前的npm镜像设置1.2 清空缓存1.3 修改镜像1.4 查看修改结果1.5 重新安装vue 2 VScode——NPM脚本窗口找不到3 springboot项目中updateById()失效4 前端跨域4.1 后端加个配置类4.2 CrossOrigin注解 5 路由出口6 springdoc openapi3 swagger3文件…...
)
java实现websocket的五种方式(mark下)
java实现websocket的五种方式 java 实现 websocket的五种方式_java_萧曵 丶-GitCode 开源社区...

网络安全技术心得体会
网络与信息安全技术心得体会 通过对网络安全这门课程的学习,我进一步了解了网络安全技术的相关知识。大致来说,所谓网络安全指的是对网络系统中各类软硬件和数据信息等提供保护屏障,确保数据信息不受到恶意侵入、窃取等破坏,保证…...

光耦合器的特性和应用概述
光耦合器又称光电耦合器,是现代电子学中必不可少的元件,确保隔离电路之间安全有效的信号传输。本文探讨了光耦合器的特性及其多样化应用,强调了它们在各种电子系统中的关键作用。 什么是光耦合器? 光耦合器是一种设计用于利用光传…...

工作干到抑郁了,要不要辞职?
在知乎上看到以为网友提问:工作干到抑郁,该不该辞职? 今天和大家聊聊这个话题,如果你也有类似的情况,希望这篇文章能帮到你。 熟悉瑶琴的朋友,都知道瑶琴在去年有一次裸辞的经历。离职前,严重的…...

Vs Code插件位置:
Vs Code插件位置: C:\Users\dell.vscode\extensions...

521源码-免费源码-子比主题最新版7.6绕授权破解完整教程
首先,zibll主题授权是向api.zibll.com发送请求,api.zibll.com就验证这个请求,如果参数(比如header)正确那么授权成功,然而众所周知,服务器可以修改本地host文件,来实现某些特定功能,把host文件加…...

前端基础入门三大核心之HTML篇:Webpack、Vite、Grunt、Gulp的场景与实战运用
前端基础入门三大核心之HTML篇:Webpack、Vite、Grunt、Gulp的场景与实战运用 一、Webpack:模块打包与优化的集大成者基本概念与作用应用场景实战例 二、Vite:快速开发的现代化构建利器基本概念应用场景实战例 三、Gulp:任务自动化…...
java面试框架篇(Spring常见问题、SpringBoot、SpringMVC、mybatis经典问题、SpringCloud组件)
文章目录 面试专题-java框架篇1. spring常见问题1.1. spring是什么?1.2. 谈谈你对AOP的理解1.3. 谈谈你对IOC的理解1.4. Spring Boot、 Spring MVC和Spring有什么区别1.5. spring bean 生命周期1.6. spring事务传播机制有哪些?1.7. 循环依赖1.8. spring框架中使用了哪些设计模…...

HarmonyOS之ArkUI布局设计常见细节
这里写目录标题 1. Button设置带有渐变色的背景图片无效1.1 问题分析1.2 成功案例 2. 路由跳转失败2.1 问题分析 1. Button设置带有渐变色的背景图片无效 1.1 问题分析 说明:设置颜色渐变需先设置backgroundColor为透明色。 Button($r(app.string.login), { type…...

元宇宙虚拟线上会议,可应用于哪些行业和领域?
随着科技的飞速进步和互联网的广泛普及,线上元宇宙会议以其独特的魅力和优势,逐渐崭露头角,积木易搭旗下的元宇宙数字营销平台——视创云展,为线上元宇宙会议提供了全方位的服务,不仅涵盖了场景搭建、数字人互动、在线…...

【C++刷题】优选算法——递归第二辑
全排列 vector<vector<int>> vv; void dfs(vector<int>& nums, vector<int>& v, vector<bool>& check) {if(v.size() nums.size()){vv.push_back(v);return;}for(int i 0; i < nums.size(); i){if(check[i] false){v.push_ba…...
【GO基础】1. Go语言环境搭建
Go语言环境搭建 Go的三种安装方式Go标准包安装Windows 安装验证是否安装成功 4.Go的第一个程序 Hello World.go Go的三种安装方式 Go有多种安装方式,可以选择自己适合的。这里介绍三种最常见的安装方式: Go源码安装:这是一种标准的软件安装…...
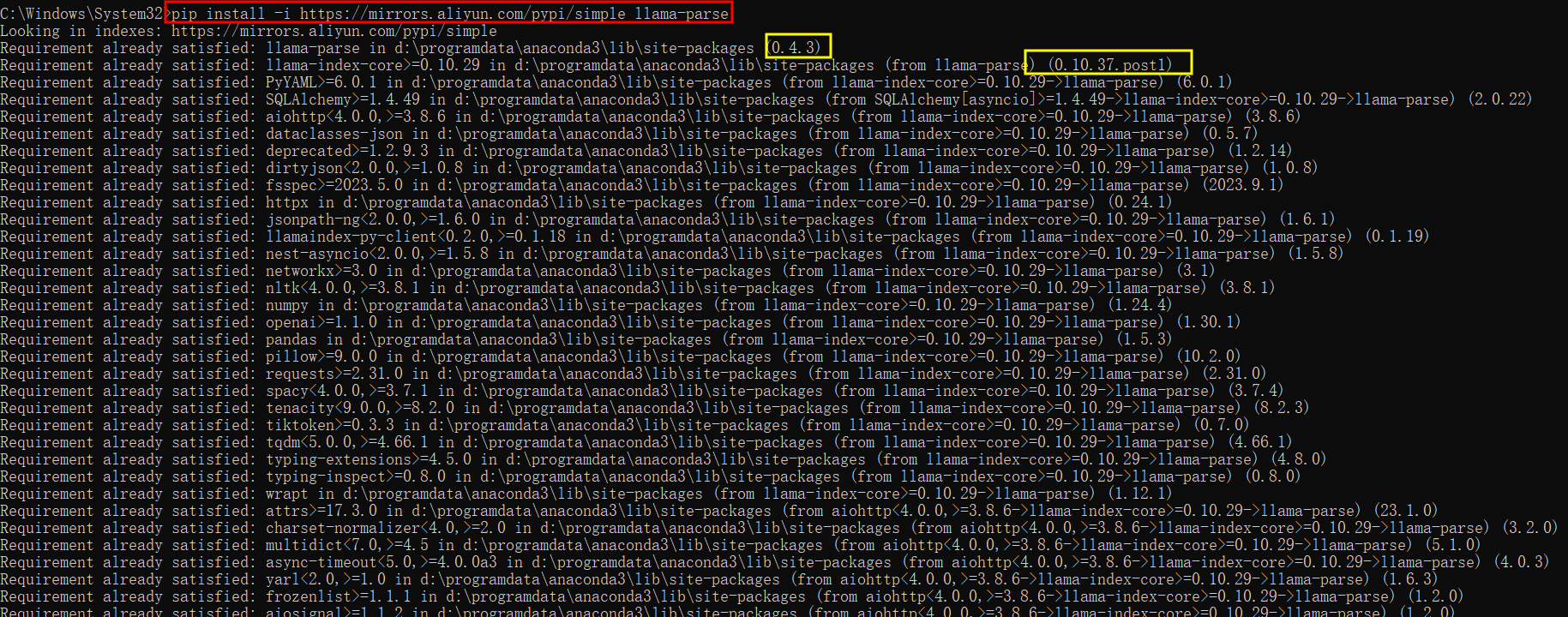
Py之llama-parse:llama-parse(高效解析和表示文件)的简介、安装和使用方法、案例应用之详细攻略
Py之llama-parse:llama-parse(高效解析和表示文件)的简介、安装和使用方法、案例应用之详细攻略 目录 llama-parse的简介 llama-parse的安装和使用方法 1、安装 2、使用方法 第一步,获取API 密钥 第二步,安装LlamaIndex、LlamaParse L…...

Python库之Scrapy的高级用法深度解析
Python库之Scrapy的高级用法深度解析 引言 Scrapy是一个强大的Web爬虫框架,它提供了丰富的功能和灵活的扩展性,使得在Python中编写爬虫变得简单而高效。本文将深入探讨Scrapy的高级用法,帮助读者充分利用Scrapy的强大功能。 目录 引言Scr…...
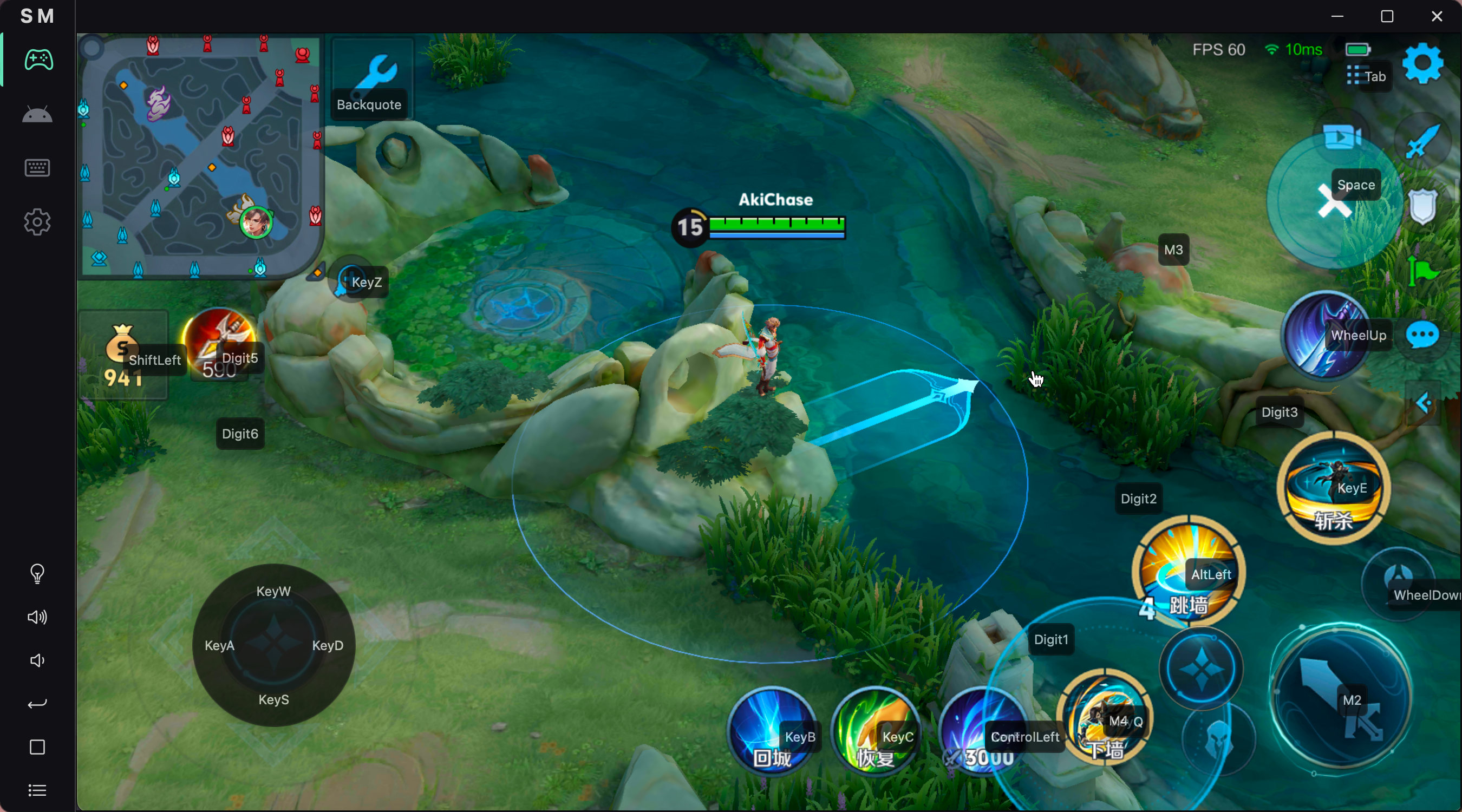
Rust Tarui 中的 Scrcpy 客户端,旨在提供控制安卓设备的鼠标和按键映射,类似于游戏模拟器。
Scrcpy-mask 为了实现电脑控制安卓设备,本人使用 Tarui Vue 3 Rust 开发了一款跨平台桌面客户端。该客户端能够提供可视化的鼠标和键盘按键映射配置。通过按键映射实现了实现类似安卓模拟器的多点触控操作,具有毫秒级响应速度。该工具可广泛用于电脑控…...

【shell】脚本练习题
案例: 1. for ping测试指网段的主机 网段由用户输入,例如用户输入192.168.2 ,则ping 192.168.2.10 --- 192.168.2.20 UP: /tmp/host_up.txt Down: /tmp/host_down.txt 2. 使用case实现成绩优良差的判断 1. for ping测试指…...

微信小程序uniapp+django洗脚按摩足浴城消费系统springboot
原生wxml开发对Node、预编译器、webpack支持不好,影响开发效率和工程构建。所以都会用uniapp框架开发 前后端分离,后端给接口和API文档,注重前端,接近原生系统 使用Navicat或者其它工具,在mysql中创建对应名称的数据库࿰…...

超链接的魅力:HTML中的 `<a>` 标签全方位探索!
🌐超链接的魅力:HTML中的 标签全方位探索! 🏞️基础营地:认识 <a> 标签🛠️基本语法📚属性扩展 🚀实战演练:超链接的多样玩法🌈内链与外链Ὄ…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
