元宇宙虚拟线上会议,可应用于哪些行业和领域?
随着科技的飞速进步和互联网的广泛普及,线上元宇宙会议以其独特的魅力和优势,逐渐崭露头角,积木易搭旗下的元宇宙数字营销平台——视创云展,为线上元宇宙会议提供了全方位的服务,不仅涵盖了场景搭建、数字人互动、在线投屏等核心功能,还实现了线上同步直播,打破了传统会议的时空限制,主要有以下应用场景:
01、企业会议
元宇宙会议打破了地域的限制,使企业能够轻松举办全球范围内的虚拟会议,参会者即便身处遥远的地方也能远程参与会议,体验到仿佛置身真实会议场景的沉浸式氛围。

02、学术会议
元宇宙会议为学术界构建了一个线上交流平台,使得学者和研究人员能够远程参与学术会议,共同分享最新的研究成果和学术见解,与其他参会者进行实时互动和深入讨论。

03、行业展会
通过元宇宙技术,行业展会得以突破时空限制,构建出一个虚拟的展览平台。参展商可以在这个平台上展示最新产品、发布创新技术,并与全球范围内的潜在客户和合作伙伴进行实时互动和交流。观众则能够通过虚拟现实技术,身临其境地参观各个展馆,深入了解行业动态和产品信息。

04、文化娱乐
通过元宇宙技术,人们可以跨越地域限制,共同参与各种线上文化活动,如音乐会、演唱会、艺术展览等。观众可以身临其境地感受现场氛围,与艺术家和表演者进行实时互动。

总之,积木易搭旗下视创云展平台凭借强大的技术实力和创新理念,为线上元宇宙论坛提供了卓越的技术支持和服务,为参会者带来了一场精彩绝伦的线上体验。
相关文章:

元宇宙虚拟线上会议,可应用于哪些行业和领域?
随着科技的飞速进步和互联网的广泛普及,线上元宇宙会议以其独特的魅力和优势,逐渐崭露头角,积木易搭旗下的元宇宙数字营销平台——视创云展,为线上元宇宙会议提供了全方位的服务,不仅涵盖了场景搭建、数字人互动、在线…...

【C++刷题】优选算法——递归第二辑
全排列 vector<vector<int>> vv; void dfs(vector<int>& nums, vector<int>& v, vector<bool>& check) {if(v.size() nums.size()){vv.push_back(v);return;}for(int i 0; i < nums.size(); i){if(check[i] false){v.push_ba…...
【GO基础】1. Go语言环境搭建
Go语言环境搭建 Go的三种安装方式Go标准包安装Windows 安装验证是否安装成功 4.Go的第一个程序 Hello World.go Go的三种安装方式 Go有多种安装方式,可以选择自己适合的。这里介绍三种最常见的安装方式: Go源码安装:这是一种标准的软件安装…...
Py之llama-parse:llama-parse(高效解析和表示文件)的简介、安装和使用方法、案例应用之详细攻略
Py之llama-parse:llama-parse(高效解析和表示文件)的简介、安装和使用方法、案例应用之详细攻略 目录 llama-parse的简介 llama-parse的安装和使用方法 1、安装 2、使用方法 第一步,获取API 密钥 第二步,安装LlamaIndex、LlamaParse L…...

Python库之Scrapy的高级用法深度解析
Python库之Scrapy的高级用法深度解析 引言 Scrapy是一个强大的Web爬虫框架,它提供了丰富的功能和灵活的扩展性,使得在Python中编写爬虫变得简单而高效。本文将深入探讨Scrapy的高级用法,帮助读者充分利用Scrapy的强大功能。 目录 引言Scr…...
Rust Tarui 中的 Scrcpy 客户端,旨在提供控制安卓设备的鼠标和按键映射,类似于游戏模拟器。
Scrcpy-mask 为了实现电脑控制安卓设备,本人使用 Tarui Vue 3 Rust 开发了一款跨平台桌面客户端。该客户端能够提供可视化的鼠标和键盘按键映射配置。通过按键映射实现了实现类似安卓模拟器的多点触控操作,具有毫秒级响应速度。该工具可广泛用于电脑控…...

【shell】脚本练习题
案例: 1. for ping测试指网段的主机 网段由用户输入,例如用户输入192.168.2 ,则ping 192.168.2.10 --- 192.168.2.20 UP: /tmp/host_up.txt Down: /tmp/host_down.txt 2. 使用case实现成绩优良差的判断 1. for ping测试指…...

微信小程序uniapp+django洗脚按摩足浴城消费系统springboot
原生wxml开发对Node、预编译器、webpack支持不好,影响开发效率和工程构建。所以都会用uniapp框架开发 前后端分离,后端给接口和API文档,注重前端,接近原生系统 使用Navicat或者其它工具,在mysql中创建对应名称的数据库࿰…...

超链接的魅力:HTML中的 `<a>` 标签全方位探索!
🌐超链接的魅力:HTML中的 标签全方位探索! 🏞️基础营地:认识 <a> 标签🛠️基本语法📚属性扩展 🚀实战演练:超链接的多样玩法🌈内链与外链Ὄ…...

与优秀者同行,“复制经验”是成功的最快捷径
富在术数不在劳身,利在局势不在力耕。我们始终相信,与优秀者同行,“复制经验”才是走向成功的最快“捷径”! 酷雷曼合作商交流会 作为酷雷曼合作商帮扶体系里的重要一环,合作商交流会是总部专门为合作商们搭建的一个博采众长、相…...

MobaXterm使用私钥远程登陆linux
秘钥的形式使用MobaXterm 远程连接 linux 服务器 MobaXterm使用私钥远程登陆linux just填写远程主机 不指定用户 勾选使用私钥 选择私钥即可 1.使用秘钥连接 远程linux 服务器的好处 只需要第一次添加秘钥,并输入密码后,以后再连接就不需要再输入密码…...
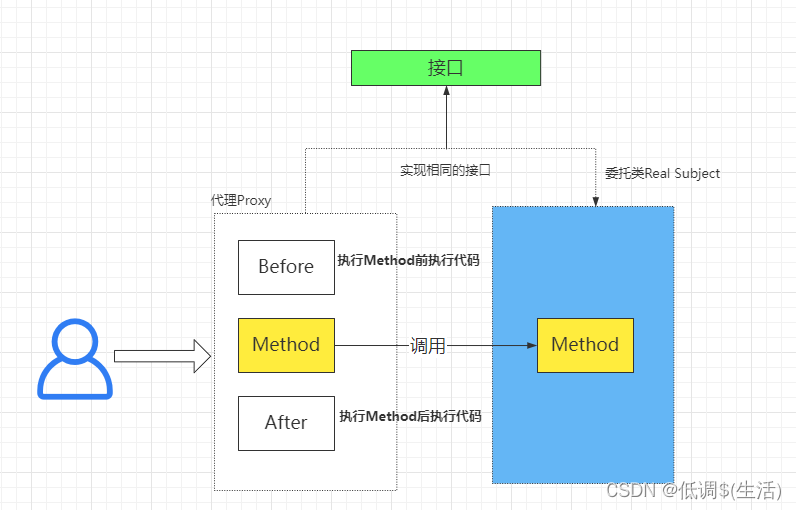
Java设计模式(23种设计模式 重点介绍一些常用的)
创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器模式、装饰器模式、代理模式、外观模式、桥接模式、组合模式、享元模式。行为型模式,共十一种:…...
JVM(5):虚拟机性能分析和故障解决工具概述
1 工具概述 作为一个java程序员,最基本的要求就是用java语言编写程序,并能够在jvm虚拟机上正常运行,但是在实际开发过程中,我们所有的程序由于各种各样的原因,并不是总能够正常运行,经常会发生故障或者程序…...
vue3插槽solt 使用
背景增加组件的复用性,个人体验组件化还是react 方便。 Vue插槽solt如何传递具名插槽的数据给子组件? 一、solt 原理 知其然知其所以然 Vue的插槽(slots)是一种分发内容的机制,允许你在组件模板中定义可插入的内容…...

正则项学习笔记
目录 1. L2 正则化 岭回归 1.1 L2 norm计算例子 2. L1 正则化 3. 弹性网正则化 4. Dropout 1. L2 正则化 岭回归 在 PyTorch 中,L2 正则化通常通过设置优化器的 weight_decay 参数实现。以下是一个简单的例子: 介绍博文: 正则化(1)&a…...

Django自定义模板标签与过滤器
title: Django自定义模板标签与过滤器 date: 2024/5/17 18:00:02 updated: 2024/5/17 18:00:02 categories: 后端开发 tags: Django模版自定义标签过滤器开发模板语法Python后端前端集成Web组件 Django模板系统基础 1. Django模板语言概述 Django模板语言(DTL&…...
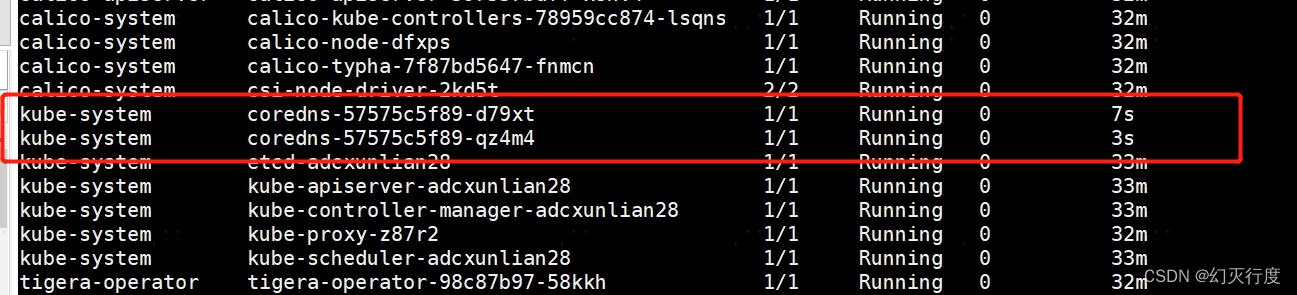
k8s集群安装后CoreDNS 启动报错plugin/forward: no nameservers found
安装k8s过程中遇到的问题: 基本信息 系统版本:ubuntu 22.04 故障现象: coredns 报错:plugin/forward: no nameservers found 故障排查: #检查coredns的配置,发现有一条转发到/etc/resolv.conf的配置…...
AI图片过拟合如何处理?答案就在其中!
遇到难题不要怕!厚德提问大佬答! 厚德提问大佬答8 你是否对AI绘画感兴趣却无从下手?是否有很多疑问却苦于没有大佬解答带你飞?从此刻开始这些问题都将迎刃而解!你感兴趣的话题,厚德云替你问,你解…...

0基础如何进入IT行业
目录 引言 一、了解IT行业 1.1 IT行业概述 1.2 IT行业的职业前景 二、选择适合的学习路径 2.1 自学 2.2 参加培训班 2.3 高等教育 三、学习基础技能 3.1 编程语言 3.2 数据结构与算法 3.3 计算机基础知识 四、实践与项目经验 4.1 开源项目 4.2 个人项目 4.3 实习…...
一键批量提取TXT文档前N行,高效处理海量文本数据,省时省力新方案!
大量的文本信息充斥着我们的工作与生活。无论是研究资料、项目文档还是市场报告,TXT文本文档都是我们获取和整理信息的重要来源。然而,面对成百上千个TXT文档,如何快速提取所需的关键信息,提高工作效率,成为了许多人头…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
