【MYSQL】分数排名
表: Scores
+-------------+---------+ | Column Name | Type | +-------------+---------+ | id | int | | score | decimal | +-------------+---------+ id 是该表的主键(有不同值的列)。 该表的每一行都包含了一场比赛的分数。Score 是一个有两位小数点的浮点值。
编写一个解决方案来查询分数的排名。排名按以下规则计算:
- 分数应按从高到低排列。
- 如果两个分数相等,那么两个分数的排名应该相同。
- 在排名相同的分数后,排名数应该是下一个连续的整数。换句话说,排名之间不应该有空缺的数字。
按 score 降序返回结果表。
查询结果格式如下所示。
示例 1:
输入: Scores 表: +----+-------+ | id | score | +----+-------+ | 1 | 3.50 | | 2 | 3.65 | | 3 | 4.00 | | 4 | 3.85 | | 5 | 4.00 | | 6 | 3.65 | +----+-------+ 输出: +-------+------+ | score | rank | +-------+------+ | 4.00 | 1 | | 4.00 | 1 | | 3.85 | 2 | | 3.65 | 3 | | 3.65 | 3 | | 3.50 | 4 | +-------+------+
MySQL
对于 SQL 用户,熟悉 窗口函数 在这里是有用的(对于大多数更高级的 SQL 问题也是如此):
窗口函数对一组查询行执行类似于聚合的操作。但是,聚合操作将查询行分组为一个单独的结果行,而窗口函数为每个查询行生成一个结果。
DENSE_RANK() 窗口函数恰好是我们在这个问题中需要的:
返回当前行在其分区中的排名,没有间隙。对等项被视为并列并获得相同的排名。此函数为对等组分配连续的排名;结果是大于一的组不产生不连续的排名号码。
看起来我们可以在这个问题中很好地使用 DENSE_RANK() 窗口函数。
SELECTS.score,DENSE_RANK() OVER (ORDER BYS.score DESC) AS 'rank'
FROMScores S;注意: MySQL 在 8.0 版本(2018 年 4 月 19 日)之前不支持窗口函数。一般来说,窗口函数直到 SQL:2003 才被引入 SQL,正如 MariaDB 的 窗口函数概述 文章中所述。
方法 2: 使用 COUNT(DISTINCT ...) 的相关子查询
简述
如果我们能够计算每个分数 S1.score 的不同分数 S2.score 的数量,而这些分数大于或等于此分数,那么这将有效地给我们提供 S1.score 的排名。然后我们可以按照 S1.score 对结果集进行排序,以符合问题的排名规则。
实现
可以使用 相关子查询 来完成上述的计数。
1.对于来自 Scores 表的每个分数,选择在 Scores 表中大于或等于此分数的不同分数的数量。
2.按照 score 对结果集进行排序。
SELECTS1.score,(SELECTCOUNT(DISTINCT S2.score)FROMScores S2WHERES2.score >= S1.score) AS 'rank'
FROMScores S1
ORDER BYS1.score DESC;
方法 3:使用 INNER JOIN 和 COUNT(DISTINCT...)
简述
这个方法的基本思想与 方法 2 的相同,但实现方式完全不同。
实现
1.将 Scores 表与自身连接,以便我们得到所有分数大于或等于此分数的所有行。
2.将查询行按 id 和 score 值进行分组。
3.计算唯一的分数的数量,它应该大于或等于连接条件中使用的分数(也就是排名)。
4.按 score 值对结果集进行排序。
MYSQL:
SELECTS.score,COUNT(DISTINCT T.score) AS 'rank'
FROMScores SINNER JOIN Scores T ON S.score <= T.score
GROUP BYS.id,S.score
ORDER BYS.score DESC;
上述解决方案是有效的,因为项目是如何分组的--COUNT() 聚合函数在分组上工作,从而为我们提供所需的结果。为了更清楚地看到上述查询的工作原理,我们可以检查以下查询的输出结果:
SELECTS.id AS S_ID,S.score AS S_Score,T.id AS T_ID,T.score AS T_Score
FROMScores SINNER JOIN Scores T ON S.score <= T.score
ORDER BYS.id,T.score;如果我们将这个查询应用于问题描述中给定的示例数据,那么我们将得到以下结果集:
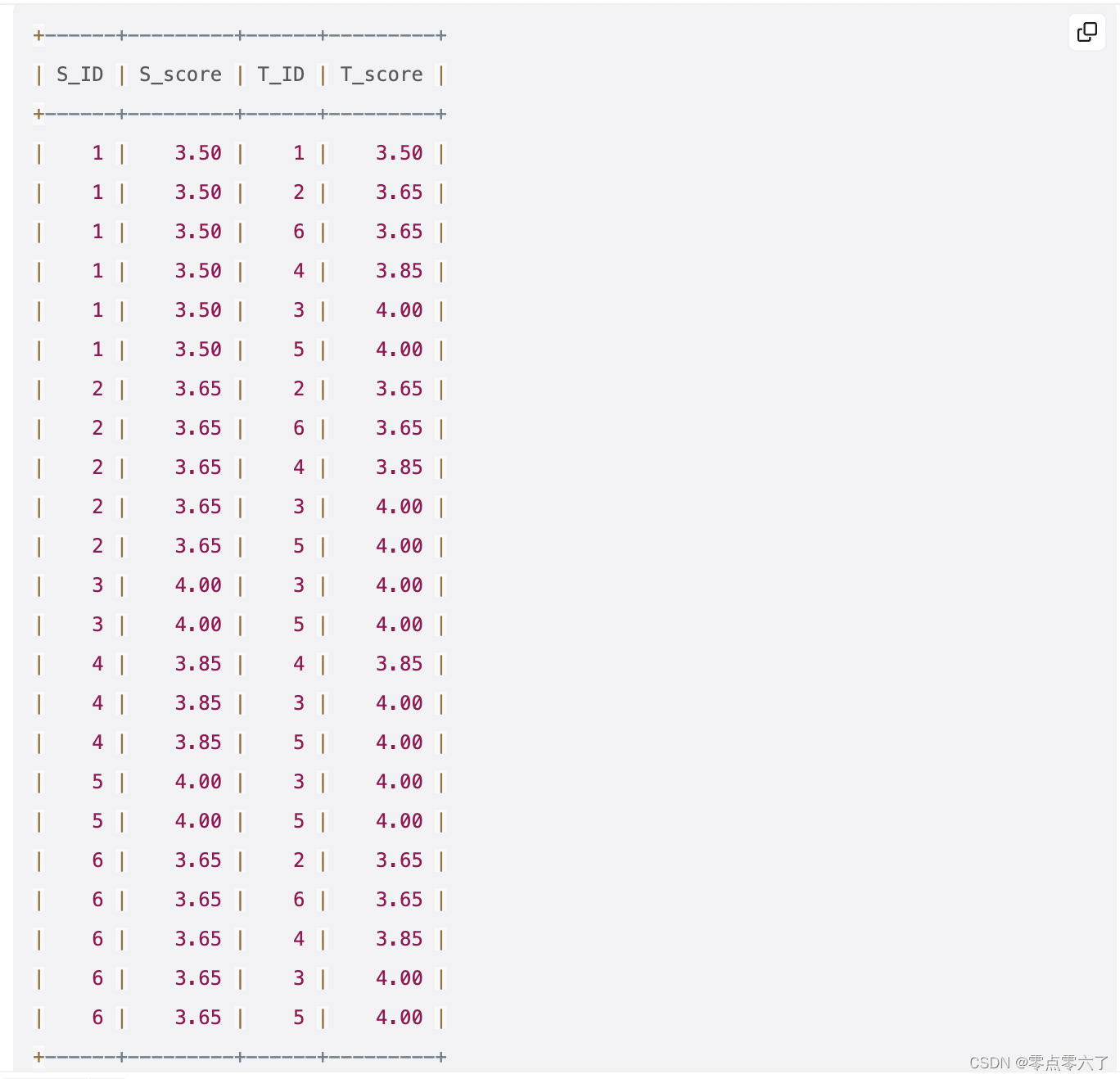
请注意,当我们在合适的分组上使用 COUNT(DISTINCT ...) 时,这为我们提供了所需的结果集

S_ID = 1;S_score = 3.50:有 4 个不同的 T_score 值(3.50、3.65、3.85 和 4.00)。
S_ID = 2;S_score = 3.65:有 3 个不同的 T_score 值(3.65、3.85 和 4.00)。
...
结论
出于各种原因,我们更喜欢 方法 1,特别是它的简单性、性能和上下文适用性。很少有问题会要求如此恰当地直接应用 DENSE_RANK()。但是,如 方法 1 结尾所述,窗口函数在 SQL 领域的到来相对较新,特别是对于它们在现代开发环境中的使用方式。
在面试环境中,方法 1 是最优的。但如果面试官要求不使用现代 SQL 工具(如窗口函数)来解决问题,使用 方法 2 或 方法 3 也是适当的策略。在这种情况下,方法 2 可能传达对 SQL 查询处理方式的更深入理解,而 方法 3 可能传达解决问题的创造性。无论哪种情况,都传达了一种积极和值得欢迎的特质。
相关文章:

【MYSQL】分数排名
表: Scores ---------------------- | Column Name | Type | ---------------------- | id | int | | score | decimal | ---------------------- id 是该表的主键(有不同值的列)。 该表的每一行都包含了一场比赛的分数。Score 是…...
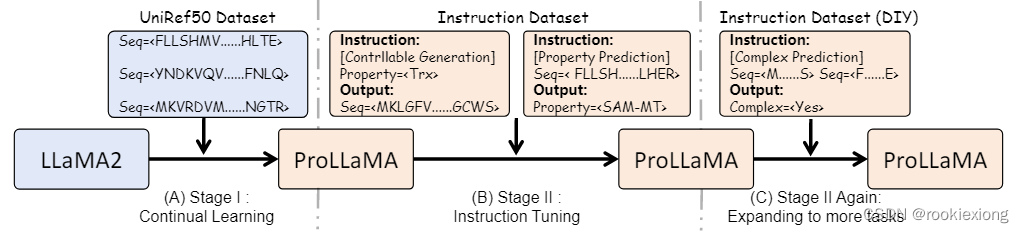
【论文笔记】| 蛋白质大模型ProLLaMA
【论文笔记】| 蛋白质大模型ProLLaMA ProLLaMA: A Protein Large Language Model for Multi-Task Protein Language Processing Peking University Theme: Domain Specific LLM Main work: 当前 ProLLM 的固有局限性:(i)缺乏自然…...
MySQL笔记第一天(从小白到入门)
文章目录 MySQL笔记SQL语言介绍数据库系统关系型数据库非关系型数据库SQL和数据库系统的关系数据库系统架构 MySQL的介绍概念MySQL的版本 MySQL的DDL操作-重点基本数据库操作基本表操作 MySQL的DML操作-重点insert-插入数据update-更新数据delete-删除数据 MySQL的约束-了解概述…...

初识Qt:从Hello world到对象树的深度解析
Qt中的对象树深度解析 Hello world1.图形化界面创建命令行式创建在栈上创建在堆上创建为什么传文本需要QString,std::string不行吗?那为什么要传入this指针?为什么new后不用显示调用delete函数呢,不会造成内存泄漏问题吗ÿ…...
多维数据库创建
多维数据库 小白的数据仓库学习笔记 2024/5/21 上午 文章目录 多维数据库Cube的作用:什么是多维数据库维的级别多维数据分析方法如何构建多维数据集?创建项目创建数据源创建数据源视图创建多维数据集维度表中缺失的值拖拽过去建立维度结构设计类型启动连…...

win11安装docker运行Open-Webui 界面化展示 ollama大模型
1.OpenWeb UI运行需要docker 环境下载docker Get Started | Docker 2.需要命令提示符docker -v 查询是否安装成功; 查询docker详情docker version 3.github拉取open-webUi镜像Package open-webui GitHub 复制命令运行在命令提示符; 等待下载完成 4.到…...
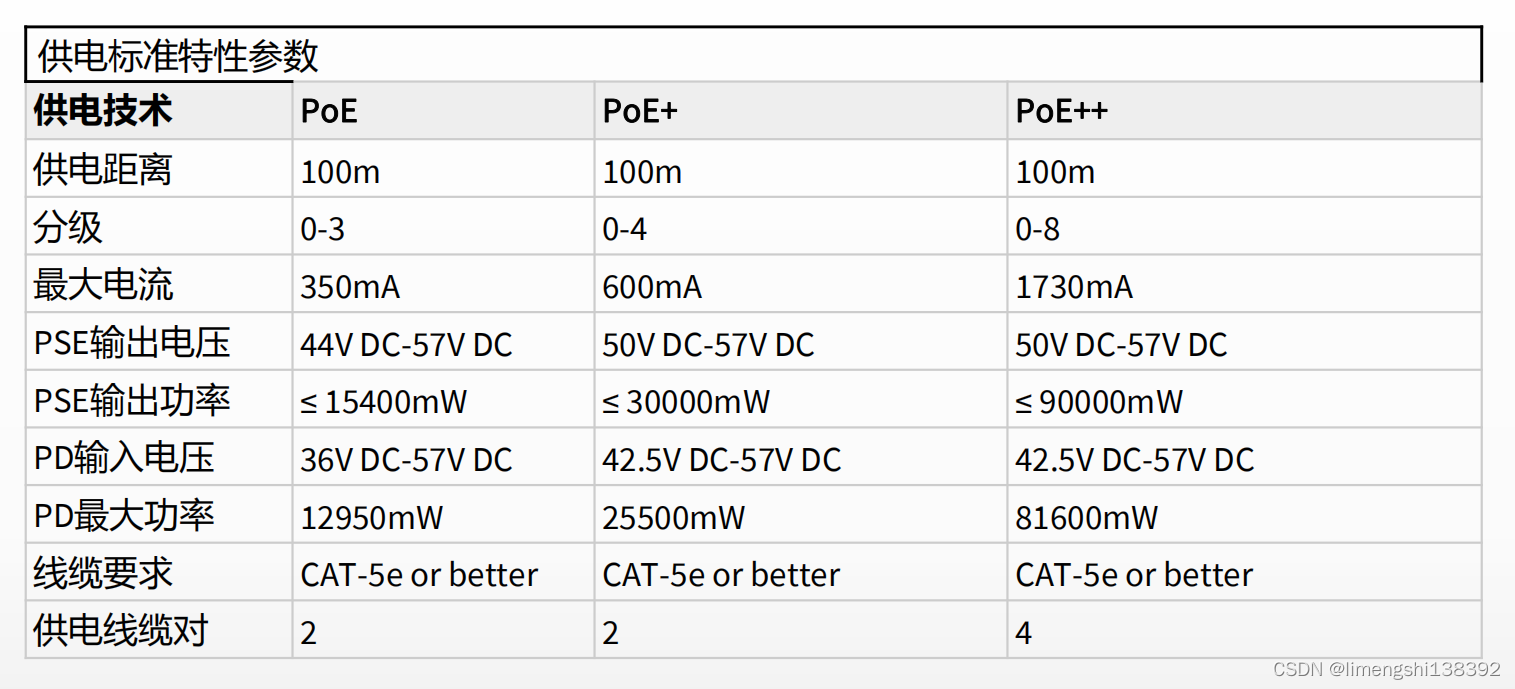
网络模型-PoE技术
一、PoE简介 以太网供电PoE(Powerover Ethernet)是指通过以太网网络进行供电,也被称为基于局域网的供电系统PoL(PoweroverLAN)或有源以太网(Active Ethernet)。 1、PoE的优势: 可靠: 电源集中供电,备份方便。连接简捷: 网络终端不需外接电源…...
网站策划是什么
网站策划是指在建立、设计和运营一个网站时所采取的系统性规划和组织活动。它涵盖了从确定网站的目标和目标受众到确定内容、功能、设计和营销策略等方面的各个方面。在今天互联网时代的背景下,网站已经成为企业、组织和个人展示自身形象、提供信息和服务、开展交流…...

MySQL基础学习: SET FOREIGN_KEY_CHECKS = 0
文章目录 一、介绍二、使用方法三、注意事项 一、介绍 在MySQL中,SET FOREIGN_KEY_CHECKS 0; 是一个特殊的命令,用于临时禁用外键约束检查。这在你执行一些涉及多个表并且可能违反外键约束的批量操作时非常有用。 为什么需要禁用外键约束检查…...
信号:MSK调制和GMSK调制
目录 一、MSK信号 1. MSK信号的第k个码元 2.MSK信号的频率间隔 3.MSK信号的相位连续性 3.1 相位路径 3.2初始相位ψk 4.MSK信号的产生 原理框图 5.MSK信号的频谱图 二、高斯最小频移键控(GMSK) 1.频率响应 2.GMSK调制产生方式 2.1 高斯滤波器法 2.2 正交调制器法…...

计算请假申请时长
请假申请时提供一个开始和结束时间,计算这段时间内的上班时间为多少个小时 /*** 计算请假时长,周日不计算* param startTimeStr* param endTimeStr* return*/public double computeWorkTimeLength(String startTimeStr, String endTimeStr){// 获取配置的…...

linux-配置服务器之间 ssh免密登录
前言 在管理多台Linux服务器时,为了方便操作和自动化任务,实现服务器之间的SSH免密登录是非常有必要的。SSH免密登录可以避免每次远程连接时输入密码,大大提高效率。本文将详细介绍SSH免密登录的原理和实现步骤。 一、原理解释 SSH免密登录的实现依赖于SSH密钥对,主要是利用…...
Java入门基础学习笔记47——ArrayList
什么是集合呢? 集合是一种容器,用来装数据的,类似数组。 有数组,为什么还要学习集合呢? 数组定义完成并启动后,长度就固定了。 而集合是大小可变,开发中用的最多的。 集合的特点:大…...

案例题(第二版)
案例题目 信息系统架构设计 基本概念 信息系统架构(ISA)是对某一特定内容里的信息进行统筹、规划、设计、安排等一系列的有机处理的活动。特点如下 架构是对系统的抽象,它通过描述元素、元素的外部可见属性及元素之间的关系来反映这种抽象…...
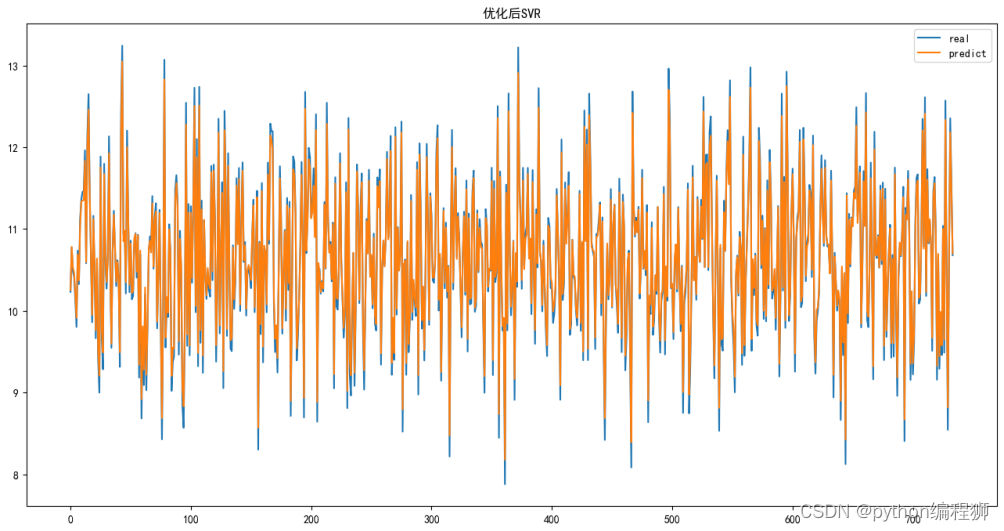
基于python向量机算法的数据分析与预测
3.1 数据来源信息 该数据集来源于Kaggle网站,数据集中包含了罗平菜籽油的销售数据,每行数据对应一条记录,记录了罗平菜籽油销售数据。其中,菜籽产量、菜籽价格和菜籽油价格是数值型数据,共2486条数据。 通过读取Exce…...
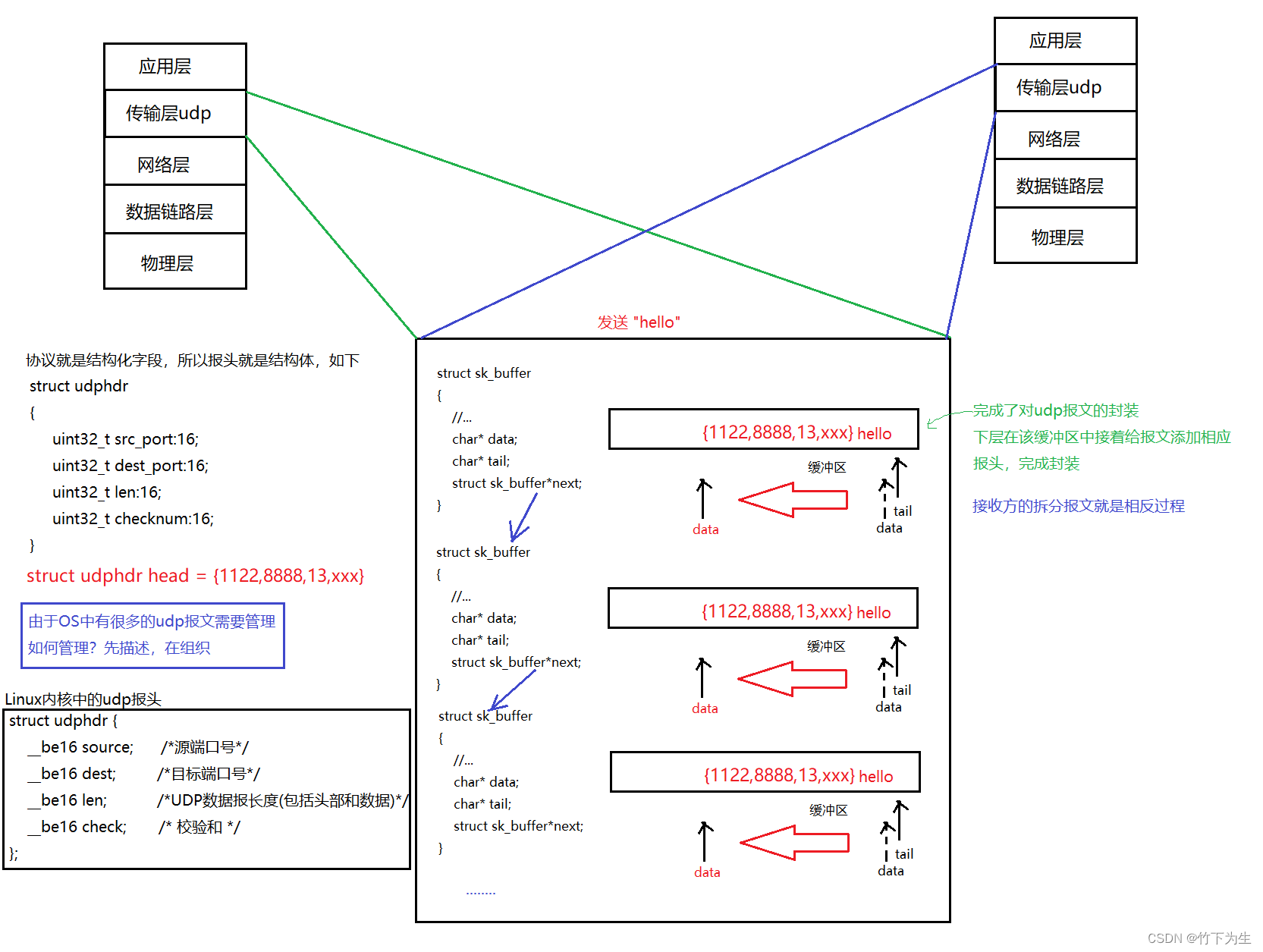
传输层 --- UDP
一、简述与回顾 传输层:负责数据能够从发送端传输接收端 在TCP/IP协议中,我们用"源IP","源端口号","目的IP","目的端口号",和"协议号"来表示一个通信。…...

图书管理系统(Java版本)
文章目录 前言要求1.设置对象1.1.图书1.2.书架2.管理员3.功能的实现 2.搭建框架2.1.登录(login)2.2.菜单2.3.操作方法的获取 3.操作方法的实现3.1.退出系统(ExitOperation)3.2.显示图书(ShowOperation)3.3.查阅图书(FindOperation)3.4.新增图书(AddOperation)3.5.借出图书(Borr…...

全同态加密生态项目盘点:FHE技术的崛起以及应用
撰文:Chris,Techub News 在当今数字化的时代,隐私保护已成为一个全球性的焦点话题,特别是在加密货币和区块链技术快速发展的背景下。虽然当前的隐私技术在保护数据安全方面多有欠缺,引发了广泛的关注和批评,…...

山脉数组的峰顶索引 ---- 二分查找
题目链接 题目: 分析: 我们很明显, 可以从峰值位置将数组分成两段, 具有"二段性", 所以可以用二分查找因为arr是山峰数组, 不存在相等的情况如果arr[mid] > arr[mid 1], 说明mid的位置可能是峰值, 移动right mid如果arr[mid] < arr[mid 1], 说明mid的位置…...

【简单介绍下7-Zip,什么是7-Zip?】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
