LeetCode 2644.找出可整除性得分最大的整数:暴力模拟(两层循环)
【LetMeFly】2644.找出可整除性得分最大的整数:暴力模拟(两层循环)
力扣题目链接:https://leetcode.cn/problems/find-the-maximum-divisibility-score/
给你两个下标从 0 开始的整数数组 nums 和 divisors 。
divisors[i] 的 可整除性得分 等于满足 nums[j] 能被 divisors[i] 整除的下标 j 的数量。
返回 可整除性得分 最大的整数 divisors[i] 。如果有多个整数具有最大得分,则返回数值最小的一个。
示例 1:
输入:nums = [4,7,9,3,9], divisors = [5,2,3] 输出:3 解释:divisors 中每个元素的可整除性得分为: divisors[0] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 5 整除。 divisors[1] 的可整除性得分为 1 ,因为 nums[0] 能被 2 整除。 divisors[2] 的可整除性得分为 3 ,因为 nums[2]、nums[3] 和 nums[4] 都能被 3 整除。 因此,返回 divisors[2] ,它的可整除性得分最大。
示例 2:
输入:nums = [20,14,21,10], divisors = [5,7,5] 输出:5 解释:divisors 中每个元素的可整除性得分为: divisors[0] 的可整除性得分为 2 ,因为 nums[0] 和 nums[3] 都能被 5 整除。 divisors[1] 的可整除性得分为 2 ,因为 nums[1] 和 nums[2] 都能被 7 整除。 divisors[2] 的可整除性得分为 2 ,因为 nums[0] 和 nums[3] 都能被5整除。 由于 divisors[0]、divisors[1] 和 divisors[2] 的可整除性得分都是最大的,因此,我们返回数值最小的一个,即 divisors[2] 。
示例 3:
输入:nums = [12], divisors = [10,16] 输出:10 解释:divisors 中每个元素的可整除性得分为: divisors[0] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 10 整除。 divisors[1] 的可整除性得分为 0 ,因为 nums 中没有任何数字能被 16 整除。 由于 divisors[0] 和 divisors[1] 的可整除性得分都是最大的,因此,我们返回数值最小的一个,即 divisors[0] 。
提示:
1 <= nums.length, divisors.length <= 10001 <= nums[i], divisors[i] <= 109
解题方法:两层循环枚举
外层循环遍历每一个“被除数”,对于某个被除数 d d d,记录其“可整除性得分”。
- 如果这个得分大于历史最大得分,更新最大得分并将其暂时视为答案;
- 如果这个得分等于历史最大得分,将它和“临时答案”中最小的那个暂时视为答案。
最终的“临时答案”即为最终答案。
- 时间复杂度 O ( l e n ( n u m s ) × l e n ( d i v i s o r s ) ) O(len(nums)\times len(divisors)) O(len(nums)×len(divisors))
- 空间复杂度 O ( N log N ) O(N\log N) O(NlogN)
本题似乎没有更小的时空复杂度的算法,能做的似乎最多是一些剪枝。
AC代码
C++
class Solution {
public:int maxDivScore(vector<int>& nums, vector<int>& divisors) {int M = -1, ans = 0;for (int d : divisors) {int thisCnt = 0;for (int n : nums) {if (n % d == 0) {thisCnt++;}}if (thisCnt > M) {M = thisCnt;ans = d;}else if (thisCnt == M) {M = thisCnt;ans = min(ans, d);}}return ans;}
};
Python
from typing import Listclass Solution:def maxDivScore(self, nums: List[int], divisors: List[int]) -> int:M, ans = -1, 0for d in divisors:thisCnt = 0for n in nums:thisCnt += n % d == 0if thisCnt > M:M = thisCntans = delif thisCnt == M:ans = min(ans, d)return ans
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/139026732
相关文章:
)
LeetCode 2644.找出可整除性得分最大的整数:暴力模拟(两层循环)
【LetMeFly】2644.找出可整除性得分最大的整数:暴力模拟(两层循环) 力扣题目链接:https://leetcode.cn/problems/find-the-maximum-divisibility-score/ 给你两个下标从 0 开始的整数数组 nums 和 divisors 。 divisors[i] 的 …...

Python列表,元组,集合,字典详解一篇搞懂
目录 介绍 列表(List) 集合(Set) 字典(Dict) 元组(Tuple) 列表 列表定义 编辑 列表切片 列表常用方法 append extend 编辑 insert 编辑 remove pop 编辑 clear 编辑 列表修改元素 sort 升序 倒序 reverse count 编辑 index 浅拷贝和深拷贝 …...
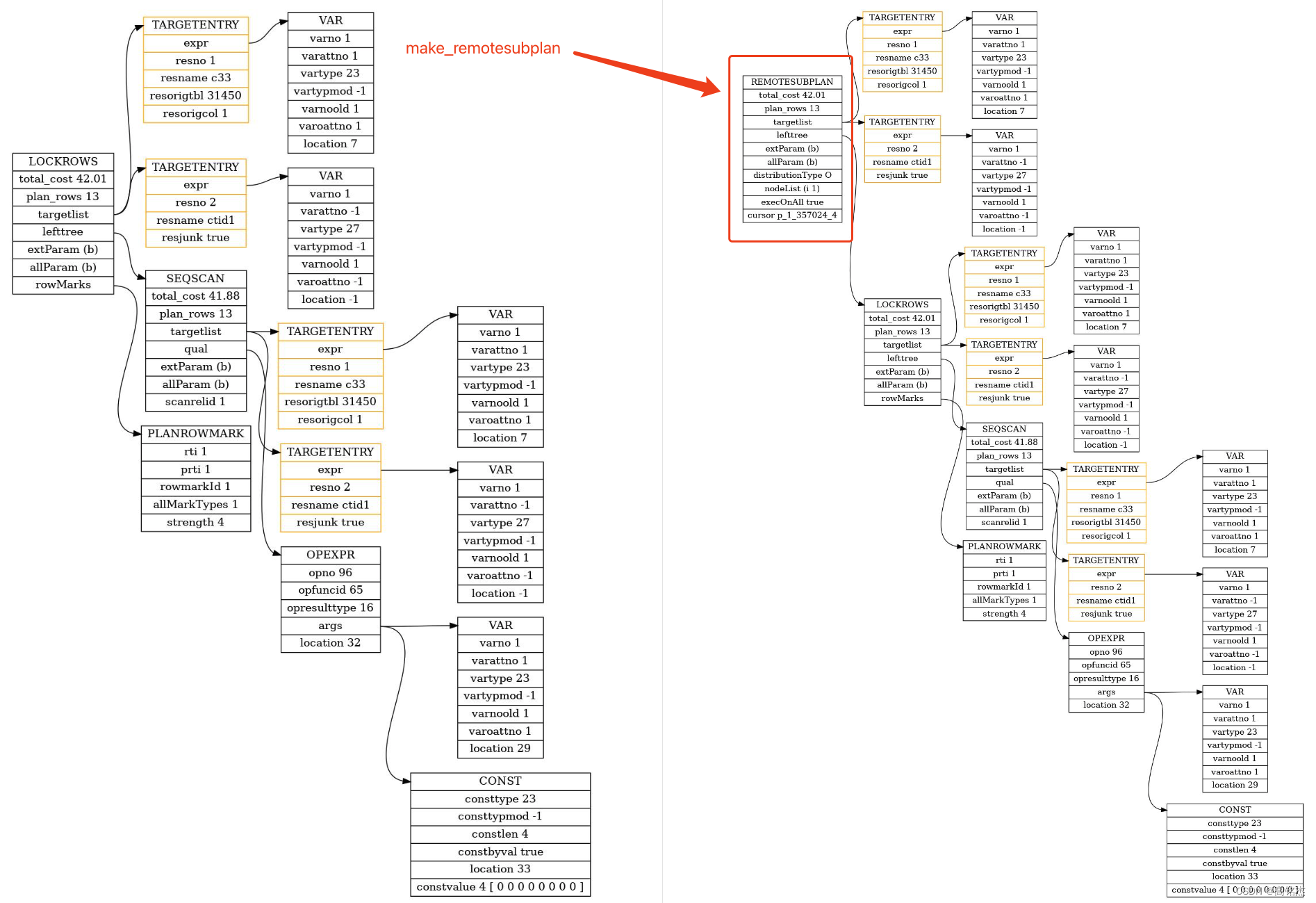
Postgresql源码(132)分布式行锁的原理分析
相关 《Postgresql源码(131)行锁的原理分析》 1 分布式行锁 PG中的行锁在上一片中做了分析《Postgresql源码(131)行锁的原理分析》,本篇对分布式PG(PGXL)中的行锁做一些分析。(版本…...

前端 防抖和节流
在前端开发中,防抖(Debounce)和节流(Throttle)是两种常用的性能优化技术,尤其在处理频繁触发的事件时显得尤为重要。无论是在用户输入、窗口调整大小,还是滚动事件中,这两种技术都可…...
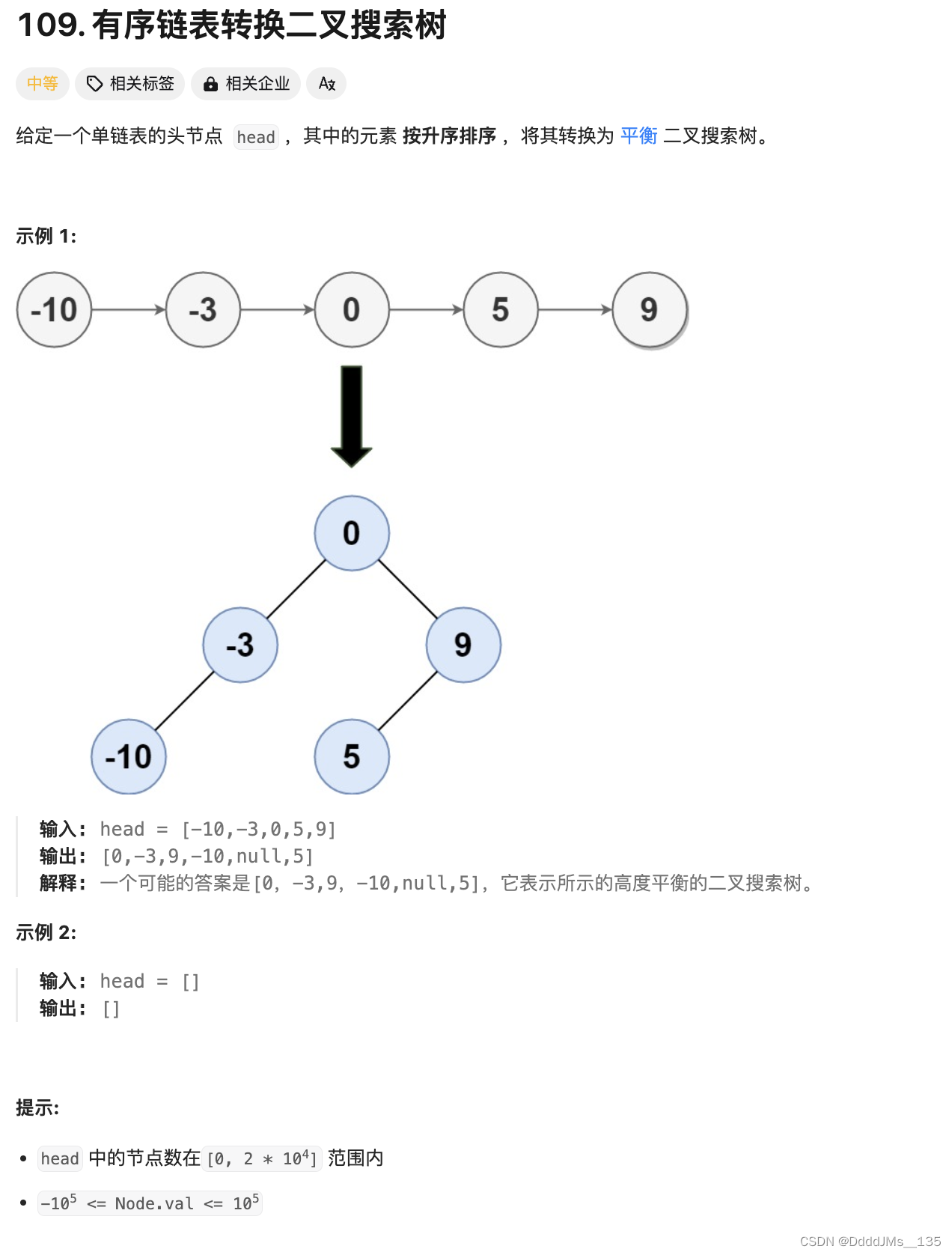
C语言 | Leetcode C语言题解之第109题有序链表转换二叉搜索树
题目: 题解: int getLength(struct ListNode* head) {int ret 0;while (head ! NULL) {ret, head head->next;}return ret; }struct TreeNode* buildTree(struct ListNode** head, int left, int right) {if (left > right) {return NULL;}int …...

【DevOps】Linux 下安装配置 Apache 服务器:打造你的专属 Web 平台
目录 一、准备工作 二、安装 Apache 三、启动和管理 Apache 四、验证安装 五、配置 Apache 5.1 修改网站根目录 5.2 配置虚拟主机 5.2.1 创建虚拟主机配置文件 5.2.2 创建网站目录 5.2.3 启用虚拟主机 5.2.4 重启 Apache 5.3 配置 HTTPS 5.3.1 安装 SSL 证书 5.3…...

23种设计模式之一————外观模式详细介绍与讲解
外观模式详细讲解 一、概念二、 外观模式结构核心思想及解释模式的UML类图模式角色应用场景模式优点模式缺点 三、实例演示图示代码展示运行结果 一、概念 外观模式(Facade Pattern)是一种结构型设计模式,它提供了一个统一的接口,…...
等级考试试卷(四级))
202109青少年软件编程(Python)等级考试试卷(四级)
第 1 题 【单选题】 执行如下 Python 代码后, 结果是?( ) def inverse(s,n=0): while s:n = n * 10 + s % 10s = s // 10return nprint...
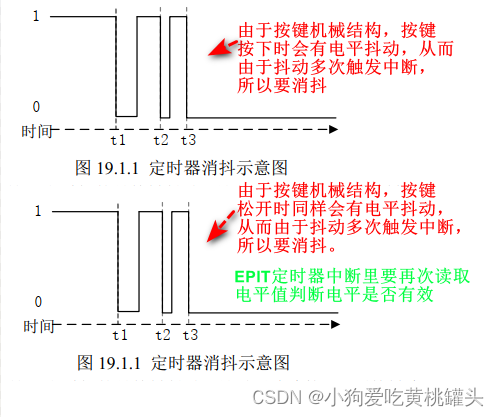
正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-17讲 定时器按键消抖
前言: 本文是根据哔哩哔哩网站上“正点原子[第二期]Linux之ARM(MX6U)裸机篇”视频的学习笔记,在这里会记录下正点原子 I.MX6ULL 开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了正点原子教学视频和链接中的内容。…...
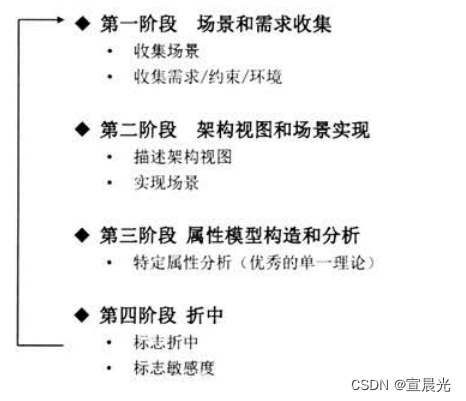
【系统架构师】-论文考点整理
1、软件架构风格 1.1、概述 1、软件架构为软件系统提供了一个结构、行为和属性的高级抽象。 2、软件架构风格是特定应用领域的惯用模式,架构定义一个词汇表和一组约束。 1.2、作用 1、软件架构是项目干系人进行交流的手段。 2、软件架构是可传递和可复用的模型&…...

Android Activity 设计详解
文章目录 Android Activity 设计说明1. Activity 的生命周期2. Activity 的启动模式3. Activity 的通信4. Activity 的布局和视图管理5. Activity 的配置变化处理6. Activity 的保存和恢复状态7. Activity 的任务和返回栈 总结 Android Activity 设计说明 在 Android 中&#…...

国家开放大学,javaScript程序设计-形考任务-实训五:设计登录和注册页|实训六:设计简单的购物车
实训五:设计登录和注册页 1. 题目 设计登录和注册页。 2. 目的 (1)掌握表单域的引用方法。 (2)掌握常用控件的基本方法。 (3)掌握事件的处理方法。 (4)理解Cookie…...
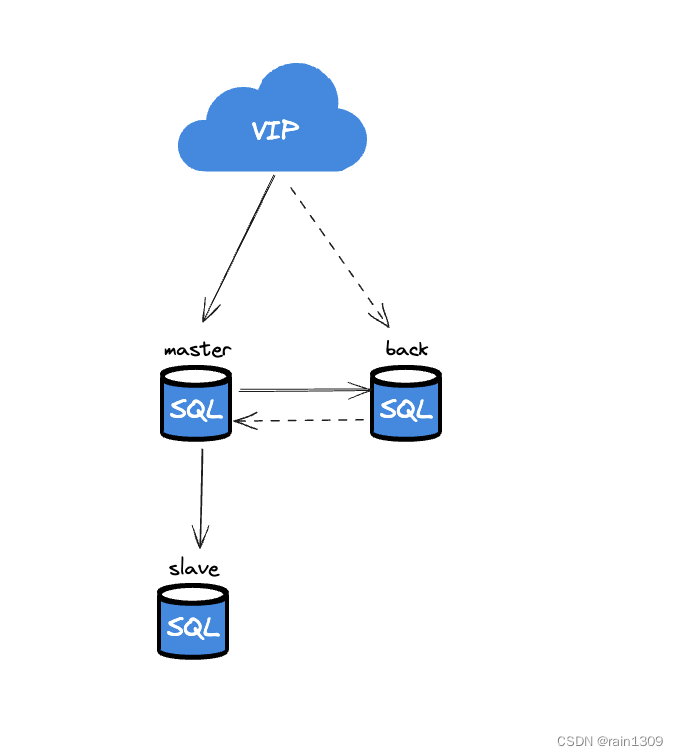
微服务可用性之隔离
摘要 本文主要微服务场景下服务的可用性保障之隔离。隔离又分为几种情况,动静隔离、读写隔离、热点隔离、资源隔离等场景。 为什么要隔离 本质上是对资源进行分割确保在出现故障的时候服务只是部分不可用,不至于系统陷入整体性瘫痪,…...

设计模式——概述
1.设计模式定义 设计模式是软件设计中常见问题的典型解决方案,可用于解决代码中反复出现的设计问题。设计模式的出现可以让我们站在前人的肩膀上,通过一些成熟的设计方案来指导新项目的开发和设计,以便于我们开发出具有更好的灵活性和可扩展性&#…...

#P0564. 数组元素查找升级版
问题描述 给你 n 个数,再给你一个数 k,查找 k 在这 n 个数中第一次出现的位置(从 0 开始计数),不存在输出 No。 输入 多组测试数据,对于每组测试数据: 第一行输入一个整数 n (1 ≤ n ≤ 100…...
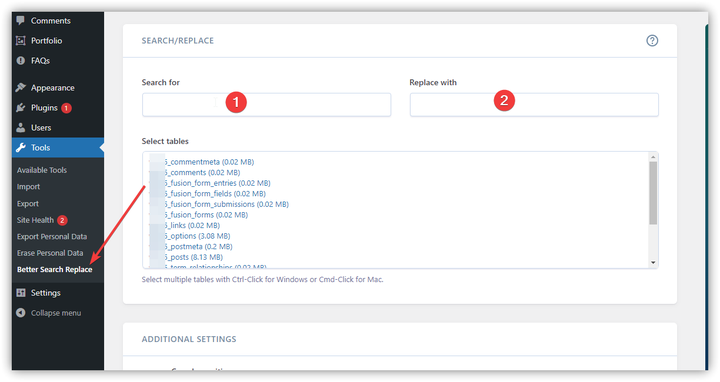
如何修改WordPress网站的域名
我的网站用的是Hostease的虚拟主机,但是域名是之前在其他平台买的,而且已经快到期了,因为主机和域名在不同的平台上,管理不太方便,所以我又在Hostease重新注册了一个域名,然后把网站换成了新的域名…...

python爬虫[简易版]
python爬数据[简易版] 对于每个网站的爬的原理基本是一样的,但是具体的代码写法的区别就在于爬的数据中解析出想要的数据格式: 以爬取有道词典中的图片为例: 第一步:打开网站,分析图片的数据源来自哪里, https://dict-subsidiary.youdao.com/home/content?invalid&pre…...

128天的创意之旅:从初心到成就,我的博客创作纪念日回顾
文章目录 🚀机缘:初心的种子——回望创作之旅的启航🌈收获:成长的果实——128天创作之旅的宝贵馈赠❤️日常:创作与生活的交织👊成就:代码的艺术🚲憧憬:未来的蓝图 &…...
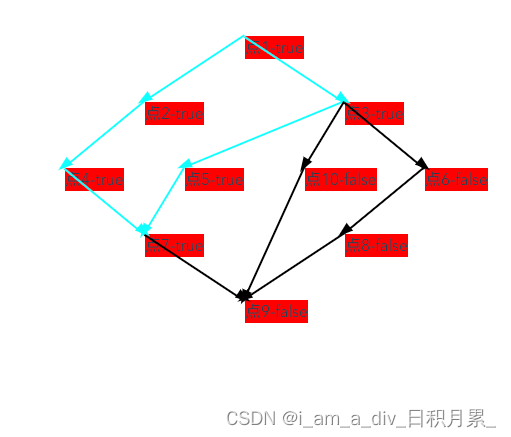
前端绘制流程节点数据
根据数据结构和节点的层级、子节点id,前端自己绘制节点位置和关联关系、指向、已完成节点等 <template><div><div>通过后端节点和层级,绘制出节点以及关联关系等</div><div class"container" ref"container&…...

2024年顶级算法-黑翅鸢优化算法(BKA)-详细原理(附matlab代码)
黑翅鸢是一种上半身蓝灰色,下半身白色的小型鸟类。它们的显著特征包括迁徙和捕食行为。它们以小型哺乳动物、爬行动物、鸟类和昆虫为食,具有很强的悬停能力,能够取得非凡的狩猎成功。受其狩猎技能和迁徙习惯的启发,该算法作者建立…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
