leetCode-hot100-数组专题之双指针
数组双指针专题
- 1.同向双指针
- 1.1例题
- 26.删除有序数组中的重复项
- 27.移除元素
- 80.删除有序数组中的重复项 Ⅱ
- 2.相向双指针
- 2.1例题
- 11.盛最多水的容器
- 42.接雨水
- 581.最短无序连续子数组
双指针在算法题中很常见,下面总结双指针在数组中的一些应用,主要分为两类:
1.同向双指针
题目中有原地、不适用额外空间等关键词,一般解决方法是定义两个快慢指针:
快指针:用来遍历数组,并进行一些规则匹配
慢指针:用来表示结果数组,即当前符合条件的数组
最后一般是返回慢指针的下标,需要注意的是有时候不能只返回慢指针的下标,可能需要+1,需要根据实际情况分析。
1.1例题
26.删除有序数组中的重复项
思路:
本题设置一个辅助下标指针idx指向数组的第一个元素,然后往后遍历数组,如果遇到了相同的元素就跳过,遇到不同的元素则加入到辅助下标的后一个元素,依次类推,直到遍历数组结束,最后返回idx+1即为所求的长度。详细的视频讲解点击视频讲解-删除有序数组中的重复项。
时间复杂度:
时间复杂度为O(n),只进行了一次数组的遍历。
代码实现:
class Solution {public int removeDuplicates(int[] nums) {if(nums.length < 2) return nums.length;int idx = 0;for(int i = 1;i < nums.length;i++){if(nums[i] != nums[idx]){idx = idx + 1;nums[idx] = nums[i];}}return idx + 1;}
}
27.移除元素
思路:
本题的思路和第26题一样,需要一个辅助下标idx,遍历整个数组,当遇到数组元素不等于val时,则将其加入到删除后的数组中,同时辅助下标后移,遍历结束后返回辅助下标idx的值即可,详细的视频讲解点击视频讲解-移除元素。
时间复杂度:
时间复杂度为O(n),n为数组的长度。
代码实现:
class Solution {public int removeElement(int[] nums, int val) {int idx = 0;for(int i = 0;i < nums.length;i++){if(nums[i] != val){nums[idx] = nums[i];idx = idx + 1;}}return idx;}
}
80.删除有序数组中的重复项 Ⅱ
思路:
本题采用双指针来求解,解法和26.删除有序数组中的重复项类似,但是由于本题中每个元素可以出现两次,所以将idx设置为1,设置前两个位置为结果数组,第二个指针从索引为2开始,比较当前元素和结果数组中的倒数第二个元素的值是否相等(即nums[idx - 1],注意这里不要使用nums[--idx],因为这样会改变idx的值,导致索引不正确),如果相等则i++,继续向后遍历,如果不相等则加入到结果数组中(这里可以这样做的原因是nums是有序数组!!!如果是无序数组则不能这么做),下面是一个模拟的例子:

视频讲解点击视频讲解-删除有序数组中的重复项 Ⅱ
时间复杂度:
时间复杂度为O(n),其中n为数组的长度。
代码实现:
class Solution {public int removeDuplicates(int[] nums) {if(nums.length <= 2) return nums.length;int idx = 1;for(int i = 2;i < nums.length ; i++){if(nums[i] != nums[idx - 1]){nums[++idx] = nums[i];}}return idx + 1;}
}
2.相向双指针
双指针 一般是一个在开头,一个在结尾,两者相向处理问题,一般用来确定某个符合条件的子数组,需要维护左右边界。
2.1例题
11.盛最多水的容器
思路:
本题采用双指针来求解,由于盛水的体积为宽✖高,因此可以定义首尾两个指针,枚举出不同高度的体积并取最大值,在移动指针的过程中,应该移动高度较小的指针,因为盛水的高度是由短板来决的,如图,不同的颜色表示每次移动指针后得到的体积。视频讲解点击视频讲解-盛最多水的容器。

时间复杂度:
时间复杂度为O(n),空间复杂度O(1)。
代码实现:
class Solution {public int maxArea(int[] height) {int ans = 0;int l = 0;int r =height.length - 1;while(l < r){ans = Math.max(ans,Math.min(height[l],height[r]) * (r-l));if(height[l] < height[r]) l++;else r--;}return ans;}
}
42.接雨水
思路:
本题采用双指针来求解,类似于11.盛水最多的容器,盛水的多少取决于左右柱子里较低的一个。通过维护左边和右边的最大高度,来计算整个数组中的装水容量,定义两个变量lmax和rmax,初始值都为0,用于记录当前位置左边和右边的最大高度,不断更新左右两边的最大高度来计算每个位置的水位,然后将各个位置的水位差累加起来得到总的装水容量,下面是一个模拟的例子:

视频讲解点击视频讲解-接雨水。
时间复杂度:
这段代码的时间复杂度是O(n),其中n是height数组的长度。由于只使用了一个while循环来遍历height,没有嵌套的循环,因此时间复杂度是线性的。
代码实现:
class Solution {public int trap(int[] height) {int l = 0;int r = height.length - 1;int lmax = 0;int rmax = 0;int ans = 0;while(l < r){lmax = Math.max(lmax,height[l]);rmax = Math.max(rmax,height[r]);if(lmax < rmax){ans += lmax - height[l];l++;} else{ans += rmax - height[r];r--;}}return ans;}
}
581.最短无序连续子数组
思路:
本题采用双指针解决,分别从数组的两端进行遍历,确定结果数组的左右边界。确定左边界的条件如果当前元素小于左边界处的最大值,则更新右边界,否则更新左边界的最大值(左边界的右边不应该出现比左边界小的值);确定右边界的条件是如果当前元素大于右边界处的最小值,则更新左边界,否则更新右边界的最小值(右边界的左边不应该出现比右边界大的值),得到左右边界后返回子数组的长度即可。
时间复杂度:
时间复杂度为O(n),n为数组长度。
代码实现:
class Solution {public int findUnsortedSubarray(int[] nums) {//初始化工作://start、end分别是从前向后和从后向前遍历数组的两个指针//需要注意的是end不是从len - 1开始,初始值应该为-1,这是为了处理数组本来就是有序数组的情况//lmax、rmin分别是遍历过程中维护的左边界的最大值和右边界的最小值int len = nums.length;int start = 0;int end = -1;int lmax = nums[0];int rmin = nums[len - 1]; for(int i = 0;i < len ; i++){//确定左边界if(nums[i] < lmax){end = i;} else {lmax = nums[i];}//确定右边界if(nums[len - i - 1] > rmin){start = len - i -1;} else {rmin = nums[len - i -1];}}return end - start + 1;}
}
参考资料:双指针-数组
相关文章:

leetCode-hot100-数组专题之双指针
数组双指针专题 1.同向双指针1.1例题26.删除有序数组中的重复项27.移除元素80.删除有序数组中的重复项 Ⅱ 2.相向双指针2.1例题11.盛最多水的容器42.接雨水581.最短无序连续子数组 双指针在算法题中很常见,下面总结双指针在数组中的一些应用,主要分为两类…...
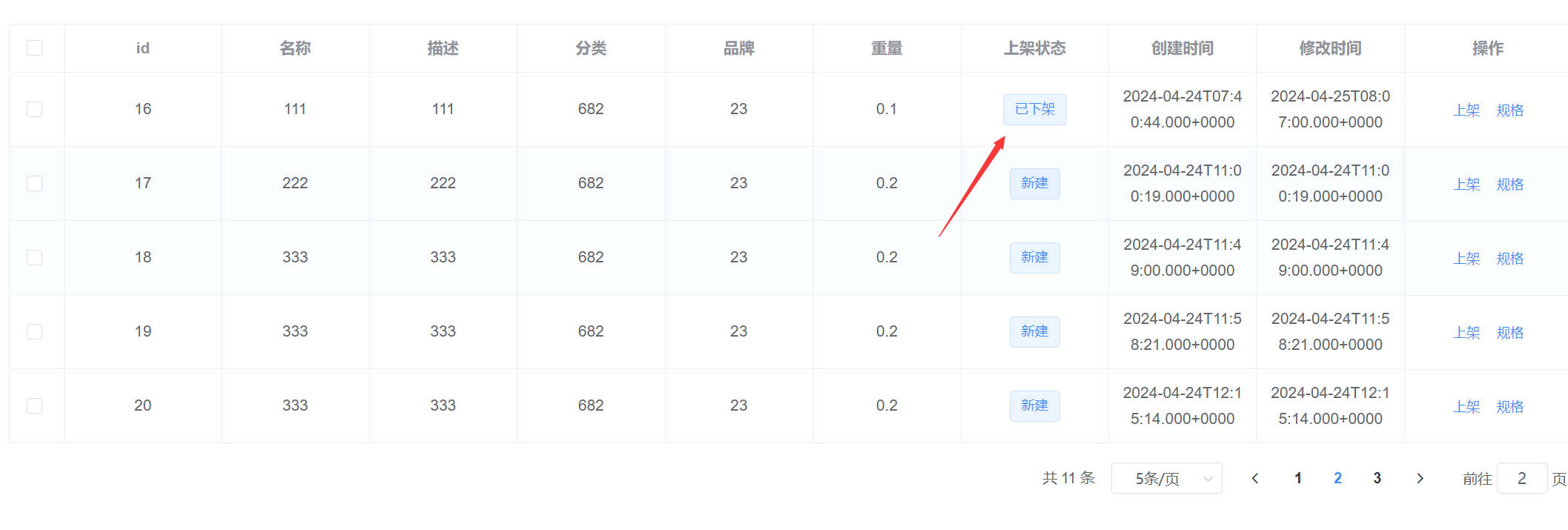
完成商品SPU管理页面
文章目录 1.引入前端界面1.将前端界面放到commodity下2.创建菜单3.进入前端项目,使用npm添加依赖1.根目录下输入2.报错 chromedriver2.27.2的问题3.点击链接下载压缩包,然后使用下面的命令安装4.再次安装 pubsub-js 成功5.在main.js中引入这个组件 4.修改…...
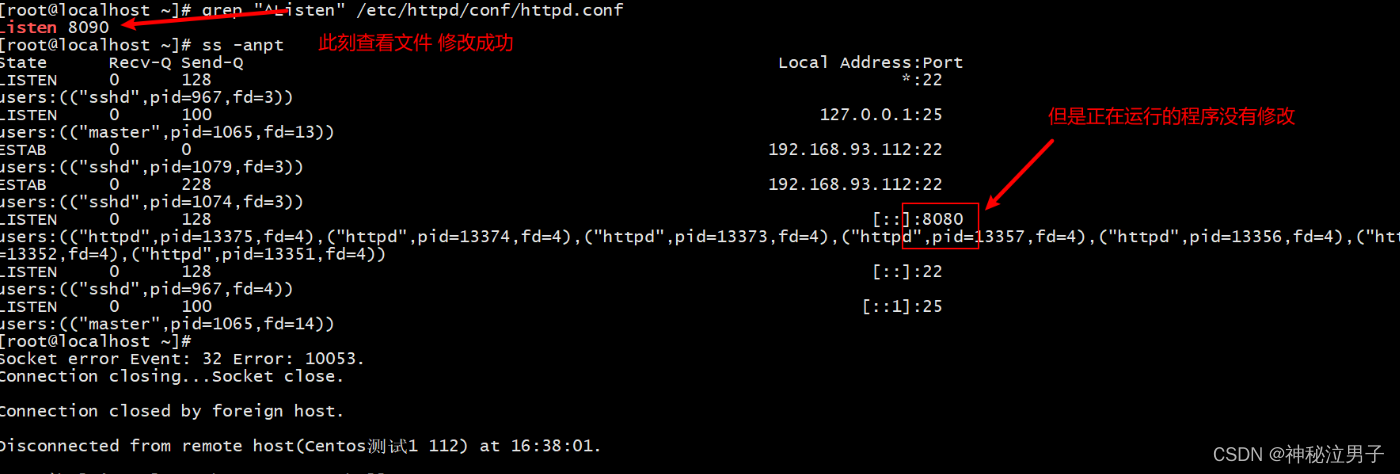
Ansible实战YAML语言完成apache的部署,配置,启动全过程
🏡作者主页:点击! 🏝️Ansible专栏:点击! ⏰️创作时间:2024年5月24日15点59分 目录 💯趣站推荐💯 🎊前言 ✨️YAML语言回顾 🎆1.编写YAML文…...

深入探索微软Edge:新一代浏览器的演进与创新
在数字时代的浪潮中,浏览器已不再只是简单的网页访问工具,而是成为了连接信息、服务与用户之间的重要桥梁。微软Edge作为微软公司推出的一款全新的浏览器,不仅承载着微软在互联网领域的最新愿景,还融合了多项前沿技术,…...

k8s使用Volcano调度gpu
k8s部署 https://www.yangxingzhen.com/9817.html cri-dockerd安装 https://zhuanlan.zhihu.com/p/632861515 安装nvidia-container-runtime https://docs.nvidia.com/datacenter/cloud-native/container-toolkit/latest/install-guide.html 安装k8s-device-plugin https://…...

x的平方根-力扣
本题想到使用二分法不断逼近一个区间,直到最后趋近于x,从而求得解。注意的点,一开始使用 if(mid * mid < x) 进行判断时,会出现越界,原因是输入一个很大的数是,超过int表示的范围,继而修改为…...
hot100 -- 回溯(上)
目录 🍞科普 🌼全排列 AC DFS 🚩子集 AC DFS 🎂电话号码的字母组合 AC DFS 🌼组合总和 AC DFS 🍞科普 忘记 dfs 的,先看看这个👇 DFS(深度优先搜索…...

5.24数据库作业
考虑如下关系模式R(A,B.C.D,E,F)上的函数依赖集F: {A→BCD,BC→DE,B→D,D→A} 1、计算B的闭包。 2、(使用Armstrong公理)证明AF是超码。 3、计算上述函数依赖集F的正则覆盖;给出你的推导的步骤并解释。 4、基于正则覆盖࿰…...

go-zero 实战(5)
引入Prometheus 用 Prometheus 监控应用 1. 用 docker 启动 Prometheus 编辑配置位置,我将 prometheus.yaml 和 targets.json 文件放在了 /opt/prometheus/conf目录下 prometheus.yaml global:scrape_interval: 15s # 抓取间隔evaluation_interval: 15s # 评估…...

Python异常处理:打造你的代码防弹衣!
Hi,我是阿佑,上文咱们讲到——揭秘Python的魔法:装饰器的超能力大揭秘 ♂️✨,阿佑将带领大家通过精准捕获异常、使用with语句和上下文管理器、以及异常链等高级技巧来增强代码的健壮性。就像为代码穿上防弹衣,保护它…...

Linux——进程与线程
进程与线程 前言一、Linux线程概念线程的优点线程的缺点线程异常线程用途 二、Linux进程VS线程进程和线程 三、Linux线程控制创建线程线程ID及进程地址空间布局线程终止线程等待分离线程 四、习题巩固请简述什么是LWP请简述LWP与pthread_create创建的线程之间的关系简述轻量级进…...

ping 探测网段哪些地址被用
#!/bin/bash# 遍历192.168.3.1到192.168.3.254 for i in {1..254} doip"192.168.3.$i"# 对每个IP地址进行三次ping操作if ping -c 3 -W 1 $ip > /dev/null 2>&1thenecho "$ip: yes"fi done$ sh test.sh 192.168.3.1: yes 192.168.3.95: yes 192.…...
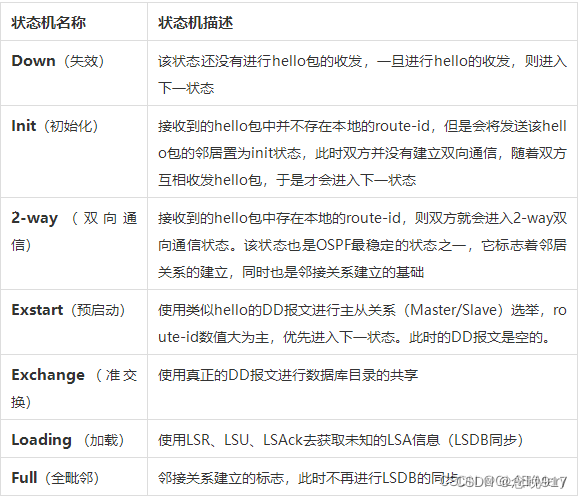
OSPF问题
.ospf 选路 域内 --- 1类,2类LSA 域间 --- 3类LSA 域外 --- 5类,7类LSA --- 根据开销值的计算规则不同,还分为类型1和类型2 ospf 防环机制 区域内防环:在同一OSPF区域内,所有路由器通过交换链路状态通告ÿ…...

asgasgas
asdgasdgsa...

Go语言实现人脸检测(Go的OpenCV绑定库)
文章目录 OpenCVGithub官网安装环境变量 Go的OpenCV绑定库Github文档安装搜索视频设备ID显示视频检测人脸 OpenCV Github https://github.com/opencv/opencv/ 官网 https://opencv.org/ 安装 brew install opencv brew upgrade opencv安装目录 cd /usr/local/opt/opencv…...

springboot中线程池的使用
一、概念 线程池就是将多个线程对象放入一个池子里面,例如一个池塘,线程池就是这个池塘,池塘里面的鱼就是线程池中的多个线程对象。1. 每一个线程,在一段时间内只能执行一个任务。2. 线程池中的各个线程是可以重复使用的。 二、创…...

ubuntu20.04 开机自动挂载外加硬盘
文章目录 一、问题描述二、操作1. 查找新添盘符2. 格式化硬盘文件系统3. 挂载硬盘4. 开机自动挂载5. 取消挂载6. 查看挂载的硬盘信息 一、问题描述 因电脑使用一段时间后自身硬盘不足,需外加硬盘使得电脑自动识别加载。 二、操作 1. 查找新添盘符 sudo blkid自己…...
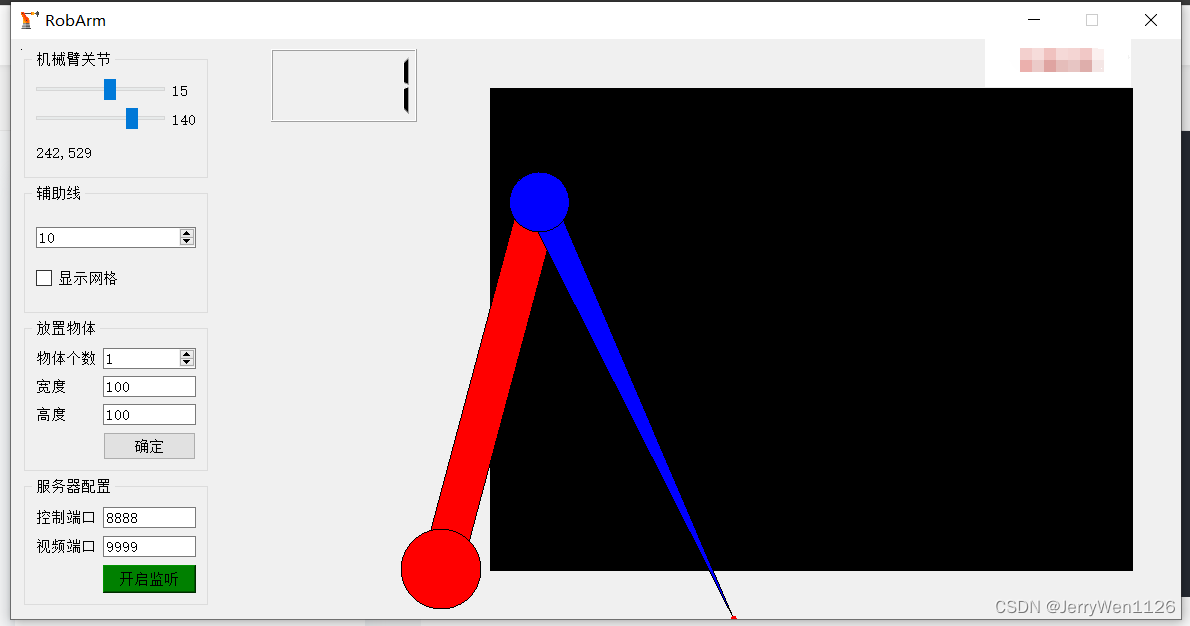
5.18 TCP机械臂模拟
#include <netinet/tcp.h>//包含TCP选项的头文件 #include <arpa/inet.h> #include <stdio.h> #include <stdlib.h> #include <unistd.h> #include <linux/input.h>//读取输入事件 #include <sys/types.h> #include <sys/stat.h&…...
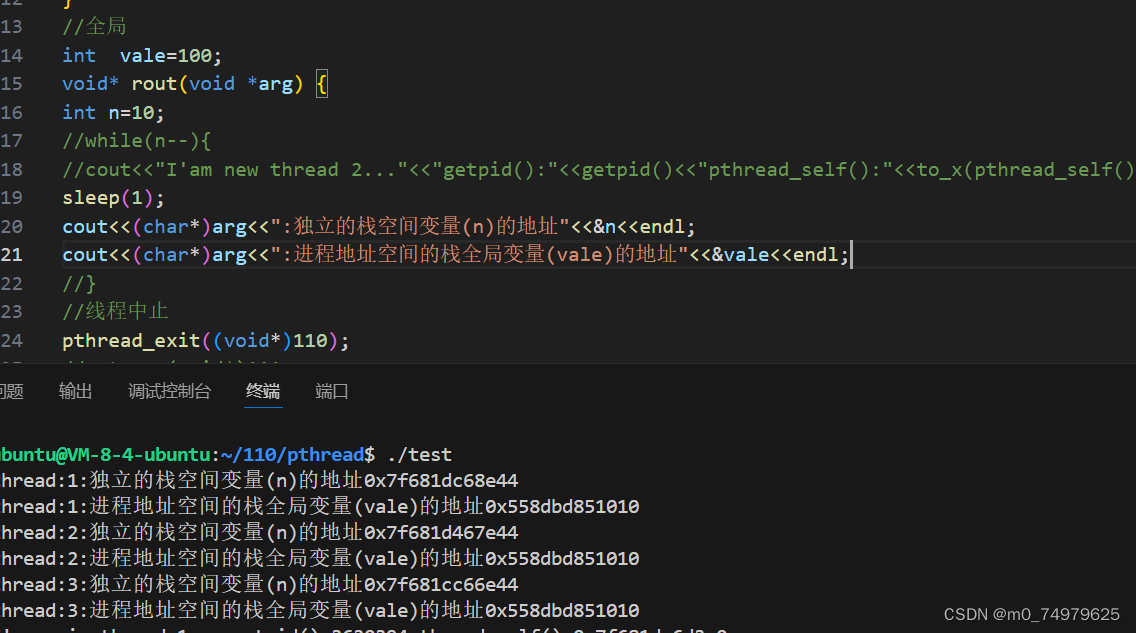
linux---线程控制
线程和进程 以前我们要同时跑多个程序,可以通过fork()多个子进程,然后通过系统函数进行程序的替换,但是创建进程代价大,不仅要拷贝一份父进程的地址空间,页表,文件表述符表等。但是线程不需要因为是进程的…...
低代码开发:拖拽式可视化构建工业物联网系统
什么是低代码? 低代码(Low Code)是一种可视化的软件开发方法,通过最少的手动编码可以更快地交付应用程序。低代码平台的图形用户界面和拖放功能可自动执行开发过程的各个方面,从而消除对传统计算机编程方法的依赖。 什么是低代码平台&#…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...
