其它高阶数据结构⑦_Skiplist跳表_概念+实现+对比
目录
1. Skiplist跳表的概念
2. Skiplist跳表的效率
3. Skiplist跳表的实现
3.1 力扣1206. 设计跳表
3.2 Skiplist的初始化和查找
3.3 Skiplist的增加和删除
3.4 Skiplist的源码和OJ测试
4. 跳表和平衡搜索树/哈希表的对比
本篇完。
1. Skiplist跳表的概念
skiplist是由美国计算机科学家William Pugh(威廉 普格)于1989年发明。skiplist本质上是一种查找结构,用于解决算法中的查找问题,跟平衡搜索树和哈希表的价值是 一样的,可以作为key或者key/value的查找模型。skiplist,顾名思义,首先它是一个list。实际上,它是在有序链表的基础上发展起来的。我们知道在对一个有序链表进行查找,它的时间复杂度为O(N)。
William Pugh开始了他的优化思路:
假如我们每相邻两个节点升高一层,增加一个指针,让指针指向下下个节点,如下图所示:
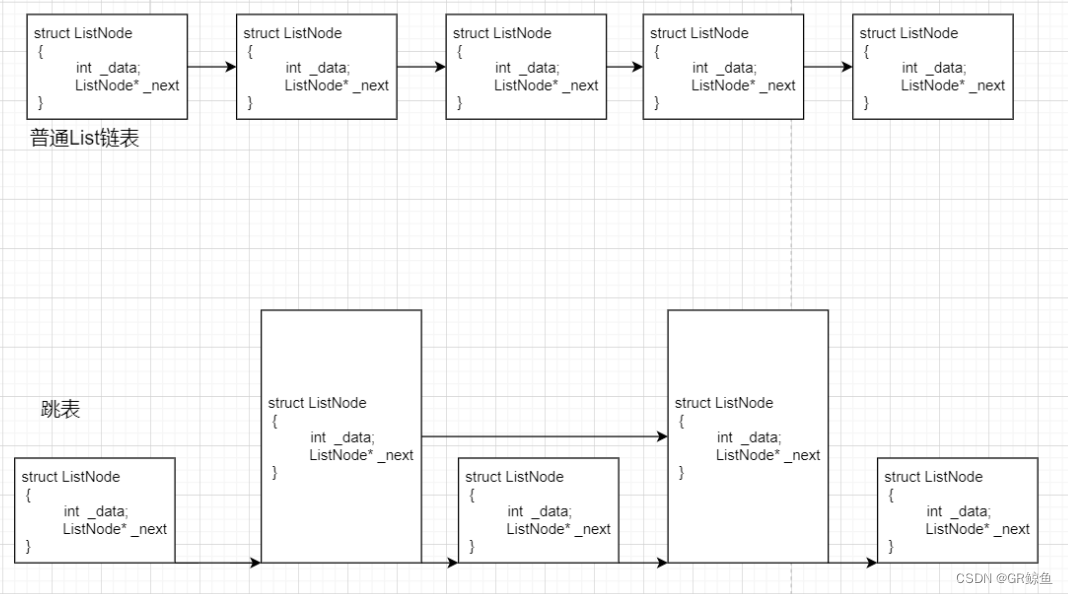
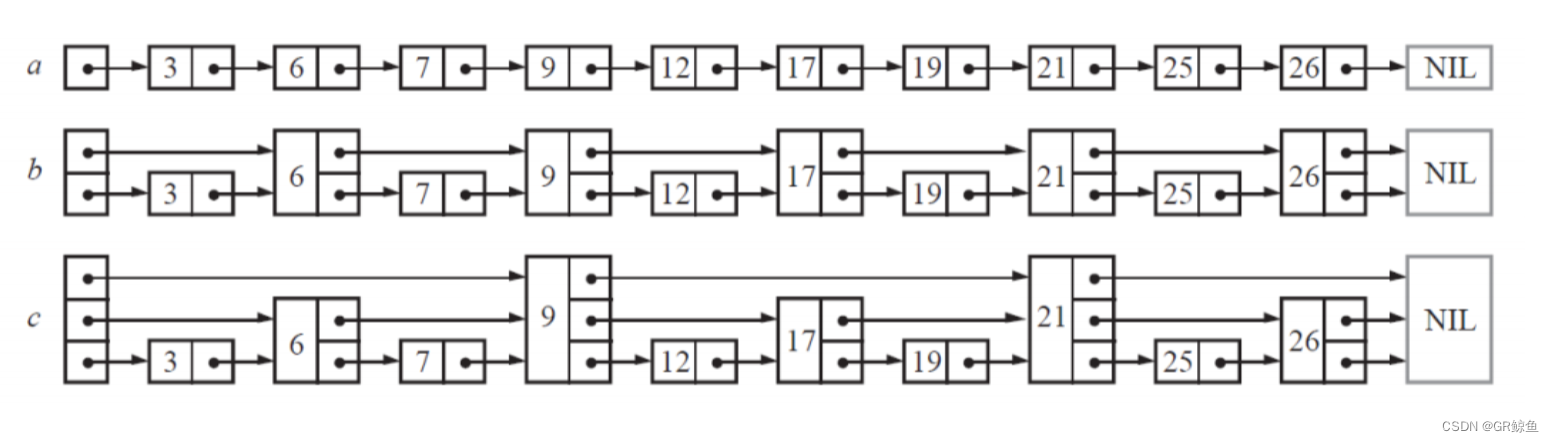
这样新增的一层指针通过连接可以形成新的链表,它包含了整个链表节点的一半,由此需要在这一层进行比较、筛除的个数也就降低了一半。
以此类推,继续增加一层指针,新链表的节点数下降,查找的效率自然而然也就提高了。按照上述每增加一层,节点数就少一半,其查找的过程类似于二分查找,使得查找的时间复杂度可以降低到O(logN)。
上述查找的前提是一个有序的链表。无论是对其中的链表新增节点,还是删除节点,都可能打乱原有维持的指针连接,从而导致跳表失效。如果要维持这种对应关系,就必须把新插入的节点后面的所有节点(也包括新插入的节点)重新进行调整,这会让时间复杂度重新退化成O(N)。
随机层数: 为了避免这种情况,skiplist的设计不再严格要求对应比例关系,而是插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数。
2. Skiplist跳表的效率
那么skiplist在引入随机层数后,如何保证其查找效率呢?首先,这个随机层数会有一个限制,这里把它叫做maxLevel,其次会设置一个多增加一层的概率p。那么计算这个随机层数的伪代码如下图:

在Redis的skiplist实现中,这两个参数的取值为:p = 1/4,maxLevel = 32。
根据前面randomLevel()的伪码,很容易看出,产生越高的节点层数,概率越低。定量的分析如下:
- 节点层数至少为1。而大于1的节点层数,满足一个概率分布。
- 节点层数恰好等于1的概率为1-p。
- 节点层数大于等于2的概率为p,而节点层数恰好等于2的概率为p(1-p)。
- 节点层数大于等于3的概率为p^2,而节点层数恰好等于3的概率为p^2*(1-p)。
- 节点层数大于等于4的概率为p^3,而节点层数恰好等于4的概率为p^3*(1-p)。
- ......
最终可以得到这样一个数学式,用于计算一个节点的平均层数:
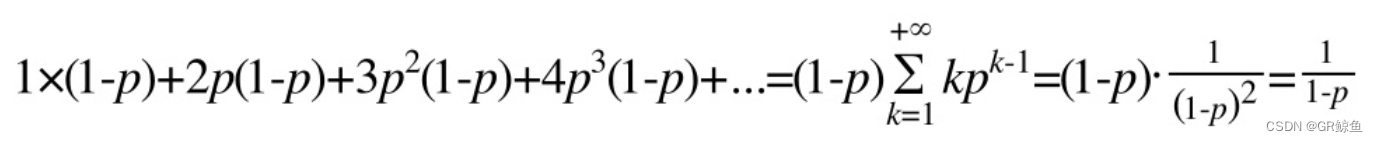
有了这个公式,我们可以很容易计算出:
当 p = 1/2 时: 每个节点所包含的平均指针数目为2。
当 p = 1/4 时: 每个节点所包含的平均指针数目为1.33。
至于跳表的平均时间复杂度为O(logN)的证明,这推导的过程较为复杂,下面的两篇中英文章有详细讲解:
铁蕾大佬的博客:Redis内部数据结构详解(6)——skiplist - 铁蕾的个人博客
William_Pugh大佬的论文:http://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf
3. Skiplist跳表的实现
力扣上有一道实现跳表的题,可以在这上面完成跳表的测试:
3.1 力扣1206. 设计跳表
1206. 设计跳表
难度 困难
不使用任何库函数,设计一个 跳表 。
跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。
例如,一个跳表包含 [30, 40, 50, 60, 70, 90] ,然后增加 80、45 到跳表中,以下图的方式操作:
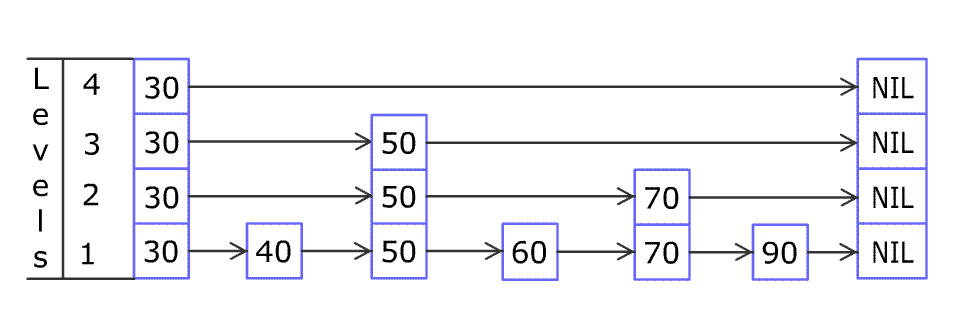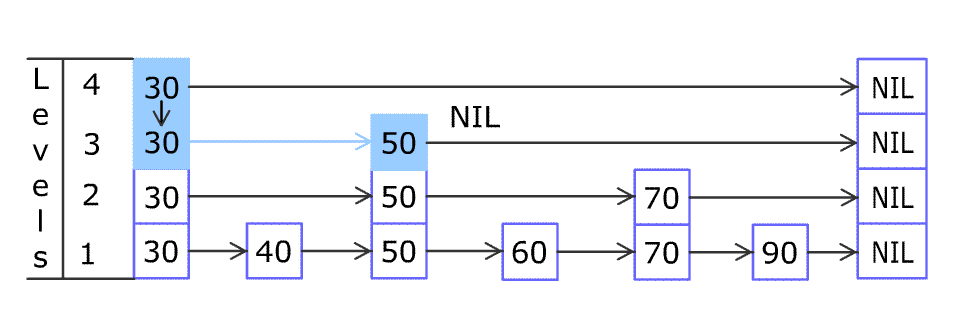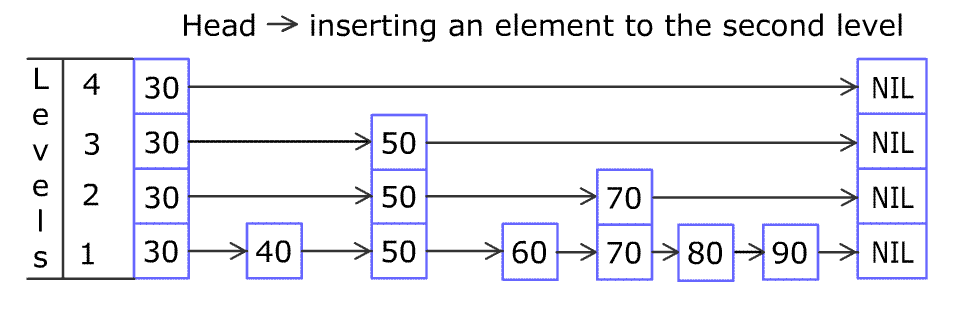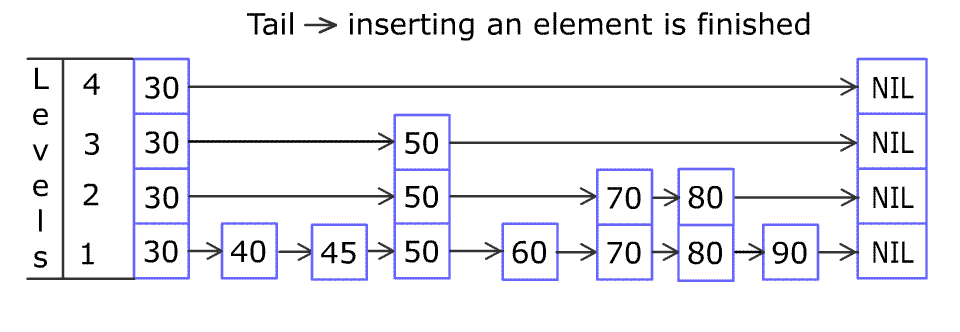
跳表中有很多层,每一层是一个短的链表。在第一层的作用下,增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n)),空间复杂度是 O(n)。
了解更多 : 跳表 - OI Wiki
在本题中,你的设计应该要包含这些函数:
bool search(int target): 返回target是否存在于跳表中。void add(int num): 插入一个元素到跳表。bool erase(int num): 在跳表中删除一个值,如果num不存在,直接返回false. 如果存在多个num,删除其中任意一个即可。
注意,跳表中可能存在多个相同的值,你的代码需要处理这种情况。
示例 1:
输入 ["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"] [[], [1], [2], [3], [0], [4], [1], [0], [1], [1]] 输出 [null, null, null, null, false, null, true, false, true, false]解释 Skiplist skiplist = new Skiplist(); skiplist.add(1); skiplist.add(2); skiplist.add(3); skiplist.search(0); // 返回 false skiplist.add(4); skiplist.search(1); // 返回 true skiplist.erase(0); // 返回 false,0 不在跳表中 skiplist.erase(1); // 返回 true skiplist.search(1); // 返回 false,1 已被擦除
提示:
0 <= num, target <= 2 * 10^4- 调用
search,add,erase操作次数不大于5 * 10^4
class Skiplist {
public:Skiplist() {}bool search(int target) {}void add(int num) {}bool erase(int num) {}
};/*** Your Skiplist object will be instantiated and called as such:* Skiplist* obj = new Skiplist();* bool param_1 = obj->search(target);* obj->add(num);* bool param_3 = obj->erase(num);*/3.2 Skiplist的初始化和查找
Skiplist的初始化:
跳表不仅仅是要存储数据 _data,还需要有next指针,当然这些next指针也不止一个 这取决于当前节点的层数。

结合此图就可以知道next指针应该在一个数组中:
class SkiplistNode
{
public:int _val;vector<SkiplistNode*> _nextV;SkiplistNode(int val, int level):_val(val), _nextV(level, nullptr){}
};class Skiplist
{
private:typedef SkiplistNode Node;Node* _head;size_t _maxLevel = 32;double _p = 0.5;
public:Skiplist(){_head = new SkiplistNode(-1, 1); // 头节点,层数是1}
}Skiplist的search查找:
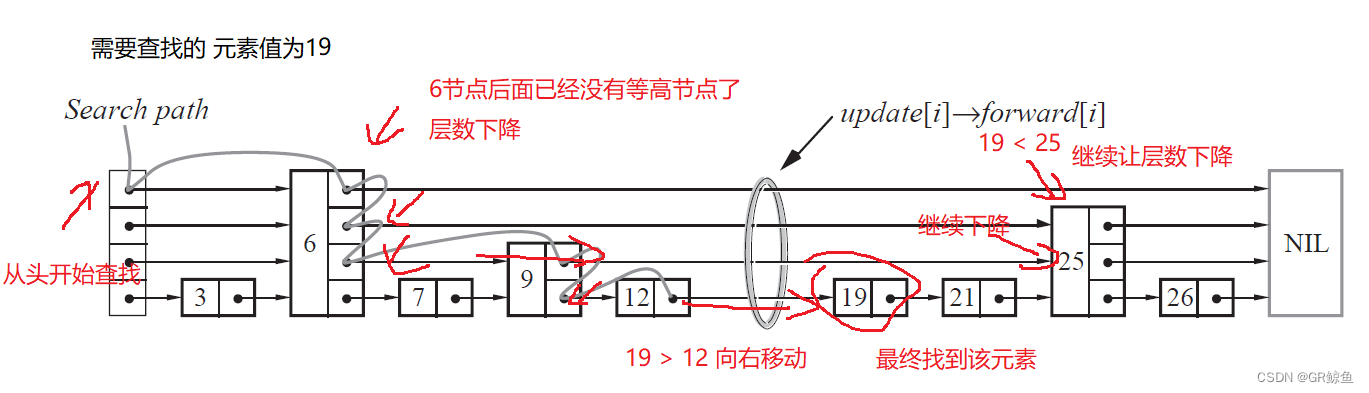
查找的过程:查找是要和下一个节点的值相比,并不是和当前节点的值相比一开始cur在哨兵位头节点的最高层 head,开始进行比较。设要查找的值为target,如果下一个节点为空或者下一个节点的值比target大,那么cur需要向下一层走,如果下一个节点的值比targe小,那么cur向右走。重复上述过程,直至找到或者没找到(没找到的话,cur会到第-1层,层数是从第0层开始的)
bool search(int target){Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){if (cur->_nextV[level] && cur->_nextV[level]->_val < target){cur = cur->_nextV[level]; // 目标值比下一个节点值要大,向右走}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target){--level; //下一个节点是空(尾),或目标值比下一个节点值要小,向下走}else{return true;}}return false;}3.3 Skiplist的增加和删除
Skiplist的add增加:
假设要增加17,要怎么操作?

- 获得这个结点的层数:RandomLevel( );
- 找到这个结点的前后链接关系(此过程就像查找这个结点每一层的前一个结点,后面的删除结点也需要用到,所以封装成一个FindPrevNode函数):比如查找17的话就是prev_val < 17 < next_val,需要从头结点开始找,记录每一层的前一个指针。
Skiplist(){srand(time(nullptr)); // 构造函数种下随机数种子_head = new SkiplistNode(-1, 1); // 头节点,层数是1}vector<Node*> FindPrevNode(int num){Node* cur = _head;int level = _head->_nextV.size() - 1;vector<Node*> prevV(level + 1, _head); // 插入位置每一层前一个节点指针while (level >= 0){if (cur->_nextV[level] && cur->_nextV[level]->_val < num){cur = cur->_nextV[level]; // 目标值比下一个节点值要大,向右走}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num){prevV[level] = cur; // 更新level层前一个--level; //下一个节点是空(尾),目标值比下一个节点值要小,向下走}}return prevV;}void add(int num){vector<Node*> prevV = FindPrevNode(num);int n = RandomLevel();Node* newnode = new Node(num, n);if (n > _head->_nextV.size()) // 如果n超过当前最大的层数,那就升高一下_head的层数{_head->_nextV.resize(n, nullptr);prevV.resize(n, _head);}for (size_t i = 0; i < n; ++i) // 链接前后节点{newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}}int RandomLevel(){size_t level = 1; // rand() ->[0, RAND_MAX]之间while (rand() <= RAND_MAX * _p && level < _maxLevel){++level;}return level;}这里的RandomLevel()是以一种巧妙的方式完成的:
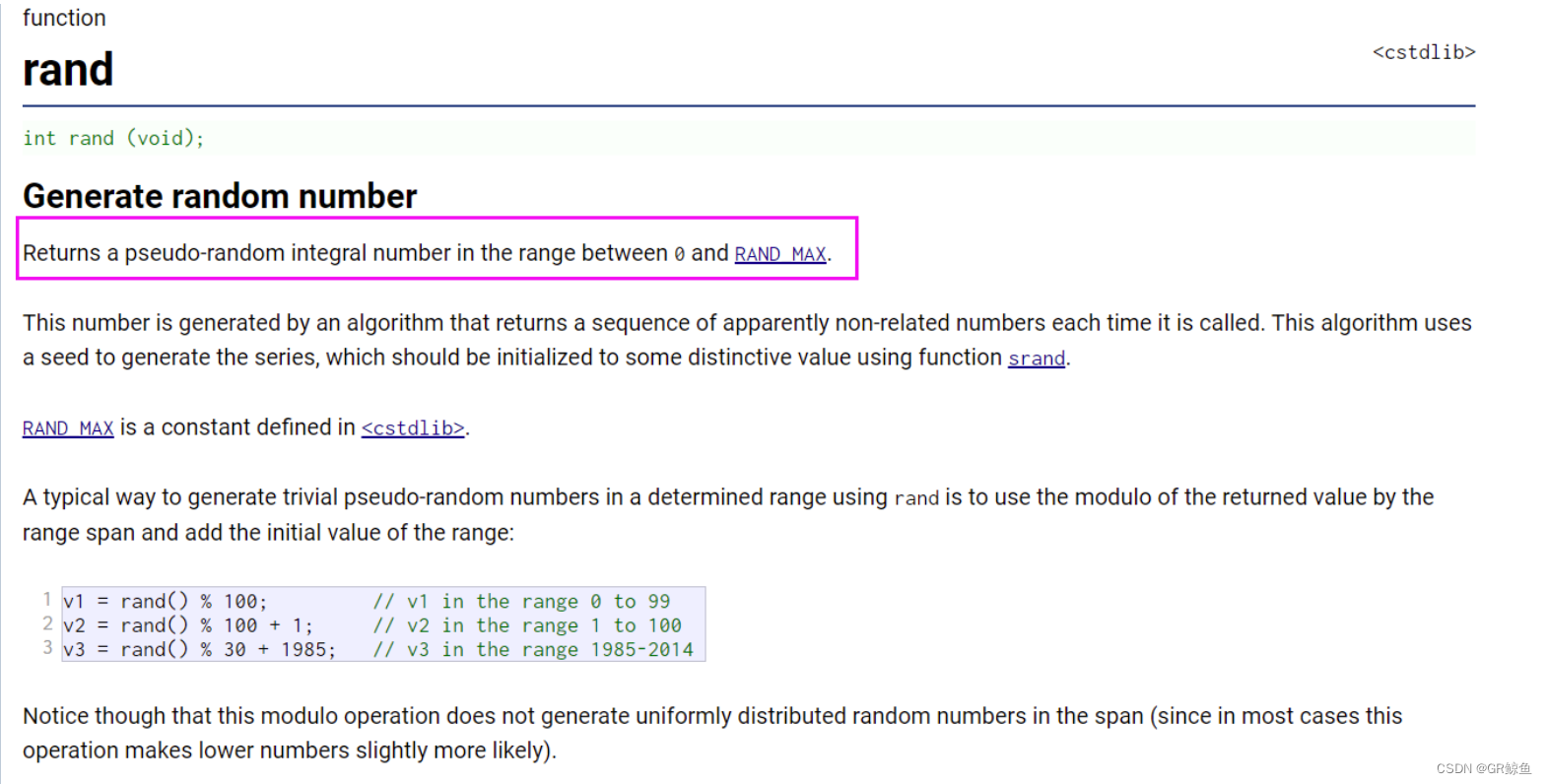
通过_p可以控制最终值产生范围的概率。如_p是0.5的话,生成的随机数小于RAND_MAX的一半才可能增加层数。
Skiplist的erase删除:
删除怎么操作?假设现在要删除17:

删除的操作和增加的操作几乎一样,通过FindPrevNode找到该结点的所有前驱结点,让所有前驱结点指向被删除结点的next即可。
bool erase(int num){vector<Node*> prevV = FindPrevNode(num);if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num){return false; // 第一层下一个不是val,val不在表中}else{Node* del = prevV[0]->_nextV[0];for (size_t i = 0; i < del->_nextV.size(); i++) // del节点每一层的前后指针链接起来{prevV[i]->_nextV[i] = del->_nextV[i];}delete del;int i = _head->_nextV.size() - 1; // 如果删除最高层节点,把头节点的层数降一下while (i >= 0){if (_head->_nextV[i] == nullptr)--i;elsebreak;}_head->_nextV.resize(i + 1);return true;}}3.4 Skiplist的源码和OJ测试
class SkiplistNode
{
public:int _val;vector<SkiplistNode*> _nextV;SkiplistNode(int val, int level):_val(val), _nextV(level, nullptr){}
};class Skiplist
{
private:typedef SkiplistNode Node;Node* _head;size_t _maxLevel = 32;double _p = 0.5;
public:Skiplist(){srand(time(nullptr)); // 构造函数种下随机数种子_head = new SkiplistNode(-1, 1); // 头节点,层数是1}bool search(int target){Node* cur = _head;int level = _head->_nextV.size() - 1;while (level >= 0){if (cur->_nextV[level] && cur->_nextV[level]->_val < target){cur = cur->_nextV[level]; // 目标值比下一个节点值要大,向右走}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target){--level; //下一个节点是空(尾),或目标值比下一个节点值要小,向下走}else{return true;}}return false;}vector<Node*> FindPrevNode(int num){Node* cur = _head;int level = _head->_nextV.size() - 1;vector<Node*> prevV(level + 1, _head); // 插入位置每一层前一个节点指针while (level >= 0){if (cur->_nextV[level] && cur->_nextV[level]->_val < num){cur = cur->_nextV[level]; // 目标值比下一个节点值要大,向右走}else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num){prevV[level] = cur; // 更新level层前一个--level; //下一个节点是空(尾),目标值比下一个节点值要小,向下走}}return prevV;}void add(int num){vector<Node*> prevV = FindPrevNode(num);int n = RandomLevel();Node* newnode = new Node(num, n);if (n > _head->_nextV.size()) // 如果n超过当前最大的层数,那就升高一下_head的层数{_head->_nextV.resize(n, nullptr);prevV.resize(n, _head);}for (size_t i = 0; i < n; ++i) // 链接前后节点{newnode->_nextV[i] = prevV[i]->_nextV[i];prevV[i]->_nextV[i] = newnode;}}int RandomLevel(){size_t level = 1; // rand() ->[0, RAND_MAX]之间while (rand() <= RAND_MAX * _p && level < _maxLevel){++level;}return level;}bool erase(int num){vector<Node*> prevV = FindPrevNode(num);if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num){return false; // 第一层下一个不是val,val不在表中}else{Node* del = prevV[0]->_nextV[0];for (size_t i = 0; i < del->_nextV.size(); i++) // del节点每一层的前后指针链接起来{prevV[i]->_nextV[i] = del->_nextV[i];}delete del;int i = _head->_nextV.size() - 1; // 如果删除最高层节点,把头节点的层数降一下while (i >= 0){if (_head->_nextV[i] == nullptr)--i;elsebreak;}_head->_nextV.resize(i + 1);return true;}}
};/*** Your Skiplist object will be instantiated and called as such:* Skiplist* obj = new Skiplist();* bool param_1 = obj->search(target);* obj->add(num);* bool param_3 = obj->erase(num);*/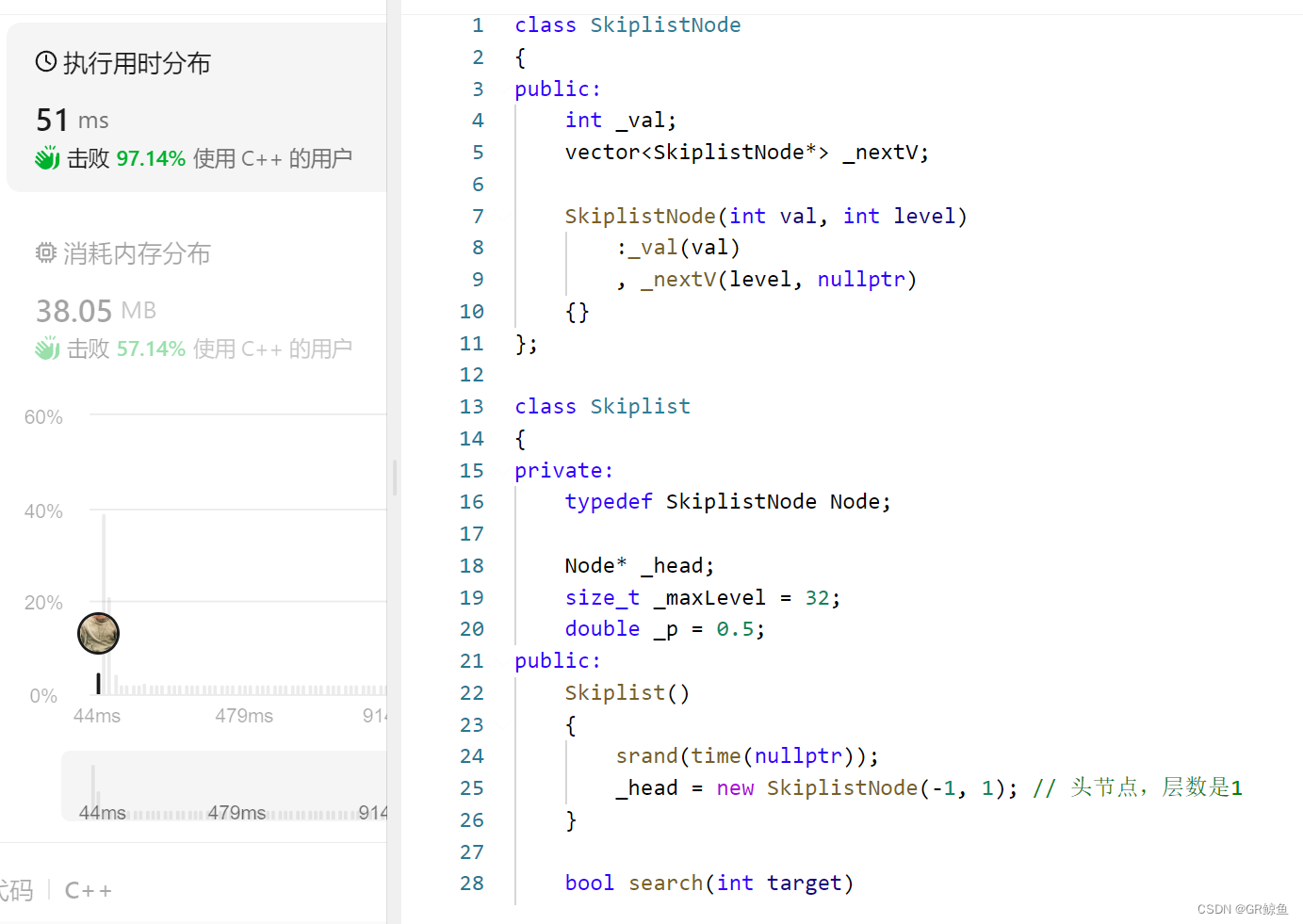
4. 跳表和平衡搜索树/哈希表的对比
跳表和平衡搜索树的对比:
跳表相比平衡搜索树(AVL树和红黑树)对比都可以做到遍历数据有序,时间复杂度也差不多,都是O(logN)。不过跳表与平衡搜索树相比,跳表的优势在于:
- 跳表实现简单,容易控制。平衡树增删查改遍历都更复杂。
- 跳表的额外空间消耗更低。平衡树节点存储每个值有三叉链,平衡因子/颜色等消耗。可是跳表可以通过p来调整每个节点的指针个数,那是个可接受的数量。
跳表和哈希表的对比:
跳表相比哈希表而言,跳表在查找效率上更差一点。哈希表平均时间复杂度是O(1),比跳表的O(logN)快。
skiplist与哈希表相比,skiplist的优势在于:
- 遍历数据有序。
- skiplist空间消耗略小一点,哈希表存在链接指针和表空间消耗。
- 哈希表在极端场景下哈希冲突高,效率下降厉害,需要红黑树补足接力。
本篇完。
高阶数据结构到这先暂告一段落了。
相关文章:

其它高阶数据结构⑦_Skiplist跳表_概念+实现+对比
目录 1. Skiplist跳表的概念 2. Skiplist跳表的效率 3. Skiplist跳表的实现 3.1 力扣1206. 设计跳表 3.2 Skiplist的初始化和查找 3.3 Skiplist的增加和删除 3.4 Skiplist的源码和OJ测试 4. 跳表和平衡搜索树/哈希表的对比 本篇完。 1. Skiplist跳表的概念 skiplist是…...

力扣230. 二叉搜索树中第K小的元素
Problem: 230. 二叉搜索树中第K小的元素 文章目录 题目描述思路复杂度Code 题目描述 思路 直接利用二叉搜索树中序遍历为一个有序序列的特性: 记录一个int变量rank,在中序遍历时若当前rank k则返回当前节点值 复杂度 时间复杂度: O ( n ) O(n) O(n);其…...

Linux_应用篇(07) 系统信息与系统资源
在应用程序当中,有时往往需要去获取到一些系统相关的信息,譬如时间、日期、以及其它一些系统相关信息,本章将向大家介绍如何通过 Linux 系统调用或 C 库函数获取系统信息, 譬如获取系统时间、日期以及设置系统时间、日期等&#x…...
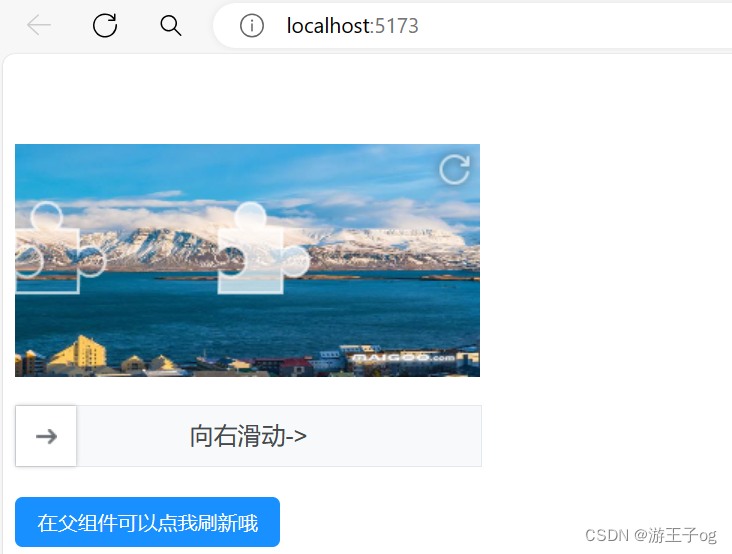
基于Vue的验证码实现
一、验证码核心实现 创建slide-verify.vue,代码如下: <template><divclass"slide-verify":style"{ width: w px }"id"slideVerify"onselectstart"return false;"><!-- 图片加载遮蔽罩 -->&…...

P4【力扣217,389,496】【数据结构】【哈希表】C++版
【217】存在重复元素 给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。 示例 1: 输入:nums [1,2,3,1] 输出:true 示例 2:…...

PE文件(六)新增节-添加代码作业
一.手动新增节添加代码 1.当预备条件都满足,节表结尾没有相关数据时: 现在我们将ipmsg.exe用winhex打开,在节的最后新增一个节用于存放我们要增加的数据 注意:飞鸽的文件对齐和内存对齐是一致的 先判断节表末尾到第一个节之间…...

ICRA 2024: NVIDIA 联合多伦多大学、加州大学伯克利分校、苏黎世联邦理工学院等研究人员开发了精细操作的手术机器人
英伟达(NVIDIA)正与学术研究人员合作,研究手术机器人。 NVIDIA 联合多伦多大学、加州大学伯克利分校、苏黎世联邦理工学院和佐治亚理工学院的研究人员开发了 ORBIT-Surgical,一个训练机器人的模拟框架,可以提高手术团…...

探索Go语言的原子操作秘籍:sync/atomic.Value全解析
引言 在并发编程的世界里,数据的一致性和线程安全是永恒的话题。Go语言以其独特的并发模型——goroutine和channel,简化了并发编程的复杂性。然而,在某些场景下,我们仍然需要一种机制来保证操作的原子性。这就是sync/atomic.V…...

【java深入学习第3章】利用 Spring Boot 和 Screw 快速生成数据库设计文档
免费多模型AI网站,支持豆包、GPT-4o、谷歌Gemini等AI模型,无限制使用,快去白嫖👉海鲸AI🔥🔥🔥 在开发过程中,数据库设计文档是非常重要的,它可以帮助开发者理解数据库结构࿰…...
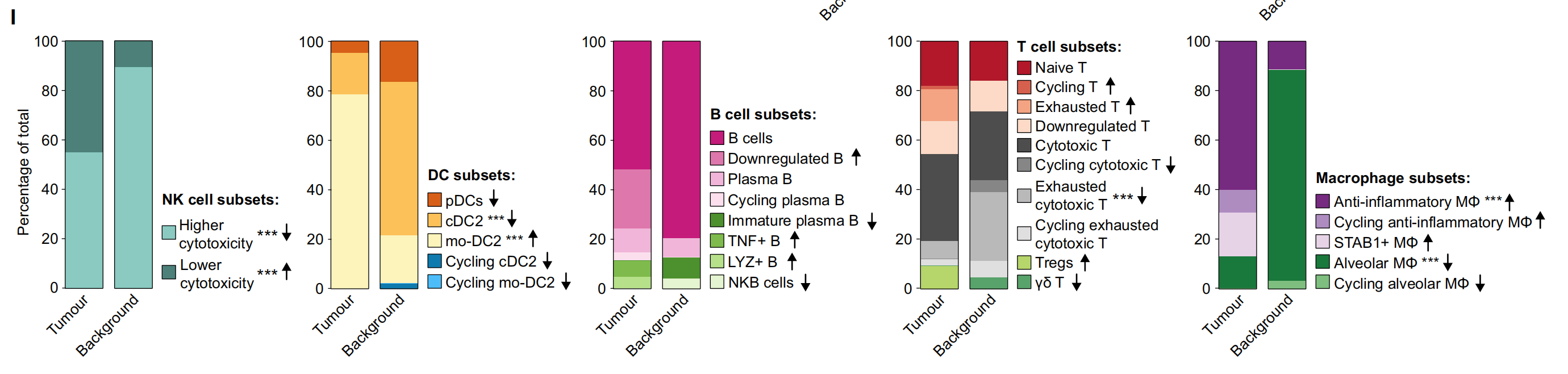
继“三级淋巴结”之后,再看看“单细胞”如何与AI结合【医学AI|顶刊速递|05-25】
小罗碎碎念 24-05-25文献速递 今天想和大家分享的是肿瘤治疗领域的另一个热点——单细胞技术,我们一起来看看,最新出炉的顶刊,是如何把AI与单细胞结合起来的。 另外,今天是周末,所以会有两篇文章——一篇文献速递&…...

[图解]产品经理创新之阿布思考法
0 00:00:00,000 --> 00:00:01,900 那刚才我们讲到了 1 00:00:02,730 --> 00:00:03,746 业务序列图 2 00:00:03,746 --> 00:00:04,560 然后怎么 3 00:00:05,530 --> 00:00:06,963 画现状,怎么改进 4 00:00:06,963 --> 00:00:09,012 然后改进的模式…...
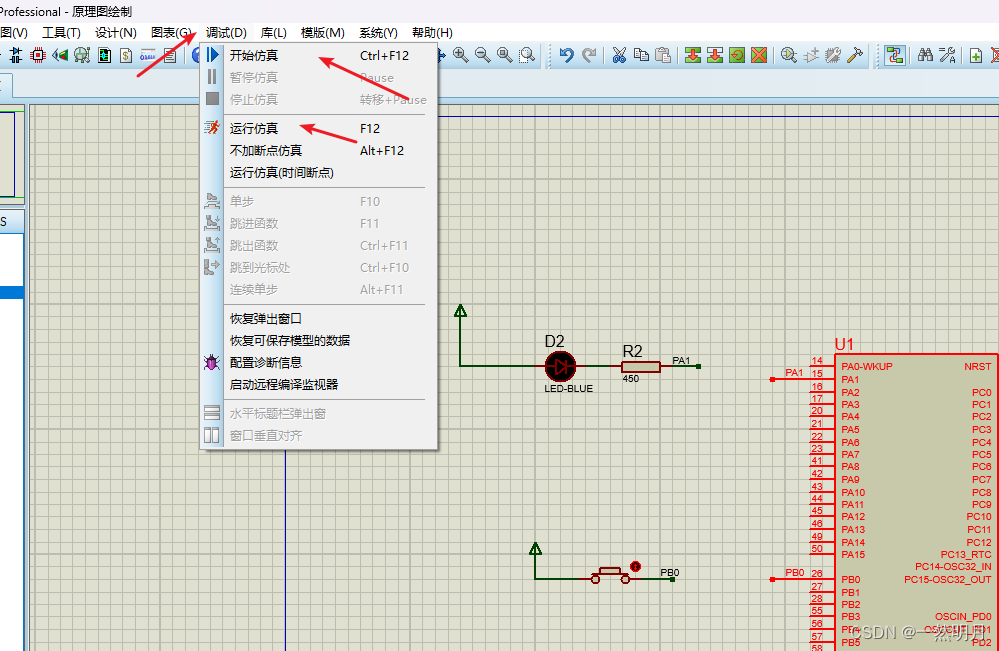
Proteus仿真小技巧(隔空连线)
用了好几天Proteus了.总结一下使用的小技巧. 目录 一.隔空连线 1.打开添加网络标号 2.输入网络标号 二.常用元件 三.运行仿真 四.总结 一.隔空连线 引出一条线,并在末尾点一下. 1.打开添加网络标号 选择添加网络标号, 也可以先点击按钮,再去选择线(注意不要点端口) 2.…...
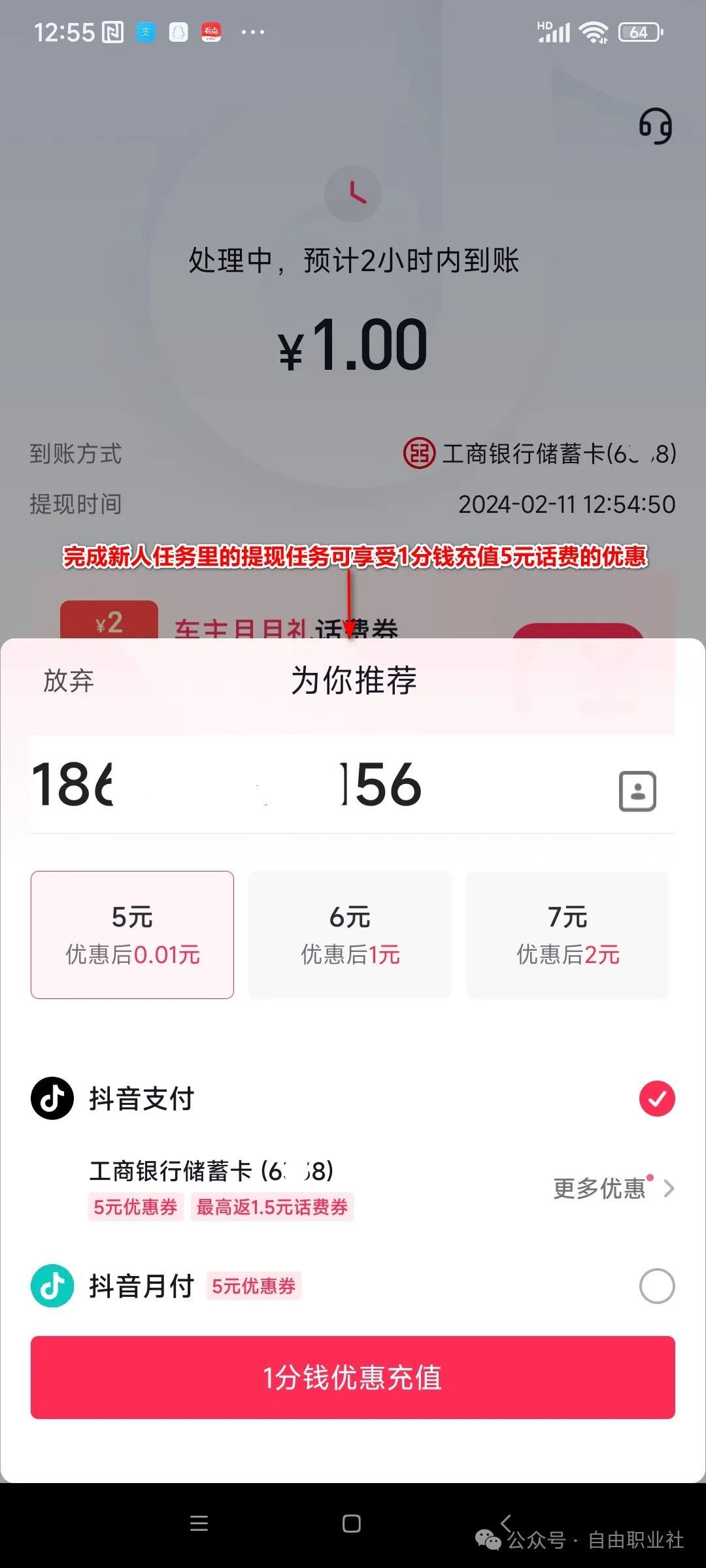
抖音极速版:抖音轻量精简版本,新人享大福利
和快手一样,抖音也有自己的极速版,可视作抖音的轻量精简版,更专注于刷视频看广告赚钱,收益比抖音要高,可玩性更佳。 抖音极速版简介 抖音极速版是一个提供短视频创业和收益任务的平台,用户可以通过观看广…...

leetCode-hot100-数组专题之双指针
数组双指针专题 1.同向双指针1.1例题26.删除有序数组中的重复项27.移除元素80.删除有序数组中的重复项 Ⅱ 2.相向双指针2.1例题11.盛最多水的容器42.接雨水581.最短无序连续子数组 双指针在算法题中很常见,下面总结双指针在数组中的一些应用,主要分为两类…...
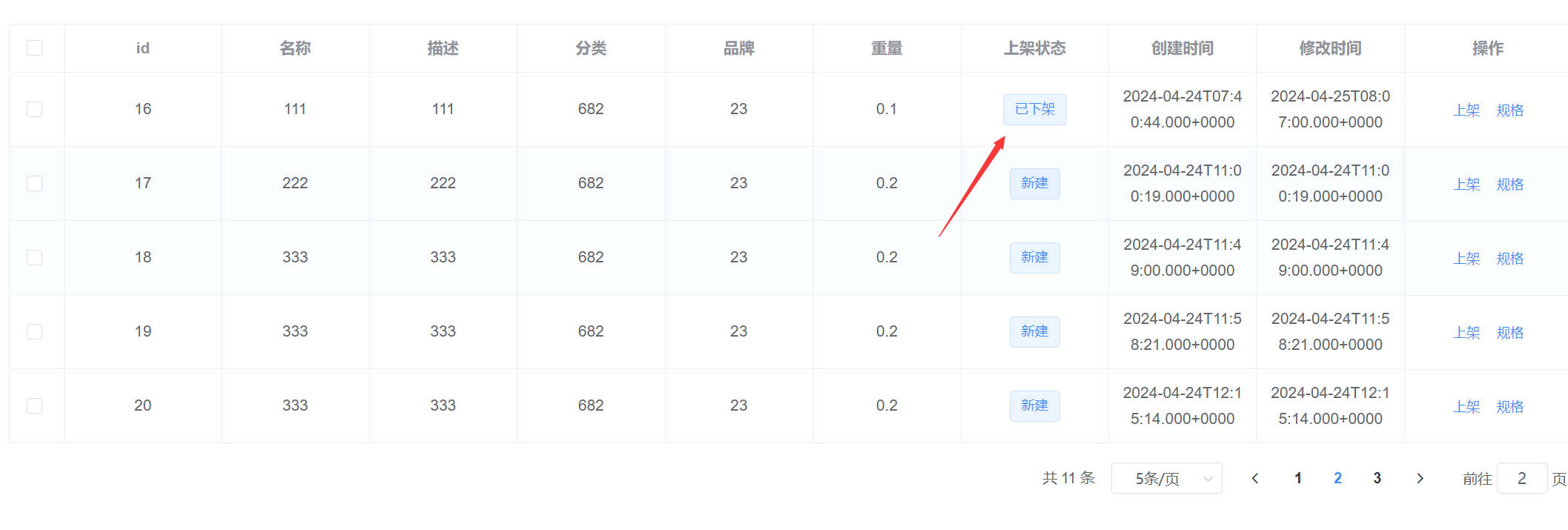
完成商品SPU管理页面
文章目录 1.引入前端界面1.将前端界面放到commodity下2.创建菜单3.进入前端项目,使用npm添加依赖1.根目录下输入2.报错 chromedriver2.27.2的问题3.点击链接下载压缩包,然后使用下面的命令安装4.再次安装 pubsub-js 成功5.在main.js中引入这个组件 4.修改…...
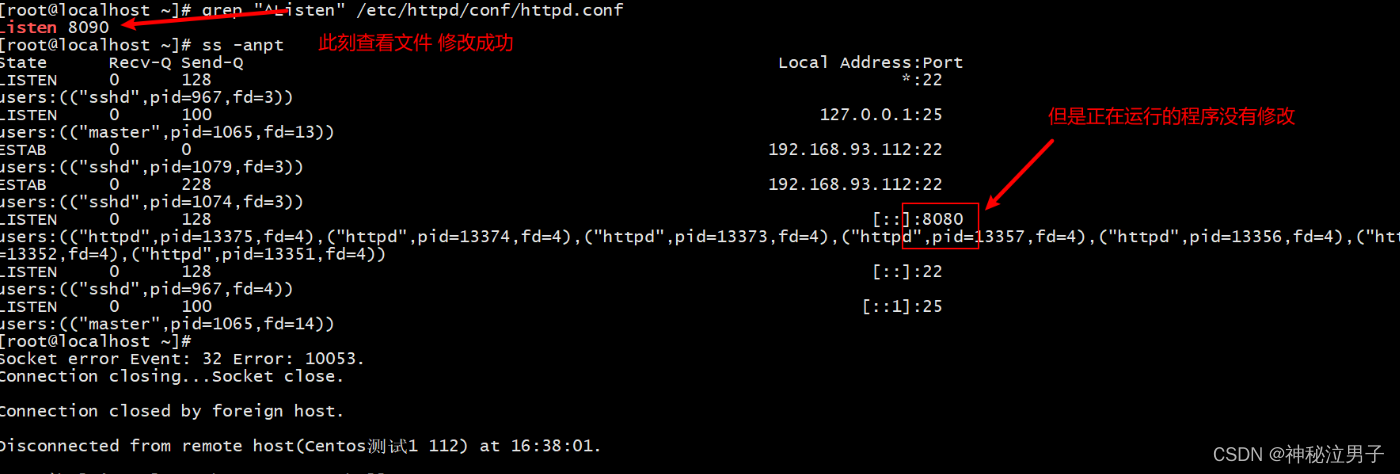
Ansible实战YAML语言完成apache的部署,配置,启动全过程
🏡作者主页:点击! 🏝️Ansible专栏:点击! ⏰️创作时间:2024年5月24日15点59分 目录 💯趣站推荐💯 🎊前言 ✨️YAML语言回顾 🎆1.编写YAML文…...

深入探索微软Edge:新一代浏览器的演进与创新
在数字时代的浪潮中,浏览器已不再只是简单的网页访问工具,而是成为了连接信息、服务与用户之间的重要桥梁。微软Edge作为微软公司推出的一款全新的浏览器,不仅承载着微软在互联网领域的最新愿景,还融合了多项前沿技术,…...

k8s使用Volcano调度gpu
k8s部署 https://www.yangxingzhen.com/9817.html cri-dockerd安装 https://zhuanlan.zhihu.com/p/632861515 安装nvidia-container-runtime https://docs.nvidia.com/datacenter/cloud-native/container-toolkit/latest/install-guide.html 安装k8s-device-plugin https://…...

x的平方根-力扣
本题想到使用二分法不断逼近一个区间,直到最后趋近于x,从而求得解。注意的点,一开始使用 if(mid * mid < x) 进行判断时,会出现越界,原因是输入一个很大的数是,超过int表示的范围,继而修改为…...
hot100 -- 回溯(上)
目录 🍞科普 🌼全排列 AC DFS 🚩子集 AC DFS 🎂电话号码的字母组合 AC DFS 🌼组合总和 AC DFS 🍞科普 忘记 dfs 的,先看看这个👇 DFS(深度优先搜索…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
