Day42 最后一块石头的重量Ⅱ + 目标和 + 一和零
1049 最后一块石头的重量Ⅱ
题目链接:1049.最后一块石头的重量Ⅱ
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
思路:本题可将原数组划分为两个总和近似的背包,二者相撞,则为最小值。因此,算出原数组的sum后,target = sum/2,于是问题转为向target包中能装的最大重量,则剩余的即为sum - dp[target],由于dp[target] <= target, target又为sum向下取整,故sum-dp[target]必大于dp[target]。
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {vector<int> dp(3001, 0);int sum = 0;for (int i = 0; i < stones.size(); i++) sum += stones[i];int target = sum / 2;for (int i = 0; i < stones.size(); i++) { // 遍历物品for (int j = target; j >= stones[i]; j--) { // 遍历背包dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - dp[target] - dp[target];}
};
494 目标和
题目链接:494.目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
思路:本题较难,建议学习代码随想录的视频。
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int i = 0; i < nums.size(); i++) sum += nums[i];if (abs(target) > sum) return 0; // 此时没有方案if ((target + sum) % 2 == 1) return 0; // 此时没有方案int bagSize = (target + sum) / 2;vector<int> dp(bagSize + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
};474 一和零
题目链接:474.一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
思路:本题仍然是01背包,但限制有两个方面,分别是0的数量和1的数量,因此使用二维dp。
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0));for (string str : strs){int oneNum = 0, zeroNum = 0;for (char c : str) {if (c == '0') zeroNum++;else oneNum++;}for (int i = m; i >= zeroNum; i--) { for (int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
};
相关文章:

Day42 最后一块石头的重量Ⅱ + 目标和 + 一和零
1049 最后一块石头的重量Ⅱ 题目链接:1049.最后一块石头的重量Ⅱ 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和…...

01.爬虫---初识网络爬虫
01.初识网络爬虫 1.什么是网络爬虫2.网络爬虫的类型3.网络爬虫的工作原理4.网络爬虫的应用场景5.网络爬虫的挑战与应对策略6.爬虫的合法性总结 1.什么是网络爬虫 网络爬虫,亦称网络蜘蛛或网络机器人,是一种能够自动地、系统地浏览和收集互联网上信息的程…...
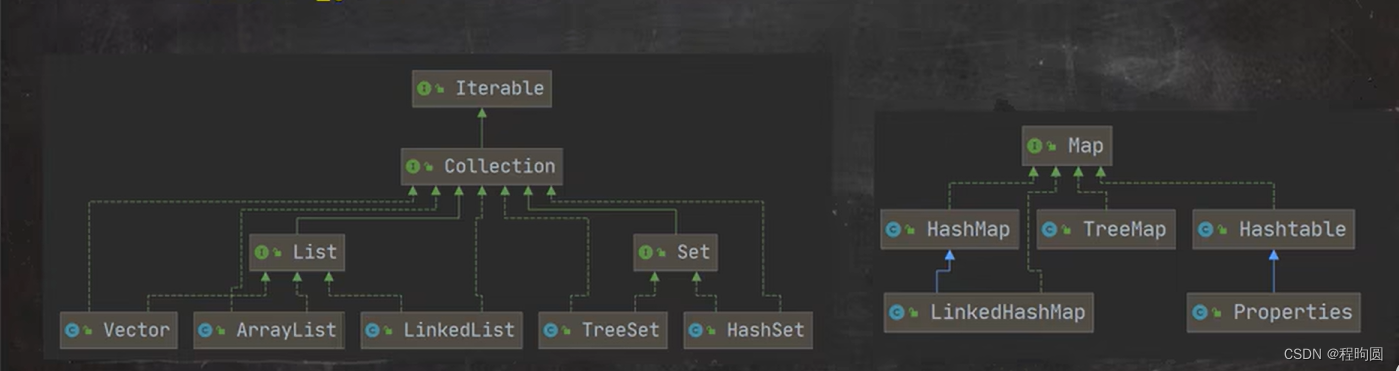
集合、Collection接口特点和常用方法
1、集合介绍 对于保存多个数据使用的是数组,那么数组有不足的地方。比如, 长度开始时必须指定,而且一旦制定,不能更改。 保存的必须为同一类型的元素。 使用数组进行增加/删除元素的示意代码,也就是比较麻烦。 为…...

12. Web开发:介绍Web开发的基本概念,Servlet和JSP的使用,MVC设计模式的应用等。
Web开发的轻松入门之旅 想象一下,Web开发就像是搭建一个在线的小家,你既是设计师,又是建筑师,还是管家。我们一步步来探索这个过程,保证简单易懂,就像搭积木一样有趣! Web开发基础认知 Web开…...

文件系统--inode
文章目录 概述认识磁盘了解磁盘的存储结构对磁盘的存储结构进行逻辑抽象 操作系统对磁盘的使用宏观认识细节认识再谈目录再谈文件的增删 概述 文件有很多,但是被打开的文件很少,这些没有被打开的文件在磁盘中,这就叫做磁盘文件。每次先打开一…...
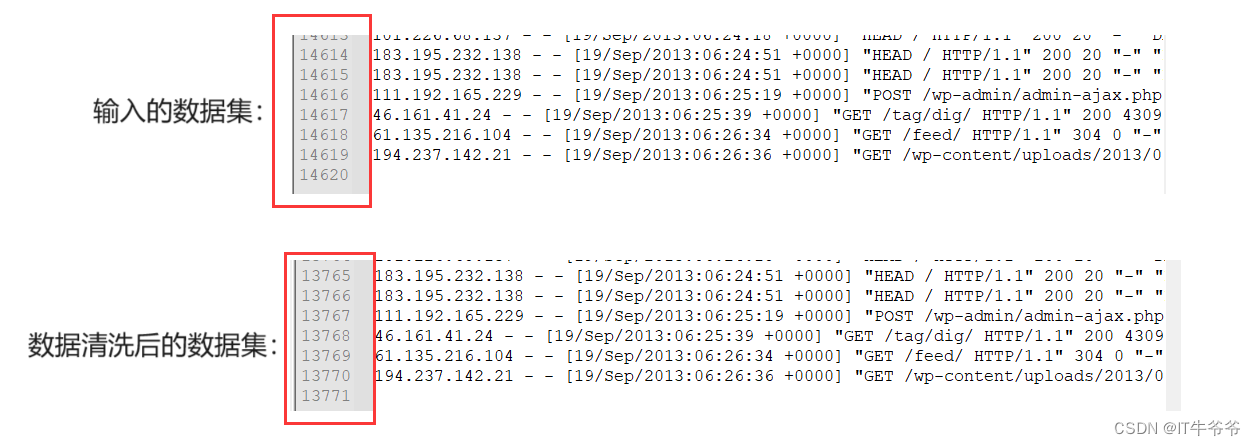
数据清洗(ETL)案例实操
文章目录 数据清洗(ETL)概述案例需求和分析代码实现和结果分析 数据清洗(ETL)概述 “ETL,是英文Extract-Transform-Load的缩写,用来描述将数据从来源端经过抽取(Extract)、转换&…...
)
Zookeeper 面试题(一)
1. ZooKeeper 适合哪些应用场景? ZooKeeper 是一个高性能、高可靠的分布式协调系统,它在分布式系统和大数据领域中有着广泛的应用。以下是 ZooKeeper 适合的一些应用场景: 数据发布/订阅:ZooKeeper 可以作为配置中心,…...

怎么安装django特定版本
要安装Django的特定版本,你可以使用Python的包管理工具pip。以下是在命令行中安装Django特定版本的步骤: 确保你的计算机上已经安装了Python和pip。如果没有安装,你可以从Python官方网站下载并安装最新版本的Python,pip通常会随Py…...

关于Broken pipe异常的一点学习记录
什么是Broken pipe? pipe,管道,管道里面自然就是数据,通过指从文件或网络套接字读取的数据。当一个进程试图向一个已关闭的管道(pipe)写数据或者从一个已关闭的通道读数据时就会出现中断,也就是Broken pi…...

第十一课,end关键字、简单while循环嵌套、初识for循环
一,end关键字 end关键字用于在print输出的内容后面声明结束的字符,我们之前学过并且十分了解print是默认输出内容之后跟着换行的,如果我们不希望换行而希望使用其它字符来代替换行,就可以用end关键字来实现 特殊的,en…...

spring boot 集成mongodb
引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-mongodb</artifactId><version>2.2.0.RELEASE</version></dependency>配置db: spring:data:mongodb:host: 127.0.…...

从零开始搭建SpringCloud Alibaba微服务架构
Spring Cloud Alibaba是Spring Cloud的一个拓展项目,它用于构建基于阿里巴巴的微服务应用。它提供了多个阿里巴巴的开源组件,如Nacos、Sentinel、Dubbo等,用于解决微服务架构中的服务注册、配置管理、流量控制等问题。 Spring Cloud Alibaba…...
之JdbcTemplate)
SpringBoot(八)之JdbcTemplate
SpringBoot(八)之JdbcTemplate 文章目录 SpringBoot(八)之JdbcTemplate1.添加依赖项:2. 配置数据库连接3.创建表信息4. 创建数据模型5. 创建 Repository6.测试,创建TestController spring-boot-starter-jdbc 是 Spring…...

ClickHouse 24.4 版本发布说明
本文字数:13148;估计阅读时间:33 分钟 审校:庄晓东(魏庄) 本文在公众号【ClickHouseInc】首发 新的一个月意味着新版本的发布! 发布概要 本次ClickHouse 24.4版本包含了13个新功能🎁…...

amtlib.dll打不开怎么办?一键修复丢失amtlib.dll方法
电脑丢失amtlib.dll文件是什么情况?出现amtlib.dll打不开怎么办?这样的情况有什么解决方法呢?今天就和大家聊聊amtlib.dll文件同时教大家一键修复丢失amtlib.dll方法?一起来看看amtlib.dll文件丢失会有哪些方法修复? a…...

【退役之重学Java】关于 volatile 关键字
一、是什么 volatile 是Java中的关键字,用于声明变量,具有两个主要特性使其特殊。 二、两个特性 首先,如果有一个volatile变量,任何线程都无法将其缓存在计算机的缓存中。访问始终从主内存中进行。其次,如果volatile变…...
“大数据建模、分析、挖掘技术应用研修班”的通知!
随着2015年9月国务院发布了《关于印发促进大数据发展行动纲要的通知》,各类型数据呈现出了指数级增长,数据成了每个组织的命脉。今天所产生的数据比过去几年所产生的数据大好几个数量级,企业有了能够轻松访问和分析数据以提高性能的新机会&am…...

Uniapp自定义默认返回按钮回退页面
//自定义后退时的操作onBackPress() {this.back1();return true;}, methods: { //跳转到 tabBar 页面,并关闭其他所有非 tabBar 页面back1() {uni.switchTab({url: /pages/mangement/mangement});},//关闭所有页面,打开到应用内的某个页面。back1() {uni…...
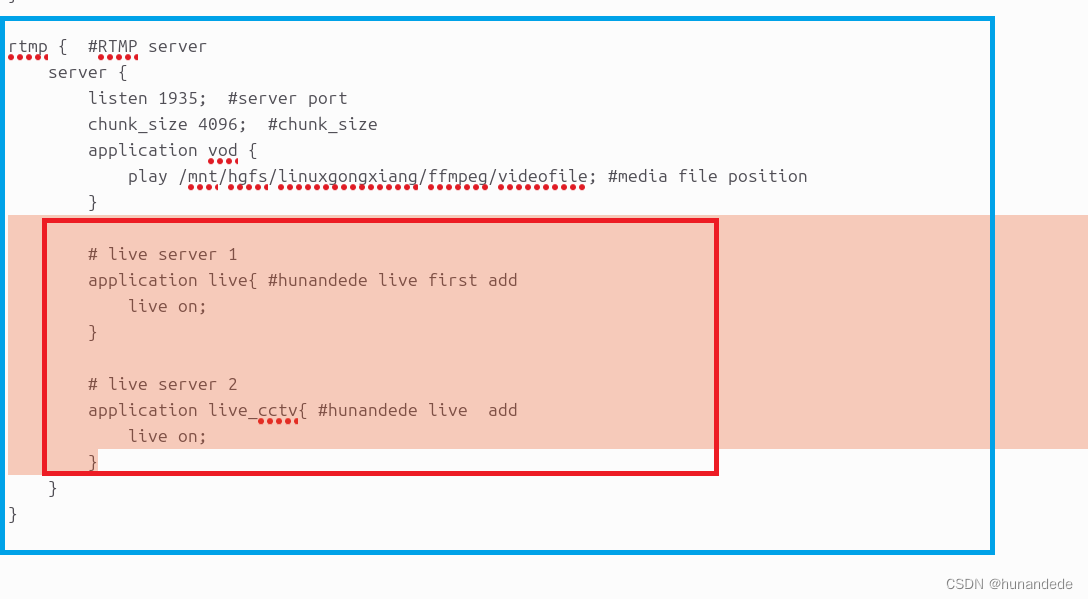
音视频开发5 补充 - Nginx搭建rtmp流媒体服务器,目的是让ffmpeg 可以直播推流
直播推流 ffmpeg -re -i out.mp4 -c copy flv rtmp://server/live/streamName -re, 表示按时间戳读取文件 参考: Nginx 搭建 rtmp 流媒体服务器 (Ubuntu 16.04) https://www.jianshu.com/p/16741e363a77 第一步 准备工作 安装nginx需要的依赖包 打开 ubutun 终端…...

小猫咪的奇幻冒险:一个简单的Python小游戏
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、游戏简介与演示 二、游戏开发与运行 1. 环境搭建 2. 代码解析 3. 加速机制 三、游戏…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
