Redis实现MQ
MQ的提出
上游发出请求后阻塞等待下游给到反馈,否则整个流程将一直阻塞。
提出mq之后:即有producer mq consumer 三者
MQ的特点
异步解耦
在有了 mq 后,producer 不需要过分关心 consumer 的身份信息,只需要把消息按照指定的协议投递到对应的 topic 即可
producer 在处理请求时,只需要把消息投递到 mq 即可认为流程处理结束,相比于同步请求下游,整个流程会更加轻便灵活,拥有更高的吞吐量
流量削峰
因为有 mq 作为缓冲层. 下游 consumer 可以设定好合适的消费限流参数,按照指定的速率进行消费,能够在很大程度上对 consumer 起到保护作用
Redis自身的缺点(无论是做缓存还是做mq都存在的)
价格昂贵:redis本身是基于内存的,相比传统的mq组件是基于磁盘的。因此总容量可能有限。
存在数据丢失:即使有RDB/AOF的持久化策略,也难免存在数据丢失的问题,因为这个持久化是异步执行的,只要是异步,都不能说它是百分百的。
Redis自身的优点:
轻量,部署方便,运维成本低。
基于List实现的消息队列
首先,在使用 list 充当消息队列时,list 对应的 key 则对应为消息的 topic 名称.
producer 在投递消息时,可以使用 lpush 指令
consumer 消费消息时,使用 rpop 指令
但是存在一定的缺陷:
首先,consumer 在消费时,一定是一个类似于 loop thread 的自旋模型,每一轮循环中,通过 rpop 指令尝试从 list 中读取消息,如果成功读取到了消息,则进行相应的逻辑处理.
然而在此处,redis 的 rpop 指令是非阻塞型的,即在 list 没有数据时,也会即时返回一个结果为 nil 的响应,这样在自旋模型下,对CPU是一笔不小的损耗。
倘若我们在 rpop 捕捉到 nil 时,立即开启下一轮循环,则这个轮询行为可能是没有意义的,因为 list 中可能仍然不存在数据. 这样的高频率自旋,对于 cpu 资源是一种无谓的损耗
倘若我们选择让 consumer 休眠一段时间进行循环,这个休眠的时长又具有一定的人为误判性. 倘若我们把时长设得太短,仍然会存在 cpu 浪费的问题;倘若设得太长,则可能会导致消息处理不及时的问题
在这个过程中,最理想的实现方案是,在 list 中有数据到达时,我们令 consumer 即时获取到对应的结果;倘若 list 数据为空,则令 consumer 陷入阻塞等待的状态,直到有数据抵达时程序才被唤醒.
推出阻塞等待机制:
BRPop key 【阻塞等待的超时时长】
达到此阈值仍未获取数据时会返回 nil. 如果设置为 0 ,则代表没有这个超时限制.
基于Pub/Sub
相关文章:

Redis实现MQ
MQ的提出 上游发出请求后阻塞等待下游给到反馈,否则整个流程将一直阻塞。 提出mq之后:即有producer mq consumer 三者 MQ的特点 异步解耦 在有了 mq 后,producer 不需要过分关心 consumer 的身份信息,只需要把消息按照指定的协议…...

【Linux】进程终止与进程等待
目录 进程终止 errno exit和_exit 进程等待 wait和waitpid 宏:WIFEXITED 非阻塞等待 进程终止 下面要谈的一个话题就是进程终止,就是说一个进程退出了,可能有三种情况 1.进程代码执行完,结果是正确的 2.进程代码执行完&…...

数据结构_链式二叉树(Chained binary tree)基础
✨✨所属专栏:数据结构✨✨ ✨✨作者主页:嶔某✨✨ 二叉树的遍历 前序、中序以及后序遍历 学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的结点进行相应的操作ÿ…...

python梯度下降法求解三元线性回归系数,并绘制结果
import numpy as np import matplotlib.pyplot as plt # 生成随机数据 np.random.seed(0) X1 2 * np.random.rand(100, 1) X2 3 * np.random.rand(100, 1) X3 4 * np.random.rand(100, 1) y 4 3 * X1 5 * X2 2 * X3 np.random.randn(100, 1) # 合并特征 X_b np.hsta…...

Linux基础(五):常用基本命令
从本节开始,我们正式进入Linux的学习,通过前面的了解,我们知道我们要以命令的形式使用操作系统(使用操作系统提供的各类命令,以获得字符反馈的形式去使用操作系统。),因此,我们是很有…...

原始字面常量(C++11)
原始字面常量(C11) 文章目录 原始字面常量(C11)前言一、原始字面量二、代码示例总结 前言 字面量一般是指数值(12、454等)和字符串(“Hw”、“h\t”),但是有时候我们想表…...
|设计模式的六大原则)
C++|设计模式(〇)|设计模式的六大原则
这里文章只做简要描述,作为扫盲 在软件开发过程中,遵循一定的设计原则可以帮助开发者创建更加灵活、可维护和可扩展的系统。设计模式的六大原则是面向对象设计的核心理念,本文将详细介绍这些原则,并结合实例说明它们的重要性和应用…...
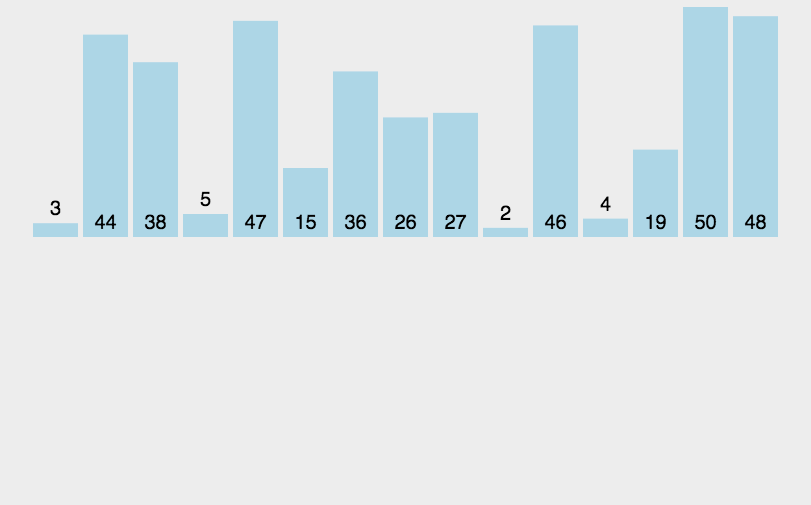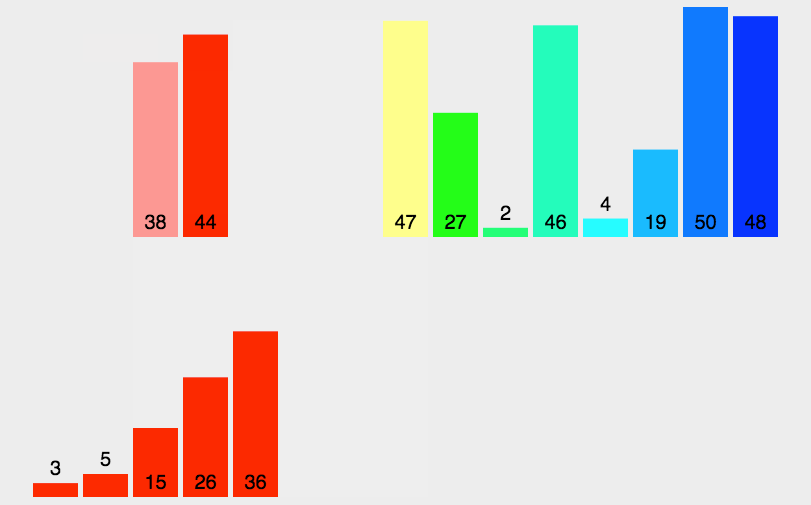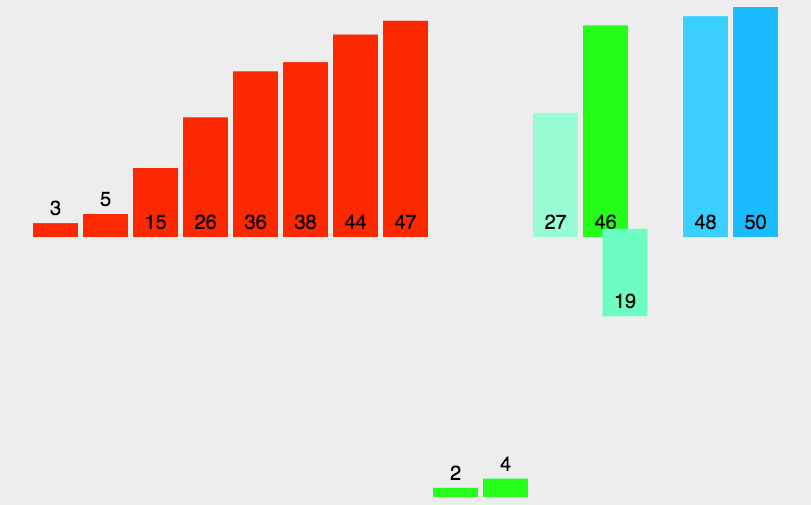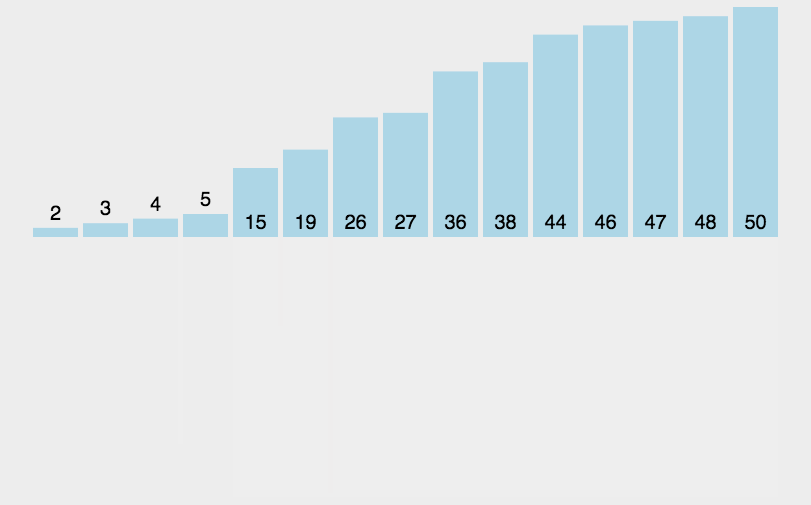
【排序算法】——归并排序(递归与非递归)含动图
制作不易,三连支持一下吧!!! 文章目录 前言一.归并排序递归方法实现二.归并排序非递归方法实现 前言 这篇博客我们将介绍归并排序的原理和实现过程。 一、归并排序递归方法实现 基本思想: 归并排序(MERGE-…...

Mysql自增id、uuid、雪花算法id的比较
MySQL自增id: 优点: 1.简单易用 MySQL自增id 由数据库自动生成。 2.效率高 自增id是按顺序递增的,可以提高插入和查询的效率。 3.索引效率高 自增id可以作为主键或索引列,提高查询效率。 缺点: 1.不适用于分布式系统 在分布式…...

【会议征稿,IEEE出版】第九届信息科学、计算机技术与交通运输国际学术会议(ISCTT 2024,6月28-30)
第九届信息科学、计算机技术与交通运输国际学术会议(ISCTT 2024)将于2024年6月28-30日在中国绵阳举行。 ISCTT 2024将围绕 “信息科学”、"计算机技术”、“交通运输” 等最新研究领域,为来自国内外高等院校、科学研究所、企事业单位的专…...

二十八篇:嵌入式系统实战指南:案例研究与未来挑战
嵌入式系统实战指南:案例研究与未来挑战 1. 引言 1.1 嵌入式系统的重要性及其应用广度 在当今快速发展的技术领域中,嵌入式系统扮演着至关重要的角色。这些系统是专门设计的计算机硬件和软件的组合,旨在执行特定任务,如控制、监…...

探索编程乐趣:绘制螺旋图的奇幻之旅
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一、引言:编程的魔法世界 二、绘制螺旋图的准备工作 三、代码实战:…...

C# 语法糖
语法糖 var关键字(隐式类型变量):自动属性:简化的事件访问器:Lambda表达式和匿名方法:扩展方法:LINQ查询:异步编程(async和await):嵌套匿名类型&a…...

ubuntu 安装VMtool 实现复制粘贴
如果只是安装一个根本没有用,而是两个命令都要安装 sudo apt-get install open-vm-tools sudo apt-get install open-vm-tools-desktop引用博客...
智慧仓储新动力:EasyCVR+AI视频智能监管系统方案助力仓储安全高效管理
一、背景 随着物流行业的快速发展和智能化水平的提升,智慧仓储视频智能监管系统已成为现代仓储管理的重要组成部分。本系统通过综合运用物联网、视频分析、边缘计算等技术手段,实现对仓储环境的全面监控、智能分析和高效管理。 TSINGSEE青犀视频汇聚Ea…...
)
gcc源码分析(AST抽象语法树)
文章目录 三、AST相关1、AST(抽象语法树)1.1 树结点的声明1.2 树结点的结构1.2.1 tree_node联合体1.2.2 tree_base结构体1.2.3 tree_common结构体1.2.4 常量结构体1.2.5 **标识符节点**2、符号绑定,作用域与block树节点2.1 lang_identifier结构体2.2 c_binding结构体2.3 scop…...
ES基础概念
本文不介绍如何使用ES(使用ES见:) 1.ES生态圈 ES: Logstash:数据处理服务程序,解析转换加工数据; Kibana:数据展示、集群管理,数据可视化、ES管理与监控、报表等…...

断更是我的错
打算在暑假每天两个文章,大概是6月20多号开始吧。...

红队攻防渗透技术实战流程:云安全之云原生安全:云堡垒机
红队云攻防实战 1. 云原生安全-防护设备-云堡垒机1. 云原生安全-防护设备-云堡垒机 堡垒机攻防:(意义) https://mp.weixin.qq.com/s/-WcgyVoTCZuPamVtI5MrJw 堡垒机漏洞:(已知)https://avd.aliyun.com/search?q=%E5%A0%A1%E5%9E%92%E6%9C%BA 云堡垒机:(云攻防) http…...

Down with typename
1. 隐式类型名的详情 C20 之前,typename 在一些其他情况下是不必要的: • 指定继承类的基类型时 • 在构造函数中将初始值传递给基类时 • 在类声明中使用类型成员时 #include <iostream> struct Impl {Impl(){ std::cout << "Impl ctor" &…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
