【C++进阶】AVL树
0.前言
前面我们已经学习过二叉搜索树了,但如果我们是用二叉搜索树来封装map和set等关联式容器是有缺陷的,很可能会退化为单分支的情况,那样效率就极低了,那么有没有方法来弥补二叉搜索树的缺陷呢?
那么AVL树就出现了,通过AVL树的右单旋、左单旋、左右单旋,右左单旋等操作来防止二叉搜索树退化为单分支的情况出现。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
AVL树也是以这两位大佬名字的首字母来命名的。
1.AVL树的概念
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树是AVL树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
我们这里使用的平衡因子是右子树高度 - 左子树高度。

2.AVL树节点的定义
代码如下:
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left; //该节点的左孩子AVLTreeNode<K, V>* _right; //该节点的右孩子AVLTreeNode<K, V>* _parent; //该节点的双亲pair<K, V> _kv; //该节点的key和valueint _bf; //balance factor 平衡因子AVLTreeNode(const pair<K, V>& kv) //该节点初始化:_left(nullptr) , _right(nullptr), _parent(nullptr), _kv(kv) , _bf(0){}
};3.AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么
AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
插入思路:
1.按照搜索树规则插入
2.更新插入节点的祖先节点的平衡因子
a.插入父亲的右边,父亲的平衡因子--
b.插入父亲的左边,父亲的平衡因子++
c.父亲平衡因子 == 0, 父亲所在子树高度不变,不再继续往上更新。插入结束
d.父亲平衡因子 == 1 or -1, 父亲所在子树高度变了,继续往上更新。
e.父亲平衡因子 == 2 or -2, 父亲所在子树已经不平衡了,需要旋转处理。
更新中不可能出现其他值,插入之前树是AVL树,平衡因子要么是1 -1 0, ++ --
最多就是c/d/e三种情况。
代码如下:
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){//更新结束break;}else if (parent->_bf == -1 || parent->_bf == 1){//继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){//当前子树出现了问题,需要旋转平衡一下if (parent->_bf == -2 && cur->_bf == -1){//右单旋RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){//左单旋RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右双旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左双旋//RotateRL(parent);}break;}else{//理论上不会出现这种情况,但仍要判断,大佬都不能保证自己的代码没有bugassert(false);}}return true;}4.AVL树的旋转
4.1 右单旋
插入新节点要插入较高左子树的左侧(左左)-》右单旋
图形解析:
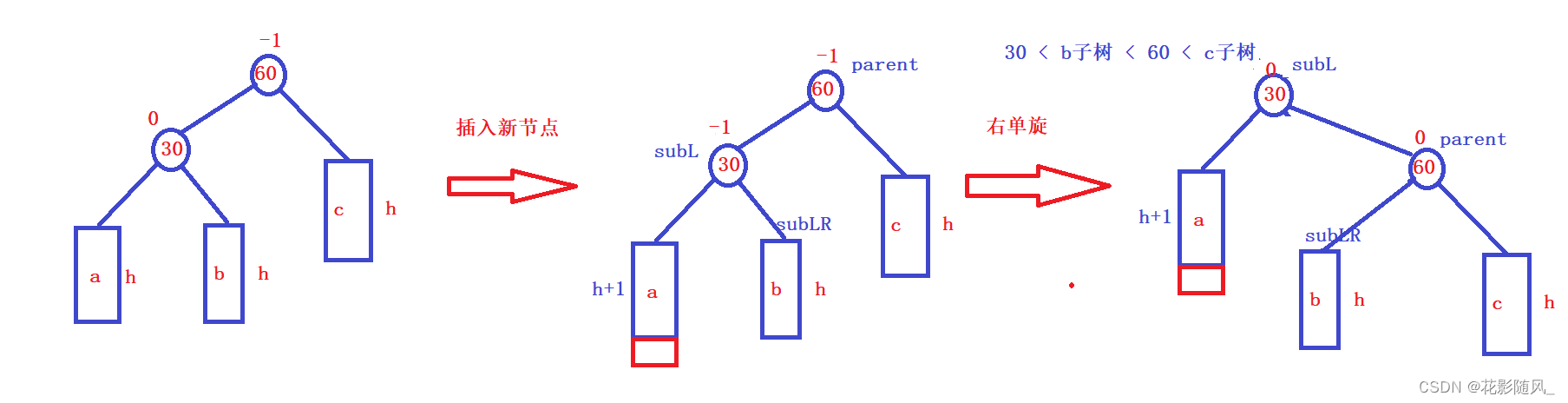
实现代码如下:
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) //subLR有可能为空,不为空时才能调整subLR的父节点subLR->_parent = parent;subL->_right = parent;//parent不一定就是根节点,也可能是子树,所以要设置一个ppNode来标记parent的父节点Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}4.2 左单旋
插入新节点要插入较高右子树的右侧(右右)-》左单旋
图形解析:
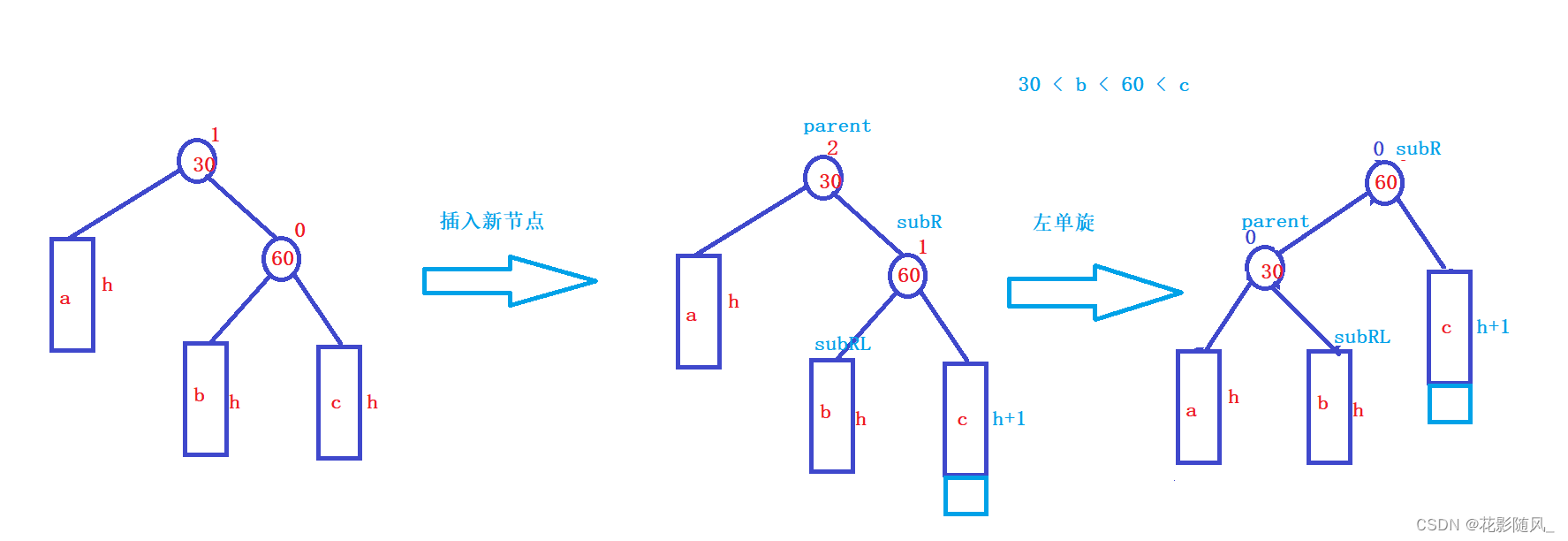
代码如下:
void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) //subRL有可能为空,不为空时才能调整subRL的父节点subRL->_parent = parent;subR->_left = parent;//parent不一定就是根节点,也可能是子树,所以要设置一个ppNode来标记parent的父节点Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}subR->_bf = parent->_bf = 0;}4.3 左右双旋
插入新节点要插入较高左子树的右侧(左右)-》左右双旋
图形解析:
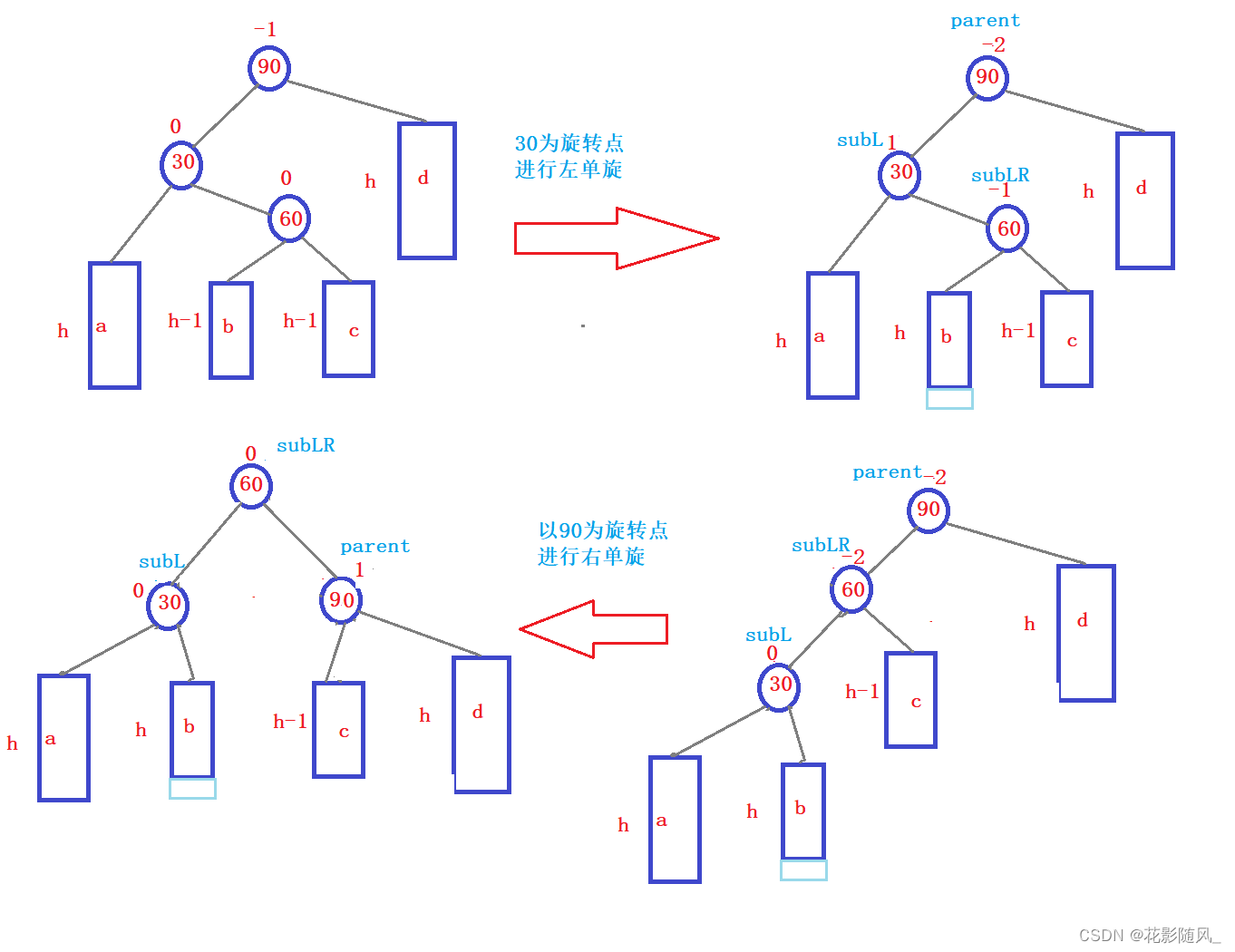
对于插入的位置根据h的高度和插入的位置时的平衡因子出现的最终的结果可分为三种情况:
1.h == 0
60自己就是新增节点。bf == 0
此时的平衡因子为,30 60 90节点都为0。
2.h > 0
a.新增节点插入的是60的左子树中 bf == -1
此时的平衡因子为,30节点为0,90为0,60为1
b.新增节点插入的是60的右子树中bf == 1
此时的平衡因子为,30节点为-1,90为0,60为0
代码如下:
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{//理论上不会出现的情况assert(false);}}4.4 右左双旋
插入新节点要插入较高右子树的左侧(右左)-》右左双旋
与左右双旋类似
代码如下:
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 0;}else if (bf == -1){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}else if (bf == 1){parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else{//理论上不会出现的情况assert(false);}}
总结:
假如以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑
1. pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR
当pSubR的平衡因子为1时,执行左单旋
当pSubR的平衡因子为-1时,执行右左双旋
2. pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL
当pSubL的平衡因子为-1是,执行右单旋
当pSubL的平衡因子为1时,执行左右双旋
旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
5.AVL树的验证
5.1 验证其是否为二叉搜索树
给一个序列进行一次中序遍历,看是否有序,有序即为二叉搜索树。
void TestAVLTree1()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };AVLTree<int, int> t1;for (auto e : a){t1.Insert({ e,e });}t1.InOrder();
}5.2 验证其是否为平衡树
bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);//不平衡if (abs(leftHeight - rightHeight) >= 2){cout << root->_kv.first << endl;return false;}//顺便检查一下平衡因子是否正确if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << endl;return false;}return _IsBalance(root->_left)&& _IsBalance(root->right);}6.AVL树的删除(了解)
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
7.AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即logN。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
8.AVL树的整体模拟代码实现
#pragma once
#include<iostream>
using namespace std;
#include<assert.h>template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left; //该节点的左孩子AVLTreeNode<K, V>* _right; //该节点的右孩子AVLTreeNode<K, V>* _parent; //该节点的双亲pair<K, V> _kv; //该节点的key和valueint _bf; //balance factor 平衡因子AVLTreeNode(const pair<K, V>& kv) //该节点初始化:_left(nullptr) , _right(nullptr), _parent(nullptr), _kv(kv) , _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){//更新结束break;}else if (parent->_bf == -1 || parent->_bf == 1){//继续往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){//当前子树出现了问题,需要旋转平衡一下if (parent->_bf == -2 && cur->_bf == -1){//右单旋RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){//左单旋RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右双旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左双旋RotateRL(parent);}break;}else{//理论上不会出现这种情况,但仍要判断,大佬都不能保证自己的代码没有bugassert(false);}}return true;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) //subLR有可能为空,不为空时才能调整subLR的父节点subLR->_parent = parent;subL->_right = parent;//parent不一定就是根节点,也可能是子树,所以要设置一个ppNode来标记parent的父节点Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) //subRL有可能为空,不为空时才能调整subRL的父节点subRL->_parent = parent;subR->_left = parent;//parent不一定就是根节点,也可能是子树,所以要设置一个ppNode来标记parent的父节点Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}subR->_bf = parent->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{//理论上不会出现的情况assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 0;}else if (bf == -1){parent->_bf = 0;subRL->_bf = 0;subR->_bf = 1;}else if (bf == 1){parent->_bf = -1;subRL->_bf = 0;subR->_bf = 0;}else{//理论上不会出现的情况assert(false);}}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}bool IsBalance(){return _IsBalance(_root);}int Height(){return _Height(_root);}int Size(){return _Size(_root);}
private:int _Size(Node* root){return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr){return 0;}return max(_Height(root->_left), _Height(root->_right)) + 1;}bool _IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);//不平衡if (abs(leftHeight - rightHeight) >= 2){cout << root->_kv.first << endl;return false;}//顺便检查一下平衡因子是否正确if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << endl;return false;}return _IsBalance(root->_left)&& _IsBalance(root->_right);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}Node* _root = nullptr;
};void TestAVLTree1()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };AVLTree<int, int> t1;for (auto e : a){t1.Insert({ e,e });}t1.InOrder();
}
void TestAVLTree2()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };AVLTree<int, int> t1;for (auto e : a){t1.Insert({ e,e });}t1.InOrder();cout << t1.IsBalance() << endl;
}相关文章:

【C++进阶】AVL树
0.前言 前面我们已经学习过二叉搜索树了,但如果我们是用二叉搜索树来封装map和set等关联式容器是有缺陷的,很可能会退化为单分支的情况,那样效率就极低了,那么有没有方法来弥补二叉搜索树的缺陷呢? 那么AVL树就出现了&…...
云部署最简单python web
最近在玩云主机,考虑将简单的web应用装上去,通过广域网访问一下,代码很简单,所以新手几乎不会碰到什么问题。 from flask import Flaskapp Flask(__name__)app.route(/) def hello_world():return Hello, World!app.route(/gree…...
【Pytorch】【MacOS】14.m1芯片使用mps进行深度模型训练
读者要先自行安装python以及anaconda,并且配置pytorch环境 第一步 测试环境 import torch # 判断macOS的版本是否支持 print(torch.backends.mps.is_available()) # 判断mps是否可用 print(torch.backends.mps.is_built())如果第一个语句为False,说明当前…...
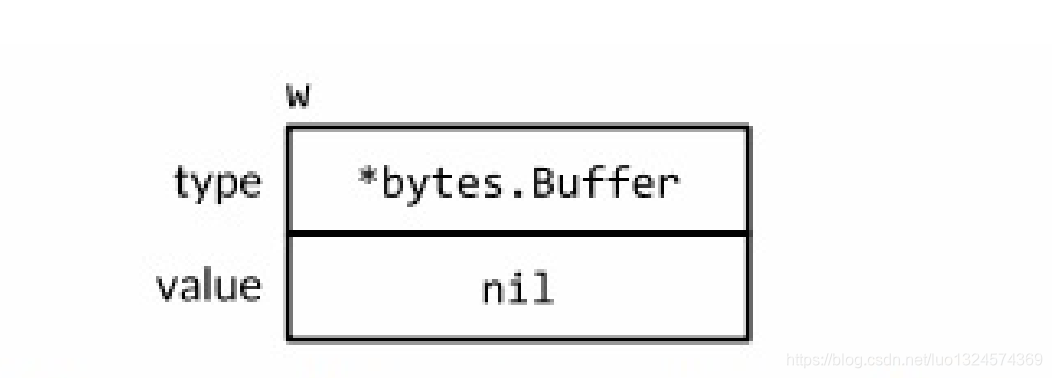
go学习笔记-从圣经中抄录的接口值的思考
接口值 接口值,由两个部分组成,一个具体的类型和那个类型的值 下面4个语句中,变量w得到了3个不同的值。( 开始和最后的值是相同的) var w io.Writer w os.Stdout w new(bytes.Buffer) w nil var w io.Writer var…...

ICML 2024 时空数据(Spatial-Temporal)论文总结
2024ICML(International Conference on Machine Learning,国际机器学习会议)在2024年7月21日-27日在奥地利维也纳举行 (好像ICLR24现在正在维也纳开)。 本文总结了ICML 24有关时空数据(Spatial-temporal) 的相关论文…...

多线程(C++11)
多线程(C) 文章目录 多线程(C)前言一、std::thread类1.线程的创建1.1构造函数1.2代码演示 2.公共成员函数2.1 get_id()2.2 join()2.3 detach()2.4 joinable()2.5 operator 3.静态函数4.类的成员函数作为子线程的任务函数 二、call…...
HLS入门
目录 一、 内容介绍二、 理解HLS2.1 HLS是什么?与VHDL/Verilog编程技术有什么关系?2.2 HLS有哪些关键技术问题?目前存在什么技术局限性? 三、 HLS在Quartus上的实现3.1 配置环境3.2 测试 四、 参考链接 一、 内容介绍 理解HLSHLS在Quartus上…...
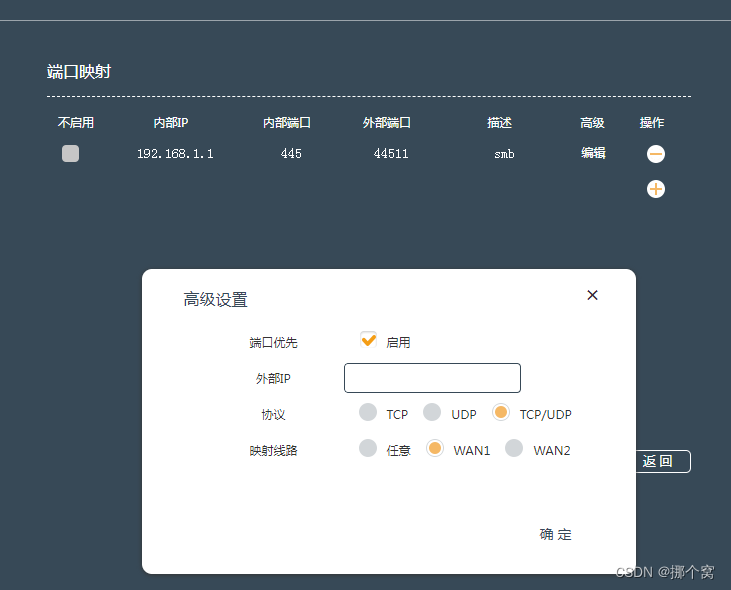
电信光猫的USB存储对外网开放访问
前提条件当然是要有公网IP地址了,没有的话去找电信索要,然后可以使用动态域名正常访问。 我的电信光猫发现共享访问速度还可以,会有31M/s左右的写入速度 但是有一个不方便的是,无法从外网提供访问,SMB协议所用的445端…...

世界上首位AI程序员诞生,AI将成为人类的对手吗?
3月13日,世界上第一位AI程序员Devin诞生,不仅能自主学习新技术,自己改Bug,甚至还能训练和微调自己的AI模型,表现已然远超GPT-4等“顶流选手”。 AI的学习速度如此之快,人类的教育能否跟上“机器学习”的速…...
什么是创造力?如何判断自己的创造力?
创造力,主要表现为创新思想、发现和创造新事物的能力,是知识,智力和能力的综合能力,尤其是在职业发展方面,创造力具有重要的意义,企业的核心竞争力就来源于创造力,这就需要具有创造力的员工来推…...
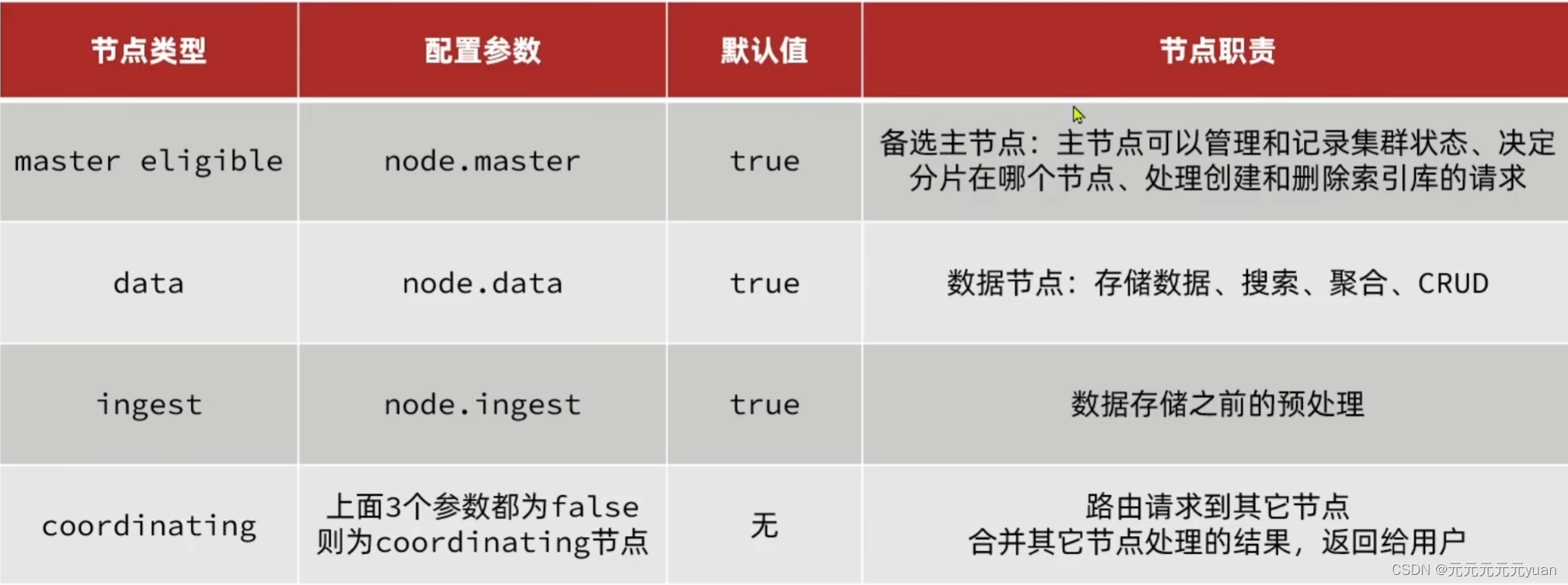
Elasticsearch集群搭建学习
Elasticsearch集群聚合、集群搭建 RestClient查询所有高亮算分控制 数据聚合DSL实现Bucket聚合DSL实现Metrics聚合RestAPI实现聚合 拼音分词器如何使用拼音分词器?如何自定义分词器?拼音分词器注意事项? 自动补全数据同步集群搭建ES集群结构创…...

数据库(vb.net+OleDB+Access)简易学生信息管理系统
在我们日常生活当中,数据库一词往往离不开我们的编程界,在学校、仓库等方面起着存储数据及数据关系作用的文件。相较于Excel,Access可以存储无限多的记录,内容也十分丰富,例如文本、数字、日期、T&F等。而且不需要…...

Android 自定义图片进度条
用系统的Progressbar,设置图片drawable作为进度条会出现图片长度不好控制,容易被截断,或者变形的问题。而我有个需求,使用图片背景,和图片进度,而且在进度条头部有个闪光点效果。 如下图: 找了…...

对话:用言语构建深刻的思想碰撞
对话:用言语构建深刻的思想碰撞 在写书中,对话是一种有力的工具,能与读者进行有效的沟通和交流,引发深思和反思。它不仅是信息传递的方式,更是加深情感、探讨主题和吸引读者参与的桥梁。你应从读者的角度思考…...
)
Linux完整版命令大全(九)
4. linux压缩备份命令 ar 功能说明:建立或修改备存文件,或是从备存文件中抽取文件。语 法:ar[-dmpqrtx][cfosSuvV][a<成员文件>][b<成员文件>][i<成员文件>][备存文件][成员文件]补充说明:ar可让您集合许多…...

solidworks画螺栓学习笔记
螺栓 单位mm 六边形 直径16mm 水平约束 拉伸 选择厚度6mm 拉伸切除 画相切圆 切除厚度6mm,反向切除 ,拔模角度45 螺栓 直径9mm,长度30mm 倒角 直径1mm,角度45 异形孔向导 螺纹线 偏移打勾,距离为2mm&#…...

【Spark】加大hive表在HDFS存的每个文件的大小
配置参数: spark.hadoop.hive.exec.orc.default.stripe.size78643200 spark.hadoop.orc.stripe.size78643200 spark.hadoopRDD.targetBytesInPartition78643200 spark.hadoop.hive.exec.dynamic.partition.modenonstrict spark.sql.sources.partitionOverwriteMode…...

2024 年 5 个 GO REST API 框架
什么是API? API是一个软件解决方案,作为中介,使两个应用程序能够相互交互。以下一些特征让API变得更加有用和有价值: 遵守REST和HTTP等易于访问、广泛理解和开发人员友好的标准。API不仅仅是几行代码;这些是为移动开…...
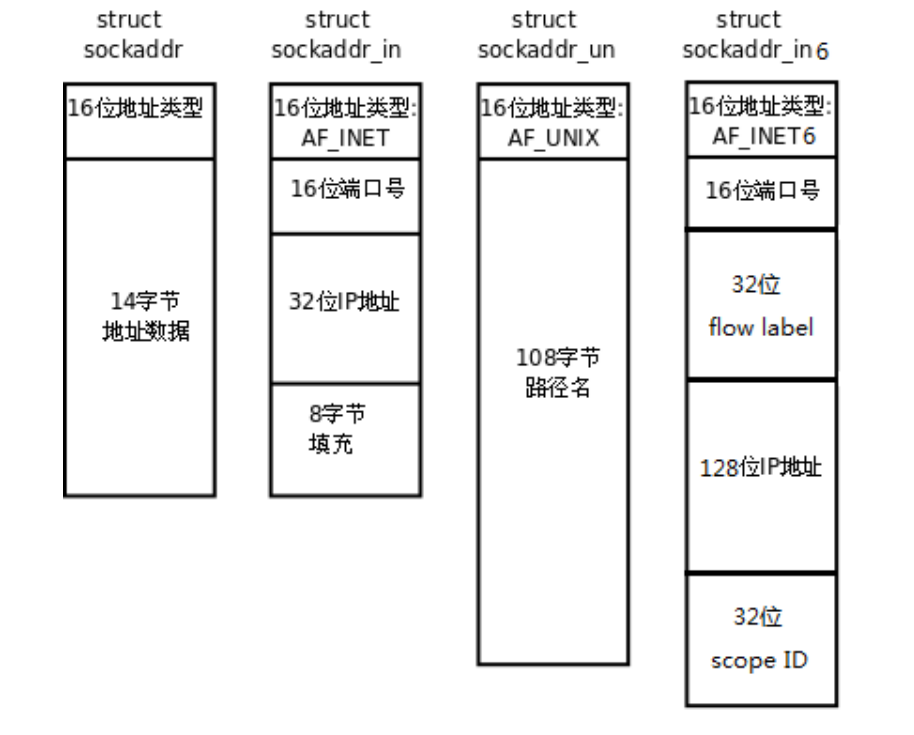
socket地址理解
socket介绍 套接字的基本概念 1. 套接字的定义: 套接字(socket)是计算机网络中用于通信的端点,它抽象了不同主机上应用进程之间双向通信的机制。 2. 套接字的作用: 套接字连接应用进程与网络协议栈,使…...

Gopeed的高级用法
Gopeed是一个开源全平台下载器,具体简介请参考: “狗屁下载器”?Gopeed - 开源全平台下载器 (免费轻量 / 比 Aria2 好用 / 远程下载) - 异次元软件世界 (iplaysoft.com) 这里主要介绍下自己摸索出来的 Gopeed 的高级做法。 有的网站添加的…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
