吴恩达深度学习笔记:超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)3.4-3.5
目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)
- 3.4 归一化网络的激活函数(Normalizing activations in a network)
- 3.5 将 Batch Norm 拟合进神经网络(Fitting Batch Norm into a neural network)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)
3.4 归一化网络的激活函数(Normalizing activations in a network)
在深度学习兴起后,最重要的一个思想是它的一种算法,叫做 Batch 归一化,由 Sergey loffe和Christian Szegedy 两位研究者创造。Batch归一化会使你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参数的范围会更加庞大,工作效果也很好,也会是你的训练更加容易,甚至是深层网络。让我们来看看 Batch 归一化是怎么起作用的吧。

当训练一个模型,比如 logistic 回归时,你也许会记得,归一化输入特征可以加快学习过程。你计算了平均值,从训练集中减去平均值,计算了方差,接着根据方差归一化你的数据集,在之前的视频中我们看到,这是如何把学习问题的轮廓,从很长的东西,变成更圆的东西,更易于算法优化。所以这是有效的,对 logistic 回归和神经网络的归一化输入特征值而言。
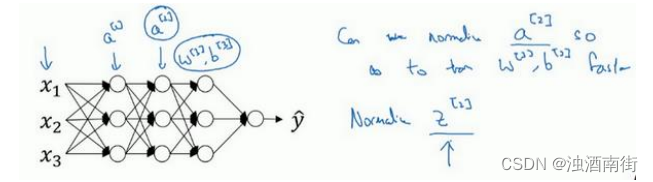
那么更深的模型呢?你不仅输入了特征值𝑥,而且这层有激活值 a [ 1 ] a^{[1]} a[1],这层有激活值 a [ 2 ] a^{[2]} a[2]等等。如果你想训练这些参数,比如 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3],那归一化 a [ 2 ] a^{[2]} a[2]的平均值和方差岂不是很好?以便使 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3]的训练更有效率。在 logistic 回归的例子中,我们看到了如何归一化 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,会帮助你更有效的训练w和b。
所以问题来了,对任何一个隐藏层而言,我们能否归一化a值,在此例中,比如说 a [ 2 ] a^{[2]} a[2]的值,但可以是任何隐藏层的,以更快的速度训练 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3],因为 a [ 2 ] a^{[2]} a[2]是下一层的输入值,所以就会影响 w [ 3 ] w^{[3]} w[3], b [ 3 ] b^{[3]} b[3]的训练。简单来说,这就是 Batch 归一化的作用。尽管严格来说,我们真正归一化的不是 a [ 2 ] a^{[2]} a[2],而是 z [ 2 ] z^{[2]} z[2],深度学习文献中有一些争论,关于在激活函数之前是否应该将值 z [ 2 ] z^{[2]} z[2]归一化,或是否应该在应用激活函数 a [ 2 ] a^{[2]} a[2]后再规范值。实践中,经常做的是归一化 z [ 2 ] z^{[2]} z[2],所以这就是我介绍的版本,我推荐其为默认选择,那下面就是 Batch 归一化的使用方法。
在神经网络中,已知一些中间值,假设你有一些隐藏单元值,从 z ( 1 ) z^{(1)} z(1)到 z ( m ) z^{(m)} z(m),这些来源于隐藏层,所以这样写会更准确,
即 z [ l ] ( i ) z^{[l](i)} z[l](i)为隐藏层,𝑖从 1 到𝑚,但这样书写,我要省略𝑙及方括号,以便简化这一行的符号。所以已知这些值,如下,你要计算平均值,强调一下,所有这些都是针对𝑙层,但我省略𝑙及方括号,然后用正如你常用的那个公式计算方差,接着,你会取每个𝑧(𝑖)值,使其规范化,方法如下,减去均值再除以标准偏差,为了使数值稳定,通常将 ϵ \epsilon ϵ作为分母,以防防𝜎 = 0的情况。
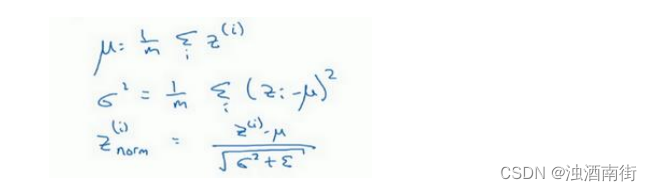
所以现在我们已把这些z值标准化,化为含平均值 0 和标准单位方差,所以𝑧的每一个分量都含有平均值 0 和方差 1,但我们不想让隐藏单元总是含有平均值 0 和方差 1,也许隐藏单元有了不同的分布会有意义,所以我们所要做的就是计算,我们称之为 z ^ ( i ) \hat{z}^{(i)} z^(i), z ^ ( i ) = γ z n o r m ( i ) + β \hat{z}^{(i)} = \gamma z_{norm}^{(i)} +\beta z^(i)=γznorm(i)+β,这里𝛾和𝛽是你模型的学习参数,所以我们使用梯度下降或一些其它类似梯度下降的算法,比如 Momentum 或者 Nesterov,Adam,你会更新𝛾和𝛽,正如更新神经网络的权重一样。
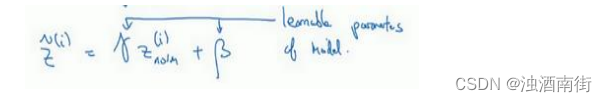
请注意𝛾和𝛽的作用是,你可以随意设置𝑧̃(𝑖)的平均值,事实上,如果 γ = σ 2 + ϵ \gamma = \sqrt{\sigma^2 + \epsilon} γ=σ2+ϵ ,如果𝛾等于这个分母项( z n o r m ( i ) = z ( i ) − μ σ 2 + ϵ z_{norm}^{(i)} =\frac{z^{(i)} -\mu}{\sqrt{\sigma^2 + \epsilon}} znorm(i)=σ2+ϵz(i)−μ中的分母), β \beta β等于 μ \mu μ,这里的这个值是 z n o r m ( i ) = z ( i ) − μ σ 2 + ϵ z_{norm}^{(i)} =\frac{z^{(i)} -\mu}{\sqrt{\sigma^2 + \epsilon}} znorm(i)=σ2+ϵz(i)−μ中的 μ \mu μ,那么 γ z n o r m ( i ) + β \gamma z_{norm}^{(i)} + \beta γznorm(i)+β的作用在于,它会精确转化这个方程,如果这些成立( γ = σ 2 + ϵ \gamma = \sqrt{\sigma^2 + \epsilon} γ=σ2+ϵ, β = μ \beta =\mu β=μ),那么 z ^ ( i ) = z ( i ) \hat{z}^{(i)} = z^{(i)} z^(i)=z(i)。
通过对𝛾和𝛽合理设定,规范化过程,即这四个等式,从根本来说,只是计算恒等函数,通过赋予𝛾和𝛽其它值,可以使你构造含其它平均值和方差的隐藏单元值。

所以,在网络匹配这个单元的方式,之前可能是用 z ( 1 ) z^{(1)} z(1), z ( 2 ) z^{(2)} z(2)等等,现在则会用 z ^ i \hat{z}^{i} z^i取代 z ( i ) z^{(i)} z(i),方便神经网络中的后续计算。如果你想放回[𝑙],以清楚的表明它位于哪层,你可以把它放这。
所以我希望你学到的是,归一化输入特征X是怎样有助于神经网络中的学习,Batch 归一化的作用是它适用的归一化过程,不只是输入层,甚至同样适用于神经网络中的深度隐藏层。你应用 Batch 归一化了一些隐藏单元值中的平均值和方差,不过训练输入和这些隐藏单元值的一个区别是,你也许不想隐藏单元值必须是平均值 0 和方差 1。

比如,如果你有 sigmoid 激活函数,你不想让你的值总是全部集中在这里,你想使它们有更大的方差,或不是 0 的平均值,以便更好的利用非线性的 sigmoid 函数,而不是使所有的值都集中于这个线性版本中,这就是为什么有了𝛾和𝛽两个参数后,你可以确保所有的 z ( i ) z^{(i)} z(i)值可以是你想赋予的任意值,或者它的作用是保证隐藏的单元已使均值和方差标准化。那里,均值和方差由两参数控制,即𝛾和𝛽,学习算法可以设置为任何值,所以它真正的作用是,使隐藏单元值的均值和方差标准化,即 z ( i ) z^{(i)} z(i)有固定的均值和方差,均值和方差可以是 0 和 1,也可以是其它值,它是由𝛾和𝛽两参数控制的。
我希望你能学会怎样使用 Batch 归一化,至少就神经网络的单一层而言,在下一个视频中,我会教你如何将 Batch 归一化与神经网络甚至是深度神经网络相匹配。对于神经网络许多不同层而言,又该如何使它适用,之后,我会告诉你,Batch 归一化有助于训练神经网络的原因。所以如果觉得 Batch 归一化起作用的原因还显得有点神秘,那跟着我走,在接下来的两个视频中,我们会弄清楚。
3.5 将 Batch Norm 拟合进神经网络(Fitting Batch Norm into a neural network)
你已经看到那些等式,它可以在单一隐藏层进行 Batch 归一化,接下来,让我们看看它是怎样在深度网络训练中拟合的吧。

假设你有一个这样的神经网络,我之前说过,你可以认为每个单元负责计算两件事。第一,它先计算z,然后应用其到激活函数中再计算a,所以我可以认为,每个圆圈代表着两步的计算过程。同样的,对于下一层而言,那就是 z 1 [ 2 ] z_1^{[2]} z1[2]和 z 2 [ 2 ] z_2^{[2]} z2[2]等。所以如果你没有应用 Batch 归一化,你会把输入𝑋拟合到第一隐藏层,然后首先计算 z [ 1 ] z^{[1]} z[1],这是由 w [ 1 ] w^{[1]} w[1]和 b [ 1 ] b^{[1]} b[1]两个参数控制的。接着,通常而言,你会把 z [ 1 ] z^{[1]} z[1]拟合到激活函数以计算 a [ 1 ] a^{[1]} a[1]。但 Batch 归一化的做法是将 z [ 1 ] z^{[1]} z[1]值进行 Batch 归一化,简称 BN,此过程将由 β [ 1 ] \beta^{[1]} β[1]和 γ [ 1 ] \gamma^{[1]} γ[1]两参数控制,这一操作会给你一个新的规范化的 z [ 1 ] z^{[1]} z[1]值( z ^ [ 1 ] \hat{z}^[1] z^[1]),然后将其输入激活函数中得到 a [ 1 ] a^{[1]} a[1],即 a [ 1 ] = g [ 1 ] ( z ^ [ l ] ) a^{[1]} = g^{[1]}(\hat{z}^{[l]}) a[1]=g[1](z^[l])。
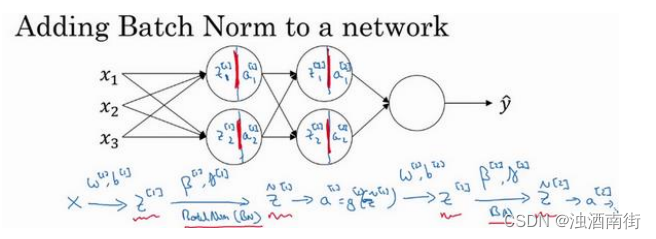
现在,你已在第一层进行了计算,此时 Batch 归一化发生在𝑧的计算和𝑎之间,接下来,你需要应用 a [ 1 ] a^{[1]} a[1]值来计算 z [ 2 ] z^{[2]} z[2],此过程是由 w [ 2 ] w^{[2]} w[2]和 b [ 2 ] b^{[2]} b[2]控制的。与你在第一层所做的类似,你会将 z [ 2 ] z^{[2]} z[2]进行 Batch 归一化,现在我们简称 BN,这是由下一层的 Batch 归一化参数所管制的,即 β [ 2 ] \beta^{[2]} β[2]和 γ [ 2 ] \gamma^{[2]} γ[2],现在你得到 z ^ [ 2 ] \hat{z}^{[2]} z^[2],再通过激活函数计算出 a [ 2 ] a^{[2]} a[2]等等。
所以需要强调的是 Batch 归一化是发生在计算𝑧和𝑎之间的。直觉就是,与其应用没有归一化的𝑧值,不如用归一过的 z ^ \hat{z} z^,这是第一层( z ^ [ 1 ] \hat{z}^{[1]} z^[1])。第二层同理,与其应用没有规范过的 z [ 2 ] z^{[2]} z[2]值,不如用经过方差和均值归一后的 z ^ [ 2 ] \hat{z}^{[2]} z^[2]。所以,你网络的参数就会是 w [ 1 ] w^{[1]} w[1], b [ 1 ] b^{[1]} b[1], w [ 2 ] w^{[2]} w[2]和 b [ 2 ] b^{[2]} b[2]等等,我们将要去掉这些参数。但现在,想象参数 w [ 1 ] w^{[1]} w[1], b [ 1 ] b^{[1]} b[1]到 w [ l ] w^{[l]} w[l], b [ l ] b^{[l]} b[l],我们将另一些参数加入到此新网络中 β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2], γ [ 1 ] \gamma^{[1]} γ[1], γ [ 2 ] \gamma^{[2]} γ[2]等等。对于应用 Batch 归一化的每一层而言。需要澄清的是,请注意,这里的这些 β \beta β( β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2]等等)和超参数 β \beta β没有任何关系,下一张幻灯片中会解释原因,后者是用于 Momentum 或计算各个指数的加权平均值。Adam 论文的作者,在论文里用 β \beta β代表超参数。Batch 归一化论文的作者,则使用 β \beta β代表此参数( β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2]等等),但这是两个完全不同的 β \beta β。我在两种情况下都决定使用 β \beta β,以便你阅读那些原创的论文,但 Batch 归一化学习参数 β [ 1 ] \beta^{[1]} β[1], β [ 2 ] \beta^{[2]} β[2]等等和用于 Momentum、Adam、RMSprop 算法中的𝛽不同。

所以现在,这是你算法的新参数,接下来你可以使用想用的任何一种优化算法,比如使用梯度下降法来执行它。
举个例子,对于给定层,你会计算 d β [ l ] d\beta^{[l]} dβ[l],接着更新参数 β \beta β为 β [ l ] \beta^{[l]} β[l] = β [ l ] \beta^{[l]} β[l] − α d β [ l ] \alpha d\beta^{[l]} αdβ[l]。你也可以使用 Adam 或 RMSprop 或 Momentum,以更新参数 β \beta β和𝛾,并不是只应用梯度下降法。
即使在之前的视频中,我已经解释过 Batch 归一化是怎么操作的,计算均值和方差,减去均值,再除以方差,如果它们使用的是深度学习编程框架,通常你不必自己把 Batch 归一化步骤应用于 Batch 归一化层。因此,探究框架,可写成一行代码,比如说,在 TensorFlow框架中,你可以用这个函数(tf.nn.batch_normalization)来实现 Batch 归一化,我们稍后讲解,但实践中,你不必自己操作所有这些具体的细节,但知道它是如何作用的,你可以更好的理解代码的作用。但在深度学习框架中,Batch 归一化的过程,经常是类似一行代码的东西。
所以,到目前为止,我们已经讲了 Batch 归一化,就像你在整个训练站点上训练一样,或就像你正在使用 Batch 梯度下降法。
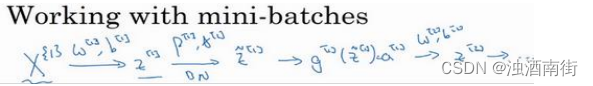
实践中,Batch 归一化通常和训练集的 mini-batch 一起使用。你应用 Batch 归一化的方式就是,你用第一个 mini-batch(X^{{1}}),然后计算 z [ 1 ] z^{[1]} z[1],这和上张幻灯片上我们所做的一样,应用参数 w [ 1 ] w^{[1]} w[1]和 b [ 1 ] b^{[1]} b[1],使用这个 m i n i − b a t c h ( X 1 ) mini-batch(X^{{1}}) mini−batch(X1)。接着,继续第二个 mini-batch(X^{{2}}),接着Batch 归一化会减去均值,除以标准差,由 β [ 1 ] \beta^{[1]} β[1]和 γ [ 1 ] \gamma^{[1]} γ[1]重新缩放,这样就得到了 z ^ [ 1 ] \hat{z}^{[1]} z^[1],而所有的这些都是在第一个 mini-batch 的基础上,你再应用激活函数得到 a [ 1 ] a^{[1]} a[1]。然后用 w [ 2 ] w^{[2]} w[2]和 b [ 2 ] b^{[2]} b[2]计算 z [ 2 ] z^{[2]} z[2],等等,所以你做的这一切都是为了在第一个 mini-batch( X 1 X^{{1}} X1)上进行一步梯度下降法。
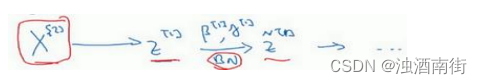
类似的工作,你会在第二个 mini-batch(KaTeX parse error: Expected 'EOF', got '}' at position 7: X^[{2}}̲)上计算 z [ 1 ] z^{[1]} z[1],然后用 Batch 归一化来计算 z ^ [ 1 ] \hat{z}^{[1]} z^[1],所以 Batch 归一化的此步中,你用第二个 mini-batch(KaTeX parse error: Expected 'EOF', got '}' at position 7: X^[{2}}̲)中的数据使 z ^ [ 1 ] \hat{z}^{[1]} z^[1]归一化,这里的 Batch 归一化步骤也是如此,让我们来看看在第二个 mini-batch( X 2 X^{{2}} X2)中的例子,在mini-batch 上计算 z [ 1 ] z^{[1]} z[1]的均值和方差,重新缩放的 β \beta β和 γ \gamma γ得到 z [ 1 ] z^{[1]} z[1],等等。
然后在第三个 mini-batch( X 3 X^{{3}} X3)上同样这样做,继续训练。
现在,我想澄清此参数的一个细节。先前我说过每层的参数是 w [ l ] w^{[l]} w[l]和 b [ l ] b^{[l]} b[l],还有 β [ l ] \beta^{[l]} β[l]和 γ [ l ] \gamma^{[l]} γ[l],请注意计算𝑧的方式如下, z [ l ] z^{[l]} z[l] = w [ l ] a [ l − 1 ] + b [ l ] w^{[l]}a^{[l−1]} + b^{[l]} w[l]a[l−1]+b[l],但 Batch 归一化做的是,它要看这个 mini-batch,先将 z [ l ] z^{[l]} z[l]归一化,结果为均值 0 和标准方差,再由 β \beta β和 γ \gamma γ重缩放,但这意味着,无论 b [ l ] b^{[l]} b[l]的值是多少,都是要被减去的,因为在 Batch 归一化的过程中,你要计算 z [ l ] z^{[l]} z[l]的均值,再减去平均值,在此例中的 mini-batch 中增加任何常数,数值都不会改变,因为加上的任何常数都将会被均值减去所抵消。
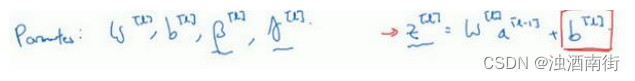
所以,如果你在使用 Batch 归一化,其实你可以消除这个参数( b [ l ] b^{[l]} b[l]),或者你也可以,暂时把它设置为 0,那么,参数变成 z [ l ] z^{[l]} z[l] = w [ l ] a [ l − 1 ] w^{[l]}a^{[l−1]} w[l]a[l−1],然后你计算归一化的 z [ l ] z^{[l]} z[l], z ^ [ l ] \hat{z}^{[l]} z^[l] = γ [ l ] \gamma^{[l]} γ[l] z [ l ] z^{[l]} z[l]+ β [ l ] \beta^{[l]} β[l],你最后会用参数 β [ l ] \beta^{[l]} β[l],以便决定 z ^ [ l ] \hat{z}^{[l]} z^[l]的取值,这就是原因。

所以总结一下,因为 Batch 归一化超过了此层 z [ l ] z^{[l]} z[l]的均值,𝑏[𝑙]这个参数没有意义,所以,你必须去掉它,由 β [ l ] \beta^{[l]} β[l]代替,这是个控制参数,会影响转移或偏置条件。
最后,请记住 z [ l ] z^{[l]} z[l]的维数,因为在这个例子中,维数会是( n [ l ] n^{[l]} n[l], 1), β [ l ] \beta^{[l]} β[l]的尺寸为( n [ l ] n^{[l]} n[l], 1),如果是 l 层隐藏单元的数量,那 β [ l ] \beta^{[l]} β[l]和 γ [ l ] \gamma^{[l]} γ[l]的维度也是( n [ l ] n^{[l]} n[l], 1),因为这是你隐藏层的数量,你有 n [ l ] n^{[l]} n[l]隐藏单元,所以 β [ l ] \beta^{[l]} β[l]和 γ [ l ] \gamma^{[l]} γ[l]用来将每个隐藏层的均值和方差缩放为网络想要的值。

让我们总结一下关于如何用 Batch 归一化来应用梯度下降法,假设你在使用 mini-batch梯度下降法,你运行𝑡 = 1到 batch 数量的 for 循环,你会在 mini-batch X t X^{{t}} Xt上应用正向 prop,每个隐藏层都应用正向 prop,用 Batch 归一化代替 z [ l ] z^{[l]} z[l]为 z ^ [ l ] \hat{z}^{[l]} z^[l]。接下来,它确保在这个 mini-batch 中,𝑧值有归一化的均值和方差,归一化均值和方差后是 z ^ [ l ] \hat{z}^{[l]} z^[l],然后,你用反向 prop 计算 d w [ l ] dw^{[l]} dw[l]和 d b [ l ] db^{[l]} db[l],及所有 l 层所有的参数, d β [ l ] d\beta^{[l]} dβ[l]和 d γ [ l ] d\gamma^{[l]} dγ[l]。尽管严格来说,因为你要去掉𝑏,这部分其实已经去掉了。最后,你更新这些参数: w [ l ] w^{[l]} w[l]= w [ l ] − α d w [ l ] w^{[l]} − \alpha dw^{[l]} w[l]−αdw[l],和以前一样, β [ l ] \beta^{[l]} β[l]= β [ l ] − α d β [ l ] \beta^{[l]} −\alpha d\beta^{[l]} β[l]−αdβ[l],对于𝛾也是如此 γ [ l ] \gamma^{[l]} γ[l]= γ [ l ] − α d γ [ l ] \gamma^{[l]} − \alpha d\gamma^{[l]} γ[l]−αdγ[l]。
如果你已将梯度计算如下,你就可以使用梯度下降法了,这就是我写到这里的,但也适用于有 Momentum、RMSprop、Adam 的梯度下降法。与其使用梯度下降法更新 mini-batch,你可以使用这些其它算法来更新,我们在之前几个星期中的视频中讨论过的,也可以应用其它的一些优化算法来更新由 Batch 归一化添加到算法中的 β \beta β 和 γ \gamma γ参数。

我希望,你能学会如何从头开始应用 Batch 归一化,如果你想的话。如果你使用深度学习编程框架之一,我们之后会谈。希望,你可以直接调用别人的编程框架,这会使 Batch归一化的使用变得很容易。
现在,以防 Batch 归一化仍然看起来有些神秘,尤其是你还不清楚为什么其能如此显著的加速训练,我们进入下一个视频,详细讨论 Batch 归一化为何效果如此显著,它到底在做什么。
相关文章:

吴恩达深度学习笔记:超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)3.4-3.5
目录 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter …...

牛客NC362 字典序排列【中等 DFS Java/Go/PHP】
题目 题目链接: https://www.nowcoder.com/practice/de49cf70277048518314fbdcaba9b42c 解题方法 DFS,剪枝Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回…...
、__DIR__、__FILE__的区别)
PHP获取文件路径getcwd()、__DIR__、__FILE__的区别
getcwd() getcwd() 是一个函数,它返回当前工作目录(CWD)的完整路径。当前工作目录是脚本开始执行时所在的目录,除非在脚本执行过程中通过 chdir() 函数进行了更改。 $cwd getcwd(); echo $cwd; // 输出当前工作目录的完整路径…...

Kafka(十三)监控与告警
目录 Kafka监控与告警1 解决方案1.2 基础知识JMX监控指标代理查看KafkaJMX远程端口 1.3 真实案例Kafka Exporter:PromethusPromethus Alert ManagerGrafana 1.3 实际操作部署监控和告警系统1.2.1 部署Kafka Exporter1.2.2 部署Prometheus1.2.3 部署AlertManger1.2.4 添加告警规…...

SBC3568启动升级,灵活更换动画logo
今天小智将会带着大家体验如何在openharmony sdk内替换开机logo和动态动画。 1. 更换开机logo 开机logo分为uboot阶段【logo.bmp】和kernel阶段【logo_kernel.bmp】的logo两个文件,对图片的要求是:必须为bmp格式,8或者24位深,且…...
)
v-if 与 v-show(vue3条件渲染)
v-if 是“真正”的条件渲染,因为它会确保在切换过程中条件块内的事件监听器和子组件适当地被销毁和重建。 v-if 也是惰性的:如果在初始渲染时条件为假,则什么也不做——直到条件第一次变为真时,才会开始渲染条件块。 相比之下&a…...

nuxt: generate打包后访问资源404问题
现象 使用Nuxt.js开发的个人页面,部署到nginx服务器中,/_nuxt/*.js、/_nuxt/*.css等静态问题不能访问,提示404错误。 而我们的这些资源文件是存在的。 解决方法 加上此处代码进行上下文配置 baseURL: /nuxt/ 此时在nginx配置 /nuxt 代理 lo…...
)
【图像超分】论文精读:Residual Non-local Attention Networks for Image Restoration(RNAN)
第一次来请先看这篇文章:【超分辨率(Super-Resolution)】关于【超分辨率重建】专栏的相关说明,包含专栏简介、专栏亮点、适配人群、相关说明、阅读顺序、超分理解、实现流程、研究方向、论文代码数据集汇总等) 文章目录 前言Abstract1 INTRODUCTION2 RELATED WORK3 RESIDU…...

AI大模型:大数据+大算力+强算法
前言:好久不见,甚是想念,我是辣条,我又回来啦,兄弟们,一别两年,还有多少老哥们在呢? 目录 一年半没更文我干啥去了? AI大模型火了 人工智能 大模型的理解 为什么学习…...
同名在线查询系统微信小程序源码下载支持多种流量主,附带系统教程
同名在线查询系统微信小程序源码下载支持多种流量主这是一款支持查询同名的一款微信小程序 该款小程序支持多种查询模式 重名查询,热度查询,概率香查询 源码免费下载地址抄笔记(chaobiji.cn)...

2024年5月26日 十二生肖 今日运势
小运播报:2024年5月26日,星期日,农历四月十九 (甲辰年己巳月庚寅日),法定节假日。 红榜生肖:马、猪、狗 需要注意:牛、蛇、猴 喜神方位:西北方 财神方位:…...

Vue 3 组件基础与模板语法详解
title: Vue 3 组件基础与模板语法详解 date: 2024/5/24 16:31:13 updated: 2024/5/24 16:31:13 categories: 前端开发 tags: Vue3特性CompositionAPITeleportSuspenseVue3安装组件基础模板语法 Vue 3 简介 1. Vue 3 的新特性 Vue 3引入了许多新的特性,以提高框…...

ACM实训冲刺第十八天
统计元音 代码 需要注意的是getchar()和gets(s) #include<stdio.h> #include<string.h> int main(){//测试实例个数int n;scanf("%d",&n) ;char s[100];getchar();while(n--){gets(s);int cnta0,cnte0,cnti0,cnto0,cntu0;for(int j0;j<strlen(…...

22AP70/SS927
Hi3519AV200又叫SS927V100和SD3402V100,或者叫22AP70,是一颗面向市场推出的专业超高清智能网络录像机SoC,专门用来替换之前的Hi3519AV100,2023年推出的业界AI-ISP超高性价比芯片!该芯片最高支持四路sensor输入…...

C++实现的代码行数统计器
代码在GitHubMaolinYe/CodeCounter: C20实现的代码统计器,代码量小于100行,可以统计目录下所有代码文件的行数 (github.com) 前段时间到处面试找实习,有技术负责人的负责人问我C写过多少行,5万还是10万,用来评估熟练度…...
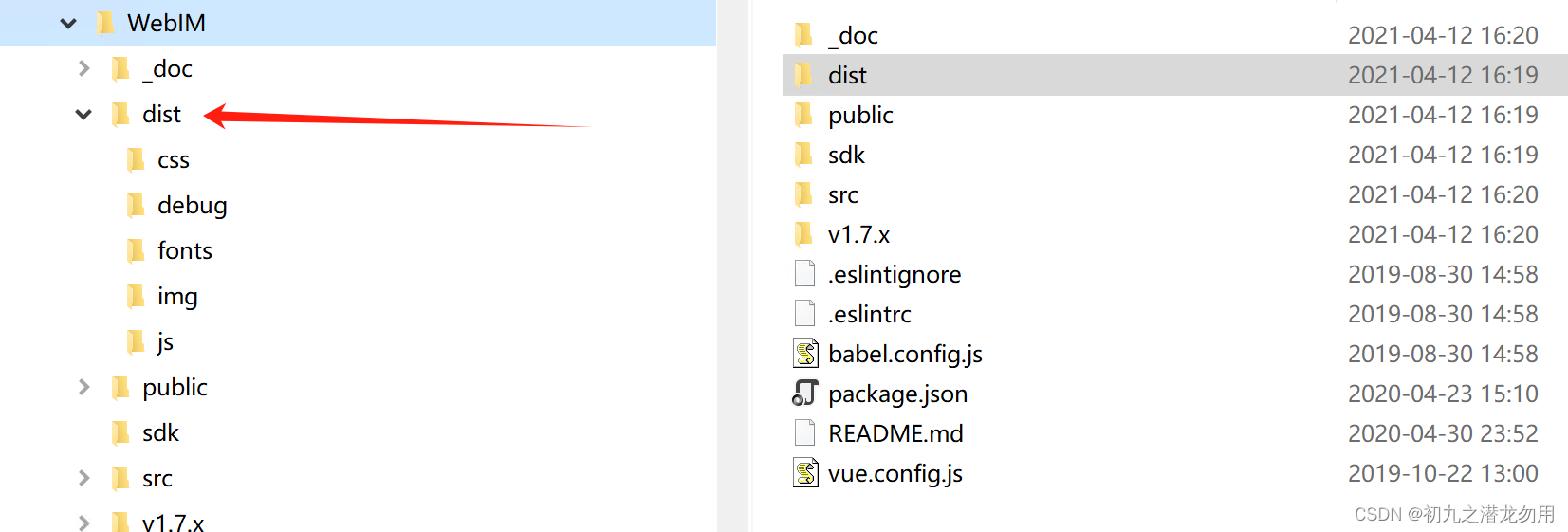
C# 结合 JS 暴改腾讯 IM SDK Demo
目录 关于腾讯 IM SDK Demo 范例运行环境 设计思路 服务端生成地址 IM 服务端接收 IM 客户端程序 小结 关于腾讯 IM SDK Demo 腾讯云即时通信 IM SDK 提供了单聊、群聊、关系链、消息漫游、群组管理、资料管理、直播弹幕等功能,并提供完备的 App 接入及管…...

【Web】CISCN 2024初赛 题解(全)
目录 Simple_php easycms easycms_revenge ezjava mossfern sanic Simple_php 用php -r进行php代码执行 因为ban了引号,考虑hex2bin,将数字转为字符串 php -r eval(hex2bin(16进制)); 注意下面这段报错,因为加不了引号,开…...
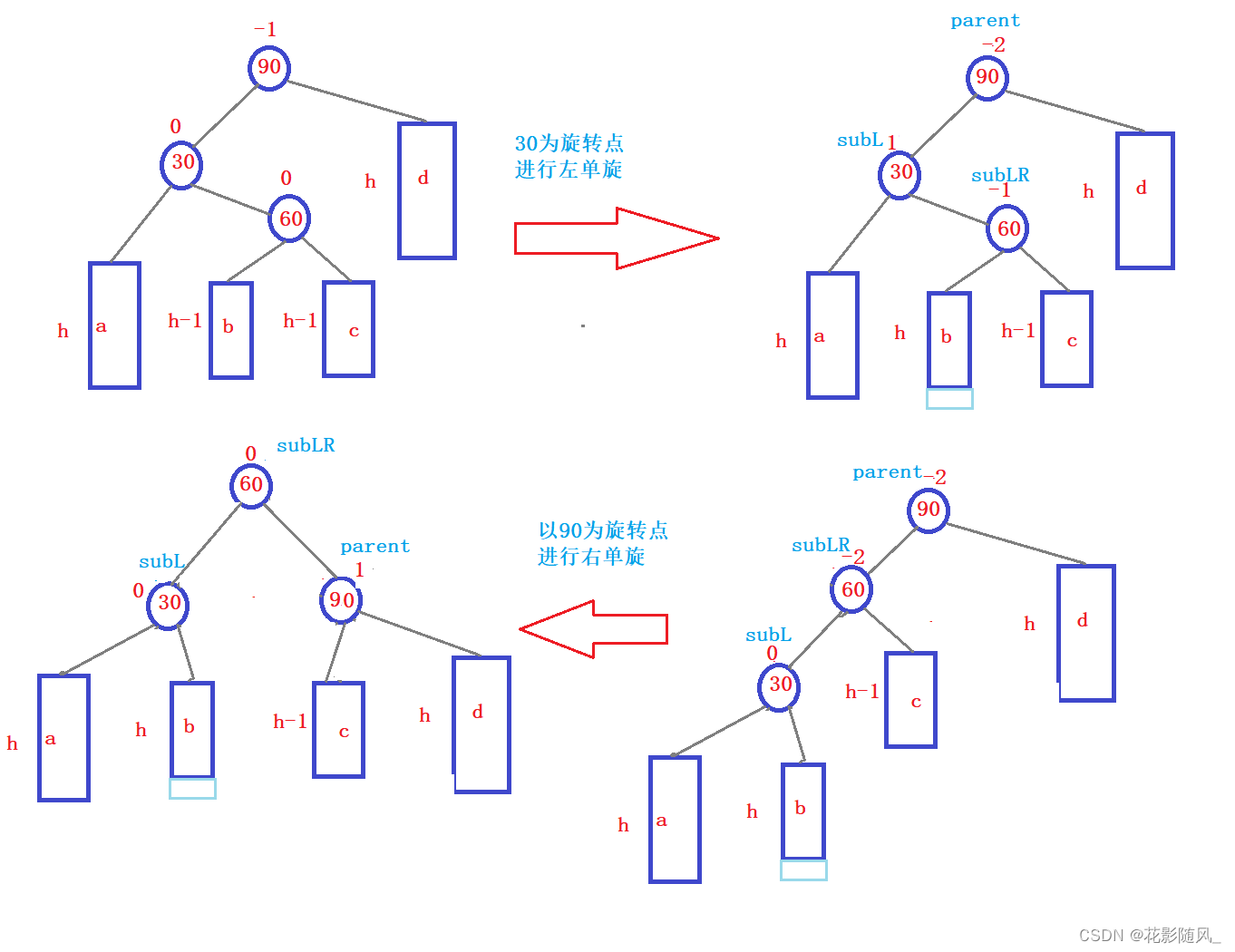
【C++进阶】AVL树
0.前言 前面我们已经学习过二叉搜索树了,但如果我们是用二叉搜索树来封装map和set等关联式容器是有缺陷的,很可能会退化为单分支的情况,那样效率就极低了,那么有没有方法来弥补二叉搜索树的缺陷呢? 那么AVL树就出现了&…...
云部署最简单python web
最近在玩云主机,考虑将简单的web应用装上去,通过广域网访问一下,代码很简单,所以新手几乎不会碰到什么问题。 from flask import Flaskapp Flask(__name__)app.route(/) def hello_world():return Hello, World!app.route(/gree…...
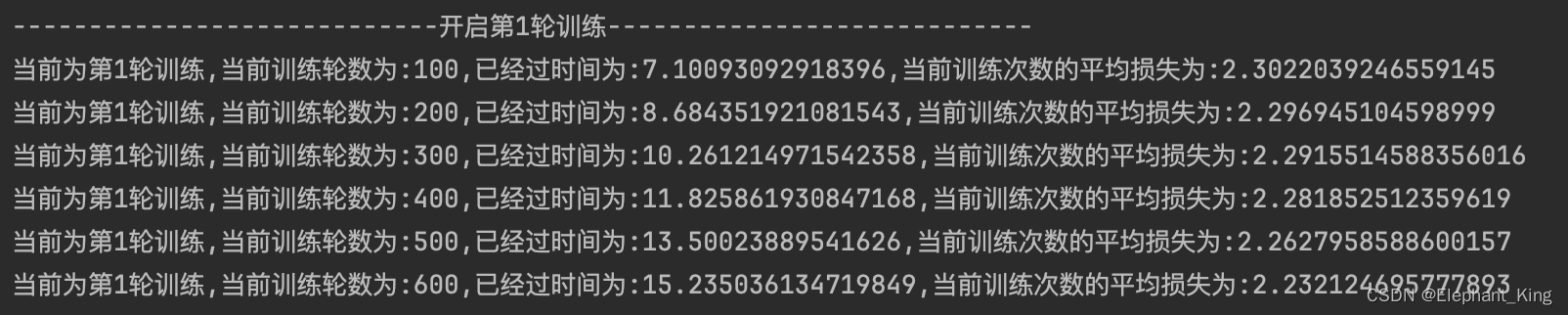
【Pytorch】【MacOS】14.m1芯片使用mps进行深度模型训练
读者要先自行安装python以及anaconda,并且配置pytorch环境 第一步 测试环境 import torch # 判断macOS的版本是否支持 print(torch.backends.mps.is_available()) # 判断mps是否可用 print(torch.backends.mps.is_built())如果第一个语句为False,说明当前…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
