大胆预测:计算机将要回暖
中概财报集体亮眼
虽然最近几天恒指(港股)稍有回落,但年线仍有 9% 的上涨。
过去三年,恒指分别下跌 14.08%、15.46% 和 13.82%。
而在近期,国内各大互联网都公布了财报,别看各个大厂的作妖不断,但这次似乎真的有点「否极泰来」的意思了:
-
腾讯净利润 418.89 亿,同比增长 62.12%
-
拼多多净利润 279.98 亿,同比增长 245.61%
-
阿里净利润 244.18 亿,同比增长 -10.80%
-
网易净利润 76.34 亿,同比增长 13.02%
-
京东净利润 71.30 亿,同比增长 13.88%
-
小米净利润 64.9 亿,同比增长 100%
-
百度净利润 54.48 亿,同比增长 -6.47%
-
携程净利润 43.12 亿,同比增长 27.76%
-
快手净利润 41.19 亿,同比增长 571.82%
现在提到「互联网」和「计算机」,大多数声音还都是「裁员」、「人挤人」和「找不到工作」,但财务数据才是真实的,而且从「金融资本市场」到「劳动力市场」往往有 1~2 年的滞后性。
现在往回看,其实国内互联网的转向是从 2021 年年初就开始的,但 2021 年的招聘市场,大家都知道的。流行语是「打得火热」、「跳槽薪资翻倍」和「应届生实习工资水涨船高,直接倒挂老员工」,所谓的「裁员」和「寒气」是从 2022 下半年才开始大面积盛行的。
所以根据现在掌握的信息来看,我可以大胆给出结论:计算机看不到希望的长夜已经过去,回暖是大概率的事情。
我给大家的建议,抓紧学习,厚积薄发,好日子快回来了。
如果因为现在的行情决定「转行」或者「放弃转码」,大概率不会变得更好,而且可能还会成为倒在黎明的那一批。
...
回归主题。
来一道和「字节跳动」相关的题目(不要问我为啥最近都是字节跳动,宇宙厂的投稿太多了 🤣
题目描述
平台:LeetCode
题号:940
给定一个字符串 s,计算 s 的 不同非空子序列 的个数。
因为结果可能很大,所以返回答案需要对 取余 。
字符串的 子序列 是经由原字符串删除一些(也可能不删除)字符但不改变剩余字符相对位置的一个新字符串。
例如,"ace" 是 "abcde" 的一个子序列,但 "aec" 不是。
示例 1:
输入:s = "abc"
输出:7
解释:7 个不同的子序列分别是 "a", "b", "c", "ab", "ac", "bc", 以及 "abc"。
示例 2:
输入:s = "aba"
输出:6
解释:6 个不同的子序列分别是 "a", "b", "ab", "ba", "aa" 以及 "aba"。
示例 3:
输入:s = "aaa"
输出:3
解释:3 个不同的子序列分别是 "a", "aa" 以及 "aaa"。
提示:
-
-
s仅由小写英文字母组成
序列 DP
为了方便,我们令 s 下标从 1 开始,定义 为考虑前 i 个字符,且结尾字符为 j 的不同子序列的个数,其中 j 的范围为 代指小写字符 a-z。
我们有显而易见的初始化条件 ,最终答案为 。
不失一般性考虑 该如何转移,根据 是否为 j 进行分情况讨论:
-
: 由于状态定义限定了结尾字符必须是 ,因而 必然不会用到,此时有:
-
: 此时 可作为结尾元素,同时由于我们统计的是「不同」的子序列个数,因而「以 结尾的子序列方案数」与「以 结尾的子序列方案数」完全等价。 对于以 作为子序列结尾字符的方案数,容易想到其方案数等于「 单独作为子序列」+「 拼接在其余子序列后面形成新子序列」,即有:
Java 代码:
class Solution {
int MOD = (int)1e9+7;
public int distinctSubseqII(String s) {
int n = s.length(), ans = 0;
int[][] f = new int[n + 1][26];
for (int i = 1; i <= n; i++) {
int c = s.charAt(i - 1) - 'a';
for (int j = 0; j < 26; j++) {
if (c != j) {
f[i][j] = f[i - 1][j];
} else {
int cur = 1;
for (int k = 0; k < 26; k++) cur = (cur + f[i - 1][k]) % MOD;
f[i][j] = cur;
}
}
}
for (int i = 0; i < 26; i++) ans = (ans + f[n][i]) % MOD;
return ans;
}
}
C++ 代码:
class Solution {
public:
int distinctSubseqII(string s) {
int n = s.length(), MOD = 1e9 + 7;
vector<vector<int>> f(n + 1, vector<int>(26, 0));
for (int i = 1; i <= n; ++i) {
int c = s[i - 1] - 'a';
for (int j = 0; j < 26; ++j) {
if (c != j) {
f[i][j] = f[i - 1][j];
} else {
int cur = 1;
for (int k = 0; k < 26; ++k) cur = (cur + f[i - 1][k]) % MOD;
f[i][j] = cur;
}
}
}
int ans = 0;
for (int i = 0; i < 26; ++i) ans = (ans + f[n][i]) % MOD;
return ans;
}
};
Python 代码:
class Solution:
def distinctSubseqII(self, s: str) -> int:
n, MOD = len(s), 1e9+7
f = [[0] * 26 for _ in range(n + 1)]
for i in range(1, n + 1):
c = ord(s[i - 1]) - ord('a')
for j in range(26):
f[i][j] = f[i - 1][j] if c != j else (1 + sum(f[i - 1])) % MOD
return int(sum(f[n]) % MOD)
TypeScript 代码:
function distinctSubseqII(s: string): number {
const MOD = 1e9+7
let n = s.length, ans = 0
const f = new Array<Array<number>>(n + 1)
for (let i = 0; i <= n; i++) f[i] = new Array<number>(26).fill(0)
for (let i = 1; i <= n; i++) {
const c = s.charCodeAt(i - 1) - 'a'.charCodeAt(0)
for (let j = 0; j < 26; j++) {
if (c != j) {
f[i][j] = f[i - 1][j]
} else {
let cur = 1
for (let k = 0; k < 26; k++) cur = (cur + f[i - 1][k]) % MOD
f[i][j] = cur
}
}
}
for (let i = 0; i < 26; i++) ans = (ans + f[n][i]) % MOD
return ans
}
-
时间复杂度: ,其中 为字符集大小 -
空间复杂度:
转移优化
根据转移的依赖关系,实现上,我们并不需要真正记录每一个 ,而可以直接记录一个总的不同子序列方案数 ans。
这可以避免每次计算新状态时,都累加前一个 的值,有效减低时空复杂度。
Java 代码:
class Solution {
int MOD = (int)1e9+7;
public int distinctSubseqII(String s) {
int n = s.length(), ans = 0;
int[] f = new int[26];
for (int i = 0; i < n; i++) {
int c = s.charAt(i) - 'a', prev = f[c];
f[c] = (ans + 1) % MOD;
ans = (ans + f[c]) % MOD;
ans = (ans - prev + MOD) % MOD;
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int distinctSubseqII(string s) {
int n = s.length(), ans = 0, MOD = 1e9 + 7;
vector<int> f(26, 0);
for (int i = 0; i < n; ++i) {
int c = s[i] - 'a', prev = f[c];
f[c] = (ans + 1) % MOD;
ans = (ans + f[c]) % MOD;
ans = (ans - prev + MOD) % MOD;
}
return ans;
}
};
Python 代码:
class Solution:
def distinctSubseqII(self, s: str) -> int:
n, MOD, ans = len(s), 1e9+7, 0
f = [0] * 26
for i in range(n):
c = ord(s[i]) - ord('a')
prev = f[c]
f[c] = (ans + 1) % MOD
ans = (ans + f[c] - prev) % MOD
return int(ans)
TypeScript 代码:
function distinctSubseqII(s: string): number {
const MOD = 1e9+7
let n = s.length, ans = 0
const f = new Array<number>(26).fill(0)
for (let i = 0; i < n; i++) {
const c = s.charCodeAt(i) - 'a'.charCodeAt(0), prev = f[c]
f[c] = (ans + 1) % MOD
ans = (ans + f[c]) % MOD
ans = (ans - prev + MOD) % MOD
}
return ans
}
-
时间复杂度: -
空间复杂度:
最后
给大伙通知一下 📢 :
全网最低价 LeetCode 会员目前仍可用 ~
📅 年度会员:有效期加赠两个月!!; 季度会员:有效期加赠两周!!
🧧 年度会员:获 66.66 现金红包!!; 季度会员:获 22.22 现金红包!!
🎁 年度会员:参与当月丰厚专属实物抽奖(中奖率 > 30%)!!
专属链接:leetcode.cn/premium/?promoChannel=acoier
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
本文由 mdnice 多平台发布
相关文章:

大胆预测:计算机将要回暖
中概财报集体亮眼 虽然最近几天恒指(港股)稍有回落,但年线仍有 9% 的上涨。 过去三年,恒指分别下跌 14.08%、15.46% 和 13.82%。 而在近期,国内各大互联网都公布了财报,别看各个大厂的作妖不断,…...
49 序列化和反序列化
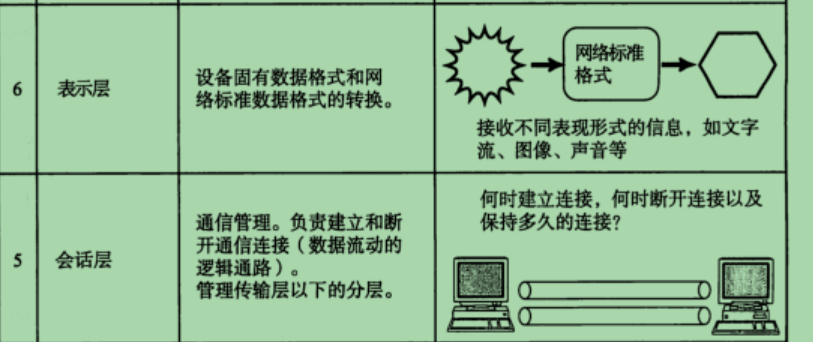
本章重点 理解应用层的作用,初识http协议 理解传输层的作用,深入理解tcp的各项特性和机制 对整个tcp/ip协议有系统的理解 对tcp/ip协议体系下的其他重要协议和技术有一定的了解 学会使用一些网络问题的工具和方法 目录 1.应用层 2.协议概念 3. 网络计…...

PS —— 精修图像
PS —— 精修图像 修复污点修复画笔工具修复画笔工具 美白滤镜去杂锐化加杂减淡和锐化工具 我觉得今天这篇博客,无论是男同胞还是女同胞,都要熟练掌握(哈哈哈哈…) 今天我们来学习如何精修图像,精修图像一般分为几步——修复&…...

哥白尼哨兵系列卫星数据不能下载的解决方法
自2023年1月24日起,一个新的哥白尼数据空间生态系统已经启动,为所有哨兵数据(Sentinel-1, Sentinel-2, Sentinel-3 and Sentinel-5P)提供可视化和数据处理,地址为:https://dataspace.copernicus.eu/。详细介…...
结构型模式之桥接模式
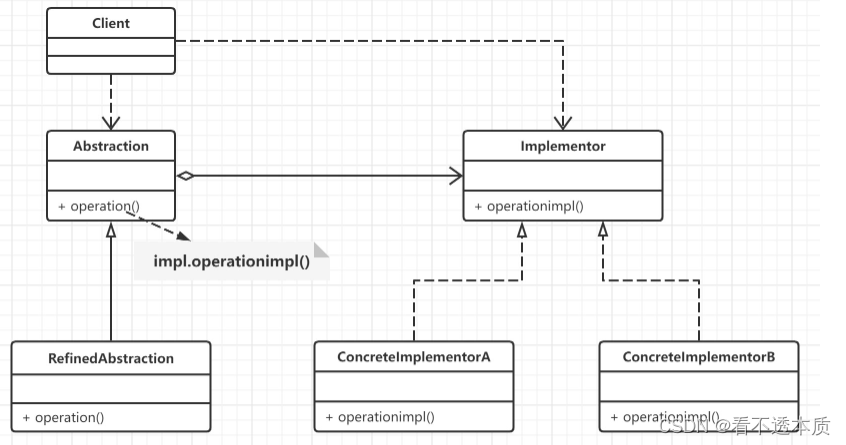
文章目录 概述原理结构图代码示例 小结 概述 桥接模式(bridge pattern) 的定义是:将抽象部分与它的实现部分分离,使它们都可以独立地变化。 桥接模式用一种巧妙的方式处理多层继承存在的问题,用抽象关联来取代传统的多层继承,将类之间的静态继承关系转…...

数据结构--顺序表
目录 1.顺序表 1.1顺序表的概念及结构 线性表 2、顺序表分类 2.1顺序表和数组的区别 静态顺序表 动态顺序表 3.顺序表的实现 3.1初始化 随后便可对顺序表初始化 3.2插入数据 尾插 头插 在指定位置插入数据 顺序表的查找 头删、尾删及指定位置删除 实现代码&#x…...

【C++项目】实时聊天的在线匹配五子棋对战游戏
目录 项目介绍 开发环境 核心技术 项目前置知识点介绍 Websocketpp 1. WebSocket基本认识 2. WebSocket协议切换原理解析 3. WebSocket报文格式 4. Websocketpp介绍 5. 搭建一个简单WebSocket服务器 JsonCpp 1. Json格式的基本认识 2. JsonCpp介绍 3. 序列化与反序…...

7.2k star的万能视频解析下载插件
今天给大家介绍一个超级厉害的浏览器插件,可以解析各个平台网页视频——猫抓。 项目简介 猫抓(cat-catch) 是一款资源嗅探扩展插件,他能够帮助你筛选列出当前页面的资源。简单来说,当你打开任意一个带有视频的网页&a…...
dmanywhere的docker制作
dmanywhere的docker制作 官网地址: http://www.dmanywhere.cn/ 下载相关执行文件。 Dockerfile的默认命名是“Dockerfile”, 在构建镜像时,如果没有指定Dockerfile文件,Docker通常会寻找名为“Dockerfile”的文件 1.Dockerf…...

Leetcode | 5-21| 每日一题
2769. 找出最大的可达成数字 考点: 暴力 数学式子计算 思维 题解 通过式子推导: 第一想法是二分确定区间在区间内进行查找是否符合条件的, 本题最关键的便是 条件确定 , 第二种方法: 一般是通过数学公式推导的,这种题目我称为数学式编程题 代码 条件判断式 class Solution {…...
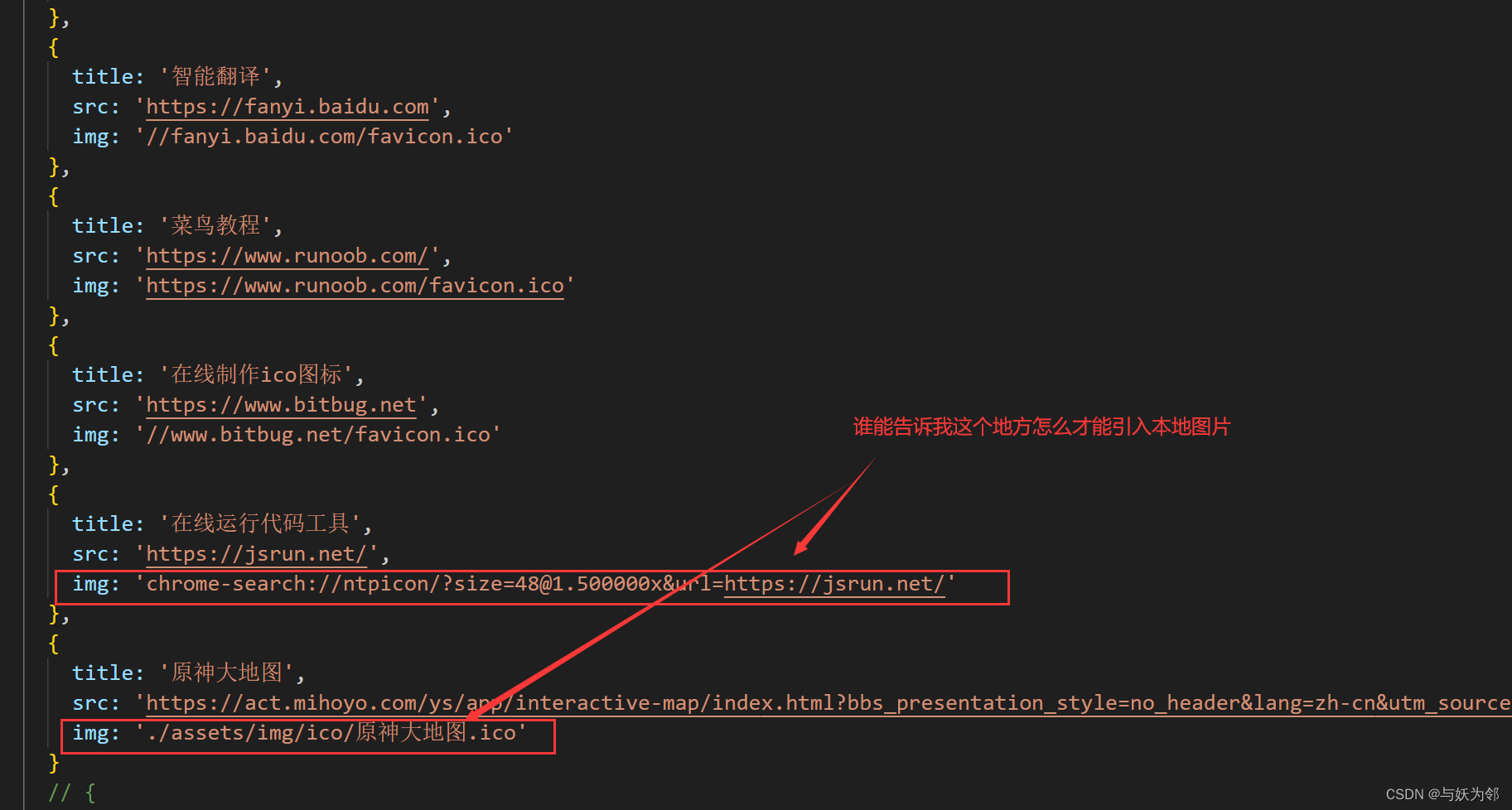
vue3添加收藏网站页面
结构与样式 <template><div class"web_view"><ul><li v-for"web in webList" :key"web.title"><a :href"web.src" :title"web.title" target"_blank"><img :src"web.img&…...

吴恩达深度学习笔记:超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter tuning)3.4-3.5
目录 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)第三周: 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架(Hyperparameter …...

牛客NC362 字典序排列【中等 DFS Java/Go/PHP】
题目 题目链接: https://www.nowcoder.com/practice/de49cf70277048518314fbdcaba9b42c 解题方法 DFS,剪枝Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回…...
、__DIR__、__FILE__的区别)
PHP获取文件路径getcwd()、__DIR__、__FILE__的区别
getcwd() getcwd() 是一个函数,它返回当前工作目录(CWD)的完整路径。当前工作目录是脚本开始执行时所在的目录,除非在脚本执行过程中通过 chdir() 函数进行了更改。 $cwd getcwd(); echo $cwd; // 输出当前工作目录的完整路径…...

Kafka(十三)监控与告警
目录 Kafka监控与告警1 解决方案1.2 基础知识JMX监控指标代理查看KafkaJMX远程端口 1.3 真实案例Kafka Exporter:PromethusPromethus Alert ManagerGrafana 1.3 实际操作部署监控和告警系统1.2.1 部署Kafka Exporter1.2.2 部署Prometheus1.2.3 部署AlertManger1.2.4 添加告警规…...

SBC3568启动升级,灵活更换动画logo
今天小智将会带着大家体验如何在openharmony sdk内替换开机logo和动态动画。 1. 更换开机logo 开机logo分为uboot阶段【logo.bmp】和kernel阶段【logo_kernel.bmp】的logo两个文件,对图片的要求是:必须为bmp格式,8或者24位深,且…...
)
v-if 与 v-show(vue3条件渲染)
v-if 是“真正”的条件渲染,因为它会确保在切换过程中条件块内的事件监听器和子组件适当地被销毁和重建。 v-if 也是惰性的:如果在初始渲染时条件为假,则什么也不做——直到条件第一次变为真时,才会开始渲染条件块。 相比之下&a…...

nuxt: generate打包后访问资源404问题
现象 使用Nuxt.js开发的个人页面,部署到nginx服务器中,/_nuxt/*.js、/_nuxt/*.css等静态问题不能访问,提示404错误。 而我们的这些资源文件是存在的。 解决方法 加上此处代码进行上下文配置 baseURL: /nuxt/ 此时在nginx配置 /nuxt 代理 lo…...
)
【图像超分】论文精读:Residual Non-local Attention Networks for Image Restoration(RNAN)
第一次来请先看这篇文章:【超分辨率(Super-Resolution)】关于【超分辨率重建】专栏的相关说明,包含专栏简介、专栏亮点、适配人群、相关说明、阅读顺序、超分理解、实现流程、研究方向、论文代码数据集汇总等) 文章目录 前言Abstract1 INTRODUCTION2 RELATED WORK3 RESIDU…...

AI大模型:大数据+大算力+强算法
前言:好久不见,甚是想念,我是辣条,我又回来啦,兄弟们,一别两年,还有多少老哥们在呢? 目录 一年半没更文我干啥去了? AI大模型火了 人工智能 大模型的理解 为什么学习…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
