【算法设计与分析】基于Go语言实现动态规划法解决TSP问题
本文针对于最近正在学习的Go语言,以及算法课实验所需内容进行Coding,一举两得!
一、前言
由于这个实验不要求向之前的实验一样做到那种连线的可视化,故可以用图形界面不那么好实现的语言进行编写,考虑到Go语言的方兴未艾,所以采用此种语言解决问题。
二、问题
TSP问题的大致解法,老师在课上已经说过了,清华大学出版社的《算法设计与分析》(第二版,然而书上伪代码存在一些疏漏)里面也有所阐述,这里不做细致解释。
三、代码分析
主要可分为三个部分,输入、输出、计算。
1.输入
输入部分需要一个整型变量存点(城市)的数量,一个矩阵存点到点的距离,另外增设一个矩阵存到某个点的最近的前驱。这里还有一个重要的问题是如何做出这些点的子集,也就是所要画的图(实验结果)的表头横向内容,代码如下:
·········var nums int// 读取二维数组的行数和列数fmt.Print("请输入(城市)点数: ")fmt.Scanln(&nums)// 初始化一个二维数组arc := make([][]int, nums)for i := range arc {arc[i] = make([]int, nums)}// 从控制台读取二维数组的值fmt.Println("请输入二维数组的元素,每行输入完毕后按回车键:")for i := 0; i < nums; i++ {for j := 0; j < nums; j++ {var putin intfmt.Scanf("%d", &putin)if putin == 0 {putin = 2004}arc[i][j] = putin}fmt.Scanln() // 跳过每行输入后的换行符}var LengthOfd int = int(math.Pow(2, float64(nums-1)))//下面的这个d就是那个动态规划法的表d := make([][]int, nums)for i := range d {d[i] = make([]int, LengthOfd)}//同样设置一个跟d一样的矩阵,来存最近的前驱front := make([][]int, nums)for i := range front {front[i] = make([]int, LengthOfd)}//初始化设置成很大的for i := range d {for j := range d[i] {d[i][j] = 2004front[i][j] = 2004}}for i := 0; i < nums; i++ {d[i][0] = arc[i][0]front[i][0] = 0}// 创建一维存所有要做子集的点。numName := make([]int, nums) //生成1,2,3for i := 1; i <= nums; i++ {numName[i-1] = i}numName = numName[:len(numName)-1]subset := subsets(numName) //生成子集sort.Slice(subset, func(i, j int) bool {return len(subset[i]) < len(subset[j])})fmt.Println(subset)
·······这里前面几个变量我不加以赘述,简单的创建和初始化(如果你用的其他语言写这道题,相信你能做到这个),这里说一下最小子集的寻找,我参考了LeetCode上一道题(力扣上的子集问题)以及CSDN上相关博主给出的解答(子集问题的GO语言其中一解,这里选择解题代码并未考虑时间及空间复杂度,大家可以试着采用leetcode上更快更好的代码),代码大意是采用了深度优先搜索的方式进行生成,下面是本题借用函数:
//来自于本站其他用户博文
func subsets(nums []int) [][]int {l := list.New()result := list.New()for i := 0; i <= len(nums); i++ {dfs(nums, 0, i, l, result)}arr := make([][]int, result.Len())k := 0for e := result.Front(); e != nil; e = e.Next(){curl := e.Value.(*list.List)arr[k] = make([]int, curl.Len())k++}i := 0;for e := result.Front(); e != nil; e = e.Next() {curl := e.Value.(*list.List)j := 0for p := curl.Front(); p != nil; p = p.Next() {arr[i][j] = p.Value.(int)j++}i++;}return arr
}func dfs(nums []int, start int, len int, l *list.List, result *list.List) {if start == len {a := list.New()for e := l.Front(); e != nil; e = e.Next() {a.PushBack(e.Value)}result.PushBack(a)return}for i := start; i < len; i++ {l.PushBack(nums[i])dfs(nums, i+1, len, l, result)b := l.Back()l.Remove(b)}
}
之后就是对得到的子集排序,因为上面代码跑出来的子集并非是有序的。

这样便得到了计算所需的所有变量。
2.计算
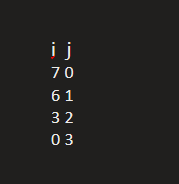
计算这个方面可以参考书中的伪代码,值得注意的是在判断大小的一些地方需要改变传参。大家可通过书中样例矩阵以及表格进行相关推导,不难发现第0列被初始化,第1到3列依靠0列更新,3到5列依靠1到3列更新,第七列特别只有第0行需要更新,而我们的最终结果需要的表格的横向表头的二维数组长这样:

所以,我们不难发现,它的长度似乎和计算有一些联系:在遍历{1}的时候,填充2和3,依靠0到1的数值,所以计算d[2][1] = arc[2][1] + d[1][0],d[3][1] = arc[3][1] + d[1][0]。依照此种规律,便可结合下文的代码内容分析:
//下面才刚刚开始tspfor j := 1; j < len(subset); j++ { //以d中的列开始扫描,也就是上面的subset(V),表头内容for i := 1; i < nums; i++ { //挨个查找看看那个数字没在V的里面,真没在就去赋值,正在查找横表头有无judge := falsefor _, theNum := range subset[j] {if theNum == i {judge = true //在的在的,就不用操作了continue}}if judge == false { //wok,真没在var edge int = 1314for _, theNum := range subset[j] { //theNum,表头中含有的内容temp := arc[i][theNum] + d[theNum][j-theNum-len(subset[j])+1]if temp < edge {edge = tempd[i][j] = edgefront[i][j] = theNum}//d[i][j] = int(math.Min(float64(d[i][j]), float64(arc[i][theNum]+d[theNum][j-1])))}}}}//求解最终结果TheLastEdge := 520for k := 1; k < nums; k++ {temp := arc[0][k] + d[k][LengthOfd-1-int(math.Pow(2, float64(k-1)))]if temp < TheLastEdge {TheLastEdge = tempd[0][LengthOfd-1] = TheLastEdgefront[0][LengthOfd-1] = k}}最后求解最后的那个框,例如本题目就是{1,2,3}下面的第0行的内容。和上面写到的,平常的点求该问题的解法如出一辙,这里并不是很好理解,计算公式甚至可以理解成是我在纯粹的找规律凑数。值得注意的是,在计算的同时front矩阵也在记录他们的上一个点(前驱),这个在后面输出发挥着重要作用。
3.输出
这里要注意以下路径是怎么打印出来的。i是直接指向最后更新的那个框框的纵坐标,j是横坐标,count用来计数确保不会在移动的途中迷路,根据书上表格,我们并不难发现下面的规律,j直接取front中的值会直接得到前驱节点的值,那么我们就应该在j行去定位这个前驱的下一个前驱,那么我们就只差寻找这个地方的纵坐标,相当巧合的是,现在的i减去现在的j的值再减去这次遍历计数器的值,正好到了我们要寻找的那个地方。(这里在草稿纸上列出我们需要加起来的点,恰好可以得出普适的规律)。
fmt.Print("TSP最短的路径是:", "0")//打印路径for i, j, count := LengthOfd-1, 0, 0; ; {j = front[j][i]i = i - j - countfmt.Print("->", j)count++if i <= 0 {fmt.Println("->0")break}}//画表for i := 0; i < len(subset); i++ {str := fmt.Sprint(subset[i])fmt.Printf("%10s", str)//fmt.Print(subset[i], "\t\t")}fmt.Println()for i := 0; i < nums; i++ {for j := 0; j < LengthOfd; j++ {bye := "-"if d[i][j] == 2004 {fmt.Printf("%10s", bye)} else {fmt.Printf("%10d", d[i][j])}}fmt.Println()}fmt.Println("最短路径是:", d[0][LengthOfd-1])大致就是这样得到了最后结果,然后再对齐一下表格。
四、代码
// TSP Problem
// Created By DDD on 2024.5.25
//package mainimport ("container/list""fmt""math""sort"
)func subsets(nums []int) [][]int {l := list.New()result := list.New()for i := 0; i <= len(nums); i++ {dfs(nums, 0, i, l, result)}arr := make([][]int, result.Len())k := 0for e := result.Front(); e != nil; e = e.Next() {curl := e.Value.(*list.List)arr[k] = make([]int, curl.Len())k++}i := 0for e := result.Front(); e != nil; e = e.Next() {curl := e.Value.(*list.List)j := 0for p := curl.Front(); p != nil; p = p.Next() {arr[i][j] = p.Value.(int)j++}i++}return arr
}func dfs(nums []int, start int, len int, l *list.List, result *list.List) {if start == len {a := list.New()for e := l.Front(); e != nil; e = e.Next() {a.PushBack(e.Value)}result.PushBack(a)return}for i := start; i < len; i++ {l.PushBack(nums[i])dfs(nums, i+1, len, l, result)b := l.Back()l.Remove(b)}
}func main() {var nums int// 读取二维数组的行数和列数fmt.Print("请输入(城市)点数: ")fmt.Scanln(&nums)// 初始化一个二维数组arc := make([][]int, nums)for i := range arc {arc[i] = make([]int, nums)}// 从控制台读取二维数组的值fmt.Println("请输入二维数组的元素,每行输入完毕后按回车键:")for i := 0; i < nums; i++ {for j := 0; j < nums; j++ {var putin intfmt.Scanf("%d", &putin)if putin == 0 {putin = 2004}arc[i][j] = putin}fmt.Scanln() // 跳过每行输入后的换行符}var LengthOfd int = int(math.Pow(2, float64(nums-1)))//下面的这个d就是那个动态规划法的表d := make([][]int, nums)for i := range d {d[i] = make([]int, LengthOfd)}//同样设置一个跟d一样的矩阵,来存最近的前驱front := make([][]int, nums)for i := range front {front[i] = make([]int, LengthOfd)}//初始化设置成很大的for i := range d {for j := range d[i] {d[i][j] = 2004front[i][j] = 2004}}for i := 0; i < nums; i++ {d[i][0] = arc[i][0]front[i][0] = 0}// 创建一维存所有要做子集的点。numName := make([]int, nums) //生成1,2,3for i := 1; i <= nums; i++ {numName[i-1] = i}numName = numName[:len(numName)-1]subset := subsets(numName) //生成子集sort.Slice(subset, func(i, j int) bool {return len(subset[i]) < len(subset[j])})fmt.Println(subset)//下面才刚刚开始tspfor j := 1; j < len(subset); j++ { //以d中的列开始扫描,也就是上面的subset(V),表头内容for i := 1; i < nums; i++ { //挨个查找看看那个数字没在V的里面,真没在就去赋值,正在查找横表头有无judge := falsefor _, theNum := range subset[j] {if theNum == i {judge = true //在的在的,就不用操作了continue}}if judge == false { //wok,真没在var edge int = 1314for _, theNum := range subset[j] { //theNum,表头中含有的内容temp := arc[i][theNum] + d[theNum][j-theNum-len(subset[j])+1]if temp < edge {edge = tempd[i][j] = edgefront[i][j] = theNum}//d[i][j] = int(math.Min(float64(d[i][j]), float64(arc[i][theNum]+d[theNum][j-1])))}}}}//求解最终结果TheLastEdge := 520for k := 1; k < nums; k++ {temp := arc[0][k] + d[k][LengthOfd-1-int(math.Pow(2, float64(k-1)))]if temp < TheLastEdge {TheLastEdge = tempd[0][LengthOfd-1] = TheLastEdgefront[0][LengthOfd-1] = k}}fmt.Print("TSP最短的路径是:", "0")//打印路径for i, j, count := LengthOfd-1, 0, 0; ; {j = front[j][i]i = i - j - countfmt.Print("->", j)count++if i <= 0 {fmt.Println("->0")break}}//画表for i := 0; i < len(subset); i++ {str := fmt.Sprint(subset[i])fmt.Printf("%10s", str)//fmt.Print(subset[i], "\t\t")}fmt.Println()for i := 0; i < nums; i++ {for j := 0; j < LengthOfd; j++ {bye := "-"if d[i][j] == 2004 {fmt.Printf("%10s", bye)} else {fmt.Printf("%10d", d[i][j])}}fmt.Println()}fmt.Println("最短路径是:", d[0][LengthOfd-1])
}/*
4
0 3 6 7
5 0 2 3
6 4 0 2
3 7 5 0
*/
五、参考文献
算法分析与设计课程实验——TSP问题与01背包问题的动态规划算法实现-CSDN博客
Go的主函数不需要写return
相关文章:

【算法设计与分析】基于Go语言实现动态规划法解决TSP问题
本文针对于最近正在学习的Go语言,以及算法课实验所需内容进行Coding,一举两得! 一、前言 由于这个实验不要求向之前的实验一样做到那种连线的可视化,故可以用图形界面不那么好实现的语言进行编写,考虑到Go语言的…...
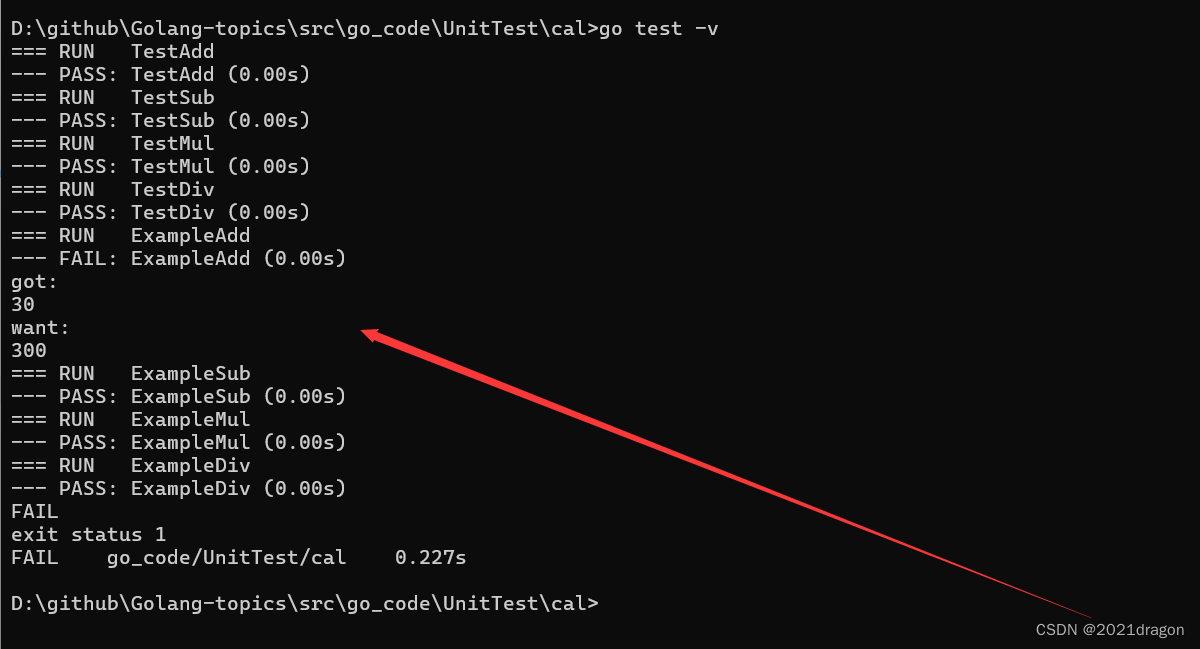
Golang单元测试
文章目录 传统测试方法基本介绍主要缺点 单元测试基本介绍测试函数基准测试示例函数 传统测试方法 基本介绍 基本介绍 代码测试是软件开发中的一项重要实践,用于验证代码的正确性、可靠性和预期行为。通过代码测试,开发者可以发现和修复潜在的错误、确保…...
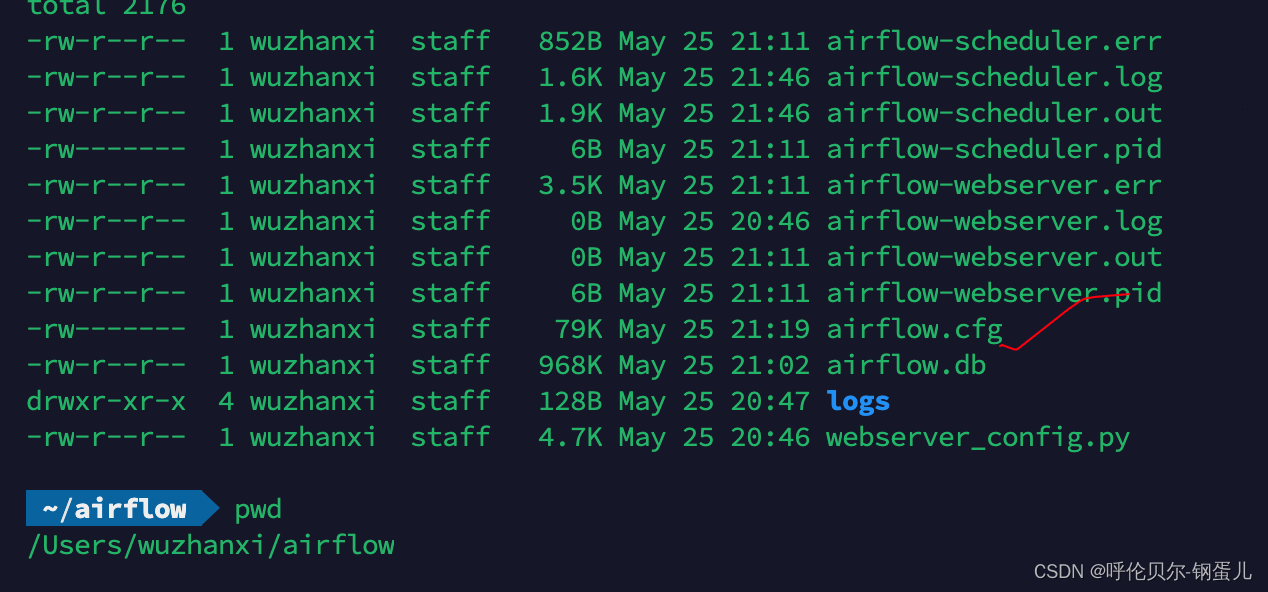
mac下安装airflow
背景:因为用的是Mac的M芯片的电脑,安装很多东西都经常报错,最近在研究怎么把大数据集群上的crontab下的任务都配置到一个可视化工具中,发现airflow好像是个不错的选择,然后就研究怎么先安装使用起来,后面再…...

二进制中1的个数c++
题目描述 计算鸭给定一个十进制非负整数 NN,求其对应 22 进制数中 11 的个数。 输入 输入包含一行,包含一个非负整数 NN。(N < 10^9) 输出 输出一行,包含一个整数,表示 NN 的 22 进制表示中 11 的个数。 样例输入 100 …...

【面试干货】数据库乐观锁,悲观锁的区别,怎么实现
【面试干货】数据库乐观锁,悲观锁的区别,怎么实现 1、乐观锁,悲观锁的区别2、总结 💖The Begin💖点点关注,收藏不迷路💖 1、乐观锁,悲观锁的区别 悲观锁(Pessimistic Lo…...
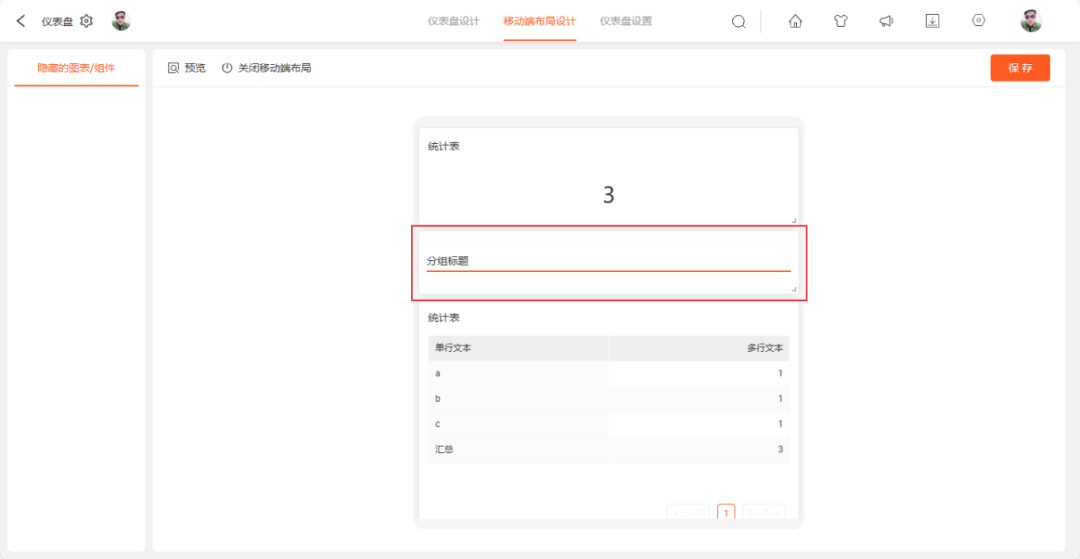
移动端仪表盘,支持更多组件
05/22 主要更新模块概览 定位函数 快捷筛选 轨迹图表 时间组件 01 表单管理 1.1 【表单组件】- 表单关联新增支持自定义按钮样式 说明: 表单关联-关联数据按钮,原仅支持默认按钮样式,现增加关联数据按钮自定义功能,满…...

科技产业园3D探秘:未来科技之城的奇幻之旅
在数字时代的浪潮中,科技产业园区成为了推动城市经济发展、科技创新的重要引擎。 当我们打开科技产业园的3D可视化模型,仿佛穿越时空,来到了一个充满奇幻色彩的科技世界。在这里,高楼大厦鳞次栉比,绿色植被点缀其间&am…...
【Python搞定车载自动化测试】——Python基于Pytest框架实现UDS诊断自动化(含Python源码)
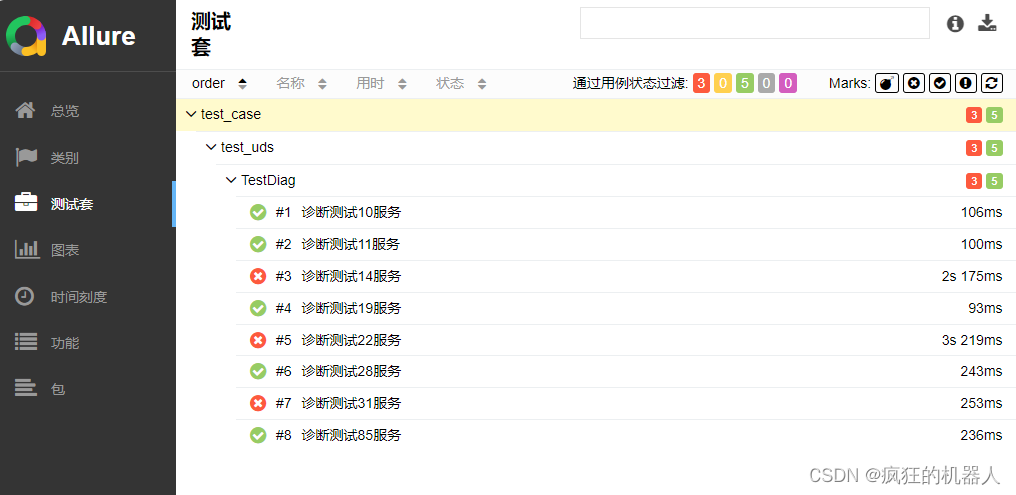
系列文章目录 【Python搞定车载自动化测试】系列文章目录汇总 文章目录 系列文章目录💯💯💯 前言💯💯💯一、环境搭建1.软件环境2.硬件环境 二、目录结构三、源码展示1.诊断基础函数方法2.诊断业务函数方法…...

探索SPI单线传输模式中时钟线与数据传输的简化
探索SPI单线传输模式:时钟线与数据传输的简化之道 在当今的嵌入式系统和微控制器通信中,串行外设接口(SPI)因其高速、全双工和同步的特点而广受欢迎。然而,随着设备尺寸和复杂性的不断减少,对SPI通信的简化…...

使用FFmpeg推流实现在B站24小时点歌直播
使用FFmpeg推流实现在B站24小时点歌直播 本文首发于个人博客 安装FFmpeg centos7 https://www.myfreax.com/how-to-install-ffmpeg-on-centos-7/ https://linuxize.com/post/how-to-install-ffmpeg-on-centos-7/ 使用FFmpeg在B站直播 https://zhuanlan.zhihu.com/p/2395…...

汽车防抱死制动系统ABS的单片机程序Proteus仿真设计
次设计对汽车防抱死系统进行简单的设计,针对车速、轮速两个信号进行分析,并根据最佳滑移率计算。采用对比实时滑移率对比分析,ECU控制制动器进行制动力调节使滑移率在制动过程处于最佳范围,保证系统具有良好制动性能。 汽车的制动液压调节器主要包含以下几个部件:调压电磁…...
IOS开发者证书快捷申请
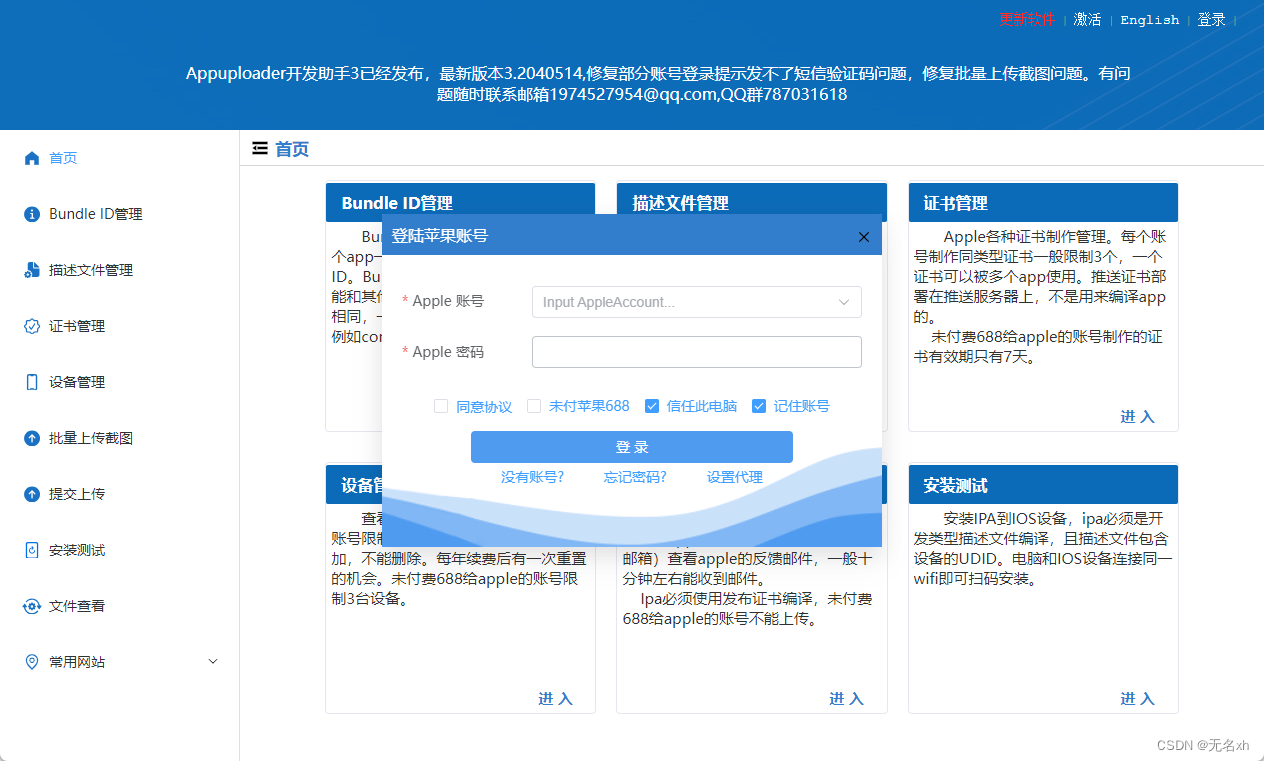
App Uploader 在进行iOS应用开发中,可以借助appuploader辅助工具进行证书制作、上传和安装测试等操作。首先,您需要访问官方网站获取最新版本的appuploader。最新版本已经优化了与Apple账号的登录流程,无需支付688元,并提供了Windows版和Mac版供用户选择。下载完成后,解压…...

python 火焰检测
在日常生活,总是离不开火,有时候我们需要预防火灾发生,但是我们又不可能一直盯着,这时候我们就需要一款程序帮我们盯着,一旦发生火灾从而告知我们,今天就带大家编写这么一款应用。 安装需要的库 pip install opencv-python 代码实现 import cv2 # Library for…...

栈——顺序存储
#include<stdio.h> #define MaxSize 10 //栈的所有操作时间复杂度都是O(1) //定义 typedef struct{int data[MaxSize];int top; //栈顶指针,永远指向栈顶元素 }SqStack;//初始化,使栈顶指针指向-1 void InitStack(SqStack &S){S.top-1; }…...
军队仓库管理系统|DW-S301系统特点
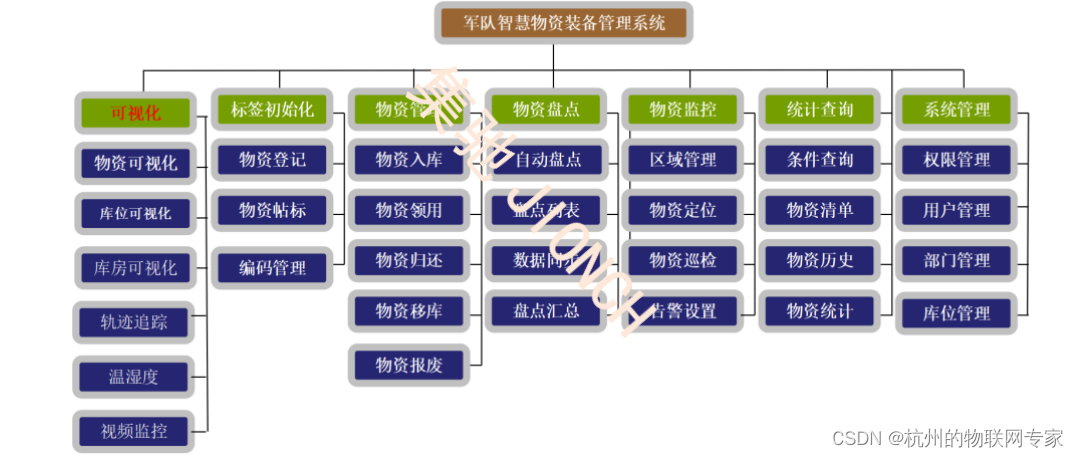
部队仓库管理系统DW-S301系统通过数据采集、互联网和物联网技术,实现数字化智能管控,以提高军用物资的仓储准确率和流转率,缩短周转时间,降低库存成本,也有助于消除生产过程中的不确定性。 系统功能:通过部…...

MySQL和MongoDB数据库的区别
MySQL和MongoDB数据库的区别 随着大数据和云计算技术的兴起,数据库的选择成为开发者和架构师必须面对的重要决策。MySQL和MongoDB作为关系型数据库和非关系型数据库的代表,在各自领域都有着广泛的应用。本文将从多方面详细比较MySQL和MongoDB࿰…...

类脑计算和量子计算、人工智能的关系
According to www.iAsk.ai Ask Ai Search Engine: 类脑计算、量子计算和人工智能是三个不同但相关的领域。它们在不同层面上探索和利用了不同的计算模型和技术,但都旨在推动计算能力的发展和创新。 类脑计算是一种受到人脑神经系统启发的计算模型。它试图通过模拟…...
Qt5 互动地图,实现无人机地面站效果
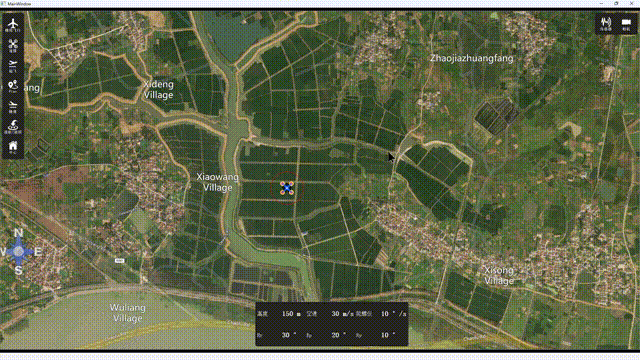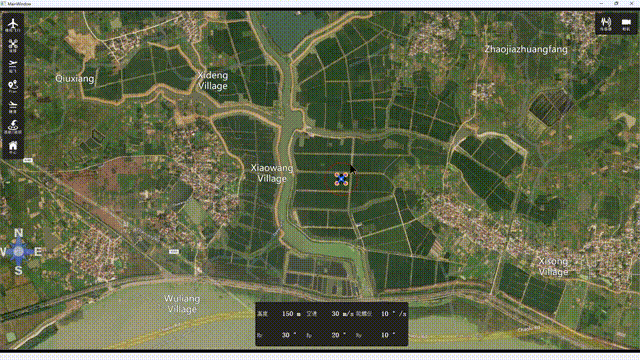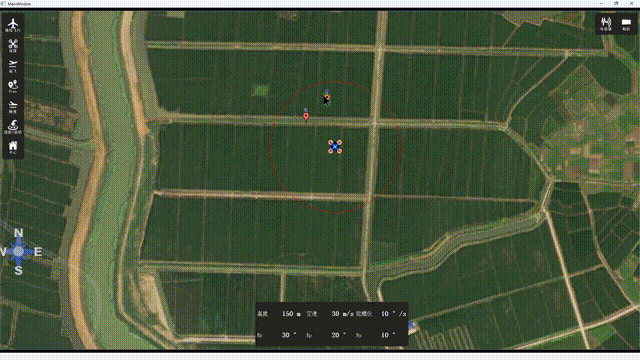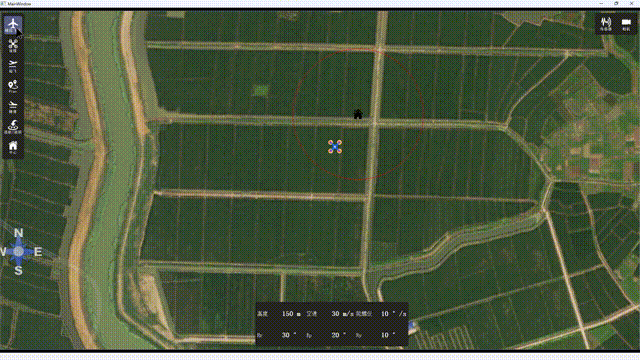
一、概述 本文主要通过Qt5opmapcontrol实现一个简单的无人机地面站效果。opmapcontrol是一个比较古老的QT开源地面站库,可选择谷歌地图,必应地图, 雅虎地图,GIS等。可直接使用源码,也可以编译生成库进行调用。实现效果…...

【文末附gpt升级方案】TikTok Symphony AI套件:智能视频制作的新篇章
TikTok Symphony AI套件:智能视频制作的新篇章 摘要 随着短视频平台的兴起,视频内容的创作与制作已成为品牌方吸引用户、传递信息的重要手段。TikTok作为全球领先的短视频平台,近日宣布推出Symphony AI套件,旨在通过人工智能技术…...

面试回答——有高并发、高性能、高可用系统架构设计实践以及性能调优经验
🌈hello,你好鸭,我是Ethan,一名不断学习的码农,很高兴你能来阅读。 ✔️目前博客主要更新Java系列、项目案例、计算机必学四件套等。 🏃人生之义,在于追求,不在成败,勤通…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
