网络空间安全数学基础·整除与同余
主要内容:
整除的基本概念(掌握)
素数(掌握)
同余的概念(掌握)
1.1整除
定义:设a,b是任意两个整数,其中b≠0,如果存在一个整数q,使 a = qb,则我们称b整除a,或a被b整除,记为b|a,此时称 b是a的因子,a是b的倍数。
例:a=10, b=2则有2|10;若a=100, b=10有10|100
例:设a是整数,a≠0, 则a|0。
整除的基本性质:
1. 如果b|a且a|b,则b = a或b = -a。
2. 如果a|b且b|c,则a|c。
3. 如果c|a且c|b,则c|ua+vb,其中u,v是整数。
整除的基本性质(补充):
(1) a|b<=>-a|b<=>a|-b<=>-a|-b<=>|a| | |b|
(2) b≠0且a|b => |a|≤|b|
带余除法:当两个整数不能整除时,我们有带余除法:
定义:对于a,b两个整数,其中b≠0,则存在唯一q,r使得:a=bq+r,0 ≤ r<|b|。r称为a被b除得到的余数, 当r = 0时,b|a。
例:
1)a = –37, b= 5,则–37 = (-8)×5+3,q=8,r=3
2)a = 67,b= 7,则67=(9)×(7)+4,q=9, r=4
最大公因子:
定义:
1) 设a,b是两个整数,如果整数c|a且c|b,则c称为a,b的公因子。
2) 设c>0是两个不全为零的整数a,b的公因子,如果a,b的任何公因子都整除c,则c称为a,b的最大公因子,记为c=(a,b)。
最大公因子性质:
1.(a,b)=(-a,b)=(a,-b)=(-a,-b)=(|a|,|b|)
2.(0,a)=a
最大公因子(求解)
例:(-3824,1837)
最大公因子定理:
定理:设a,b是两个不全为零的整数,则存在两个整数u, v,使得:(a, b)=ua+vb。
例:将a = 888,b = 312的最大公因子表示为(a,b) = ua+vb。
1.2互素
定义:设a,b是两个不全为0的整数,如果(a, b)=1,则称a,b互素。
推论:a, b互素的充分必要条件是:存在u,v,使ua+vb=1。
互素性质:
1) 如果c|ab且(c, a) = 1,则c|b 。
2) 如果a|c,b|c,且(a, b) = 1,则ab|c 。
3) 如果(a,c) = 1,(b,c) = 1,则(ab,c) =1 。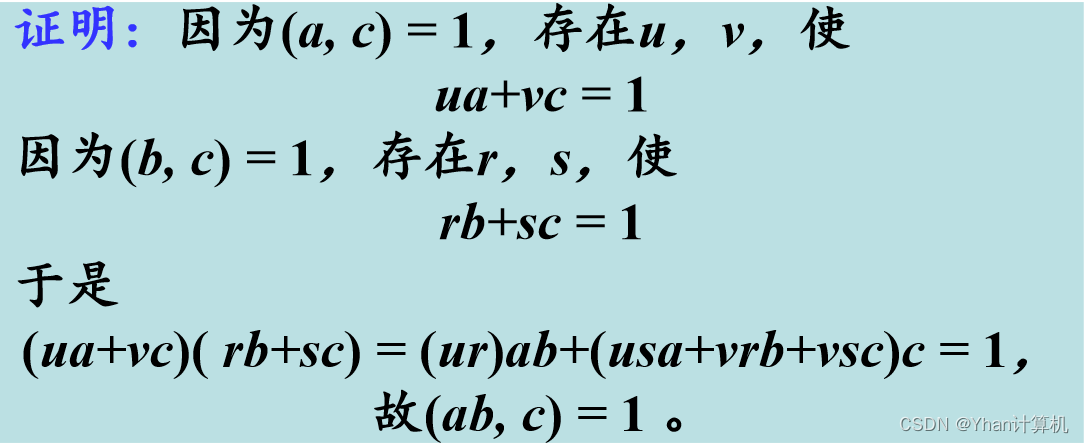
最小公倍数:
定义:
1) 设a, b是两个不等于零的整数.如果a|d,b|d,则称d是a和b的公倍数。
2) a和b的正公倍数中最小的称为a和b的最小公倍数,记为[a,b] 。
最小公倍数性质:
[a,b] = [–a,b] = [a,–b] = [–a,–b] = [|a|,|b|]
例:a = 2,b = 3.它们的公倍数集合为{0,±6,±12,±18,…}.而[2,3] = 6 。
最小公倍数与最大公因子关系:
定理:
1) 设d是a,b的任意公倍数,则[a, b] | d 。
2)![]() ,特别地,如果(a, b) = 1, [a, b] = |ab|。
,特别地,如果(a, b) = 1, [a, b] = |ab|。
1.3素数
定义:如果一个大于1的整数p除±1和±p外无其他因子,则p称为一个素数,否则称为合数。
定理:设p是一个素数,则
1) 对任意整数a,如果p不整除a,则(p,a) = 1。
2) 如果p|ab,则p|a,或p|b。
算术基本定理:
定理:每个大于1的整数a都可以分解为有限个素数的乘积:a=p1p2…pr。该分解除素数因子的排列外是唯一的。
标准因子分解式:
由于p1,p2,…,pr中可能存在重复,所以a的分解式可表示为有限个素数的幂的乘积:![]() ,这称为a的标准因子分解式。
,这称为a的标准因子分解式。
例:2100的标准因子分解式:
素数无穷个:
定理:素数有无穷多个。
Eratosthenes筛法:
定理:设a是任意大于1的整数,则a的除1外最小正因子q是一素数,并且当a是一合数时,![]() 。
。
对于一般N,Eratosthenes筛法可表述如下:
第1步 找出的全部![]() 素数:p1,p2,…,pm。
素数:p1,p2,…,pm。
第2步 在1~N中分别划去p1,p2,…,pm全部倍数。
第2步完成后剩下的数除1外就是不超过N的全部素数。
筛法原理如下:对于一个数a≤N,如果p1,p2,…,pm都不整除a,则a是素数。这是因为如果a是合数,则由定理它必有一素因子在p1,p2,…,pm中。
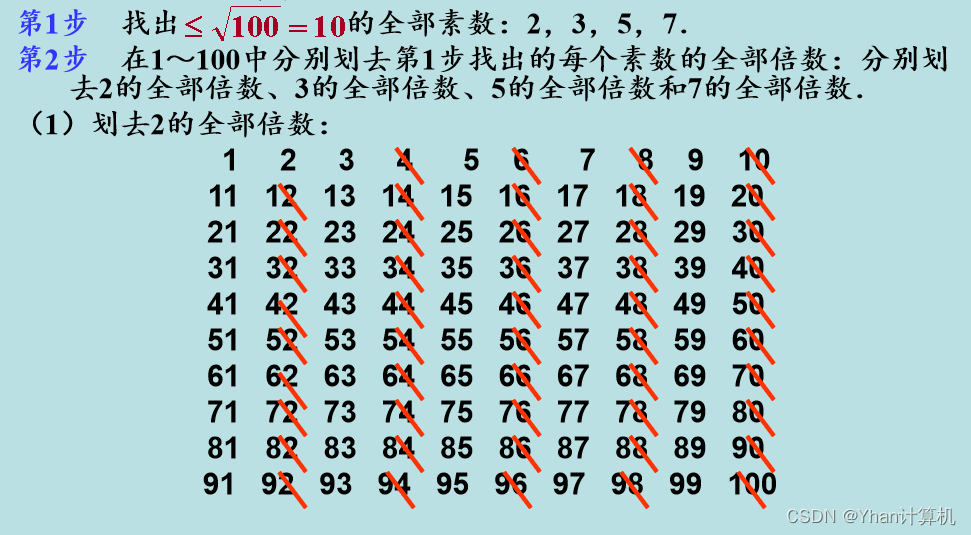
例:求不超过100的全部素数。
同理可以将因子5,7的倍数划去: (3) 划去5的全部倍数: (4) 划去7的全部倍数。
最终经过上述步骤后剩下的数除1外就是不超过100的全部素 数: (25个) 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
1.4 同余
定义:给定一个称为模的正整数m。如果m除整数a,b得相同的余数,即a=q1m+r,b=q2m+r,0≤ r小于等于m, 则称a和b关于模m同余,记为 a≡b (mod m)
例:25≡1(mod 8),16≡-5(mod 7)。
定理:整数a,b对模m同余的充分必要条件是:m|(a-b),即a = b+mt,t是整数。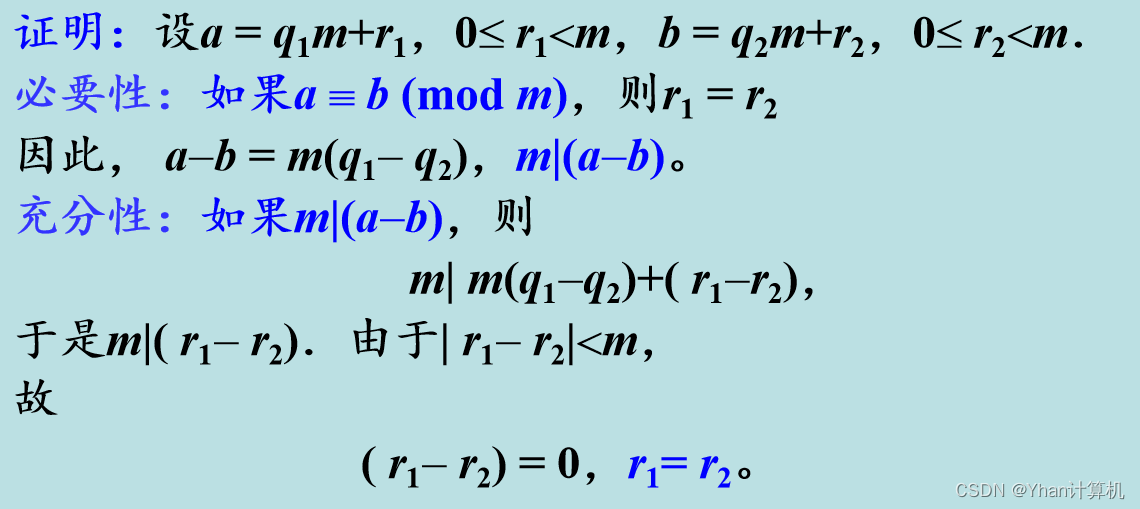
同余性质及推论:
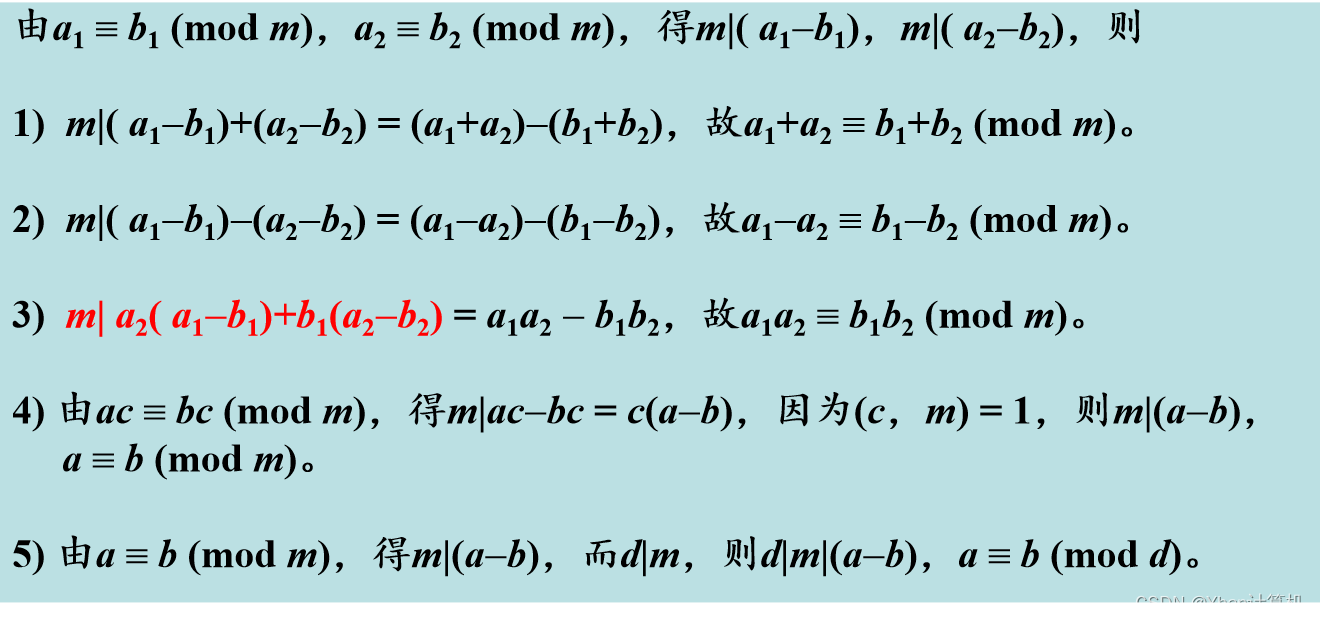
推论:如果a1≡b1 (mod m),a2≡b2 (mod m),则:
快速指数算法
例1-16:求解 2^64 (mod 641)
相关文章:

网络空间安全数学基础·整除与同余
主要内容: 整除的基本概念(掌握) 素数(掌握) 同余的概念(掌握) 1.1整除 定义:设a,b是任意两个整数,其中b≠0,如果存在一个整数q,使 …...

同旺科技 FLUKE ADPT 隔离版发布 ---- 说明书
所需设备: 1、FLUKE ADPT 隔离版 内附链接; 应用于:福禄克Fluke 12E / 15BMax / 17B Max / 101 / 106 / 107 应用于:福禄克Fluke 15B / 17B / 18B...
)
云计算-角色、特性和模型 (Roles, Characteristics, and Models)
角色、特性和模型 (Roles, Characteristics, and Models) 角色和边界 (Roles and Boundaries) 为了识别云计算模型,我们首先需要了解各种参与者的角色和边界。由于云系统通常遵循面向服务的模型,我们需要了解服务提供者和服务订阅者之间的边界。我们将遵…...

介绍一下Hugging Face,这个公司的背景是什么
Hugging Face是一家成立于2016年的人工智能公司,专注于为AI研究人员和开发者提供开源模型库和工具。以下是关于Hugging Face公司的详细背景介绍: 公司历史与创始人: Hugging Face由Clment Delangue、Julien Chaumond和Thomas Wolf三位法国籍…...
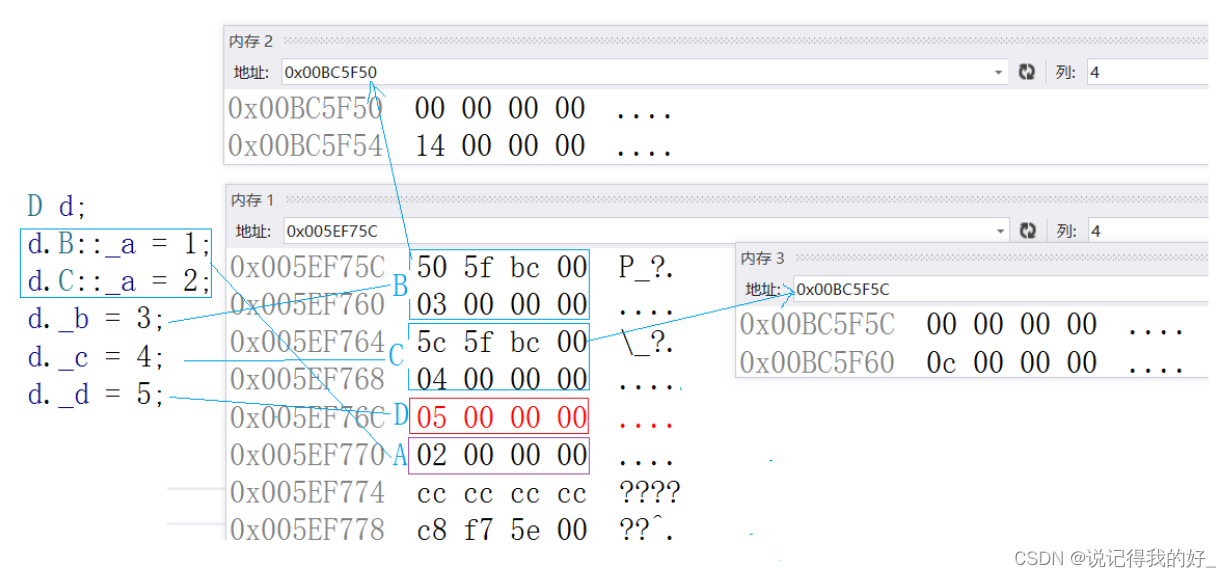
【C++高阶(一)】继承
目录 一、继承的概念 1.继承的基本概念 2.继承的定义和语法 3.继承基类成员访问方式的变化 编辑 4.总结 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 1.派生类中的默认构造函数 2.派生类中的拷贝构造函数 3.派生类中的移动构造函数…...

AI原生嵌入式矢量模型数据库ChromaDB-部署与使用指南
在人工智能大模型领域, 离不开NLP技术,在NLP中词向量是一种基本元素,如何存储这些元素呢? 可以使用向量数据库ChromeDB Chroma Chroma 是 AI 原生开源矢量数据库。Chroma 通过为 LLM 提供知识、事实和技能,使构建 L…...
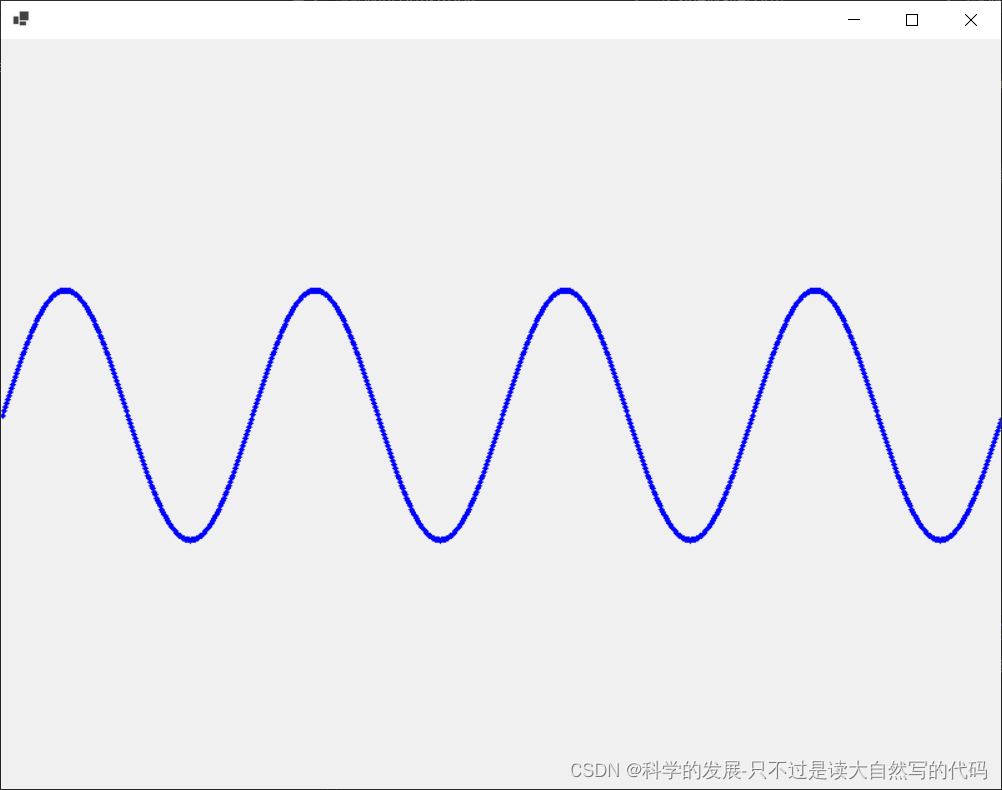
c# 画一个正弦函数
1.概要 c# 画一个正弦函数 2.代码 using System; using System.Drawing; using System.Windows.Forms;public class SineWaveForm : Form {private const int Width 800;private const int Height 600;private const double Amplitude 100.0;private const double Period…...
Docker学习(3):镜像使用
当运行容器时,使用的镜像如果在本地中不存在,docker 就会自动从 docker 镜像仓库中下载,默认是从 Docker Hub 公共镜像源下载。 一、列出镜像列表 可以使用 docker images 来列出本地主机上的镜像。 各个选项说明: REPOSITORY&am…...
【Git】版本控制工具——Git介绍及使用
目录 版本控制版本控制系统的主要目标分类小结 分布式版本控制系统——GitGit特点Git与SVN的区别Git的工作机制 Git安装Git 团队协作机制团队内协作跨团队协作远程仓库远程仓库的作用有以下几个方面远程仓库操作流程/团队协作流程 Git分支什么是分支分支的好处 Git的常用命令Gi…...
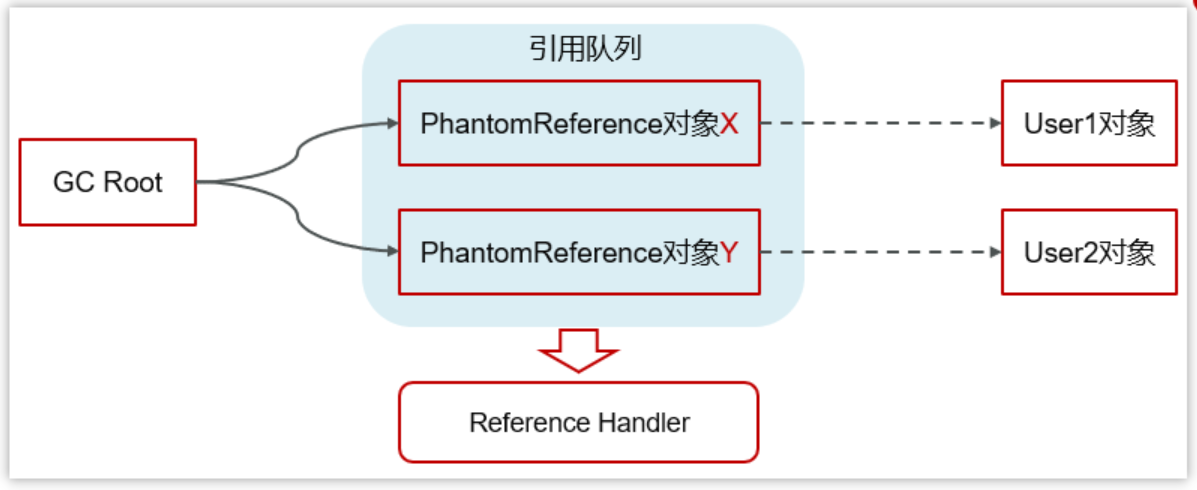
面试八股之JVM篇3.6——垃圾回收——强引用、弱引用、虚引用、软引用
🌈hello,你好鸭,我是Ethan,一名不断学习的码农,很高兴你能来阅读。 ✔️目前博客主要更新Java系列、项目案例、计算机必学四件套等。 🏃人生之义,在于追求,不在成败,勤通…...

博客摘录「 Sql Server 收缩日志文件原理及always on 下的实践」2024年5月22日
四、Always on 环境下实践 先对数据库进行完整备份: EXEC sp_configure show advanced options, 1; RECONFIGURE; EXEC sp_configure xp_cmdshell, 1; RECONFIGURE; DECLARE DbName NVARCHAR(1000); DECLARE myCursor CURSOR LOCAL STATIC FOR S…...
——StringBuffer操作)
每日一题(5)——StringBuffer操作
编写程序,对StringBuffer对象进行追加,插入和修改缓冲区长度等操作; class StringDemo{public static void main(String[] args){boolean btrue;int i321;long l123456;String s1new String("Hello,world!");StringBuffer s2new S…...

默认路由实现两个网段互通实验
默认路由实现两个网段互通实验 **默认路由:**是一种特殊的静态路由,当路由表中与数据包目的地址没有匹配的表项时,数据包将根据默认路由条目进行转发。默认路由在某些时候是非常有效的,例如在末梢网络中,默认路由可以…...
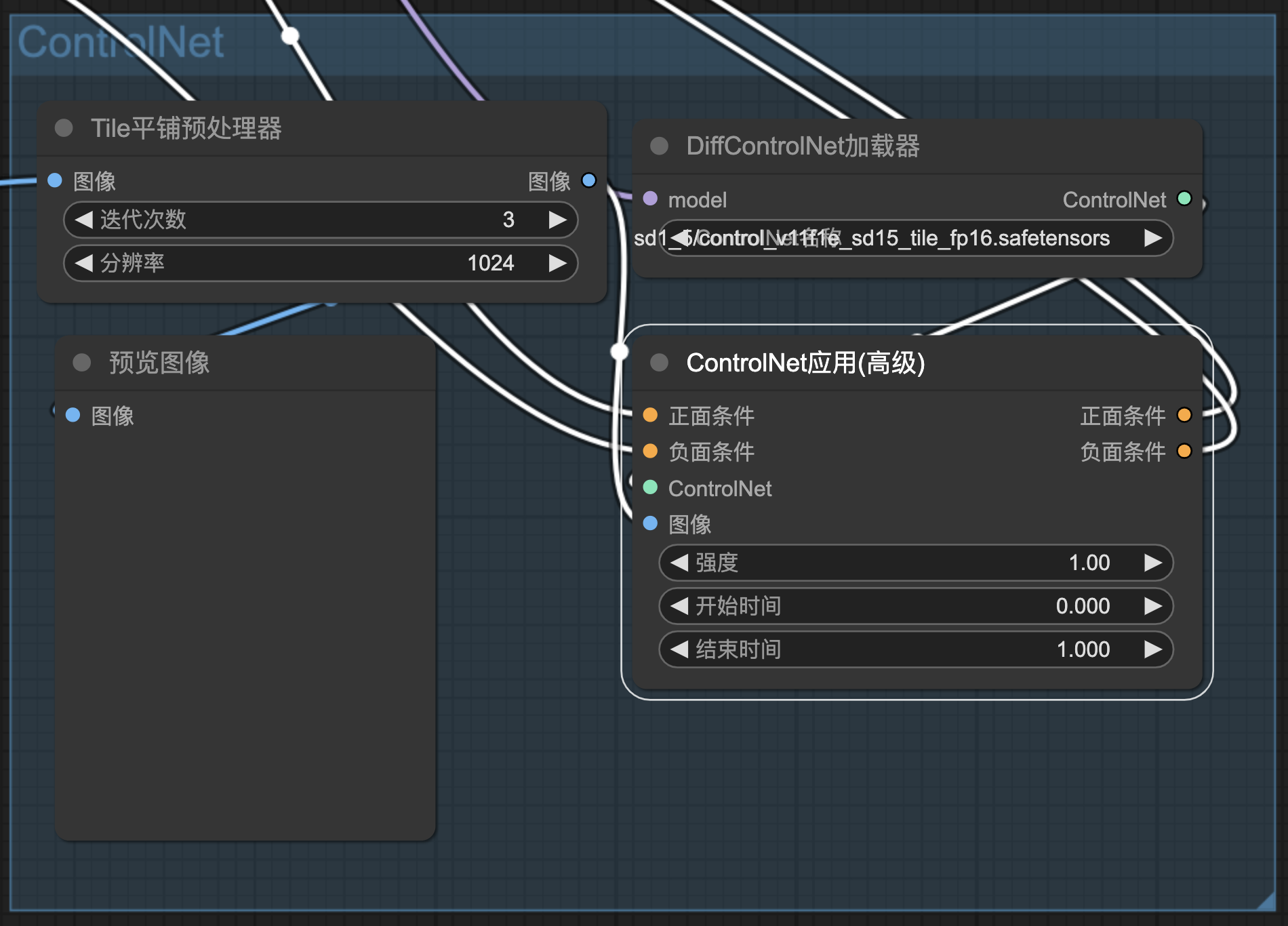
ComfyUI完全入门:图生图局部重绘
大家好,我是每天分享AI应用的萤火君! 这篇文章的主题和美女有关,不过并不是教大家生产美女视频,而是讲解 ComfyUI 的图生图局部重绘,其中将会以美女图片为例,来展示局部重绘的强大威力。 先看看效果&…...

基于UDP的网络多人聊天室
UDP服务器 #include <myheader.h>//宏定义打印错误信息 #define PRINT_ERR(msg) \do \{ \printf("%S,%D,%S\n",__FI…...

美国FDA认证是什么,食品FDA注册申请流程
美国FDA认证是什么? 美国FDA认证,全称为美国食品药品监督管理局(Food and Drug Administration)的认证,是美国政府为了确保食品、药品、医疗器械等产品的安全性和有效性所设立的重要制度。FDA认证的种类繁多&#x…...

golang的context和chan 的使用
1. context 作用 context包的context的接口,主要是控制协程执行上下文的时间,以及取消程序的执行,以及上下文中传递数据等作用,golang中耗时或者需要协同的操作都会见到context的身影。 context有几个常用的方法 1.1 context.B…...
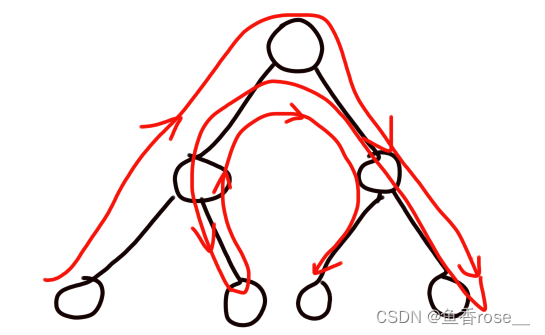
洛谷P3574 [POI2014] FAR-FarmCraft(树形dp)
洛谷 P 3574 [ P O I 2014 ] F A R − F a r m C r a f t (树形 d p ) \Huge{洛谷P3574 [POI2014] FAR-FarmCraft(树形dp)} 洛谷P3574[POI2014]FAR−FarmCraft(树形dp) 文章目录 题意题目说明 思路标程 题目…...
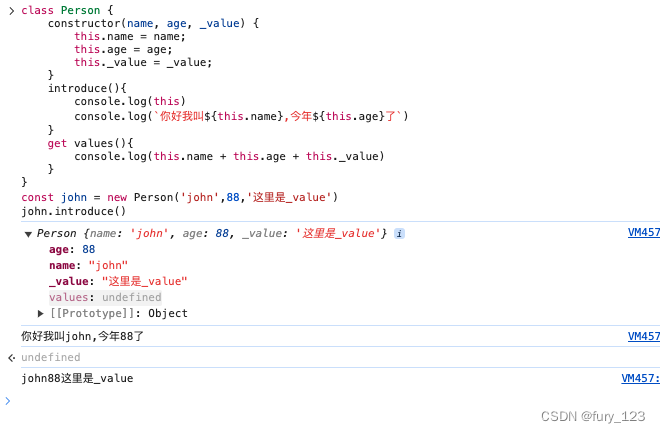
vue/core源码中ref源码的js化
起源: 当看见reactivity文件中的ref.ts文件长达五百多的ts代码后,突发奇想想看下转化成js有多少行。 进行转化: let shouldTrack true; // Define shouldTrack variable let activeEffect null; // Define activeEffect variable// 定义…...

准备打ccf
准备打ccf...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...