洛谷P3574 [POI2014] FAR-FarmCraft(树形dp)
洛谷 P 3574 [ P O I 2014 ] F A R − F a r m C r a f t (树形 d p ) \Huge{洛谷P3574 [POI2014] FAR-FarmCraft(树形dp)} 洛谷P3574[POI2014]FAR−FarmCraft(树形dp)
文章目录
- 题意
- 题目说明
- 思路
- 标程
题目链接:P3574 [POI2014] FAR-FarmCraft - 洛谷
题意
给出 n n n个节点、 n − 1 n-1 n−1条边的一棵无根树;经过每条边所用时间都为 1 1 1。然后每个节点都有点权 b [ i ] b[i] b[i]。
题目故事:管理员从自己家(一号节点)出发,然后将一批电脑分发给每个节点的居民,每个居民得到电脑后会立即开始下载游戏,下载游戏的时间为点权 b [ i ] b[i] b[i]。
管理员每次经过某节点就相当于直接分发给居民。
管理员的车恰好能够走每条路两遍。
要求计算出管理员从开始配送到所有居民都能玩上游戏所用最少时间。
题目说明
给一棵树,走过每条边需要花费一个时间,安装软件又需要花费一个时间,需要遍历整棵树并回到起点,想让所有点中到达时间+安装时间的最大值最小,问这个值是多少?
思路
跟据题目要求,显然能够知道,题目要求求出所有居民中最后玩上游戏的居民所用时间,并且要求这个时间最小。
跟据题目说明,我们可以想到:对于同一个节点的子节点,大致的贪心思路是先遍历点权最大的节点。
但是可能会出现一种情况(画的比较丑陋,多多见谅):
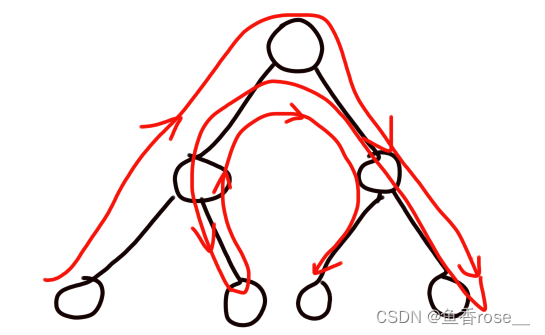
但是我们可以注意到题目有限制条件**“管理员的车恰好能够走每条路两遍”**,那么我们就不用考虑这种情况了。
一般地,我们用 f [ i ] f[i] f[i]表示节点 i i i这棵子树中的最大值, d e p [ i ] dep[i] dep[i]表示从节点 i i i出发遍历其子树并返回所用的总时间, b [ i ] b[i] b[i]表示点权。
容易发现,这道题属于树形dp中的选择节点型,只不过需要判断的是选择子节点的先后顺序。
那么对应的状态转移方程即为:
f [ x ] = max ( f [ x ] , d e p [ x ] + max ( f [ i ] , f [ j ] + d e p [ i ] + 2 ) + 1 ) f[x]=\max(f[x], dep[x]+\max(f[i],f[j]+dep[i]+2)+1) f[x]=max(f[x],dep[x]+max(f[i],f[j]+dep[i]+2)+1)
其中 x x x为当前节点, i , j i,j i,j表示它的其中两个子节点。需要解释一下:
- 方程中的
+2是因为从一个子节点到另一个子节点的两段路。 - 方程中的
+1是因为从 x x x节点到子节点的一段路。
但是该这样进行状态转移,我们需要对子节点相互比较,其时间复杂度为 O ( n 2 ) O(n^2) O(n2),会超时。
我们考虑优化状态转移方程:
-
如果先 i i i后 j j j: max ( f [ i ] , f [ j ] + d e p [ i ] + 2 ) \max(f[i],f[j]+dep[i]+2) max(f[i],f[j]+dep[i]+2)
-
如果先 j j j后 i i i: max ( f [ j ] , f [ i ] + d e p [ j ] + 2 ) \max(f[j],f[i]+dep[j]+2) max(f[j],f[i]+dep[j]+2)
-
因为 f [ i ] < f [ i ] + d e p [ j ] + 2 f[i] <f[i]+dep[j]+2 f[i]<f[i]+dep[j]+2且 f [ j ] < f [ j ] + d e p [ i ] + 2 f[j]<f[j]+dep[i]+2 f[j]<f[j]+dep[i]+2
-
原式可化为: max ( f [ j ] + d e p [ i ] + 2 , f [ i ] + d e p [ j ] + 2 ) \max(f[j]+dep[i]+2,f[i]+dep[j]+2) max(f[j]+dep[i]+2,f[i]+dep[j]+2)
-
即为: f [ i ] − d e p [ i ] < f [ j ] − d e p [ j ] f[i]-dep[i]<f[j]-dep[j] f[i]−dep[i]<f[j]−dep[j](当选 j j j时成立)
因此在判断选取子节点时,可以先对子节点按照上述不等式排序,即为选取子节点的先后顺序。
最后需要注意的是,dfs过程中我们并没有判断根节点的时间,需要输出时进行判断取 m a x max max。
标程
#include<bits/stdc++.h>using namespace std;#define IOS ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
#define int long long
#define ULL unsigned long long
#define PII pair<int, int>
#define lowbit(x) (x & -x)
#define Mid ((l + r) >> 1)
#define ALL(x) x.begin(), x.end()
#define endl '\n'
#define fi first
#define se secondconst int INF = 0x7fffffff;
const int Mod = 1e9 + 7;
const int N = 5e5 + 10;int n;
vector<int> a[N];
int b[N], dep[N], f[N];void dfs(int x, int y) {if(x != 1) f[x] = b[x];for(auto i : a[x]) {if(i == y) continue;dfs(i, x);}sort(ALL(a[x]), [](int n1, int n2) {return dep[n1] - f[n1] < dep[n2] - f[n2];});for(auto i : a[x]) {if(i == y) continue;f[x] = max(f[x], f[i] + dep[x] + 1);dep[x] += dep[i] + 2;}
}void Solved() {cin >> n;for(int i = 1; i <= n; i ++ ) {cin >> b[i];}for(int i = 1; i < n; i ++ ) {int x, y; cin >> x >> y;a[x].push_back(y); a[y].push_back(x);}dfs(1, 0);cout << max(f[1], dep[1] + b[1]) << endl;
}signed main(void) {IOSint ALL = 1; // cin >> ALL;while(ALL -- ) Solved();// cout << fixed;//强制以小数形式显示// cout << setprecision(N); //保留n位小数return 0;
}
相关文章:

洛谷P3574 [POI2014] FAR-FarmCraft(树形dp)
洛谷 P 3574 [ P O I 2014 ] F A R − F a r m C r a f t (树形 d p ) \Huge{洛谷P3574 [POI2014] FAR-FarmCraft(树形dp)} 洛谷P3574[POI2014]FAR−FarmCraft(树形dp) 文章目录 题意题目说明 思路标程 题目…...
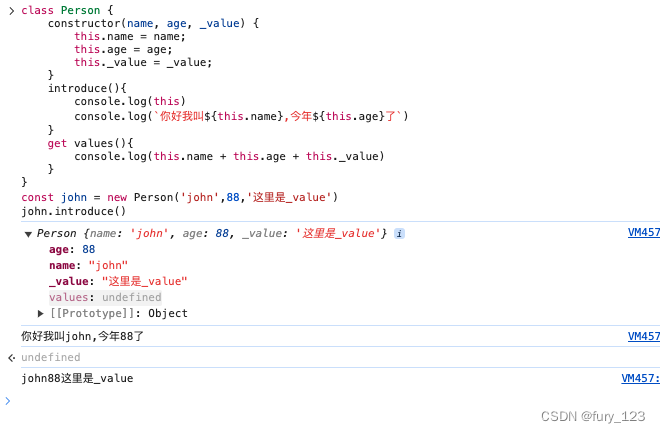
vue/core源码中ref源码的js化
起源: 当看见reactivity文件中的ref.ts文件长达五百多的ts代码后,突发奇想想看下转化成js有多少行。 进行转化: let shouldTrack true; // Define shouldTrack variable let activeEffect null; // Define activeEffect variable// 定义…...

准备打ccf
准备打ccf...

k8s遇到的错误记录
时隔四年有开始重新鼓捣k8s了,重新安装后遇到的错误记录如下: Error: Package: kubelet-1.14.0-0.x86_64 (kubernetes) Requires: kubernetes-cni 0.7.5 Available: kubernetes-cni-0.3.0.1-0.07a8a2.x86_64 (kubernetes) …...
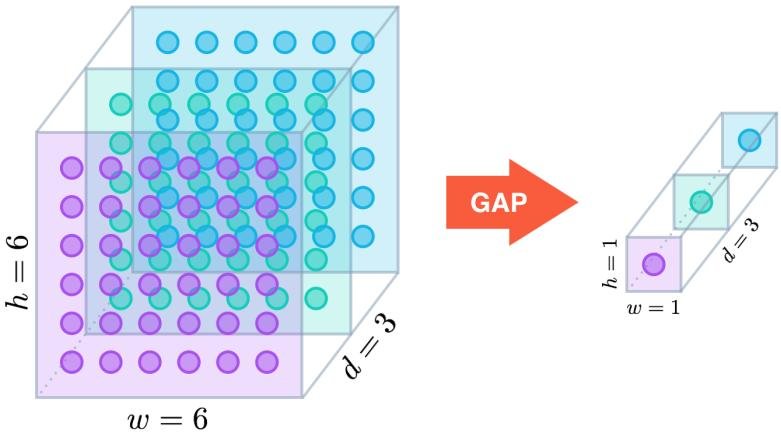
全局平均池化笔记
全局平均池化(Global Average Pooling, GAP)是一种用于卷积神经网络(CNN)中的池化操作,其主要作用和优点包括: 减少参数数量:全局平均池化层将每个特征图通过取其所有元素的平均值,压…...
)
【数仓系列】maxcompute、postgresql、sparksql等行转列数据处理实战总结(其他类型持续总结更新)
1.熟悉、梳理、总结项目研发实战中的SQL开发日常使用中的问题、经验总结,都是常用的开发技能,可以省去很多时间,时间长就忘记了 2.欢迎点赞、关注、批评、指正,互三走起来,小手动起来! 文章目录 1.maxcompu…...

用数据,简单点!奇点云2024 StartDT Day数智科技大会,直播见
在充满挑战的2024,企业如何以最小化的资源投入和试错成本,挖掘新的增长机会,实现确定性发展? “简单点”是当前商业环境的应对策略,也是奇点云2024 StartDT Day的核心理念。 5月28日,由奇点云主办的2024 S…...
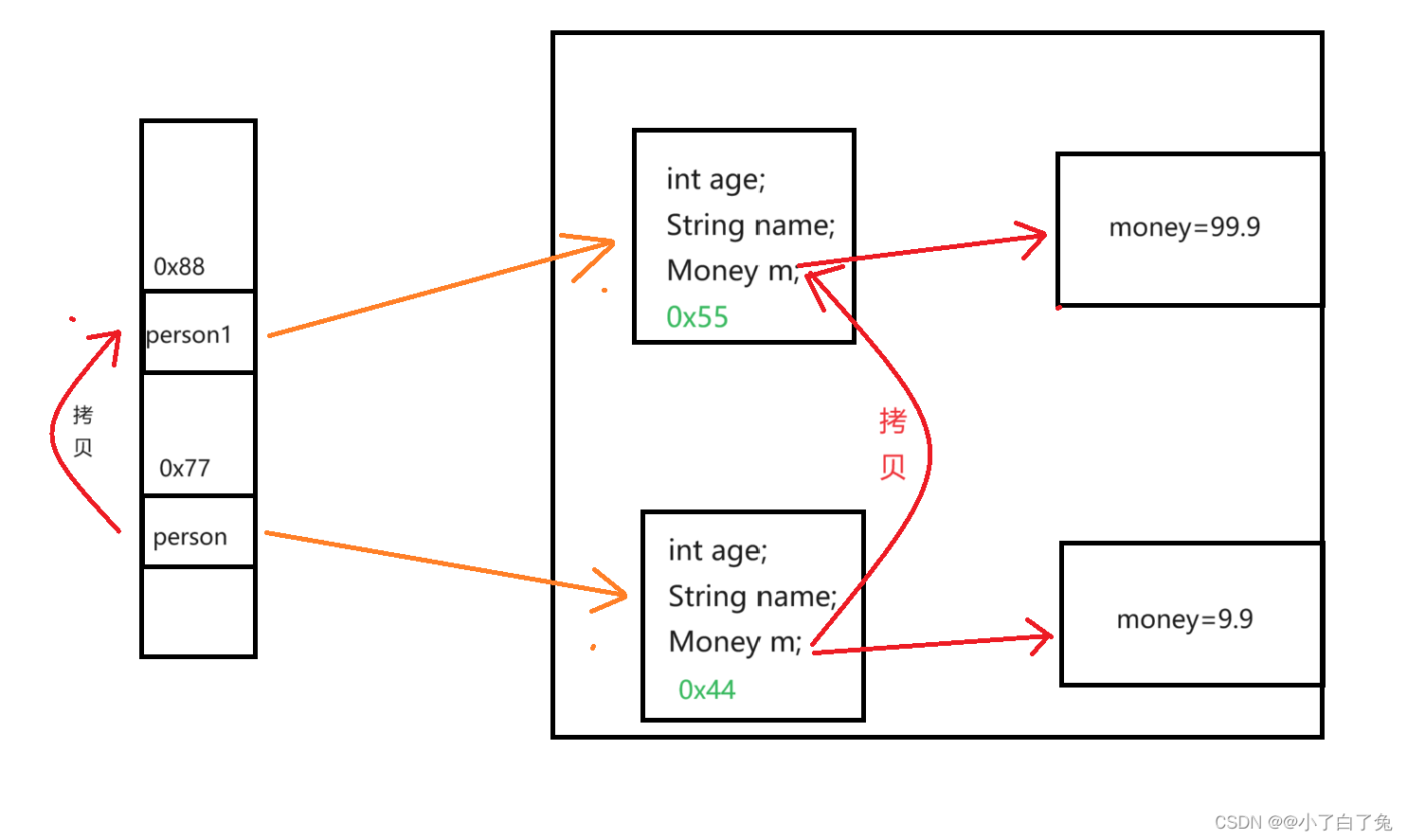
Cloneable接口和深拷贝
在java中如何对对象进行拷贝呢?我们可以使用Object类中的clone方法。 一、浅拷贝 在使用clone方法对对象进行拷贝的时候,需要注意: 1.需要重写clone方法; 2.clone方法的返回值是Object类,需要强制类型转化…...
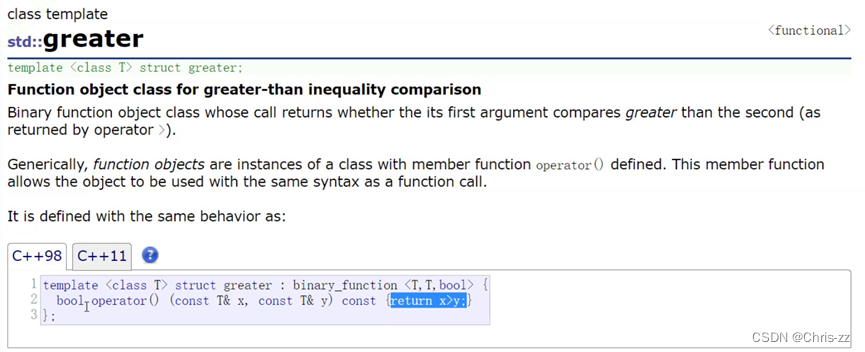
C++:vector的介绍及使用
✨✨✨学习的道路很枯燥,希望我们能并肩走下来! 文章目录 文章目录 前言 一、vector的介绍 二、vector的使用 2.1.构造和赋值重载(Member functions) 2.2 vector iterator 的使用 2.3 vector 空间增长问题 2.4 vector 增删查改 三 sort 四 v…...

【机器学习】大模型在机器学习中的应用:从深度学习到生成式人工智能的演进
🔒文章目录: 💥1.引言 ☔2.大模型概述 🚲3.大模型在深度学习中的应用 🛴4.大模型在生成式人工智能中的应用 👊5.大模型的挑战与未来展望 💥1.引言 随着数据量的爆炸性增长和计算能力的提…...
营销短信XML接口对接发送示例
在现代社会中,通信技术日新月异,其中,短信作为一种快速、简便的通信方式,仍然在日常生活中占据着重要的地位。为了满足各种应用场景的需求,短信接口应运而生,成为了实现高能有效通信的关键。 短信接口是一种…...

【C语言刷题系列】求一个数组中两个元素a和b的和最接近整数m
💓 博客主页:倔强的石头的CSDN主页 📝Gitee主页:倔强的石头的gitee主页 ⏩ 文章专栏:C语言刷题系列 目录 一、问题描述 二、解题思路 解题思路: 解题步骤: 三、C语言代码实现及测试 一、问题描述 给定一…...

Python pdf2imges -- pdf文件转图片
pdf文件转图片,需要安装PyMuPDF包,具体PyMuPDF包介绍可以参考:Python 处理 PDF 的神器 -- PyMuPDF import fitz # pip install PyMuPDF# PDF转换为IMG统一管理 def pdf_to_images(pdf_path, img_path, filename):"""pdf_p…...

分布式版本控制工具 git
git 是什么 分布式版本控制工具。github 是代码托管平台。 git 有什么用 保存文件的所有修改记录。使用版本号(sha1 哈希值) 进行区分。随时可浏览历史版本记录。可还原到历史指定版本。对比不同版本的文件差异。 为什么要使用 git 多人协作开发一个大…...

Flutter 中的 ExpansionTile 小部件:全面指南
Flutter 中的 ExpansionTile 小部件:全面指南 在 Flutter 应用中,ExpansionTile 是一个常用的折叠列表项,它允许用户点击标题来展开或折叠更多的内容。这个组件在实现可折叠列表、FAQ 部分或显示详情信息时非常有用。本文将详细介绍 Expansi…...

二进制的协议的测试程序
一、引子 由于要调试二进制私有协议,不想用C重头到尾写,用C写工程量有点大,因此想找一个比较简单的工具,postman无法实现,外界的几乎找不到合适的工具,只能考虑手写一个。 前面写了一个python通过tcp协议发…...

多线程事务
一、业务场景 我们在工作中经常会到往数据库里插入大量数据的工作,但是既需要保证数据的一致性,又要保证程序执行的效率。因此需要在多线程中使用事务,这样既可以保证数据的一致性,又能保证程序的执行效率。但是spring自带的Trans…...
春秋云境CVE-2020-26048
简介 CuppaCMS是一套内容管理系统(CMS)。 CuppaCMS 2019-11-12之前版本存在安全漏洞,攻击者可利用该漏洞在图像扩展内上传恶意文件,通过使用文件管理器提供的重命名函数的自定义请求,可以将图像扩展修改为PHP…...
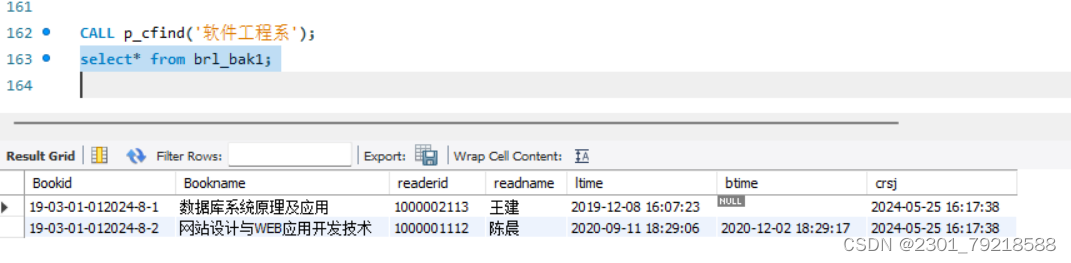
MySQL 带游标的存储过程(实验报告)
一、实验名称: 带游标的存储过程 二、实验日期: 2024 年 5月 25 日 三、实验目的: 掌握MySQL带游标的存储过程的创建及调用; 四、实验用的仪器和材料: 硬件:PC电脑一台; 配置࿱…...
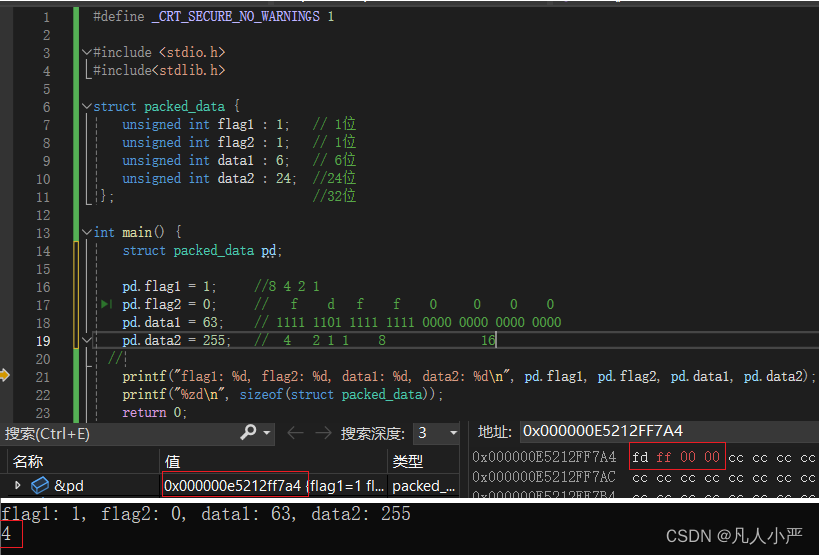
结构体(位段)内存分配
结构体由多个数据类型的成员组成。那编译器分配的内存是不是所有成员的字节数总和呢? 首先,stu的内存大小并不为29个字节,即证明结构体内存不是所有成员的字节数和。 其次,stu成员中sex的内存位置不在21,即可推测…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
