java - 数据结构,算法,排序
一、概念
1.1、排序
排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
平时的上下文中,如果提到排序,通常指的是排升序(非降序)。 通常意义上的排序,都是指的原地排序(in place sort)
原地排序:就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
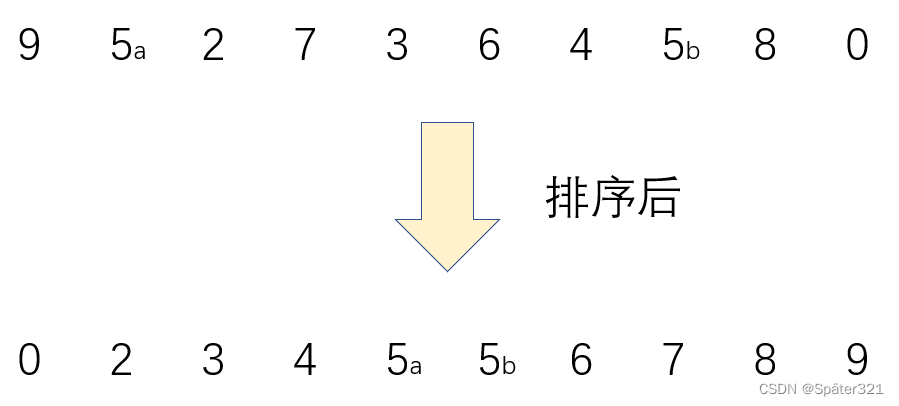
1.2、稳定性(重要)
两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法
1.3、应用
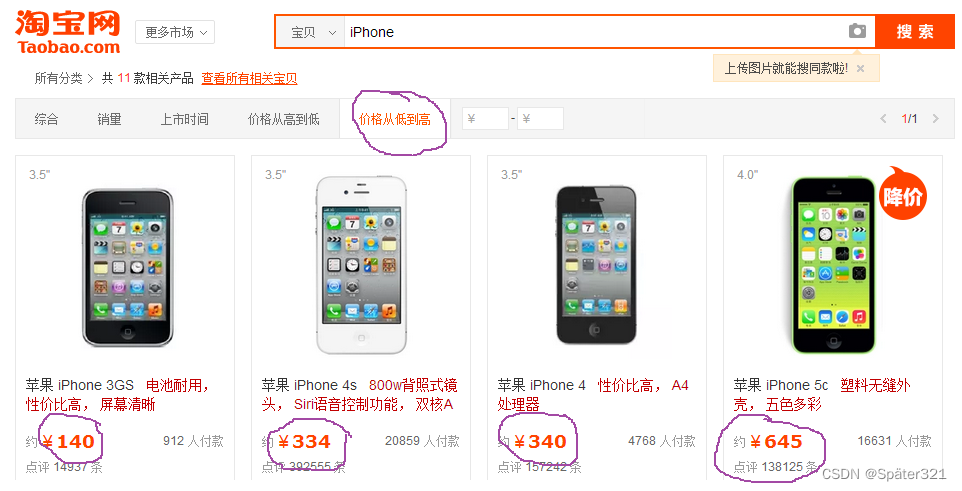
1. 各大商城的价格从低到高等
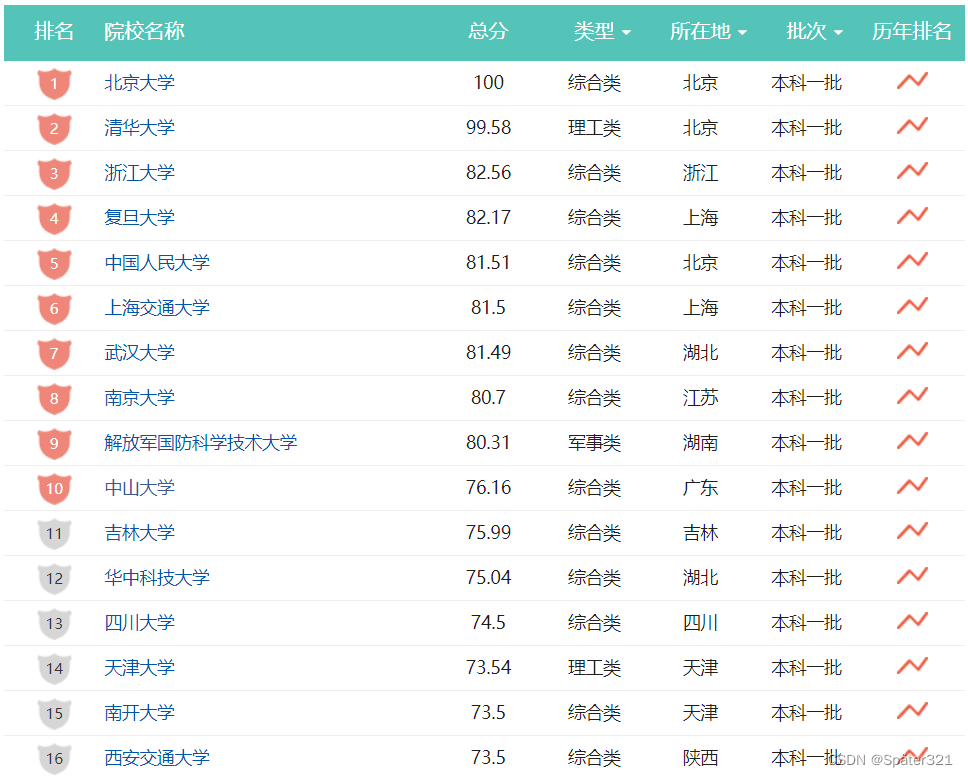
2. 中国大学排名
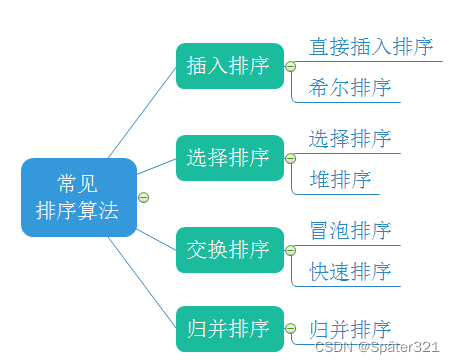
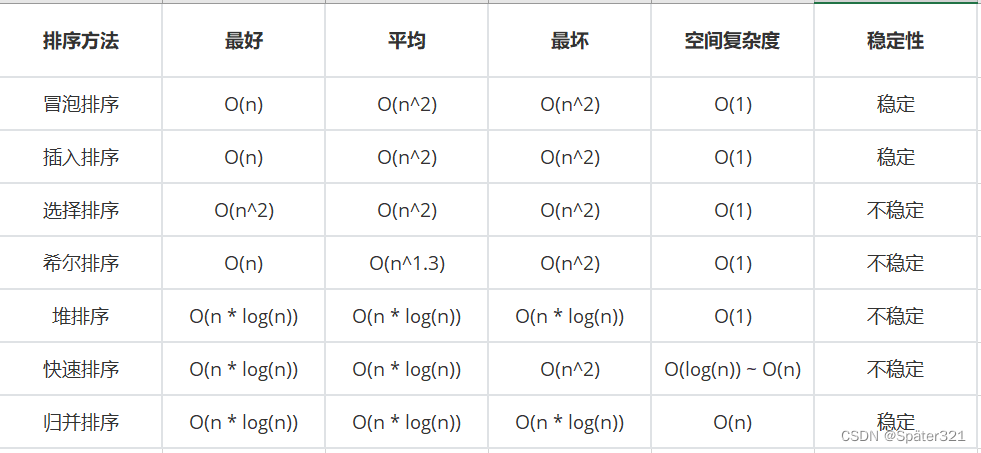
二、七大基于比较的排序-总览
三、插入排序
3.1、直接插入排序-原理
整个区间被分为
- 有序区间
- 无序区间
每次选择无序区间的第一个元素,在有序区间内选择合适的位置插入
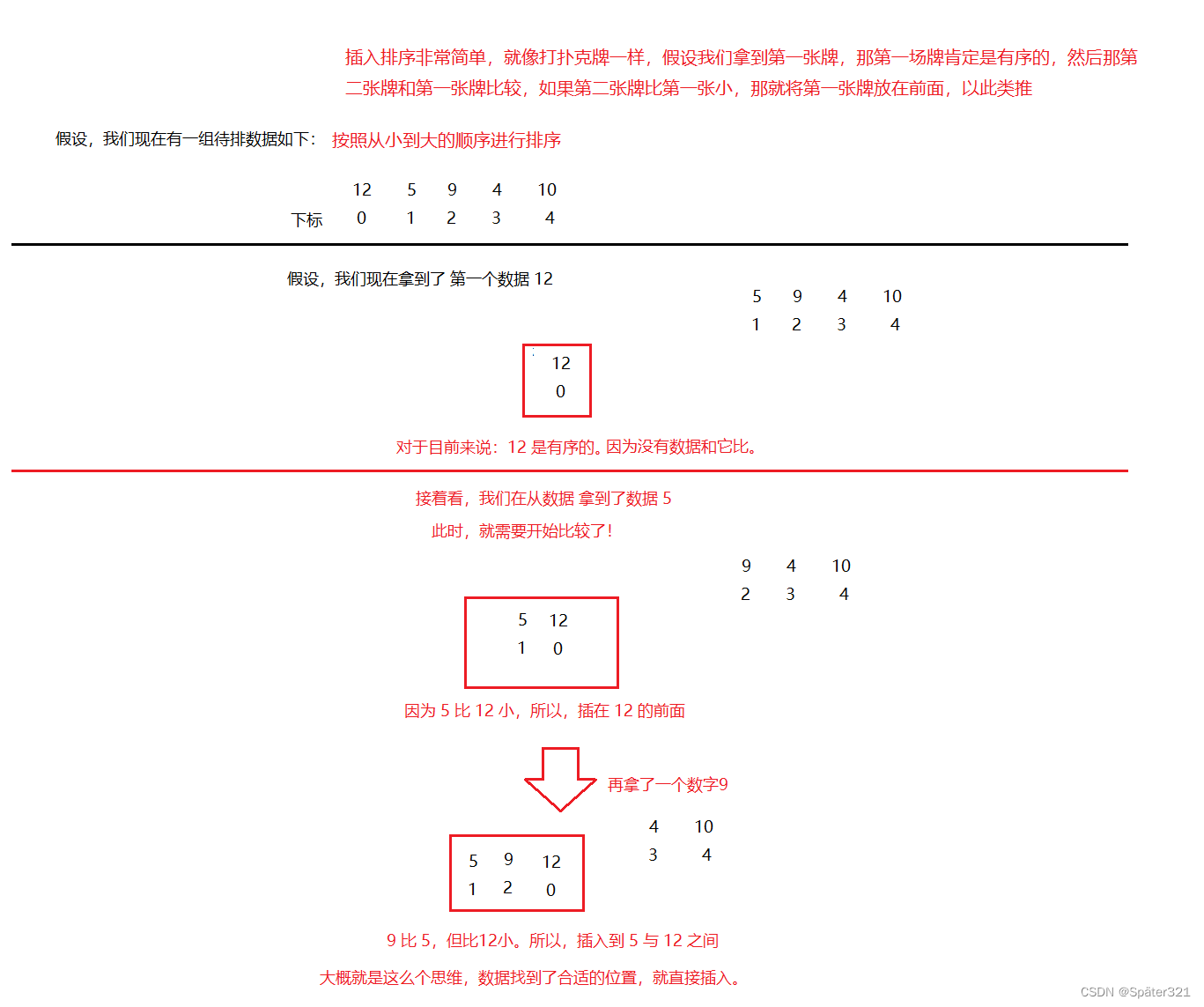
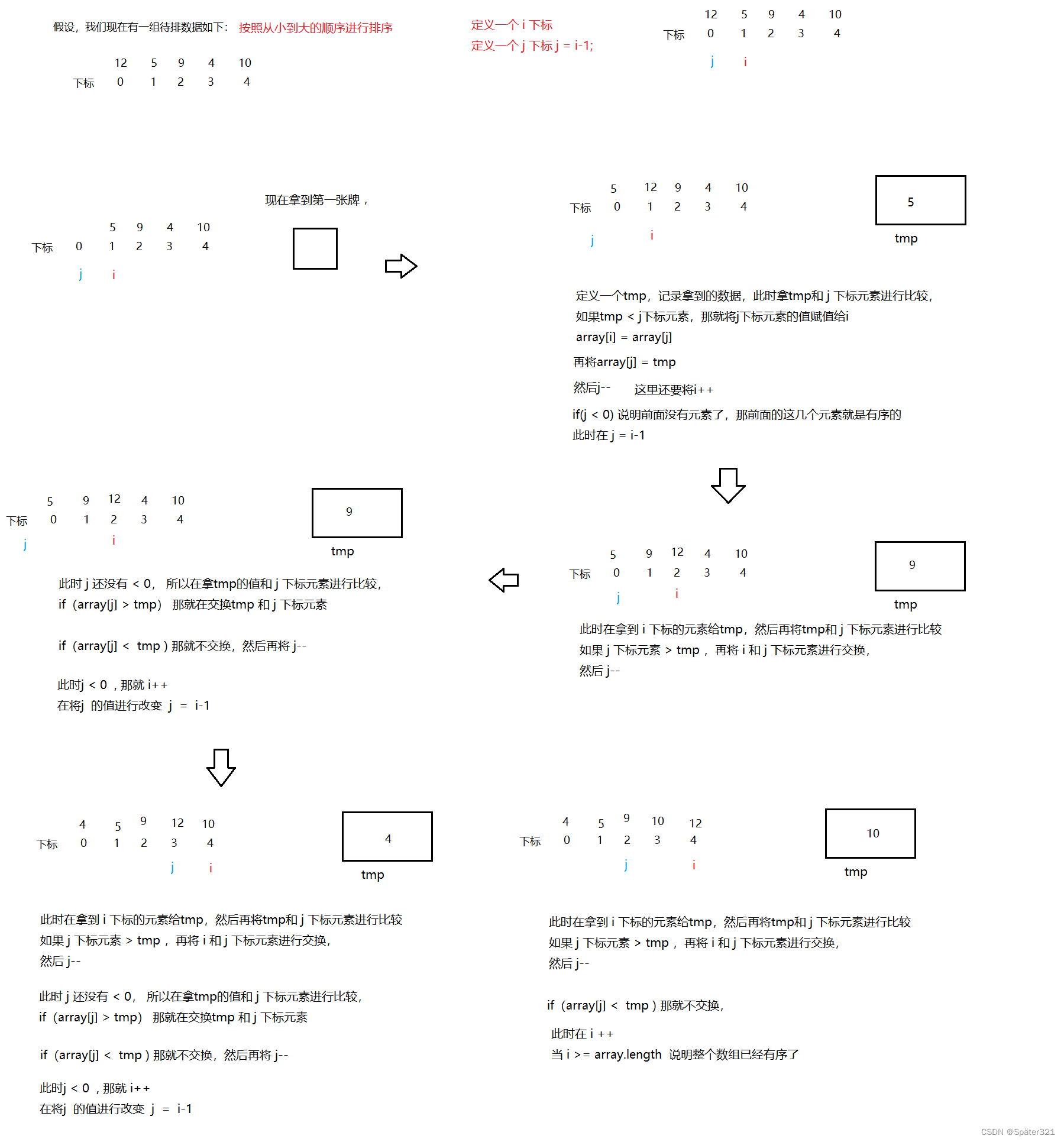
插入排序非常简单,就像打扑克牌一样,假设我们拿到第一张牌,那第一场牌肯定是有序的,然后那第二张牌和第一张牌比较,如果第二张牌比第一张小,那就将第一张牌放在前面,以此类推
根据这个思维:第一个数据是有序的,也就是说:在我们遍历的时候,是从下标1 开始的。
具体的操作见下图:
3.2、实现直接插入排序
/*** 直接插入排序,按照从小到达的循序* @param array*/public static void insertSortUp(int[] array){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for ( ;j >= 0; j--) {if(array[j] > tmp){array[j+1] = array[j];}else {break;}}array[j+1] = tmp;}}
3.3、插入排序的性能分析
插入排序的稳定性:

结论
一个稳定的排序,可以实现为 不稳定的排序。 但是,一个本身就不稳定的排序是 无法变成 稳定的排序。
直接插入排序 是 有序的。 它的时间复杂度是 O(N^2);最好情况:O(N【数组有序】 也就是说:对于直接插入排序,数据越有序越快!
由此,不难联想到:直接插入排序有时候 会用于 优化 排序。
【假设:假设我们有一百万个数据需要排序,在排序的过程中,区间越来越小,数据越来越有序。直接插入排序的时间复杂度为 O(N),N
越来越小,那么,使用 直接插入排序是不是越来越快!也就是说:直接插入排序 有时候会 用于 排序优化】 直接插入排序经常使用在
数据量不多,且整体数据趋于有序的。
四、希尔排序
4.1、原理
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数n,把待排序文件中所有记录分成n个组,所有距离为 (数据量/n) 的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达只有一个组时,所有记录在统一组内排好序。
- 希尔排序是对直接插入排序的优化。
- 当gap > 1(gap就是要分成的组数)时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很
快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比
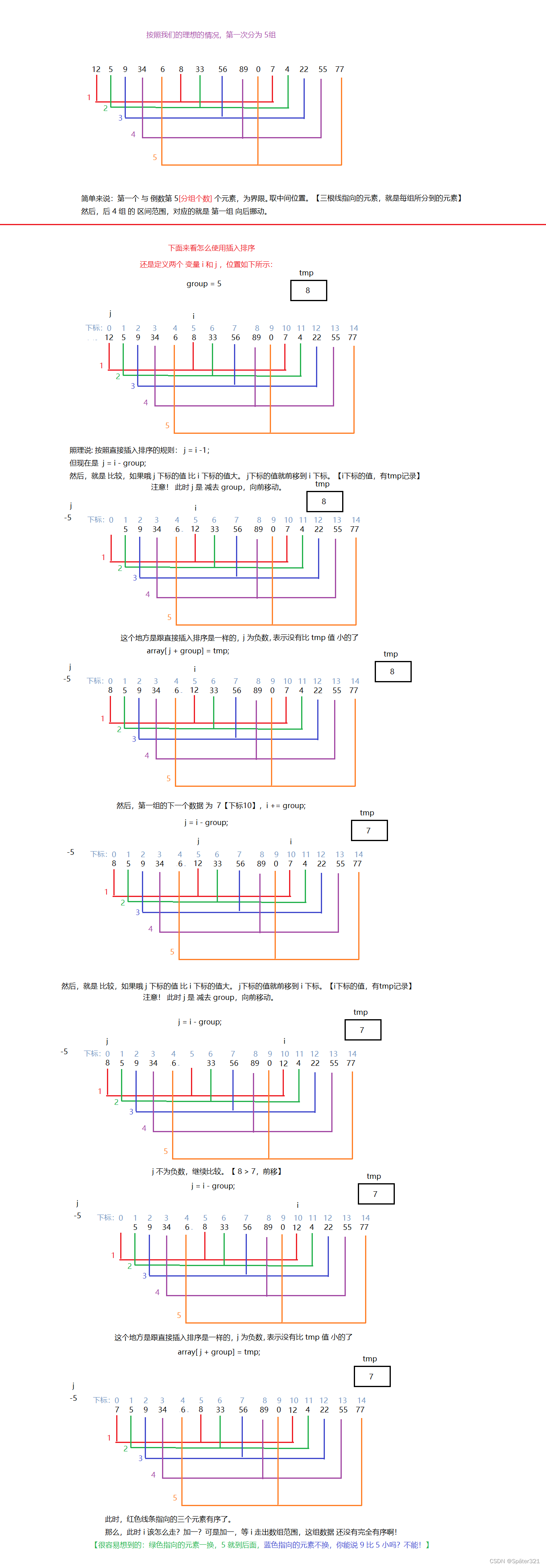
正常情况下我们进行分组的时候都是按照顺序进行分组的
比如说:
那么,问题来了!我们怎去确定分多少组,而且越分越少。
【取自清华大学出版的一本书《数据结构》】
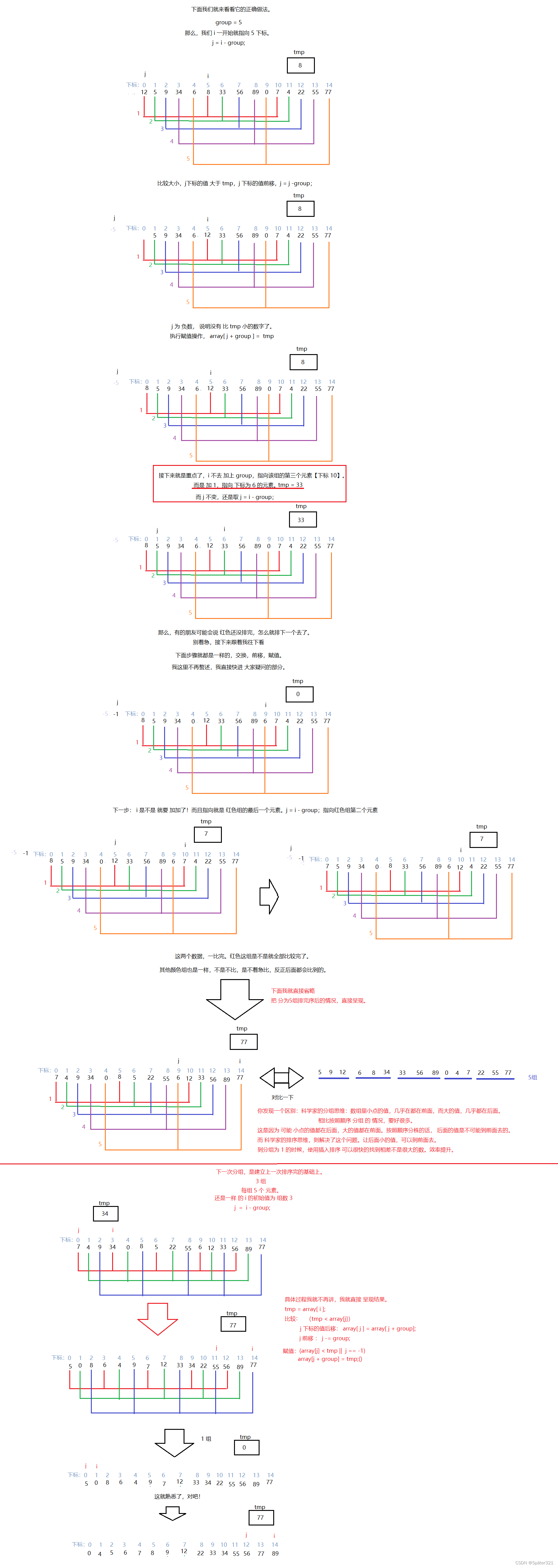
但是科学家的思维不同,他们分组的时候是跳着分组的
比如说:
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
4.2、模拟实现 - 希尔排序
/** 时间复杂度和增量有关系,所以无法得出准确的时间复杂度* 但只需要记住:在一定的范围里,希尔排序的时间复杂度为 O(N^1.3 ~ N^1.5)* 空间复杂度为 O(1)* 稳定性:不稳定* 判断稳定性的技巧:如果在比较的过程中 发生了 跳跃式交换。那么,就是不稳定的排序。* */public static void shell(int[] array,int group){for (int i = group; i < array.length; i++) {int j = i - group;int tmp = array[i];for( ; j >=0; j = j-group){if(tmp < array[j]){//交换元素array[j+group] = array[j];array[j] = tmp;}else {break;}}array[j+group] = tmp;}}public static void shellSort(int[] array){//将整个数组分为5组int gap = 5;while(gap > 1){//将分好组的数进行插入排序shell(array, gap);//循环得到分多少组,将分的组数按照 group / 2 来分组gap = gap / 2;}//循环结束,那就说明前面分好组的数都排序好了,只剩下最后的一组 就是 gap = 1的组shell(array, 1);}
五、选择排序
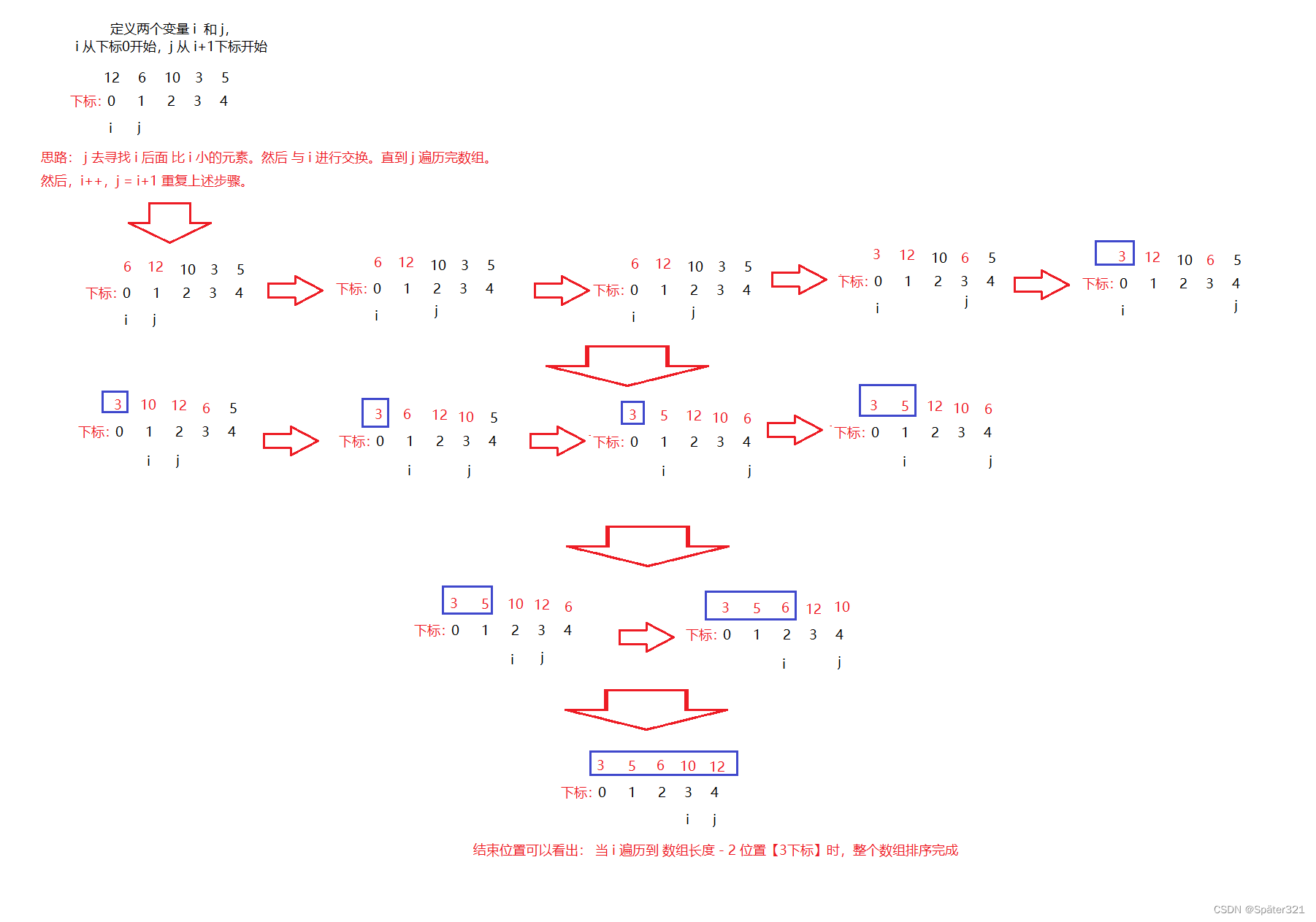
5.1、原理
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
优化
定义 一个 变量, 用来记录 此时的 i 后面最小值的下标。等 j 遍历完了,最小值的下标也就拿到了。此时,再进行交换。
这样就不必让上面那样,遇到比 i下标元素 小的,就交换。
5.2、模拟实现- 选择排序
/** 选择排序* 稳定性: 不稳定 见附图* 时间复杂度:O(N^2) 》》 外层循环 n -1,内层循环 n -1* 空间复杂度:O(1)* */public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {for (int j = i+1; j < array.length; j++) {if(array[i] > array[j]){int tmp = array[i];array[i] = array[j];array[j] = tmp;}}}}
5.3、双向选择排序 (了解)
每一次从无序区间选出最小 + 最大的元素,存放在无序区间的最前和最后,直到全部待排序的数据元素排完 。
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
public static void selectSortOP(int[] array){int low = 0;int high = array.length - 1;// [low,high] 表示整个无序区间while(low < high){int min = low;int max = low;for (int i = low+1; i <= high; i++) {if(array[i] < array[min]){min = i;}if(array[i] > array[max]){max = i;}}swap(array,min,low);if(max == low){max = min;}swap(array,max,high);low++;high--;}}public static void swap(int[] array,int x,int y){int tmp = array[x];array[x] = array[y];array[y] = tmp;}六、堆排序
前面一篇文章讲过:Java -数据结构,【优先级队列 / 堆】
/*** 堆排序* @param array*/public static void heapSort(int[] array){/** 时间复杂度:O(N * log2 N)* 空间复杂度:O(1)* 稳定性:不稳定* */int end = array.length - 1;while(end>0){int tmp = array[end];array[end] = array[0];array[0] = tmp;shiftDown(array,0,end);end--;}}// 创建一个大根堆public static void creMaxHeap(int[] arr){for (int preant = (arr.length-1-1)/2; preant >= 0; preant--) {shiftDown(arr,preant, arr.length);}}/*** 向下调整* @param arr 数组* @param preant 父亲节点的下标* @param len 调整结束位置*/public static void shiftDown(int[] arr, int preant, int len){int child = 2*preant+1;//孩子节点的下标while (child < len){if(child + 1 < len && arr[child] < arr[child+1]){child = child+1;}if(arr[child] > arr[preant]){int tmp = arr[child];arr[child] = arr[preant];arr[child] = tmp;preant = child;child = 2*preant+1;}else {break;}}}
七、冒泡排序
/** 时间复杂度:O(N^2) 【无论是最好情况,还是最坏情况,时间复杂度都不变】* 空间复杂度:O(1)* 稳定性:稳定【未发生跳跃式交换】* */public static void bubbleSort(int[] array){// 比较的趟数 = 数组的长度 - 1 【 0 ~ 3 一共 4趟】for (int i = 0; i < array.length-1; i++) {// 比较完一趟后,可以比较的元素个数减一。【因为靠后的数据已经有序】// 内循环中,之所以要减一个 1,是因为防止 下面的if语句 发生 数组越界异常for(int j = 0;j< array.length-1-i;j++){if(array[j] > array[j+1]){int tmp = array[j];array[j] = array[j+1];array[j+1] = tmp;}}}}
八、快速排序 - 重点
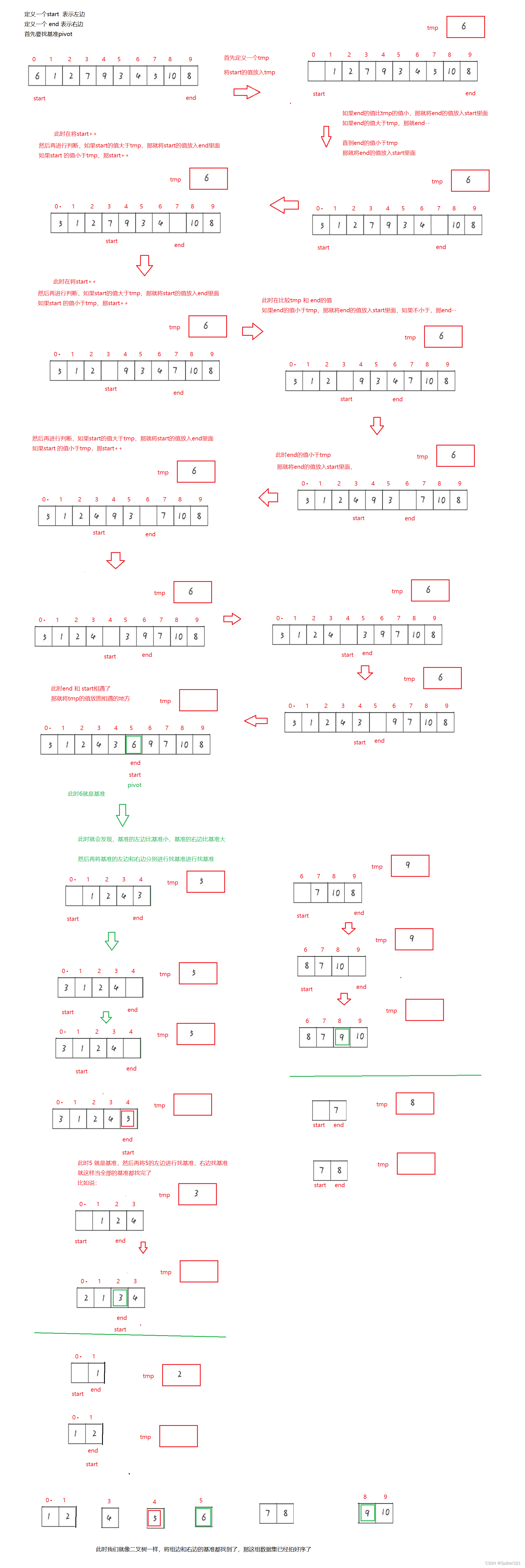
8.1、原理
- 从待排序区间选择一个数,作为基准值(pivot);
- Partition: 遍历整个待排序区间,将比基准值小的(可以包含相等的)放到基准值的左边,将比基准值大的(可以包含相等的)放到基准值的右边;
- 采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度 == 1,代表已经有序,或者小区间的长度 == 0,代表没有数据。
总结
快速排序,其实说白了 和 二叉树 很像,先根,再左,后右。利用递归去实现!
8.2、模拟实现 - 快速排序
/*** 快速排序 - 将这组数据从小到大排序* 时间复杂度:O(N^2) 【数据有序或者逆序的情况】* 最好情况【每次可以均匀的分割待排序序列】:O(N * log2 N)* 空间复杂度:O(N)[单分支的一棵树]* 最好:log2 N* 稳定性:不稳定* @param array*/public static void quickSort(int[] array){quick(array,0,array.length-1);}//排序public static void quick(int[] array, int left, int right){//排序if(left >= right){return;}//找基准int pivot = partition(array,left, right);quick(array,left,pivot-1);quick(array,pivot+1,right);}/*** 找基准*/public static int partition(int[] array, int start, int end){int tmp = array[start];while (start < end){while (start < end && array[end] >= tmp){end--;}array[start] = array[end];while (start < end && array[start] <= tmp){start++;}array[end] = array[start];}array[start] = tmp;return start;}
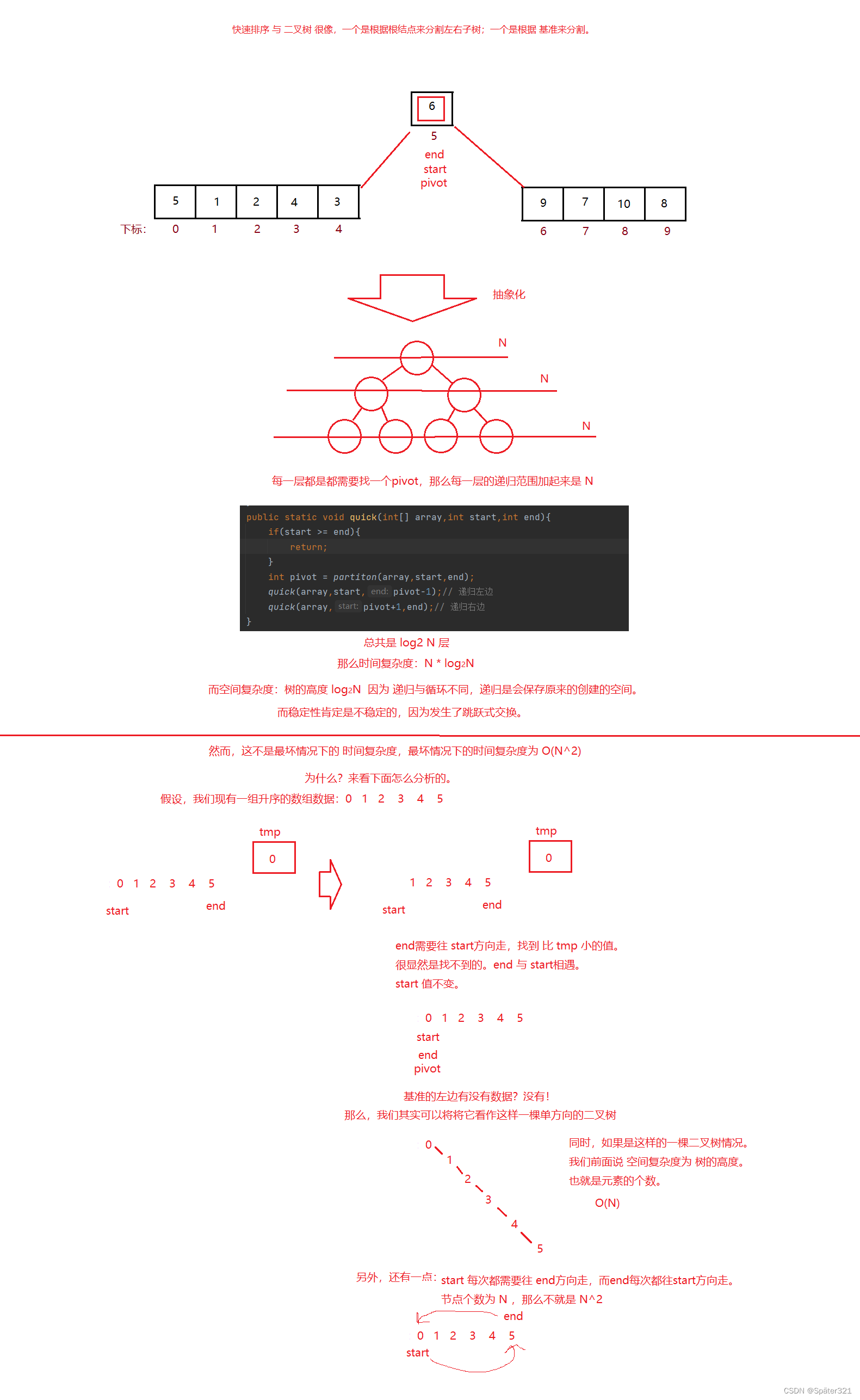
8.3、快速排序 的 时间 与 空间复杂度分析
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
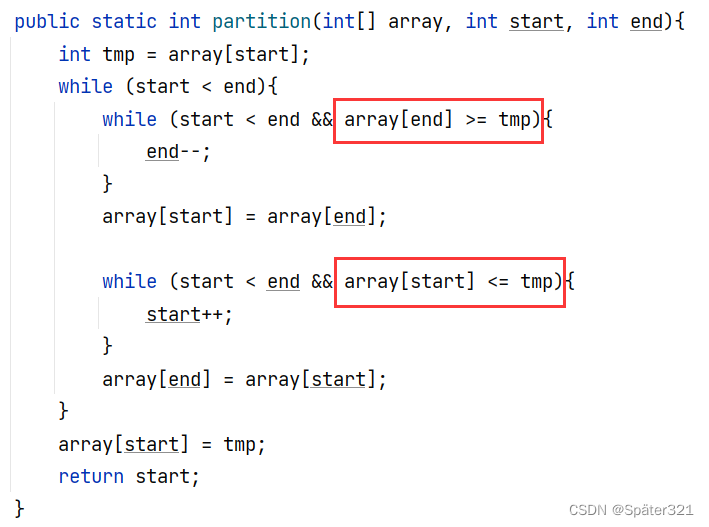
细节拓展
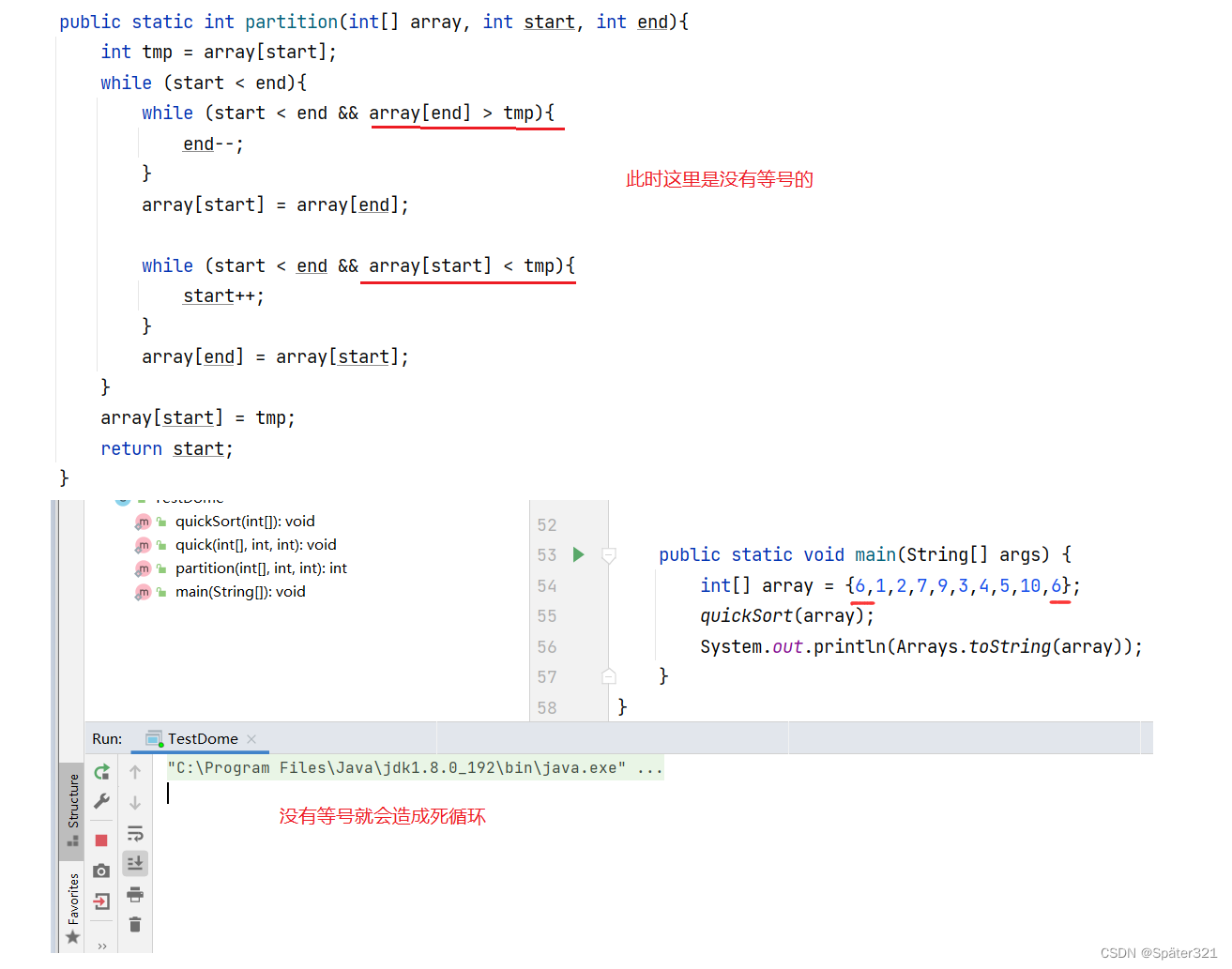
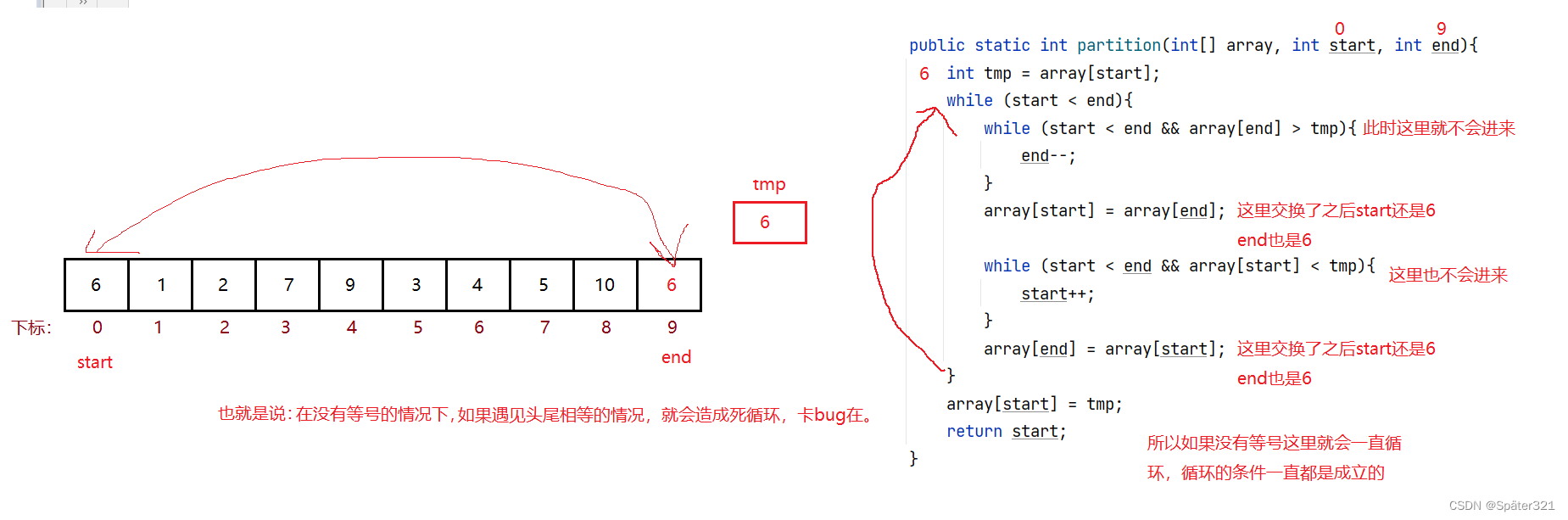
if语句中 比较大小的代码中 等号是不能省略的
当 下面框选的代码 没有等号时,会造成死循环。
我就改了一下,末尾元素的值。
那么,问题来了:为什么没有等号就死循环了?
所以,在 写快排的时候,比较大小的代码,记住一定要加上等号!!!!!
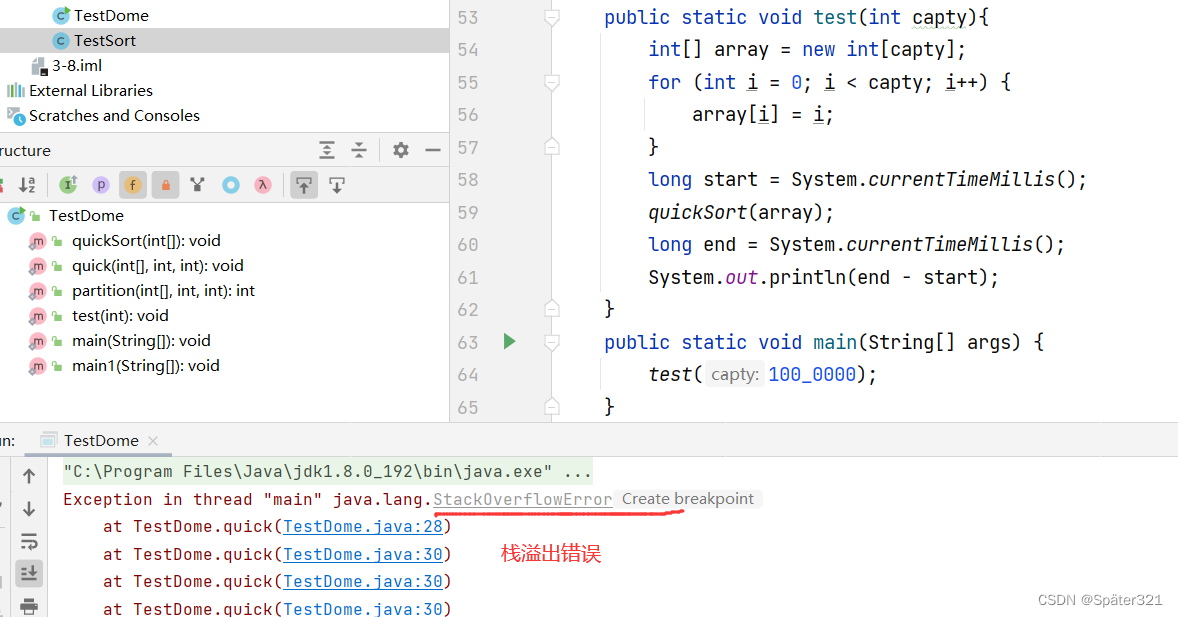
目前版本的 快排代码 不支持 大量数据进行排序 - 会导致栈溢出。
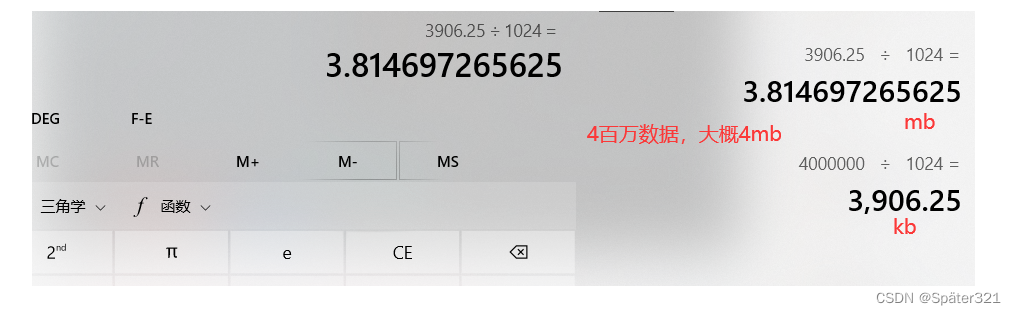
这是因为 我们递归的太深了,1百万数据,4百万字节。 1TB等于1024GB;1GB等于1024MB;1MB等于1024KB;1KB等于1024Byte(字节);1Byte等于8bit(位);
有的朋友会说:这才多大啊?栈怎么会被挤爆? 这是因为在递归的时候,开辟的栈帧【函数的信息,参数等等等…都有】,所以,每次开辟的栈帧不止 4byte。故栈被挤爆了。
所以,我们要优化快排的 代码。【优化:数据有序的情况】
基准值的选择 - 优化前的知识补充
1、选择边上(左或者右) 【重点,上面使用的就是这种方法】
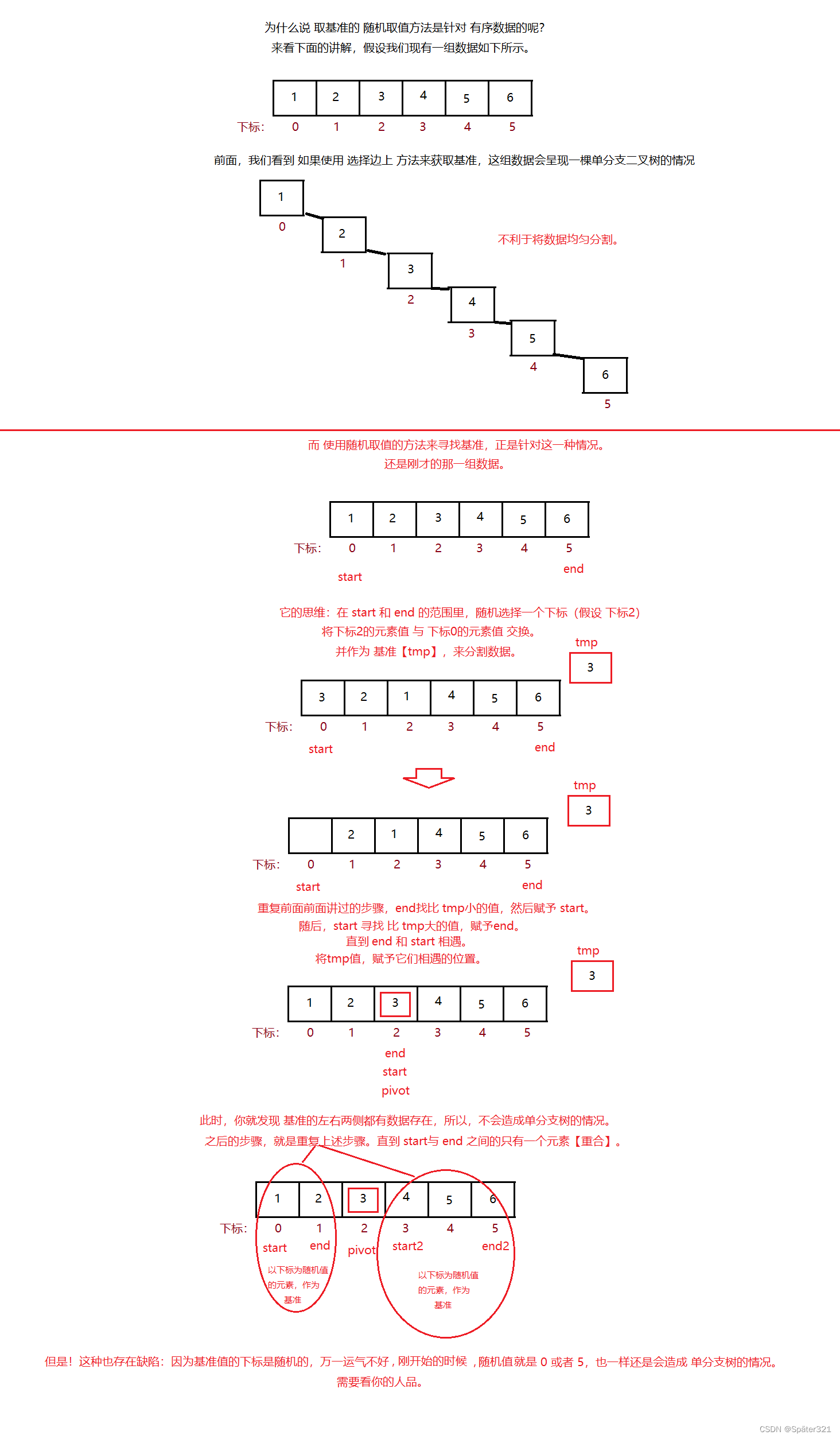
2、随机选择(针对 有序数据)【了解】
上图转载于:https://blog.csdn.net/DarkAndGrey/article/details/122792097
/** 时间复杂度:O(N^2) 【数据有序或者逆序的情况】* 最好情况【每次可以均匀的分割待排序序列】:O(N * log2 N)* 空间复杂度:O(N)[单分支情况]* 最好:log2 N* 稳定性:不稳定* */public static void quickSort(int[] array){quick(array,0, array.length-1);}public static void quick(int[] array,int start,int end){if(start >= end){return;}// 在找基准之前,先确定 start 和 end 的 中间值。[三数取中法]int midValIndex = findMidValIndex(array,start,end);//将它 与 start 交换。这样后面的程序,就不用改动了。swap(array,start,midValIndex);int pivot = partiton(array,start,end);quick(array,start,pivot-1);// 递归左边quick(array,pivot+1,end);// 递归右边}// 确定基准值下标private static int findMidValIndex(int[] array,int start,int end){// 确定 start 和 end 的中间下标int mid = start + ((end - start)>>>1);// == (start + end)/ 2// 确定 mid、start、end 三个下标,谁指向的元素是三个元素中的中间值if(array[end] > array[start]){if(array[start] > array[mid]){return start;}else if(array[mid] > array[end]){return end;}else{return mid;}}else{// array[start] >= array[end]if(array[end] > array[mid]){return end;}else if(array[mid] > array[start]){return start;}else {return mid;}}}// 交换两个下标元素private static void swap(int[] array,int x,int y){int tmp = array[x];array[x] = array[y];array[y] = tmp;}// 分割 - 找基准private static int partiton(int[] array,int start,int end){int tmp = array[start];while(start < end){while(start < end && array[end] >= tmp){end--;}// 此时 end 下标 元素的值 是 小于 tmp的。array[start] = array[end];while(start<end && array[start] <= tmp){start++;}array[end] = array[start];}array[start] = tmp;return start;}
8.4、快速排序 - 非递归实现
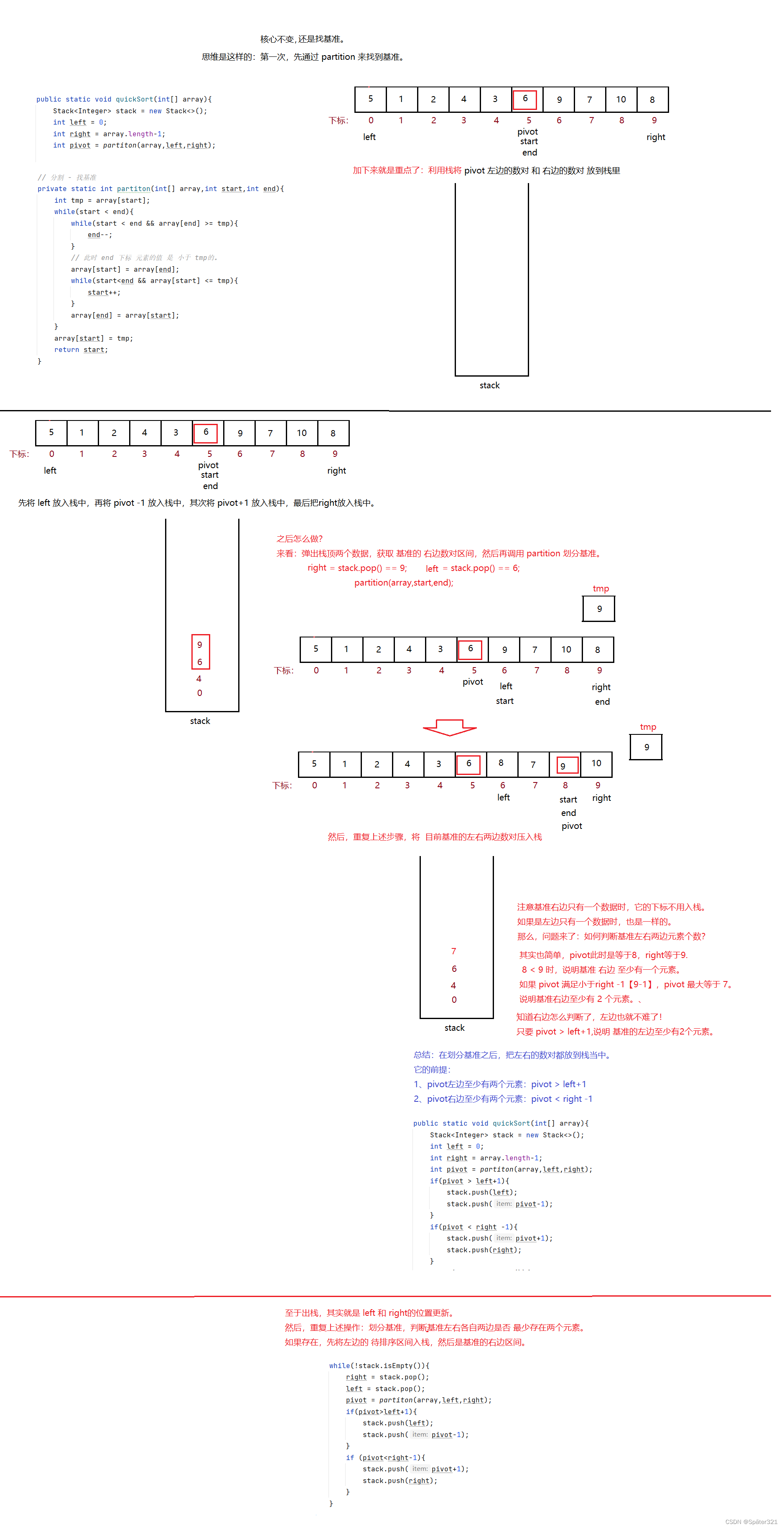
public static void quickSort(int[] array){Stack<Integer> stack = new Stack<>();int left = 0;int right = array.length-1;int pivot = partiton(array,left,right);if(pivot > left+1){stack.push(left);stack.push(pivot-1);}if(pivot < right -1){stack.push(pivot+1);stack.push(right);}while(!stack.isEmpty()){right = stack.pop();left = stack.pop();pivot = partiton(array,left,right);if(pivot>left+1){stack.push(left);stack.push(pivot-1);}if (pivot<right-1){stack.push(pivot+1);stack.push(right);}}}// 分割 - 找基准private static int partiton(int[] array,int start,int end){int tmp = array[start];while(start < end){while(start < end && array[end] >= tmp){end--;}// 此时 end 下标 元素的值 是 小于 tmp的。array[start] = array[end];while(start<end && array[start] <= tmp){start++;}array[end] = array[start];}array[start] = tmp;return start;}
九、归并排序 - 重点
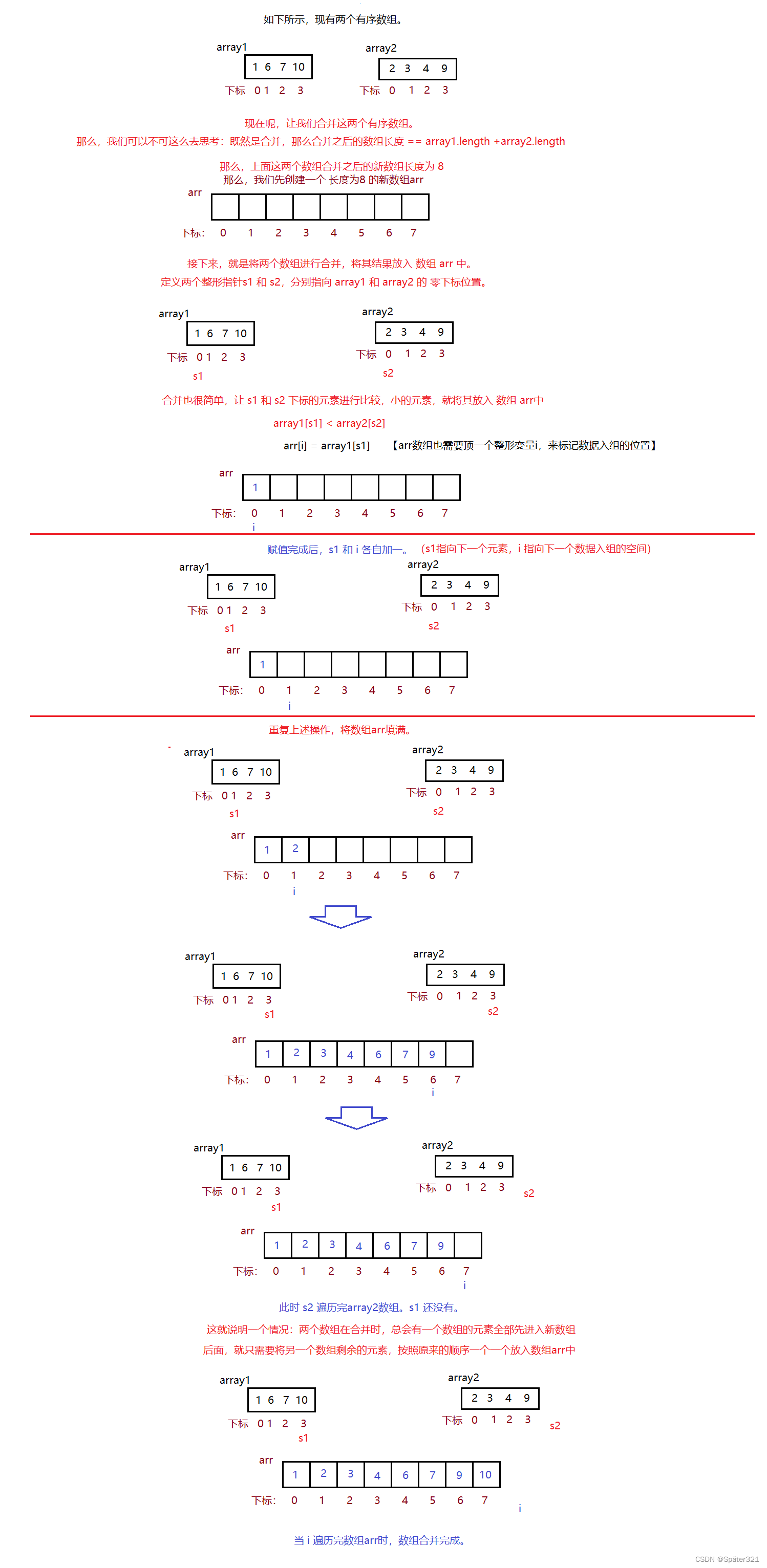
首先做一个题:将两个有序表合并成一个有序表,称为二路归并。【简单说就是 将两个有序数组合并为一个有序数组,称为二路合并】
//二路合并的代码如下public static int[] mergeArrays(int[] array1,int[] array2){if(array1 == null || array2 == null){return array1 == null ? array2: array1;}int[] arr = new int[array1.length + array2.length];int i = 0;// arr 的 遍历变量int s1 = 0;//array1 的 遍历变量int s2 = 0;//array2 的 遍历变量while(s1 < array1.length && s2 < array2.length){if(array1[s1] > array2[s2]){arr[i++] = array2[s2++];
// s2++;
// i++;}else{arr[i++] = array1[s1++];
// s1++;
// i++;}}// 循环结束,有一个数组的元素已经全部存入// 接下来就是将另一个数组的元素放入 arr 中while (s1 < array1.length){arr[i++] = array1[s1++];
// i++;
// s1++;}while (s2 < array2.length){arr[i++] = array2[s2++];
// i++;
// s2++;}return arr;}9.1、归并排序 - 原理
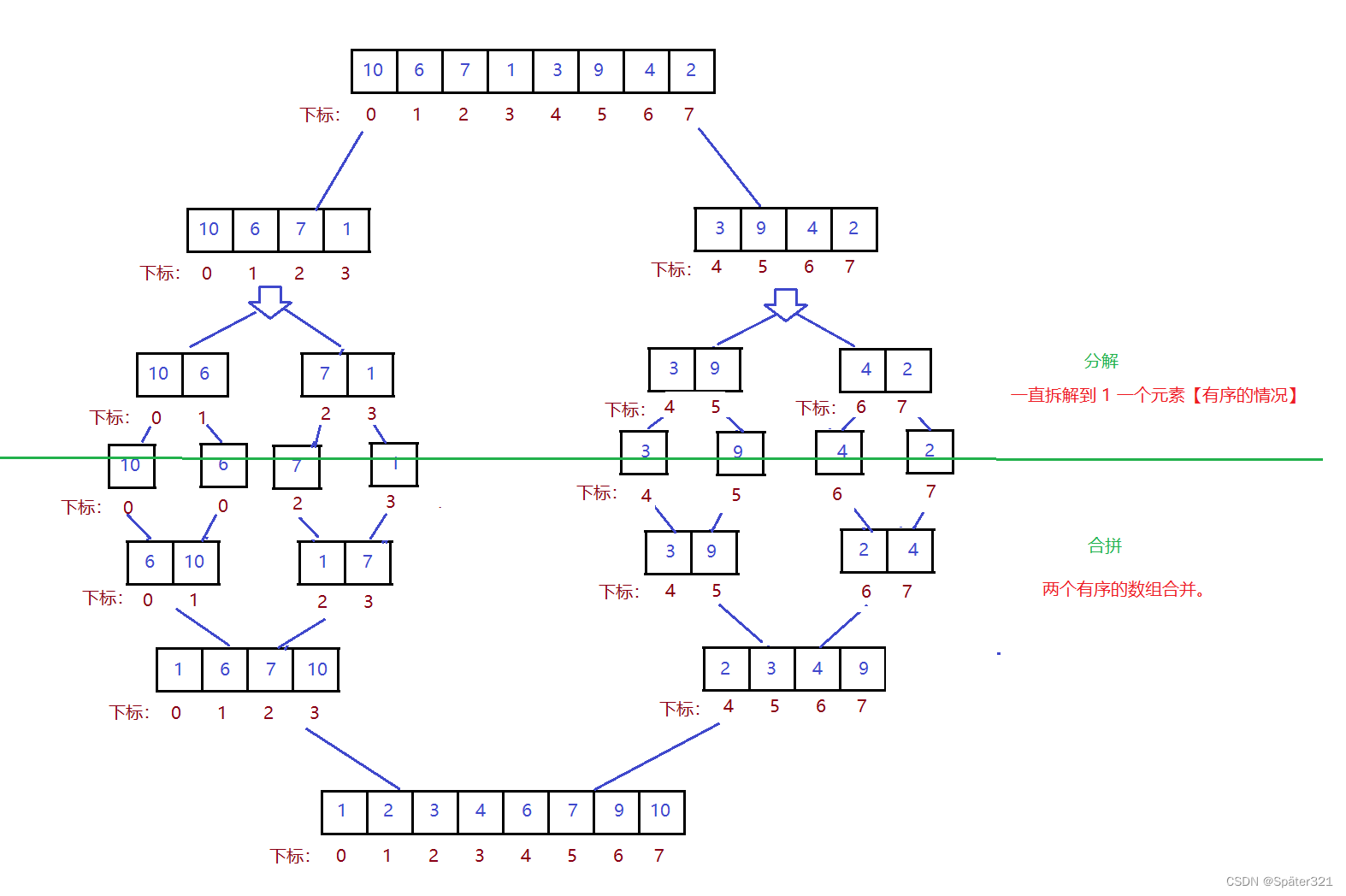
归并排序(MERGE - SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
难点1 - 如何将一个数组拆分成一个个单独数组【每个数组里只包含一个元素】。
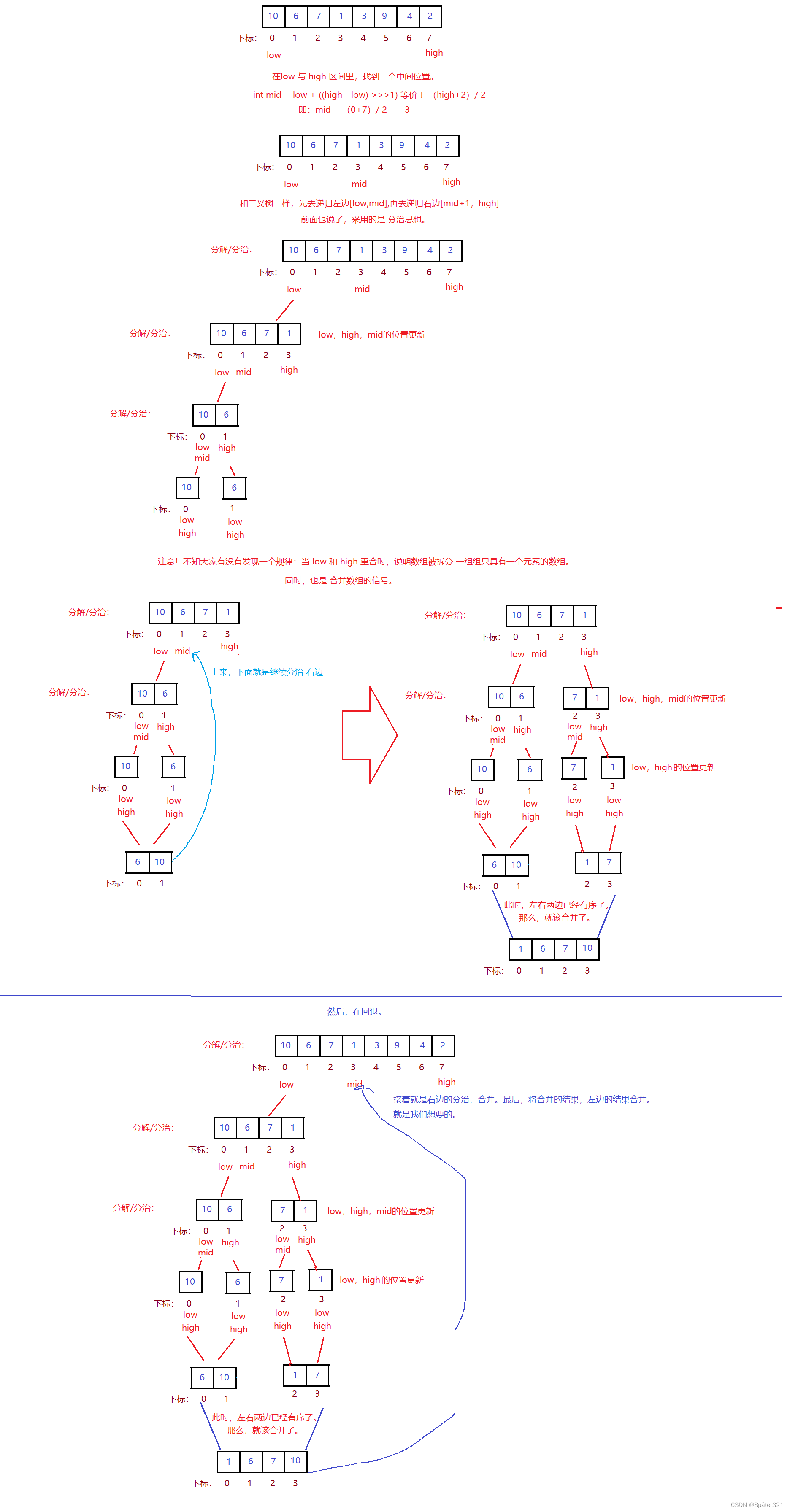
难点2 - 合并
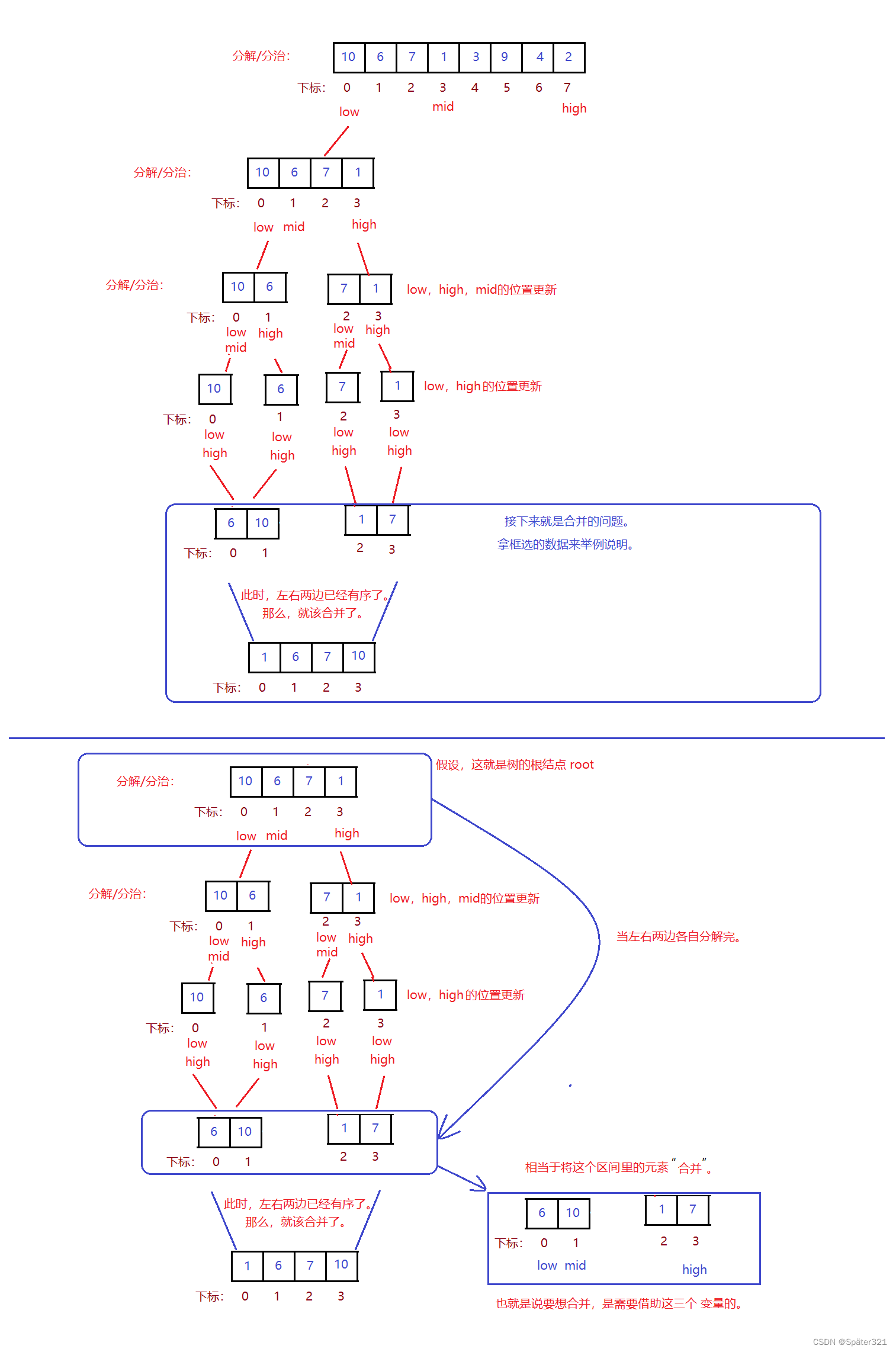
总程序
/** 时间复杂度:N * log2 N* 空间复杂丢:O(N)* 稳定性:稳定* */public static int[] mergeSort(int[] array){if(array == null){return array;}mergeSortFunc(array,0,array.length-1);return array;}private static void mergeSortFunc(int[] array,int low,int high){if(low >= high){return;}
// int mid = (high + low) >>> 1int mid = low + ((high - low) >>> 1);mergeSortFunc(array,low,mid);// 左边mergeSortFunc(array,mid+1,high);// 右边merge(array,low,mid,high);}private static void merge(int[] array,int low,int mid,int high){int[] arr = new int[high - low +1];int start1 = low;int end1 = mid;int start2 = mid+1;int end2 = high;int i = 0;while (start1 <= end1 && start2 <= end2){if(array[start1] > array[start2]){arr[i++] = array[start2++];}else{arr[i++] = array[start1++];}}while(start1 <= end1){arr[i++] = array[start1++];}while(start2 <= end2){arr[i++] = array[start2++];}for (int j = 0; j < arr.length; j++) {array[low++] = arr[j];}}
归并排序 - 时间与空间复杂度分析、稳定性

9.2、归并排序 - 非递归实现
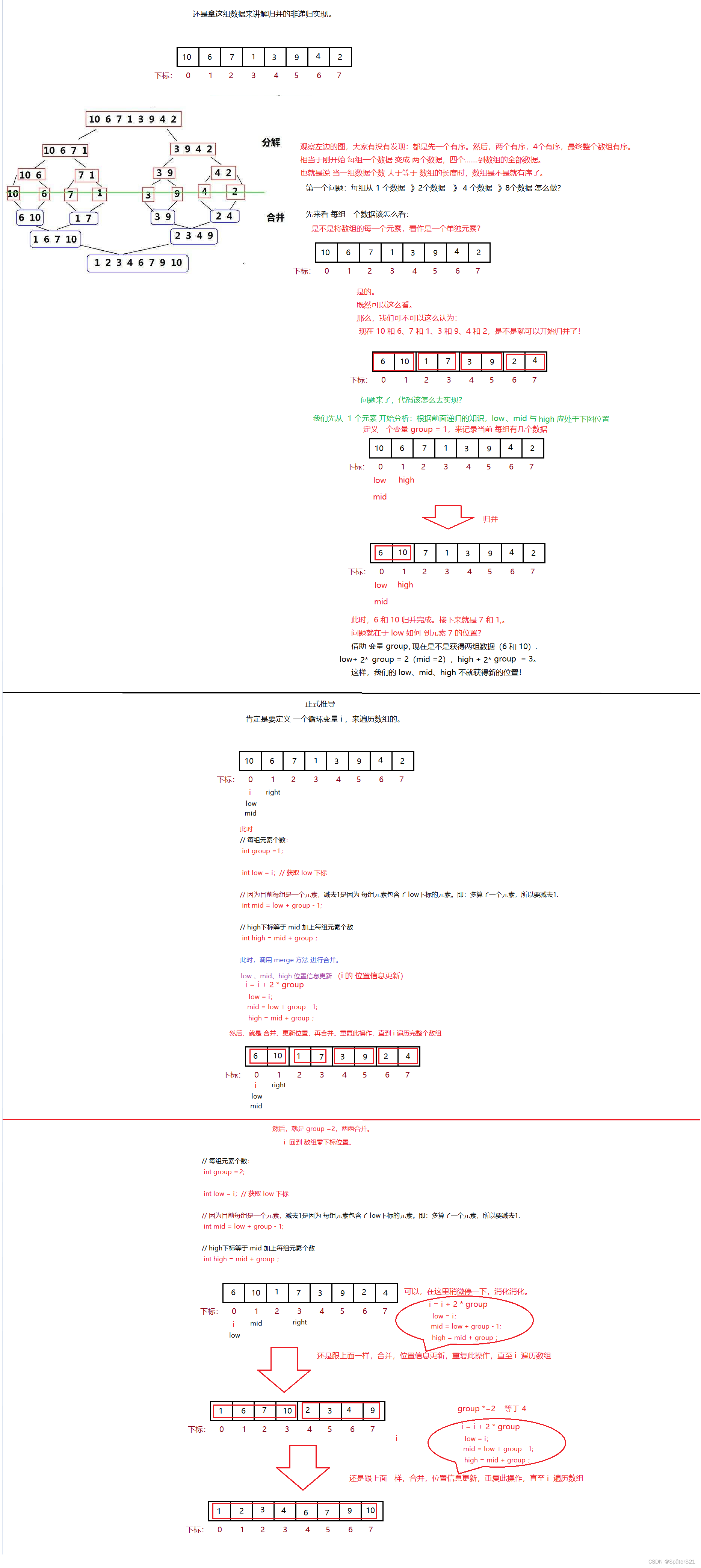
public static void mergeSort(int[] array){//归并排序非递归实现int groupNum = 1;// 每组的数据个数while(groupNum < array.length){// 无论数组含有几个元素, 数组每次都需要从下标 0位置,开始遍历。for(int i = 0;i<array.length;i+= groupNum * 2){int low = i;int mid = low + groupNum -1;// 防止越界【每组的元素个数,超过了数组的长度】if(mid >= array.length){mid = array.length-1;}int high = mid + groupNum;// 防止越界【超过了数组的长度】if(high >= array.length){high = array.length-1;}merge(array,low,mid,high);}groupNum *= 2;//每组的元素个数扩大到原先的两倍。}}public static void merge(int[] array,int low,int mid,int high){// high 与 mid 相遇,说明 此时数组分组只有一组,也就说没有另一组的数组与其合并// 即数组已经有序了,程序不用再往下走。if(high == mid){return;}int[] arr = new int[high -low + 1];int start1 = low;int end1 = mid;int start2 = mid+1;int end2 = high;int i = 0;while(start1 <= end1 && start2 <= end2){if(array[start1]>array[start2]){arr[i++] = array[start2++];}else{arr[i++] = array[start1++];}}while (start1 <= end1){arr[i++] = array[start1++];}while(start2 <= end2){arr[i++] = array[start2++];}for (int j = 0; j < arr.length; j++) {array[low++] = arr[j];}}
海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 200 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
十、排序总结
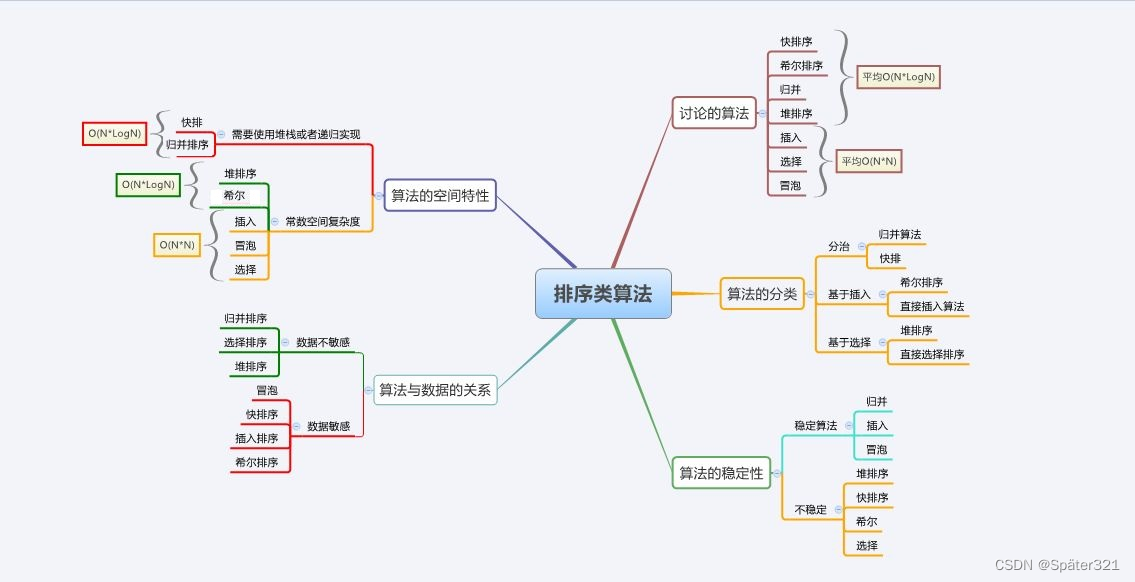
相关文章:

java - 数据结构,算法,排序
一、概念 1.1、排序 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 平时的上下文中,如果提到排序,通常指的是排升序(非降序)。 通常意义上的排序&#…...

二叉树经典14题——初学二叉树必会的简单题
此篇皆为leetcode、牛客中的简单题型和二叉树基础操作,无需做过多讲解,仅付最优解。有需要的小伙伴直接私信我~ 目录 1.二叉树的节点个数 2.二叉树叶子节点个数 3.二叉树第K层节点个数 4.查找值为X的节点 5.leetcode——二叉树的最大深度 6.leetc…...

基于NMOSFET的电平转换电路设计
一、概述: 在单片机系统中,5V、3.3V是芯片常用的电平。而在传输协议中(如IIC、SPI等协议),存在芯片与芯片的高电平和低电平定义的范围不一样,所以需要存在一个电平转换电路,来使芯片与芯片之间顺利的传输。 二、前置…...

mongoDB搭建集群
(学习自黑马)下载对应linux版本MongoDB源码下载地址:https://www.mongodb.com/download-center#community目前在一台服务器开三个端口模拟三个mongodb, 配置一个主节点27017,一个从节点27018,一个仲裁者27019配置主节点,副节点,仲裁节点(下面的创建文件一共有三份,通…...
[深入理解SSD系列 闪存2.1.5] NAND FLASH基本读操作及原理_NAND FLASH Read Operation源码实现
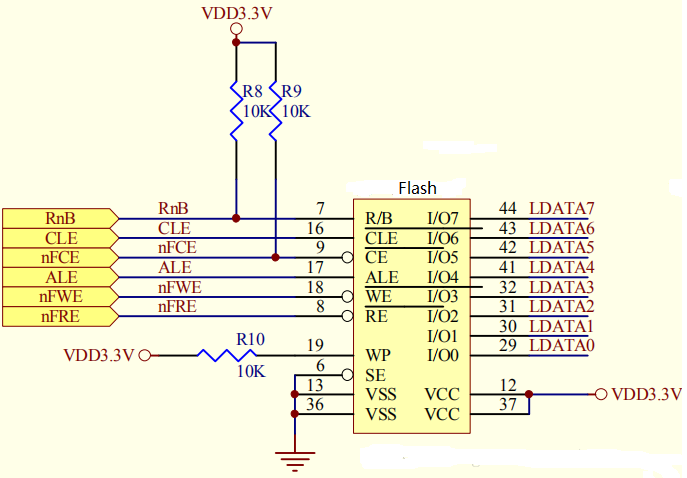
前言 上面是我使用的NAND FLASH的硬件原理图,面对这些引脚,很难明白他们是什么含义, 下面先来个热身: 问1. 原理图上NAND FLASH只有数据线,怎么传输地址? 答1.在DATA0~DATA7上既传输数据,又传输地址 当ALE为高电平时传输的是地址, 问2. 从NAND FLASH芯片手册可知,要…...

最新 JVM 面试经典问题
文章目录 说说JVM的内存布局?知道new一个对象的过程吗?知道双亲委派模型吗?说说有哪些垃圾回收算法?标记-清除复制算法标记-整理那么什么是GC ROOT?有哪些GC ROOT?垃圾回收器了解吗?年轻代和老年代都有哪些垃圾回收器?G1的原理了解吗?什么时候会触发YGC和FGC?对象什么…...
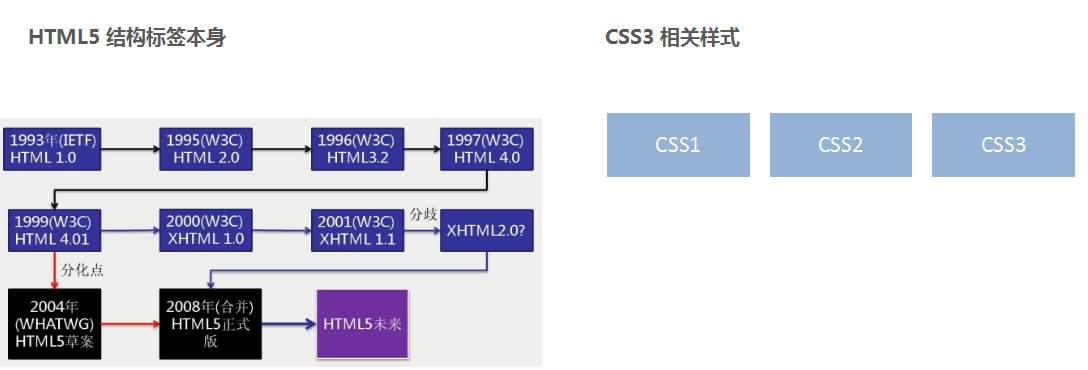
HTML5 和 CSS3 的新特性
目标能够说出 3~5 个 HTML5 新增布局和表单标签能够说出 CSS3 的新增特性有哪些HTML5新特性概述HTML5 的新增特性主要是针对于以前的不足,增加了一些新的标签、新的表单和新的表单属性等。 这些新特性都有兼容性问题,基本是 IE9 以上版本的浏览器才支持&…...

Vulnhub系列:FristLeaks
一、配置靶机环境以往的靶机,本人是在virtual box中,去配置,和vm上的kali进行联动,但是这个靶机需要DHCP,以往的方式可能不太行了,或者可以在virtual box中桥接成统一网卡。下面介绍下本人最有用的方法&…...

XWiki Annotation Displayer 存在任意代码执行漏洞(CVE-2023-26475)
漏洞描述 XWiki 是一个开源的企业级 Wiki 平台,Annotation Displayer 是 XWiki 中的一个插件,用于在 XWiki 页面上显示注释和其他相关内容。 该项目受影响版本存在任意代码执行漏洞,由于Annotation Displayer 对 Groovy 宏的使用没有限制&a…...

数字孪生GIS智慧风场Web3D可视化运维系统
随着国家双碳目标的实施,新能源发电方式逐渐代替了污染大气层的火力发电,其中风力发电相比于光伏发电具有能量密度高、发电小时数长、生命周期达20-25年之久等独特的优势。风能取之不尽、用之不竭,在新型能源互联网下,风力发电有可…...
- 网络请求和响应处理)
Retrofit核心源码分析(二)- 网络请求和响应处理
在上一篇文章中,我们详细分析了 Retrofit 中的注解解析和动态代理实现,本篇文章将继续深入研究 Retrofit 的核心源码,重点分析 Retrofit 如何进行网络请求和响应处理。 网络请求 在使用 Retrofit 发起网络请求时,我们可以通过定…...

STM32启动模式讲解与ICP下载电路
一、官方提供的启动模式说明硬件BOOT引脚接法表格从表格可以看出有三种启动模式,然后对应这不同的存储器启动,那我们现在疑问为啥有三种不能只有一种就好,还有存储器启动区域怎么区分,有些乱,带着这些疑问,…...
5款小巧好用的电脑软件,让你的工作生活更加高效!
不得不说良心好软件让大家好评连连,爱不释手,不像某些软件自带广告弹窗。这期就由我给大家安利几款电脑中的得力助手,看看你都用过几个? 1.桌面管理神器——Coodesker Coodesker是一款免费小巧、无广告,功能简单的桌…...

python线程池
假设我们必须多线程任务创建大量线程。 由于线程太多,因此可能会有很多性能问题,这在计算上会是最昂贵的。 一个主要问题可能是吞吐量受限。 我们可以通过创建一个线程池来解决这个问题。 一个线程池可以被定义为一组预先实例化和空闲的线程,…...

深入浅出PaddlePaddle函数——paddle.ones_like
分类目录:《深入浅出PaddlePaddle函数》总目录 相关文章: 深入浅出PaddlePaddle函数——paddle.Tensor 深入浅出PaddlePaddle函数——paddle.ones 深入浅出PaddlePaddle函数——paddle.zeros 深入浅出PaddlePaddle函数——paddle.full 深入浅出Padd…...

计算机组成原理(海明码效验)(3)-软件设计(二十四)
计算机组成原理(2)-软件设计(二十三)https://blog.csdn.net/ke1ying/article/details/129394115 一、总线 分为 内部总线、系统总线、外部总线。 内部总线:指芯片级别的总线,连接各个芯片。 系统总线&a…...

Linux2.2网络驱动程序编写
一.Linux系统设备驱动程序概述1.1 Linux设备驱动程序分类1.2 编写驱动程序的一些基本概念二.Linux系统网络设备驱动程序2.1 网络驱动程序的结构2.2 网络驱动程序的基本方法2.3 网络驱动程序中用到的数据结构2.4 常用的系统支持三.编写Linux网络驱动程序中可能遇到的问题3.1 中断…...
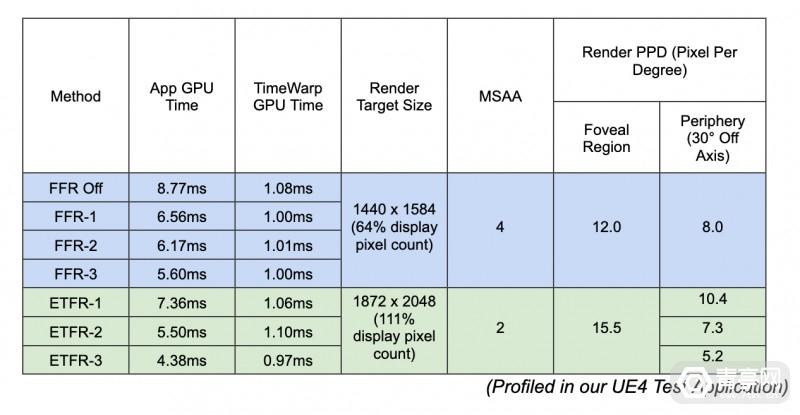
像素密度提升33%,Quest Pro动态注视点渲染原理详解
在Connect 2022上,Meta发布了Quest Pro,并首次在VR中引入动态注视点渲染(ETFR)功能,这是一种新型图形优化技术,特点是以用户注视点为中心,动态调节VR屏幕的清晰度(注视点中心最清晰、…...
【Linux实战篇】二、在Linux上部署各类软件
一、实战章节:在Linux上部署各类软件 二、MySQL数据库管理系统安装部署【简单】 简介 MySQL数据库管理系统(后续简称MySQL),是一款知名的数据库系统,其特点是:轻量、简单、功能丰富。 MySQL数据库可谓是…...

基于SpringBoot的学生会管理系统 源码
StudentUnionManagementSystem 基于SpringBoot的学生会管理系统 源码 链接 目录StudentUnionManagementSystem介绍软件架构使用说明1.页面登录2.首页3.成员信息管理4.角色信息管理5.权限管理6.活动管理7.文件管理8.活动展示介绍 学生会管理系统 SpringBoot Mybatis-plus shir…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...