z3-加法器实验
补码器加减法,运算方法简介
我们要知道什么是补码的加法,我们为什么要用补码的加法?
补码的加法其实就是将两个补码形式的二进制数字直接相加,处理的时候忽略超出固定位数的进位。补码的加法运算和无符号二进制数的加法操作一样,不需要额外处理负号或减法的逻辑
补码加法的具体操作步骤:
- 将两个补码数位对齐(确保位数一致)
- 诸位相加,处理进位
- 如果结果超出固定的位数,忽略超出部分的进位
例子:
假如我们在一个8位的系统中进行加法计算
- 5+3
- 5的补码:00000101
- 3的补码:00000011
- 00001000(结果位8)
- 5+(-3)
- 5的补码:00000101
- -3的补码:11111101
- 相加:10000010(结果位-2,最高位1表示结果是负数)
那么我们为什么要使用补码的加法?
补码的使用简化了计算机硬件的设计,使有符号的整数运算变得更加高效统一。补码的使用还简化了负数的表示和处理,使计算机更方便地进行各种数值运算。
在了解了补码的加法之后我们就可以尝试设计一位全加器电路了
构造一个一位全加器
首先要知道什么是全加器?
全加器是一种基本的数字电路,用于二进制数的加法运算。它能够同时处理两个二进制数的加法运算。它能够同时处理两个二进制位和一个来自低位的进位输入,并输出该位的和以及进位到高位的值。全加器是构建多位二进制加法器的基本模块。
全加器的功能
全加器有三个输入两个输出:
- 输入:两个被加的二进制位A和B,以及来自前一位的进位输入C_in_
- 输出:该位的和S和向更高位传递的进位输出C_out_
全加器的真值表
| A | B | C_in_ | S | C_out_ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
全加器的逻辑表达式
根据真值表,全加器的输入S和输出C可以用逻辑表达式表示:
- 和(sum)S:S = A XOR B XOR C_in_
- 进位(Carry)C_out_:C_out_ = (A * B) + (B * C_in_) + (A * C_in_)
一位全加器的电路实现
如下图所示:

功能封装
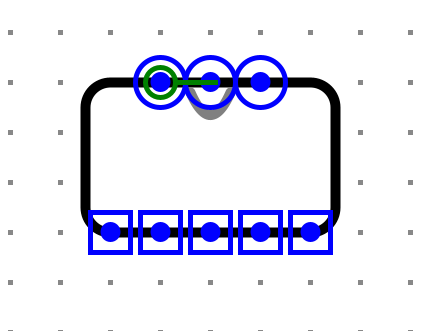
八位串行加法器
八位串行加法器是一种可以对两个8位二进制数进行加法运算的电路,串行加法器的工作原理是每次处理一个位,并将进位传递到下一位进行累加。以下是八位串行加法器的详细电路设计和验证。
电路设计
- 全加器:用于对两个二进制位及一个进位进行相加。
- 移位寄存器:用于存储和移位操作,分别存储两个8位数加数和结果
- **D触发器:**用于存储和传递进位
- 时钟:用于同步操作
电路示意图

使用具体数字验证
1. 初始化
- A寄存器:10101010
- B寄存器:01010101
- 进位 𝐶0:0
2. 逐位相加
- 第1次时钟脉冲:
- 取出最低位:A0 = 0, B0 = 1, 𝐶0=0
- 全加器计算:𝑆0=0⊕1⊕0=1
- 进位:𝐶1=(0⋅1)+(1⋅0)+(0⋅0)=0
- 移位:A -> 01010101, B -> 00101010
- 第2次时钟脉冲:
- 取出当前位:A1 = 1, B1 = 0, 𝐶1=0
- 全加器计算:𝑆1=1⊕0⊕0=1
- 进位:𝐶2=(1⋅0)+(0⋅0)+(1⋅0)=0
- 移位:A -> 00101010, B -> 00010101
- 第3次时钟脉冲:
- 取出当前位:A2 = 0, B2 = 1, 𝐶2=0
- 全加器计算:𝑆2=0⊕1⊕0=1
- 进位:𝐶3=(0⋅1)+(1⋅0)+(0⋅0)=0
- 移位:A -> 00010101, B -> 00001010
- 第4次时钟脉冲:
- 取出当前位:A3 = 1, B3 = 0, 𝐶3=0
- 全加器计算:𝑆3=1⊕0⊕0=1
- 进位:𝐶4=(1⋅0)+(0⋅0)+(1⋅0)=0
- 移位:A -> 00001010, B -> 00000101
- 第5次时钟脉冲:
- 取出当前位:A4 = 0, B4 = 1, 𝐶4=0
- 全加器计算:𝑆4=0⊕1⊕0=1
- 进位:𝐶5=(0⋅1)+(1⋅0)+(0⋅0)=0
- 移位:A -> 00000101, B -> 00000010
- 第6次时钟脉冲:
- 取出当前位:A5 = 1, B5 = 0, 𝐶5=0
- 全加器计算:𝑆5=1⊕0⊕0=1
- 进位:𝐶6=(1⋅0)+(0⋅0)+(1⋅0)=0
- 移位:A -> 00000010, B -> 00000001
- 第7次时钟脉冲:
- 取出当前位:A6 = 0, B6 = 1, 𝐶6=0
- 全加器计算:𝑆6=0⊕1⊕0=1
- 进位:𝐶7=(0⋅1)+(1⋅0)+(0⋅0)=0
- 移位:A -> 00000001, B -> 00000000
- 第8次时钟脉冲:
- 取出当前位:A7 = 1, B7 = 0, 𝐶7=0
- 全加器计算:𝑆7=1⊕0⊕0=1
- 进位:𝐶8=(1⋅0)+(0⋅0)+(1⋅0)=0
结果
最终输出结果的各位和为 𝑆7𝑆6𝑆5𝑆4𝑆3𝑆2𝑆1𝑆0=11111111,即十进制的255。进位输出 𝐶8=0,表示没有产生进位。
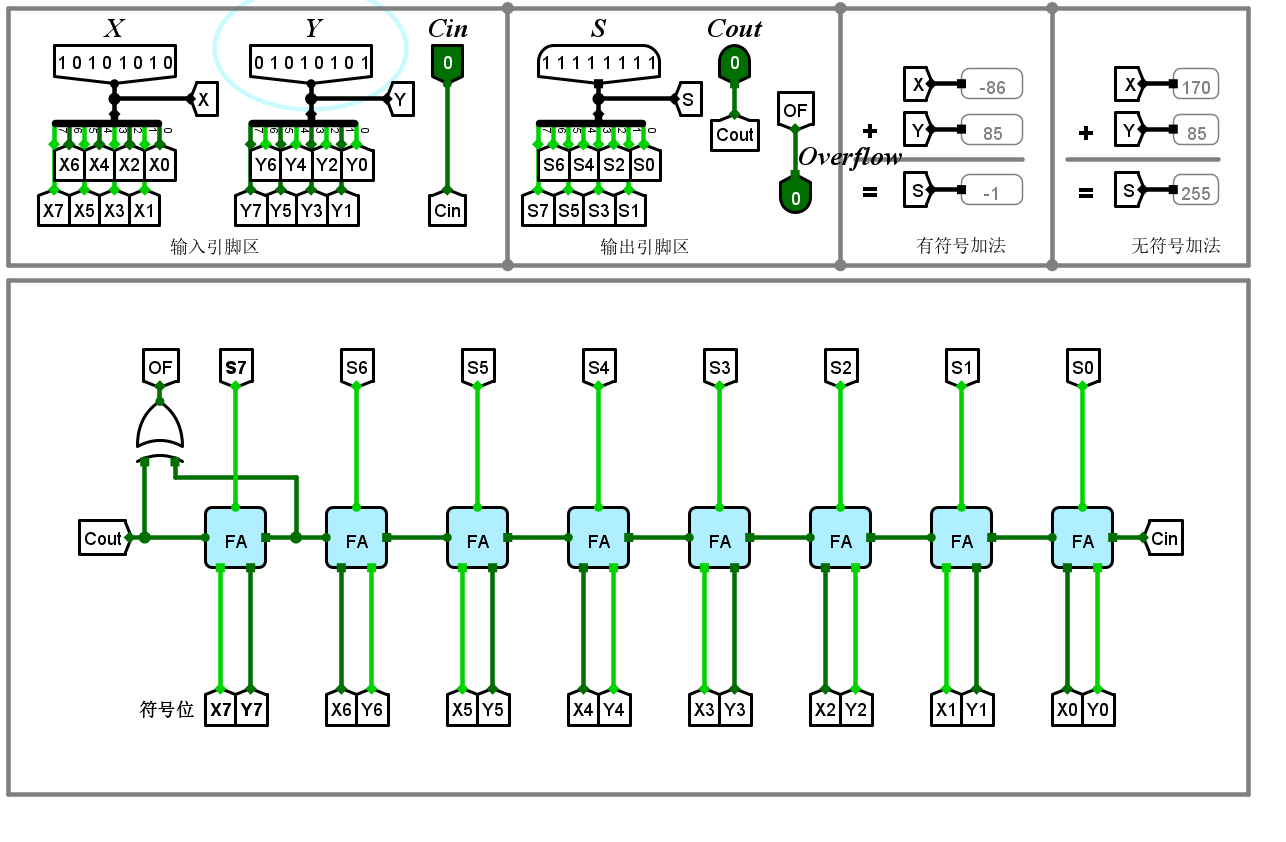
八位可控加减法器
8位可控加减法器是一种能够对两个8位二进制数进行加法或减法运算的电路。它通过控制信号来决定是执行加法还是减法。减法可以通过将被减数取补码并进行加法来实现。以下是详细的电路设计和使用具体数字进行验证的步骤。
电路设计
- 全加器:用于对两个二进制位及一个进位进行相加。
- 移位寄存器:用于存储和移位操作,分别存储两个八位数和结果。
- D触发器:用于存储和传递进位。
- 时钟:用于同步操作。
- 异或门:用于将减法操作转化为加法操作。
- 控制信号:用于选择加法或减法操作。
电路示意图
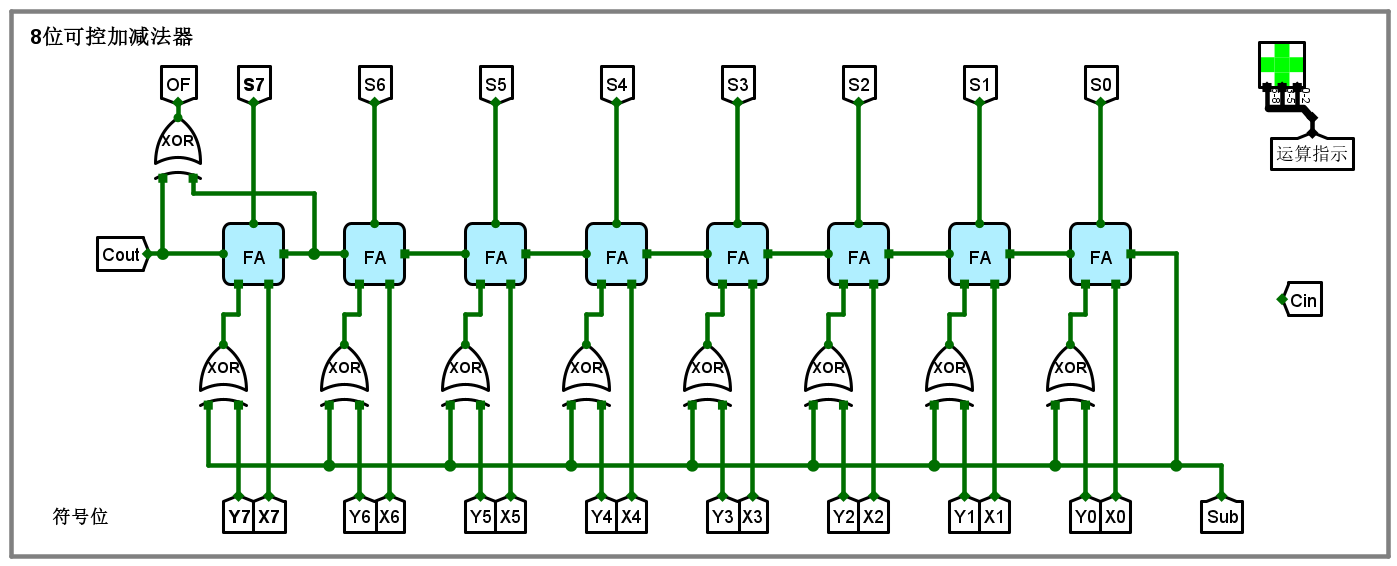
使用具体数字验证
加法验证
假设我们要相加的两个8位数是:
- A = 01101101 (十进制的109)
- B = 00111011 (十进制的59)
- 初始化:
- A寄存器:01101101
- B寄存器:00111011
- 进位 _C_0:0
- 控制信号 Add/Sub = 0(加法)
- 逐位相加
- 第1次时钟脉冲:
- 取出最低位:A0 = 1, B0 = 1, 𝐶0=0
- 全加器计算:𝑆0=1⊕1⊕0=0
- 进位:𝐶1=(1⋅1)+(1⋅0)+(0⋅0)=1
- 移位:A -> 00110110, B -> 00011101
- 第2次时钟脉冲:
- 取出当前位:A1 = 0, B1 = 1, 𝐶1=1
- 全加器计算:𝑆1=0⊕1⊕1=0
- 进位:𝐶2=(0⋅1)+(1⋅1)+(0⋅1)=1
- 移位:A -> 00011011, B -> 00001110
- 第3次时钟脉冲:
- 取出当前位:A2 = 1, B2 = 1, 𝐶2=1
- 全加器计算:𝑆2=1⊕1⊕1=1
- 进位:𝐶3=(1⋅1)+(1⋅1)+(1⋅1)=1
- 移位:A -> 00001101, B -> 00000111
- 第4次时钟脉冲:
- 取出当前位:A3 = 1, B3 = 0, 𝐶3=1
- 全加器计算:𝑆3=1⊕0⊕1=0
- 进位:𝐶4=(1⋅0)+(0⋅1)+(1⋅1)=1
- 移位:A -> 00000110, B -> 00000011
- 第5次时钟脉冲:
- 取出当前位:A4 = 0, B4 = 1, 𝐶4=1
- 全加器计算:𝑆4=0⊕1⊕1=0
- 进位:𝐶5=(0⋅1)+(1⋅1)+(0⋅1)=1
- 移位:A -> 00000011, B -> 00000001
- 第6次时钟脉冲:
- 取出当前位:A5 = 1, B5 = 1, 𝐶5=1
- 全加器计算:𝑆5=1⊕1⊕1=1
- 进位:𝐶6=(1⋅1)+(1⋅1)+(1⋅1)=1
- 移位:A -> 00000001, B -> 00000000
- 第7次时钟脉冲:
- 取出当前位:A6 = 0, B6 = 0, 𝐶6=1
- 全加器计算:𝑆6=0⊕0⊕1=1
- 进位:𝐶7=(0⋅0)+(0⋅1)+(0⋅1)=0
- 移位:A -> 00000000, B -> 00000000
- 第8次时钟脉冲:
- 取出当前位:A7 = 0, B7 = 0, 𝐶7=0
- 全加器计算:𝑆7=0⊕0⊕0=0
- 进位:𝐶8=(0⋅0)+(0⋅0)+(0⋅0)=0
结果
最终输出结果的各位和为 𝑆7𝑆6𝑆5𝑆4𝑆3𝑆2𝑆1𝑆0=10101000,即十进制的168。

减法验证
初始化
- A寄存器:01101101
- B寄存器:00111011
- 进位 _C_0:1(由于使用补码减法,初始进位为1)
- 控制信号 Add/Sub = 1(减法)
逐位计算(将B取反再加上A)
- 第1次时钟脉冲:
- 取出最低位:A0 = 1, B0 = 1
- 由于控制信号为1,B0取反:B0’ = 0
- 全加器计算:𝑆0=1⊕0⊕1=0
- 进位:𝐶1=(1⋅0)+(0⋅1)+(1⋅1)=1
- 移位:A -> 00110110, B -> 00011101
- 第2次时钟脉冲:
- 取出当前位:A1 = 0, B1 = 1
- 由于控制信号为1,B1取反:B1’ = 0
- 全加器计算:𝑆1=0⊕0⊕1=1
- 进位:𝐶2=(0⋅0)+(0⋅1)+(0⋅1)=0
- 移位:A -> 00011011, B -> 00001110
- 第3次时钟脉冲:
- 取出当前位:A2 = 1, B2 = 1
- 由于控制信号为1,B2取反:B2’ = 0
- 全加器计算:𝑆2=1⊕0⊕0=1
- 进位:𝐶3=(1⋅0)+(0⋅0)+(1⋅0)=0
- 移位:A -> 00001101, B -> 00000111
- 第4次时钟脉冲:
- 取出当前位:A3 = 1, B3 = 0
- 由于控制信号为1,B3取反:B3’ = 1
- 全加器计算:𝑆3=1⊕1⊕0=0
- 进位:𝐶4=(1⋅1)+(1⋅0)+(1⋅0)=1
- 移位:A -> 00000110, B -> 00000011
- 第5次时钟脉冲:
- 取出当前位:A4 = 0, B4 = 1
- 由于控制信号为1,B4取反:B4’ = 0
- 全加器计算:𝑆4=0⊕0⊕1=1
- 进位:𝐶5=(0⋅0)+(0⋅1)+(0⋅1)=0
- 移位:A -> 00000011, B -> 00000001
- 第6次时钟脉冲:
- 取出当前位:A5 = 1, B5 = 0
- 由于控制信号为1,B5取反:B5’ = 1
- 全加器计算:𝑆5=1⊕1⊕0=0
- 进位:𝐶6=(1⋅1)+(1⋅0)+(0⋅0)=1
- 移位:A -> 00000001, B -> 00000000
- 第7次时钟脉冲:
- 取出当前位:A6 = 0, B6 = 0
- 由于控制信号为1,B6取反:B6’ = 1
- 全加器计算:𝑆6=0⊕1⊕1=0
- 进位:𝐶7=(0⋅1)+(1⋅1)+(0⋅1)=0
- 移位:A -> 00000000, B -> 00000000
- 第8次时钟脉冲:
- 取出当前位:A7 = 0, B7 = 0
- 由于控制信号为1,B7取反:B7’ = 1
- 全加器计算:𝑆7=0⊕1⊕0=1
- 进位:𝐶8=(0⋅1)+(1⋅0)+(0⋅0)=0
结果
最终输出结果的各位和为 𝑆7𝑆6𝑆5𝑆4𝑆3𝑆2𝑆1𝑆0=00110010,即十进制的50。

相关文章:

z3-加法器实验
补码器加减法,运算方法简介 我们要知道什么是补码的加法,我们为什么要用补码的加法? 补码的加法其实就是将两个补码形式的二进制数字直接相加,处理的时候忽略超出固定位数的进位。补码的加法运算和无符号二进制数的加法操作一样&…...
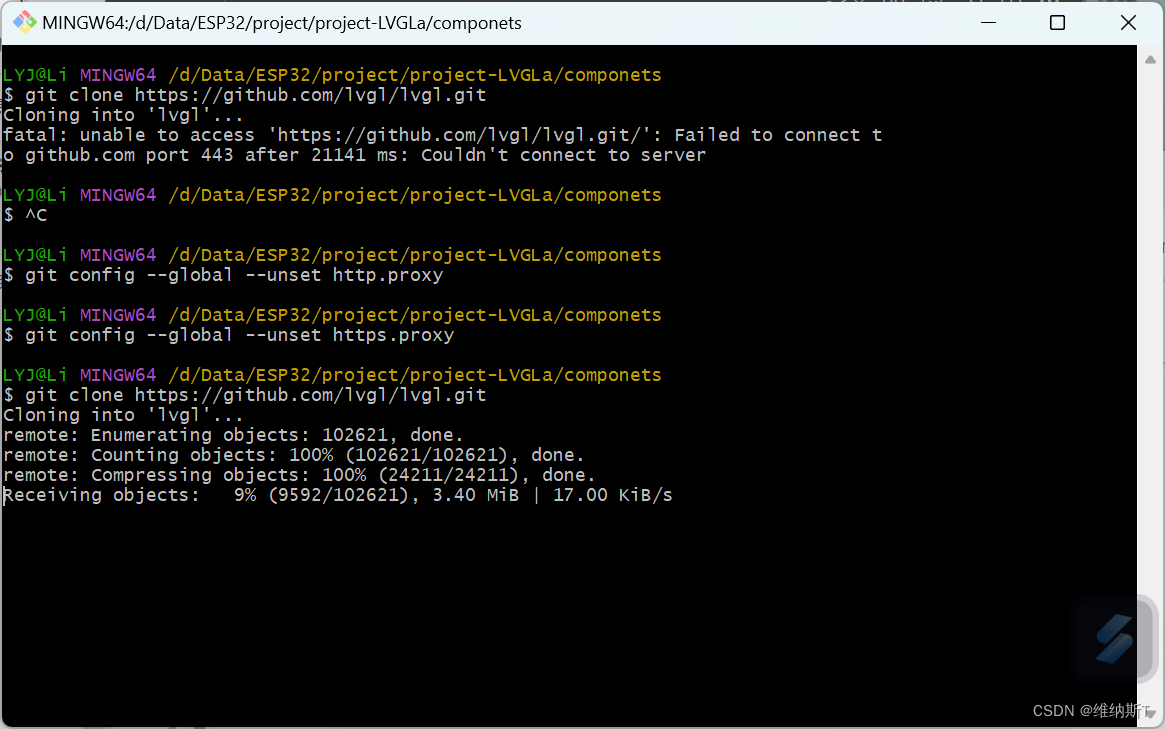
解决git克隆项目出现fatal无法访问git clone https://github.com/lvgl/lvgl.git
Windows 11系统 报错 $ git clone https://github.com/lvgl/lvgl.git Cloning into lvgl... fatal: unable to access https://github.com/lvgl/lvgl.git/: Failed to connect to github.com port 443 after 21141 ms: Couldnt connect to server 解决方法 git运行这两段代码…...

Vue中引入组件需要哪三步
在Vue中引入组件通常需要以下三步: 导入组件:首先,你需要在父组件中导入你想要使用的子组件。这通常是通过ES6的import语法完成的。 注册组件:接下来,你需要在父组件中注册这个子组件。这可以通过components选项完成&…...

到底该用英文括号还是中文括号?
这篇博客写的还挺详细的,不错。...

一个普通双非女生的秋招之路
大家好,我是小布丁。 先简单地做个自我介绍: 我今年本科毕业于某双非院校(属于那种没什么人听说过的小学校),学的是计算机专业,英语四级水平(没办法,六级确实没过)。我本…...

一个模型用了几层神经网络怎么算?
有权重参数的层算作一层,没有权重参数的就是参数不更新,不能称之为一层 有权重:卷积层、全连接层 没有权重的层:激活函数层、池化层 即数卷积层和全连接层的个数,就是这个模型用了几层神经网络。...

python获取cookie的方式
通过js获取cookie,避免反复登录操作。 经验证在JD上没有用,cookie应该无痕或者加密了,只能用单浏览器不关的模式来实现,但是代码留着,其他网站可能有用。 def cookie_set():driver webdriver.Chrome(optionschrome_…...
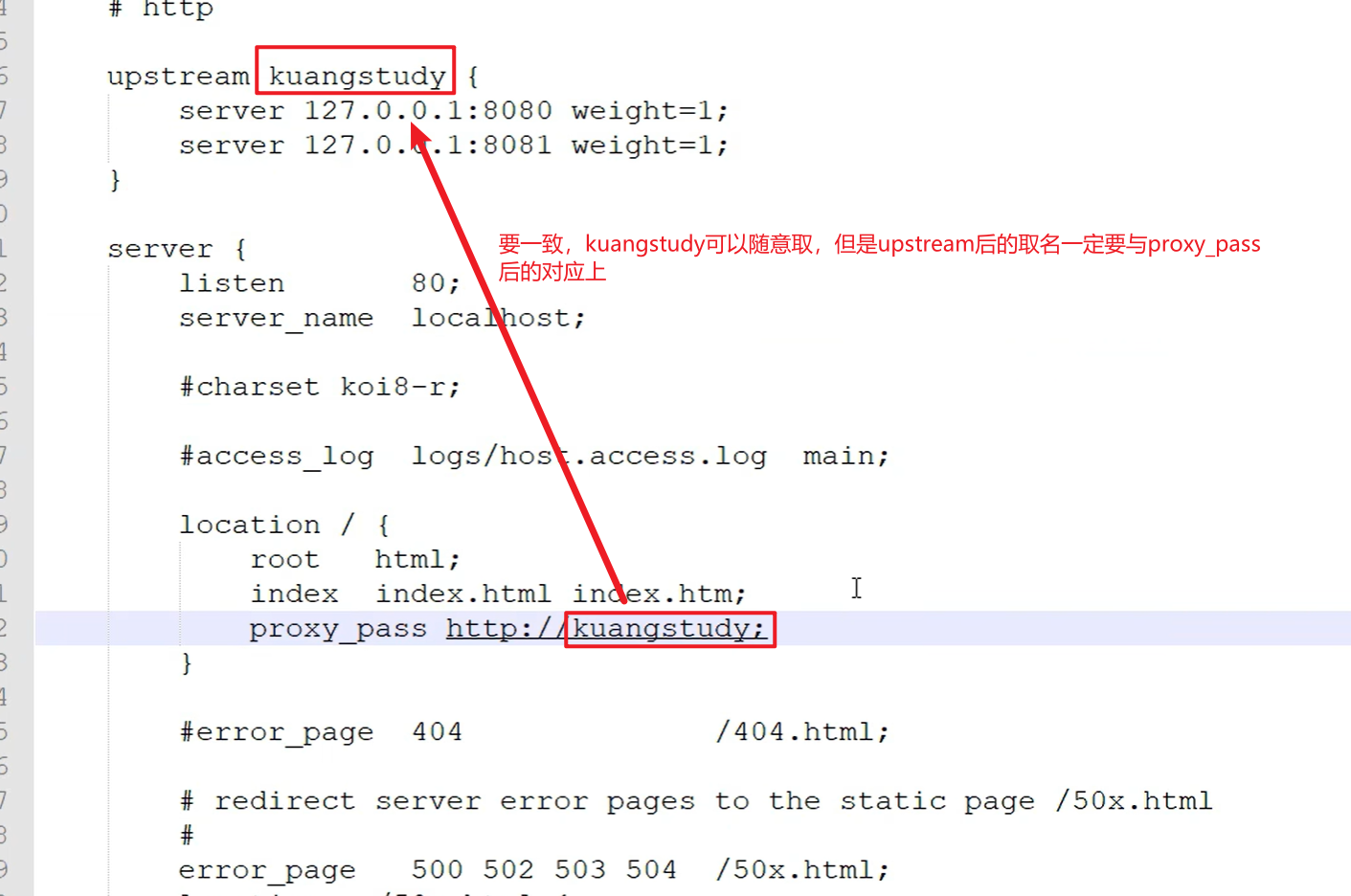
Nginx-狂神说
Nginx概述 公司产品出现瓶颈? 我们公司项目刚刚上线的时候,并发量小,用户使用的少,所以在低并发的情况下,一个jar包启动应用就够了,然后内部tomcat返回内容给用户。 但是慢慢的,使用我们平台…...
Python筑基之旅-运算符
目录 一、运算符 1、了解定义 2、理解意义 2-1、基本数据处理 2-2、条件判断 2-3、逻辑操作 2-4、赋值和更新 2-5、位操作 2-6、提高代码可读性 2-7、解决实际问题 2-8、学习其他编程语言的基础 3、探索方法 3-1、理解概念 3-2、练习基本运算 3-3、掌握优先级 …...
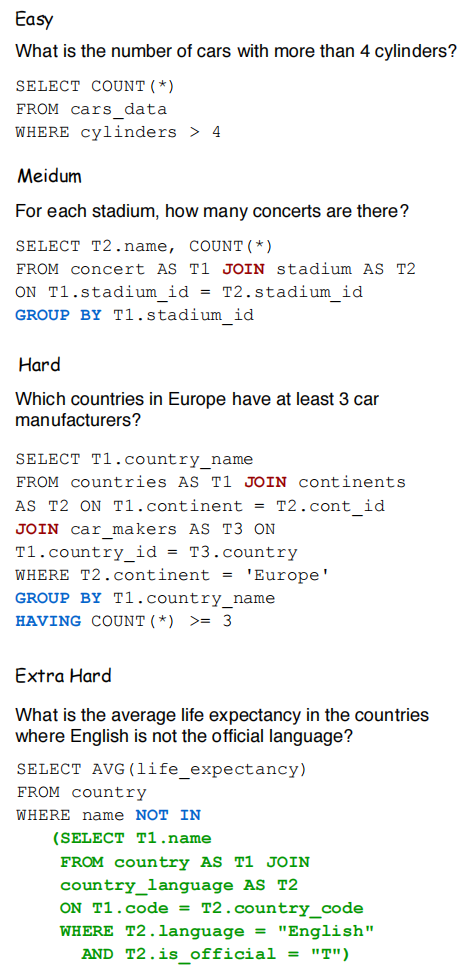
【Text2SQL】Spider 数据集
论文:Spider: A Large-Scale Human-Labeled Dataset for Complex and Cross-Domain Semantic Parsing and Text-to-SQL Task ⭐⭐⭐⭐⭐ EMNLP 2018, arXiv:1809.08887 Dataset: spider GitHub: github.com/taoyds/spider 一、论文速读 本文提出了 Text2SQL 方向的…...
语雀——云知识库/笔记
对于日常进行学习/创作或是记录学习、工作内容与心得的群体来说,能够及时同步的云笔记应用有着广泛的应用场景。近期,我也探索了许多款不同的软件应用,今天来分享一款很有特点的应用——语雀。 语雀,为每一个人提供优秀的文档和知…...

Java学习:电影查询简单系统
1.创建一个movice的对象来存放电影 里面设置构造器(有参和无参) package com.movie;public class movice {//创建一个movice的对象存放电影private int id;private String name;private double price;private double score;private String diector;pri…...

在Mac电脑下怎么部署QAnything?
在Mac电脑下部署QAnything,可以选择使用纯Python环境进行部署,这种方式不依赖GPU,适合在Mac等笔记本电脑上运行。以下是基于QAnything的纯Python环境安装教程的步骤[18]: 安装要求 Python 3.10(建议使用Anaconda3来管…...
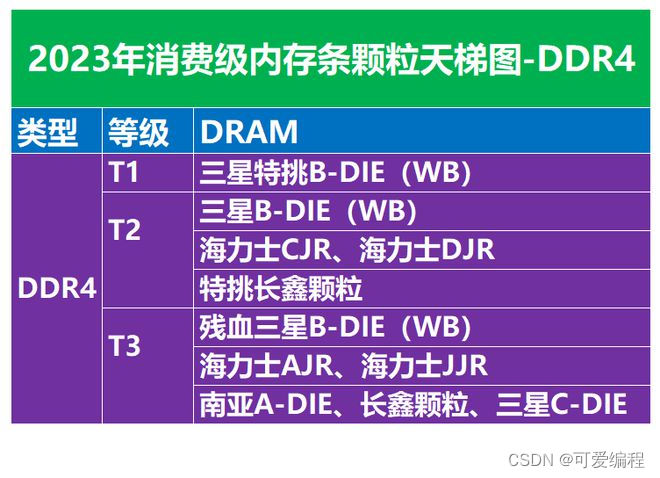
单条16g和双条8g哪个好
单条16g和双条8g各有优劣,具体选择要根据个人需求和电脑配置来决定。 以下是一些参考信息: •单条16g内存的价格比双条8g内存的价格低,而且16g的内存容量大,一条内存十分的方便。 •两条8g内存可以组成双通道,电脑运行速度要快一些。 •对于普通使用电脑的人群与热衷于…...

Microsoft VBA Excel 去重小工具
问题简述 在本工作表中,A1:B3单元格样式如下,通过名称管理器B列的单元格被命名为"LinkFile"、“SheetName”、“InputArea”,请实现以下功能:读取Excel文件中的数据,去除重复的数据,并记录每个数…...
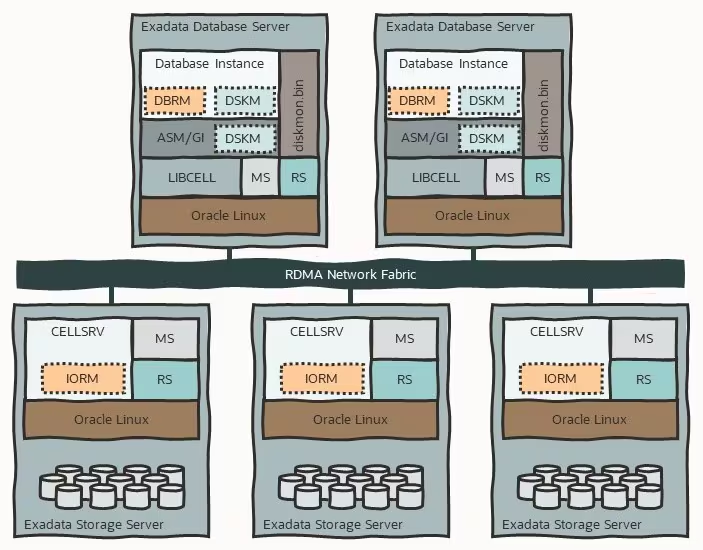
数据库管理-第194期 网络加速RDMA初探(20240526)
数据库管理194期 2024-05-26 数据库管理-第194期 网络加速RDMA初探(20240526)1 概念2 发展3 使用总结 数据库管理-第194期 网络加速RDMA初探(20240526) 作者:胖头鱼的鱼缸(尹海文) Oracle ACE A…...

C++小游戏 合集
生化危机 #include<conio.h> #include<string.h> #include<stdio.h> #include<stdlib.h> #include<windows.h> #include<time.h> #include<direct.h> int n,round,gold0; bool f1,f2,f3,deadfalse,PC_64Bit; char str[4]; struct n…...

【Python爬虫篇】Selenium在获取网页数据方面的使用及采集中国大学课程评论数据
1 selenium概述 1.什么是selenium? (1)Selenium是一个用于Web应用程序测试的工具。 (2)Selenium 测试直接运行在浏览器中,就像真正的用户在操作一样。 (3)支持通过各种driver&#…...
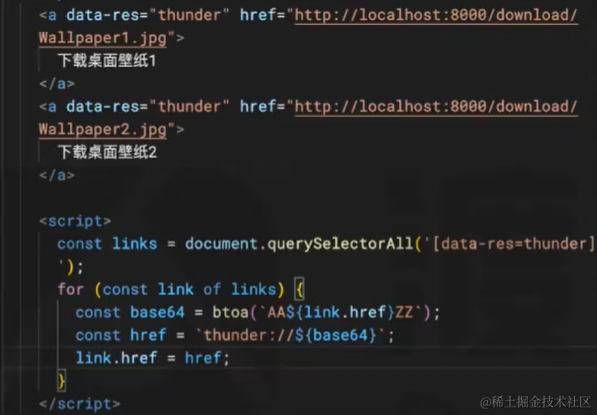
【JavaScript】文件下载
文件下载的消息格式 服务器只要在响应头中加入 Content-Disposition: attachment; filename"kxx" 即可触发浏览器的下载功能其中: attachment 表示附件,浏览器看到此字段,触发下载行为(不同的浏览器下载行为有所区别&…...

利用Python去除PDF水印
摘要 本文介绍了如何使用 Python 中的 PyMuPDF 和 OpenCV 库来从 PDF 文件中移除水印,并将每个页面保存为图像文件的方法。我们将深入探讨代码背后的工作原理,并提供一个简单的使用示例。 导言 简介:水印在许多 PDF 文件中都很常见&#x…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
