完全背包之零钱兑换I
上次分享完完全背包问题的解决思路后,这次分享一道和完全背包有关的leetcode题。
零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];for(int i = 1;i <= amount;i++){dp[i] = Integer.MAX_VALUE;}dp[0] = 0;for(int i = 0;i < coins.length;i++){for(int j = 0;j <= amount;j++){if(j >= coins[i] && dp[j - coins[i]] != Integer.MAX_VALUE){dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];}
}
这道题和完全背包问题相同点就是硬币的数量是无限的,可以重复使用,不同的是完全背包问题是使得背包里面物品的价值最大,不一定要装满背包,这道题则是恰好装满背包,要求使用的物品数量最少。解决思路也是装与不装,不装则是dp[j],装的话,背包容量就需要减去物品重量,此时加上的不再是物品的价值,而是物品的数量,仅装入一个物品,物品数加1,要求硬币数量最少,所以要取最小值。这里有一个需要强调的点,就是dp数组的初始化问题,对于这种要求恰好装满背包,求最值的问题,dp数组的初始化首元素一般都是0,其次其余元素就需要看要求的是最大值还是最小值,这里要求物品数量最少,所以其余元素初始化为整数最大值。在上一篇的完全背包问题时,遇到恰好装满背包,背包价值最大,这是dp首元素为0,其余元素则初始化为整数最小值。
这里以上述示例说明代码的执行流程。这里钱币的面值即是物品的体积,也是物品的价值,面值有1,2和5,总金额为11,所以dp数组初始化为11。dp数组如下所示,dp[j]的含义是金额为j需要的最小硬币数量为dp[j]:

之后遍历面值1,当背包容量j(总金额)为0时,不满足j >= coins[0],不进入if,背包容量j(总金额)为1时,j = coins[0],并且j - coins[0] = 0,可以装下,dp[1] = min(dp[j], dp[j - coins[i]] + 1) = dp[0] + 1 = 1。这里就很好的说明为什么dp[0]为什么要初始化为0,不初始化为0,对结果有影响,而且dp[1]要初始化为整数最大值,如果初始化为别的数,如0的话,这里得到的结果就不是1,而是0,所以其余dp元素要初始化为整数最大值。背包容量j(总金额)为2时,dp[2] = min(dp[2], dp[j - coins[i]] + 1) = dp[2 - coins[0]] + 1 = dp[1] + 1 = 1 + 1 = 2,dp[3] = dp[2] + 1 = 3,如此重复,遍历完面值1,dp数组如下:

之后遍历面值2,当背包容量j(总金额)为0和1时,不满足j >= coins[1],保持原值,当j等于2时,j = coins[1],dp[2] = min(dp[2],dp[j - coins[1]] + 1) = min(2, dp[0] + 1) = 1,用于dp是一维滚动数组,因此dp[2]的值是1,现在遍历面值2时,dp[2]为1,接着j = 3,dp[3] = min(3,dp[3 - 2] + 1) = dp[1] + 1 = 2,dp[4] = min(4, dp[4 - 2] + 1) = dp[2] + 1 = 1 + 1 = 2,此时的dp[2]为1,在j = 2时,修改了dp[2]的值。dp[5] = min(5, dp[5 - 2] + 1) = dp[3] + 1 = 3,dp[6] = 3,如此重复遍历,得到dp数组如下:

之后遍历面值5,当当背包容量j(总金额)为0,1,2,3,4时,不满足j >= coins[1],保持原值,j等于5,dp[5] = min(3, dp[5 - 5] + 1) = 1,dp[6] = min(3, dp[6 - 5] + 1) = 1 + 1 = 2,如此重复,得到dp数组如下,这里就不再展开说明,遍历完所有面值,返回dp[11]即为最终结果。

相关文章:

完全背包之零钱兑换I
上次分享完完全背包问题的解决思路后,这次分享一道和完全背包有关的leetcode题。 零钱兑换 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果…...

Flutter 中的 FittedBox 小部件:全面指南
Flutter 中的 FittedBox 小部件:全面指南 在Flutter的丰富布局小部件中,FittedBox扮演着一个独特而重要的角色。它是一个灵活的组件,用于将子组件的大小和位置适应到给定的约束条件中。本文将提供FittedBox的全面指南,帮助你了解…...
Java的线程的使用
一.两种创建线程的方式 1.继承Thread类(匿名内部类) 创建方式: 1.定义一个子类继承Thread,重写run方法 2.创建子类对象, 3.调用子类对象的start方法(启动还是执行的run方法) 优缺点&#x…...
)
行为型模式 (Python版)
模板方法模式 """案例:写简历内容:最近有个招聘会,可以带上简历去应聘了。但是,其中有一家公司不接受简历,而是给应聘者发了两张公司自己定制的简历表,分别是A类型的简历表和B类型的简历表…...
vscode:如何解决”检测到include错误,请更新includePath“
vscode:如何解决”检测到include错误,请更新includePath“ 前言解决办法1 获取includePath路径2 将includePath路径添加到指定文件3 保存 前言 配置vscode是出现如下错误: 解决办法 1 获取includePath路径 通过cmd打开终端,输入如下指令&a…...

区块链会议投稿资讯CCF A--USENIX Security 2025 截止9.4、1.22 附录用率
会议名称:34th USENIX Security Symposium CCF等级:CCF A类学术会议 类别:网络与信息安全 录用率:2023年接收率29%,2024录用的区块链相关文章请查看 Symposium Topics System security Operating systems security …...

vue实现可拖拽移动悬浮球
封装悬浮球组件,文件名s-icons.vue <template><div ref"icons" class"icons-container" :style"{ left: left px, top: top px }"><slot></slot></div> </template> <script> export …...

立体库堆垛机的精密构造与功能(收藏版)
导语 大家好,我是社长,老K。专注分享智能制造和智能仓储物流等内容。 新书《智能物流系统构成与技术实践》 在现代物流仓储体系中,堆垛机以其高效、精准的操作能力,成为了自动化存储与检索系统的关键所在。 其复杂的构造和多样化的…...

算法提高之你能回答这些问题吗
算法提高之你能回答这些问题吗 核心思想:线段树 用sum,lmax,rmax,tmax分别存线段长度,最大前缀,最大后缀,最大子段和 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N 500010;int n,m;int w[N];s…...
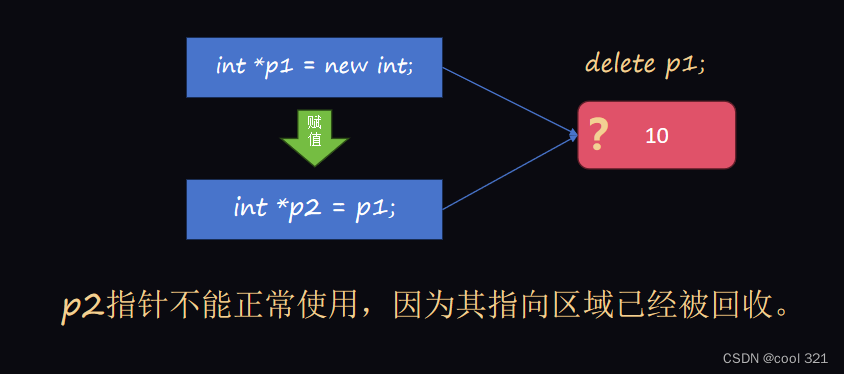
C++-指针
在C中,指针是至关重要的组成部分。它是C语言最强大的功能之一,也是最棘手的功能之一。 指针具有强大的能力,其本质是协助程序员完成内存的直接操纵。 指针:特定类型数据在内存中的存储地址,即内存地址。 指针变量的定…...
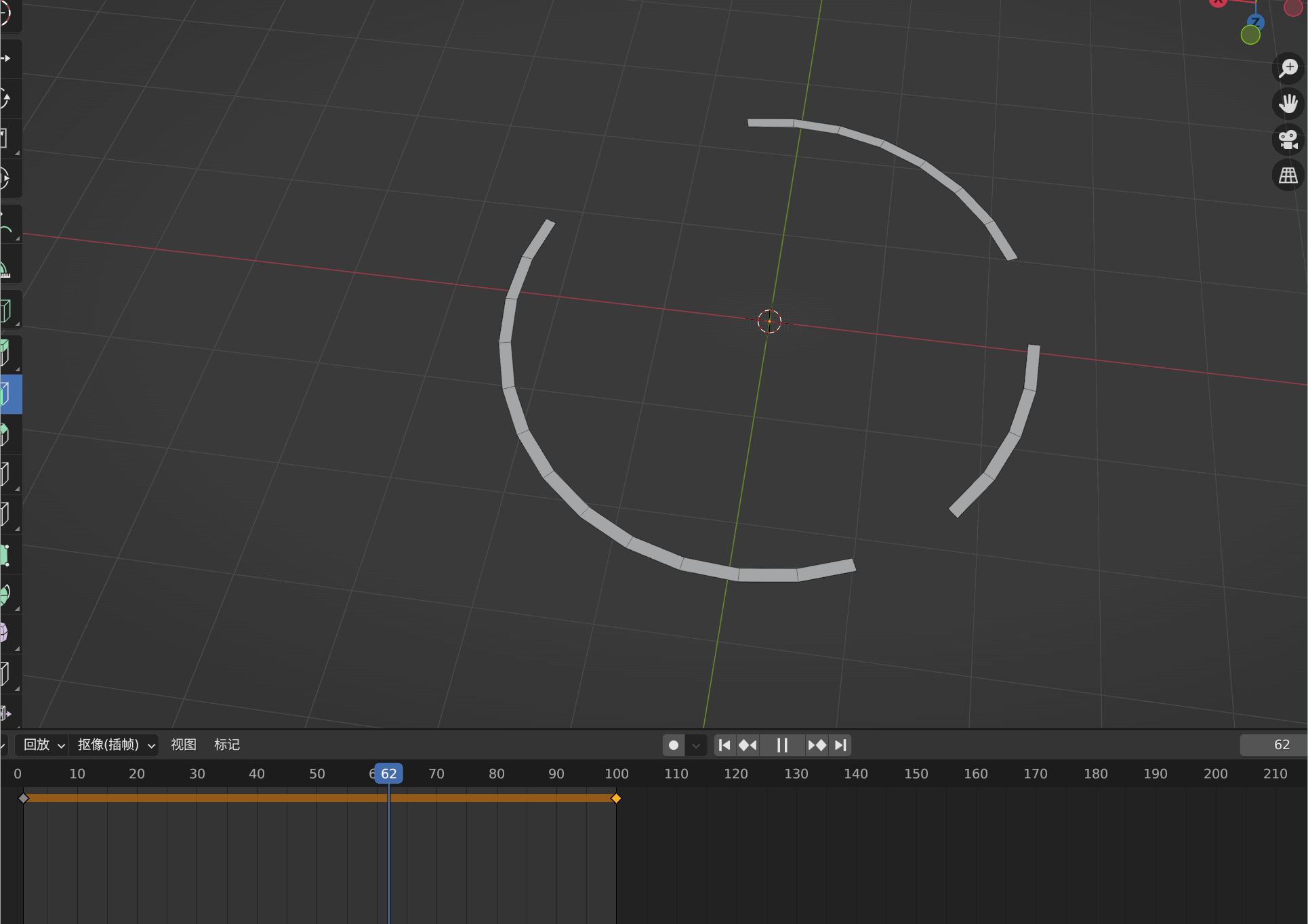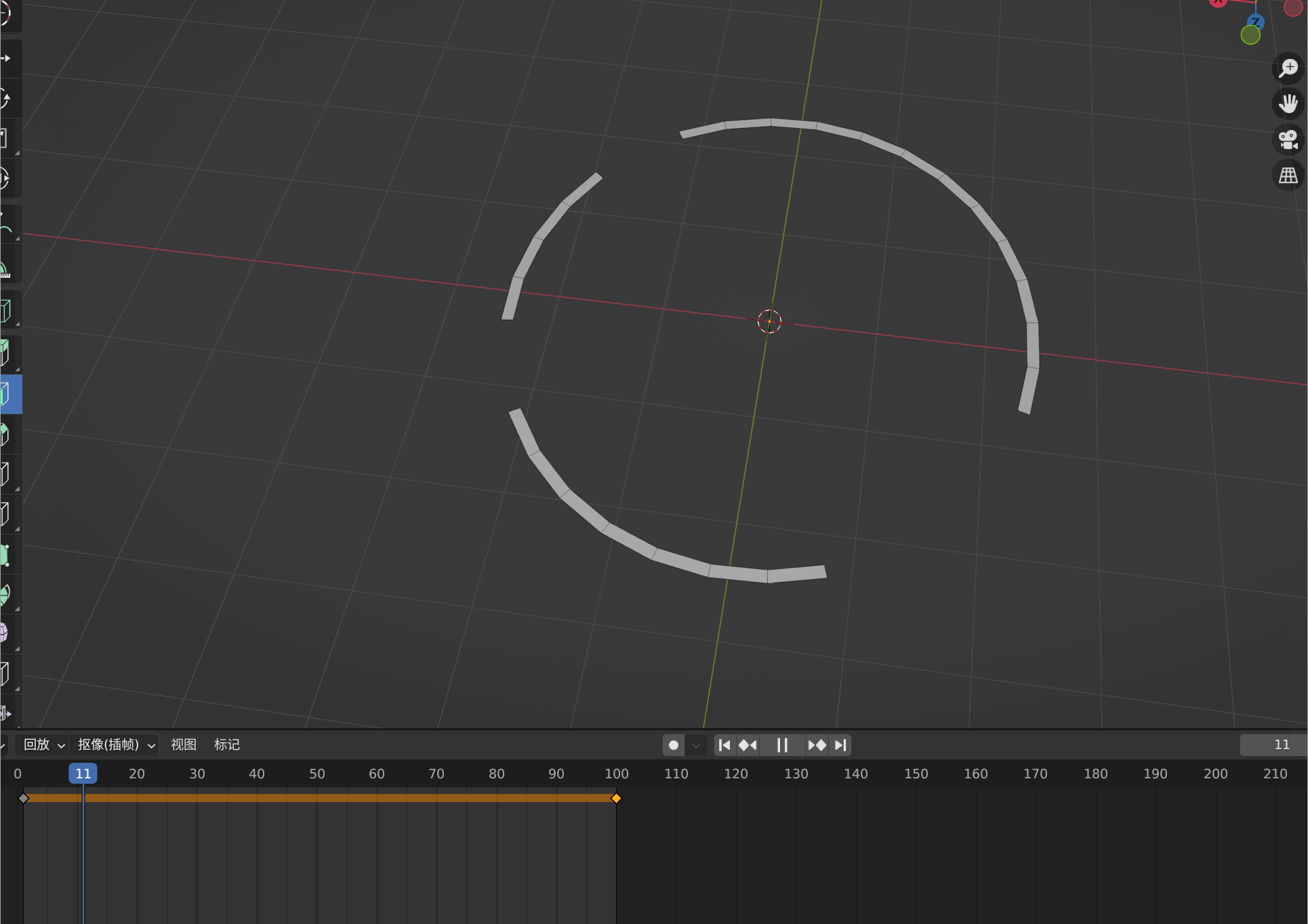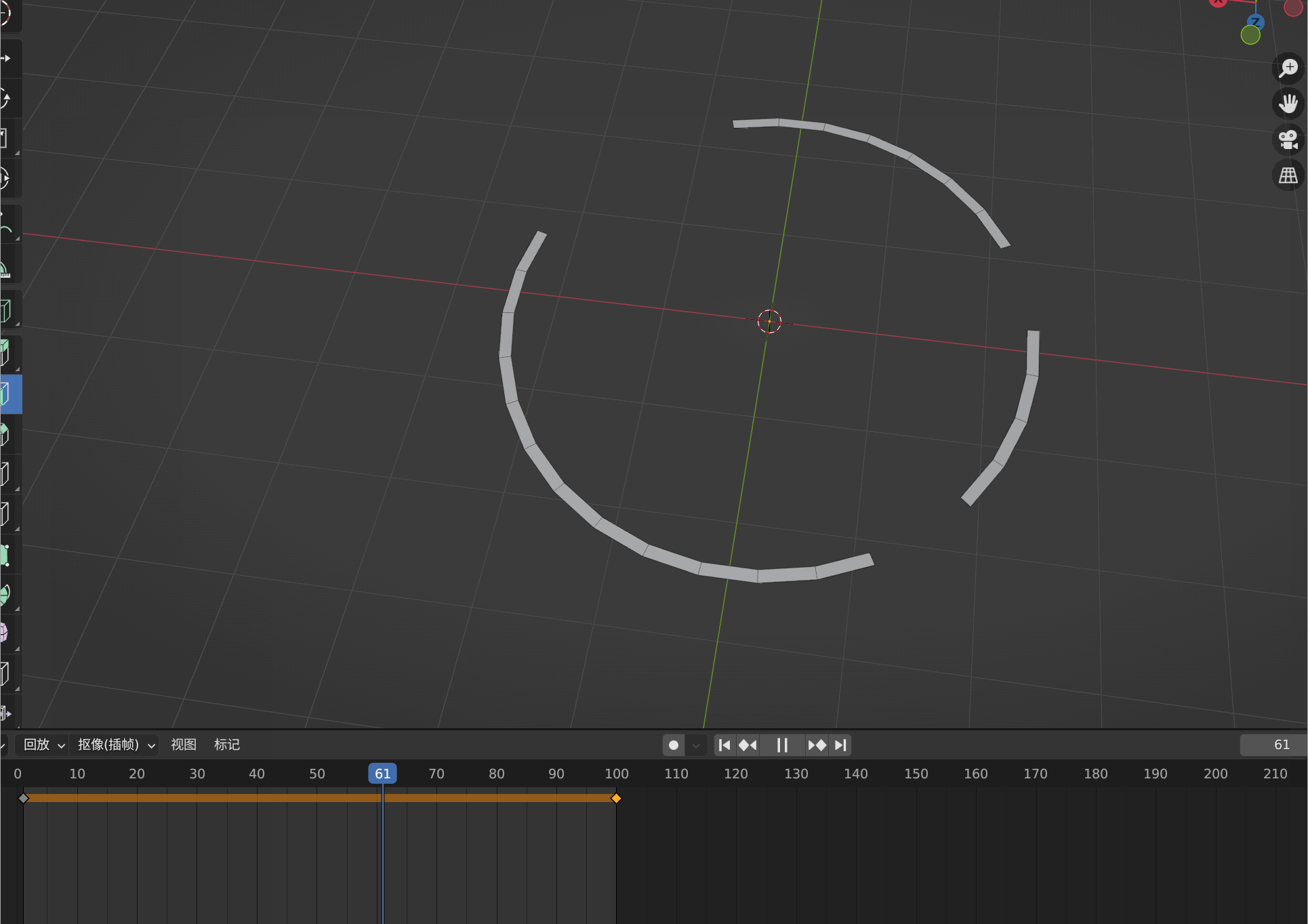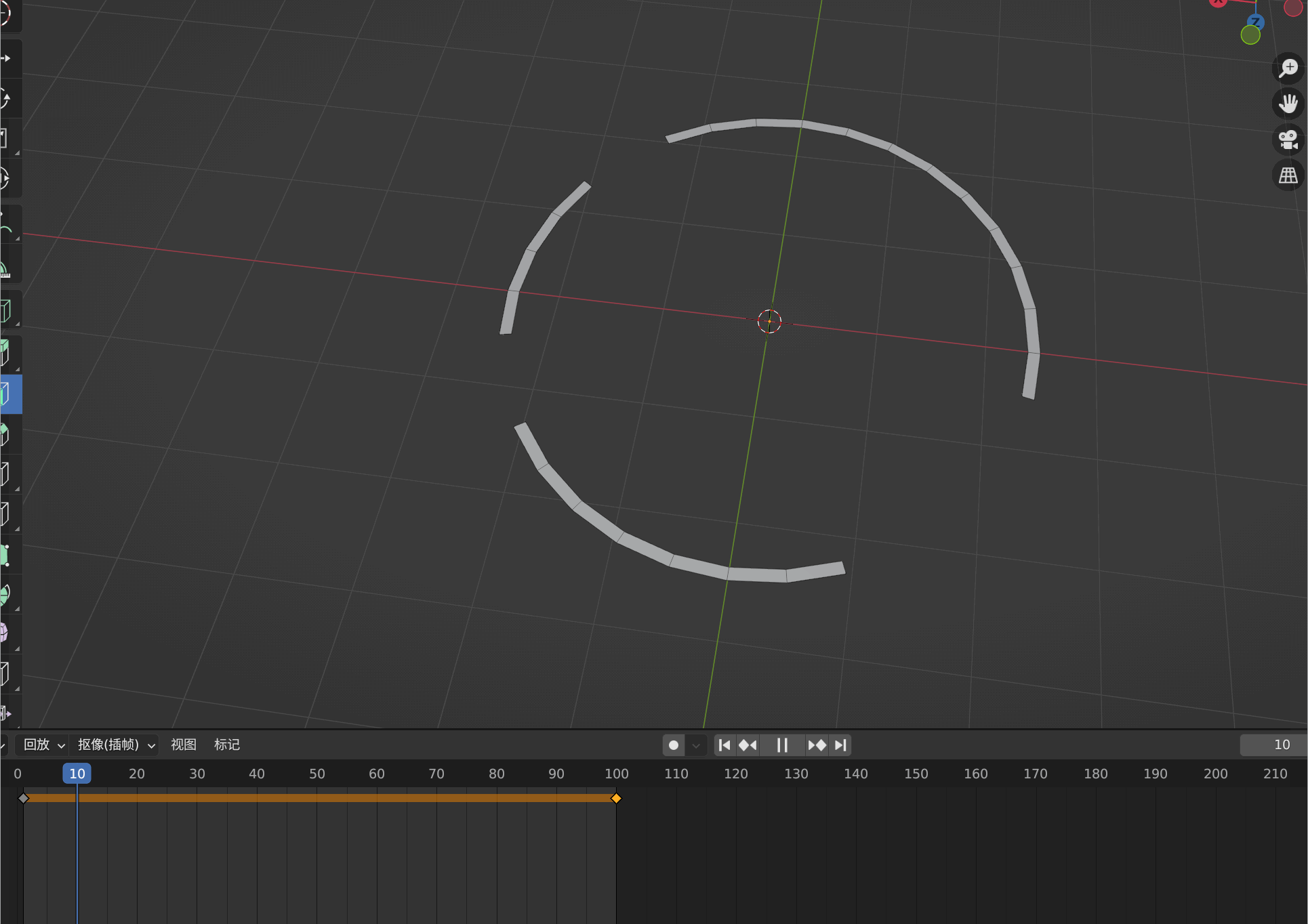
Three.js 研究:2、如何让动画线性运动
1、默认的动画含有加速度并非线性的 制作好的动画很明显是非线性的,这是一个运动环,为了让环运行线性进行如下设置。 2、设置动画成为线性动画...

z3-加法器实验
补码器加减法,运算方法简介 我们要知道什么是补码的加法,我们为什么要用补码的加法? 补码的加法其实就是将两个补码形式的二进制数字直接相加,处理的时候忽略超出固定位数的进位。补码的加法运算和无符号二进制数的加法操作一样&…...
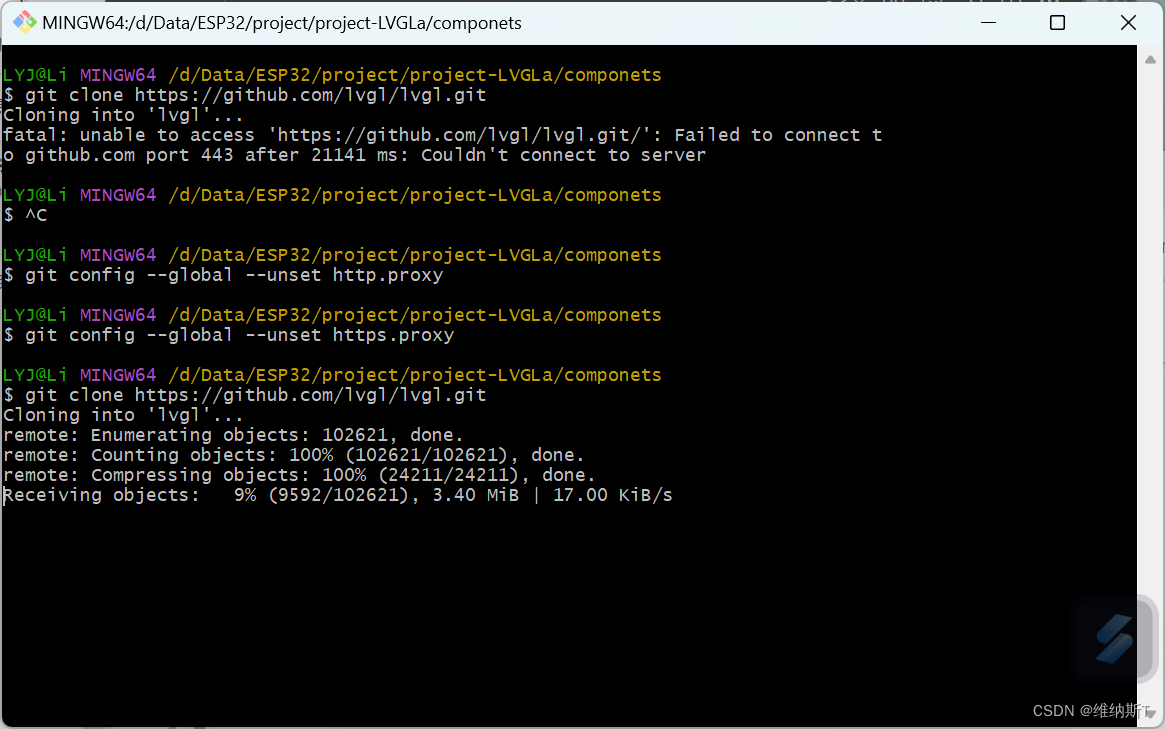
解决git克隆项目出现fatal无法访问git clone https://github.com/lvgl/lvgl.git
Windows 11系统 报错 $ git clone https://github.com/lvgl/lvgl.git Cloning into lvgl... fatal: unable to access https://github.com/lvgl/lvgl.git/: Failed to connect to github.com port 443 after 21141 ms: Couldnt connect to server 解决方法 git运行这两段代码…...

Vue中引入组件需要哪三步
在Vue中引入组件通常需要以下三步: 导入组件:首先,你需要在父组件中导入你想要使用的子组件。这通常是通过ES6的import语法完成的。 注册组件:接下来,你需要在父组件中注册这个子组件。这可以通过components选项完成&…...

到底该用英文括号还是中文括号?
这篇博客写的还挺详细的,不错。...

一个普通双非女生的秋招之路
大家好,我是小布丁。 先简单地做个自我介绍: 我今年本科毕业于某双非院校(属于那种没什么人听说过的小学校),学的是计算机专业,英语四级水平(没办法,六级确实没过)。我本…...

一个模型用了几层神经网络怎么算?
有权重参数的层算作一层,没有权重参数的就是参数不更新,不能称之为一层 有权重:卷积层、全连接层 没有权重的层:激活函数层、池化层 即数卷积层和全连接层的个数,就是这个模型用了几层神经网络。...

python获取cookie的方式
通过js获取cookie,避免反复登录操作。 经验证在JD上没有用,cookie应该无痕或者加密了,只能用单浏览器不关的模式来实现,但是代码留着,其他网站可能有用。 def cookie_set():driver webdriver.Chrome(optionschrome_…...
Nginx-狂神说
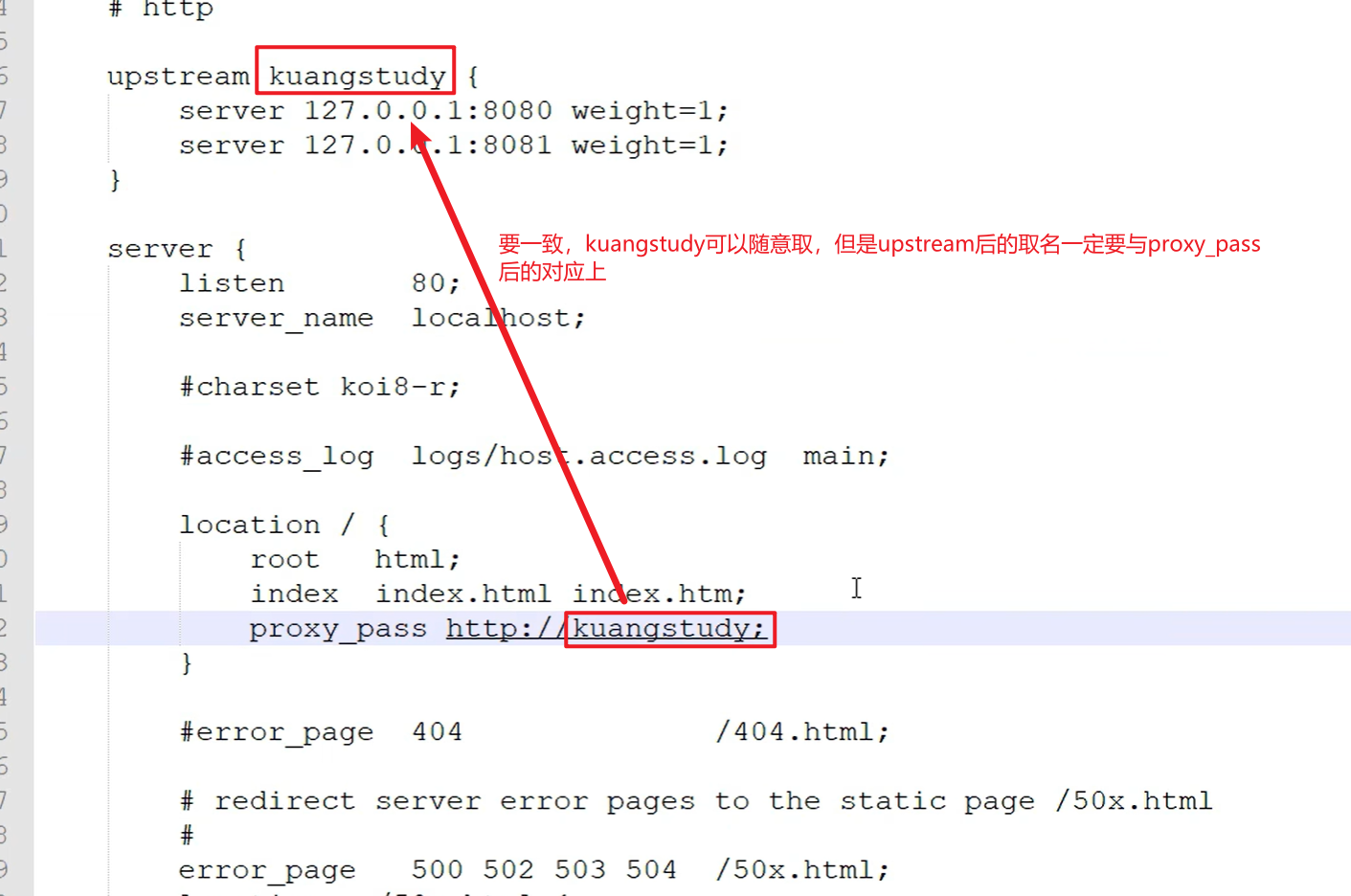
Nginx概述 公司产品出现瓶颈? 我们公司项目刚刚上线的时候,并发量小,用户使用的少,所以在低并发的情况下,一个jar包启动应用就够了,然后内部tomcat返回内容给用户。 但是慢慢的,使用我们平台…...
Python筑基之旅-运算符
目录 一、运算符 1、了解定义 2、理解意义 2-1、基本数据处理 2-2、条件判断 2-3、逻辑操作 2-4、赋值和更新 2-5、位操作 2-6、提高代码可读性 2-7、解决实际问题 2-8、学习其他编程语言的基础 3、探索方法 3-1、理解概念 3-2、练习基本运算 3-3、掌握优先级 …...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

2025 后端自学UNIAPP【项目实战:旅游项目】7、景点详情页面【完结】
1、获取景点详情的请求【my_api.js】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http(/login/getWXSessionKey, {code,avatar}); };//…...

SpringBoot+MySQL家政服务平台 设计开发
概述 基于SpringBootMySQL开发的家政服务平台完整项目,该系统实现了用户预约、服务管理、订单统计等核心功能,采用主流技术栈开发,代码规范且易于二次开发。 主要内容 系统功能架构 本系统采用前后端分离架构,前端提供用户交互…...
